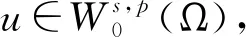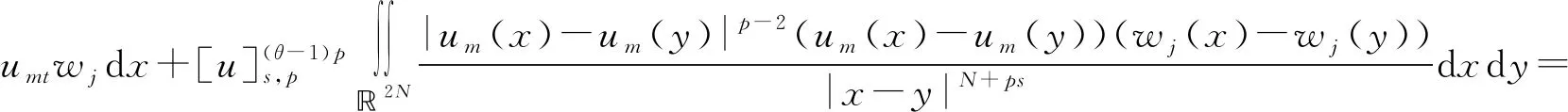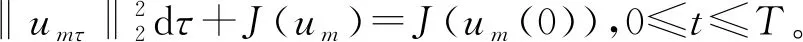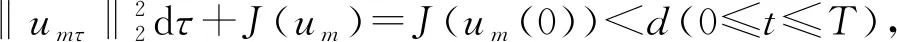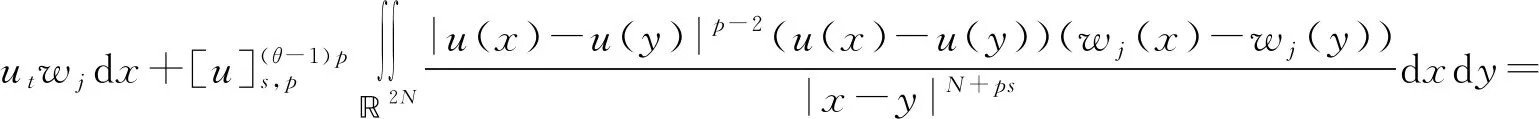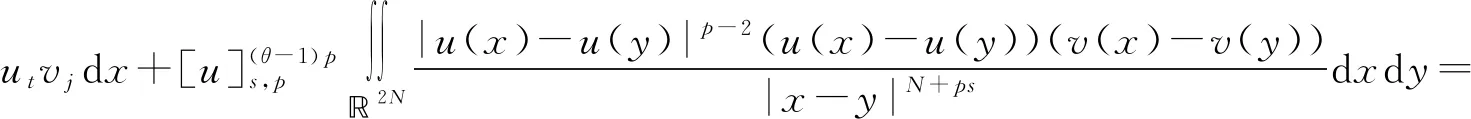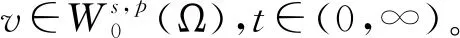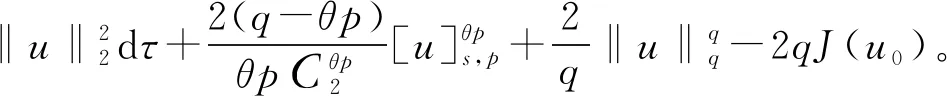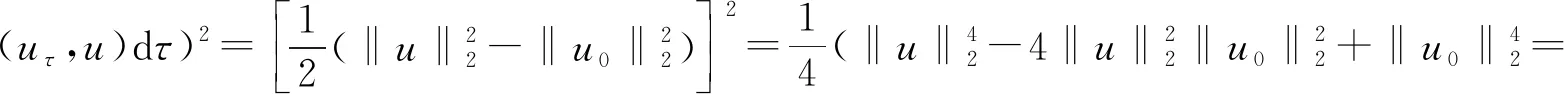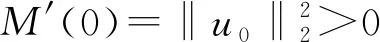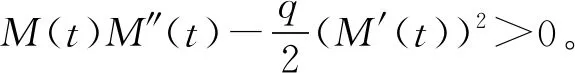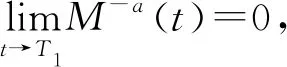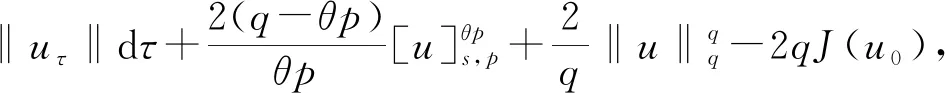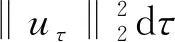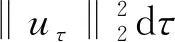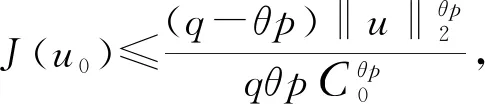一类分数阶拉普拉斯方程解的存在性与爆破性
邓启刚,石 鹏,曾福庚
(贵州民族大学 数据科学与信息工程学院,贵阳 550025)
0 引言
分数阶拉普拉斯方程相关问题的研究广泛来源于物理、化学、生物、气象、工程、地质等实际问题,近年来引起了学者们的广泛关注[1-3]。本研究考虑如下分数阶拉普拉斯方程
(1)
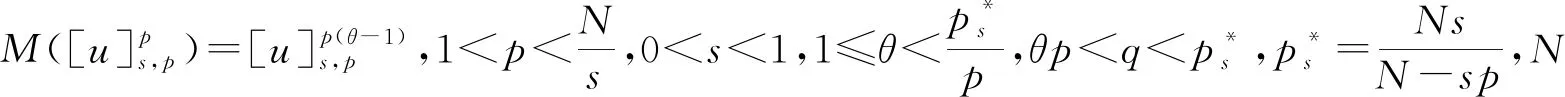

其中:Bε(x)表示一个在N上以x为圆心、ε为半径的球;[u]s,p是Gagliarodo半范数,满足
文献[4]研究了一类基尔霍夫型非线性抛物方程解的存在性和爆破性,文献[5]和文献[6]分别研究了一个带非局部积分-微分算子和带基尔霍夫扩散项的解的局部存在性、全局存在性和爆破性。文献[7]研究了一类带对数非线性项的分数阶拉普拉斯基尔霍夫方程的解的全局存在性和有限时间爆破性。在此基础上,本研究结合变分法理论讨论了上述式(1)在低初始能量J(u0) 首先定义能量泛函J(u)和Nehari泛函I(u)如下 (2) (3) 由式(2)和式(3)可知 (4) 然后定义位势井W和相应的集合V[8]如下 下面给出以下引理。 (ⅲ)J(λu)在0≤λ≤λ*时单调递增,在λ*≤λ≤∞时单调递减,λ=λ*在处取到最大值; (ⅳ)当0≤λ≤λ*时,I(λu)>0;当λ*≤λ≤∞时,I(λu)<0;在λ=λ*时,有I(λ*u)=0。 (ⅱ)由于 h′(λ)=-(q-θp)λq-θp-1ʃΩ|u|qln|u|dx-(q-θp)λq-θp-1lnλʃΩ|u|qdx-λq-θp-1ʃΩ|u|qdx= λq-θp-1-((q-θp)ʃΩ|u|qln|u|dx-(q-θp)lnλʃΩ|u|qdx-ʃΩ|u|qdx)。 假设存在一个λ1使得h′(λ1)=0,则 (ⅳ)因为 (ⅰ)若0<[u]s,p (ⅱ)若I(u)≤0,则[u]s,p≥r(σ)。 证明由I(u)的定义有 证明对于u∈,有以及I(u)=0,由d的定义和引理4的结论(ⅱ),有[u]s,p≥r(σ),由于 下面给出弱解、最大存在时间、有限时间爆破的定义,并给出与之相关的一些引理。 (ⅲ)对于0≤t≤T,有 (5) 定义2 (最大存在时间) 设u(t)是式(1)中方程的解,定义u(t)的最大存在时间如下: (ⅰ)如果u(t)存在时间为[0,∞),那么T=+∞; (ⅱ)如果存在t0∈(0,∞),使得u在0 证明通过弱解的定义有 引理7 若um(t)在(0,∞)×Ω上几乎处处收敛于u(t),则对于足够大m,有 ʃΩ|um|qln|um|dx-ʃΩ|u|qln|u|dx≤0。 证明由引理2可得 ʃΩ|um|qln|um|dx-ʃΩ|u|qln|u|dx≤ |ʃΩ|um|qln|um|+uum|um|q-2ln|um|-uum|um|q-2ln|um|-|u|qln|u|dx|= |ʃΩ(um-u)um|um|q-2ln|um|+u(um|um|q-2ln|um|-u|u|q-2ln|u|)dx|≤ 因此结论成立。 引理8 若在(0,∞)×Ω中um(t)→u(t)几乎处处成立,其中有um(t),u(t)∈W,则有 证明由于 因此结论成立。 本文主要讨论低初始能量J(u0) 其中:gjm(t)∈1[0,T)(0≤t≤T,j=1,2,…,m),同时满足故 ʃΩ|um|q-2umln|um|wjdx(0≤t≤T)。 对于j=1,2,…;djm=(um(0),wj)=gim(0)是一个常数,使得式(1)中方程在L2(Ω)上有意义,且 (7) 则对于足够大的m有 下证对于足够大的m和t0∈[0,T],有um(x,t)∈W。 假设um(x,t)∉W,则存在一个足够大的m和t0∈[0,T],使得有um(x,t)∈∂W,有I(um(t0))=0,J(um(t0))=d,因此有um(t0)∈。由于则有J(um(t0))≥d,与J(um(t0))=d矛盾。故当m→∞时,t∈[0,T]有um(x,t)∈W。 为了使m足够大,t∈[0,T],需满足: (9) (10) (11) 若um(t)∈W,且 ʃΩ|um(t)|q-2um(t)ln|um(t)|dx≤-ʃΩ(|um(t)≤1|)|um(t)|q-1ln|um|(t)dx+ ʃΩ(|um(t)>1|)|um(t)|q-1ln|um|(t)dx≤ 则在L∞(0,∞;L1(Ω))中|uv(t)|q-2vv(t)ln(vv(t))→|u|p-2uln|u|,在L2(0,∞;L1(Ω))中|uv(t)|q-2uv(t)ln(uv(t))→|u|p-2uln|u|。 M″(t)=2(u(t),u(t))=-2I(u), (12) (13) (14) 由式(13)、式(14)和施瓦兹不等式,可得 现在讨论两种情形: (ⅰ)若J(u0)≤0,那么有 (ii)若0 由施瓦兹不等式,有1预备知识

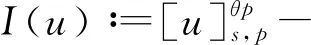
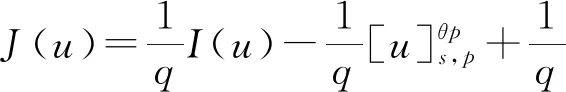


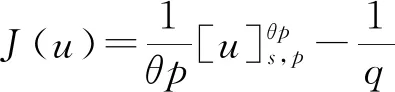
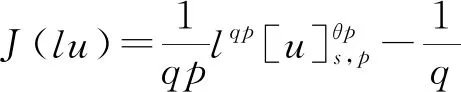


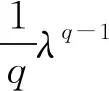
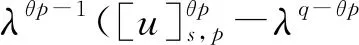
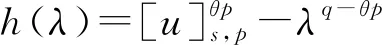
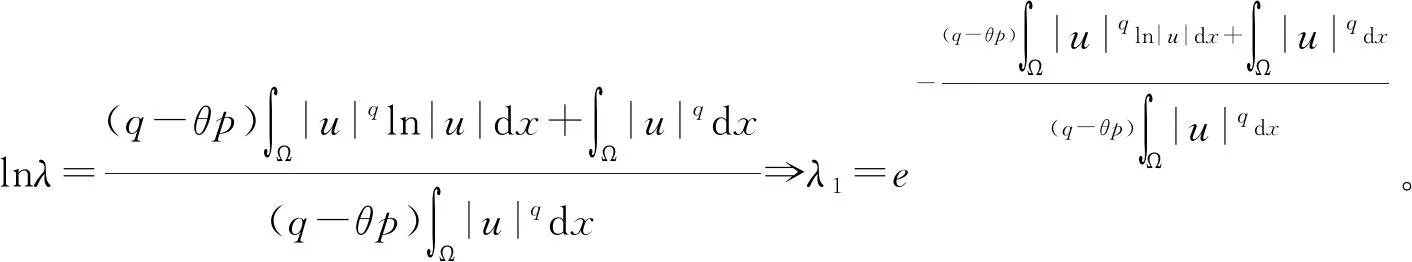
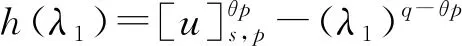
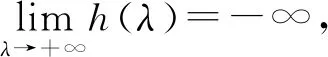
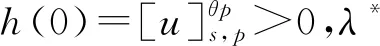

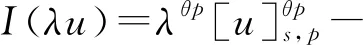
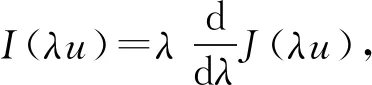



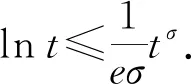
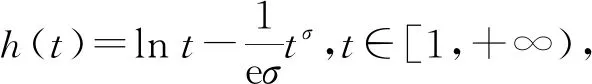

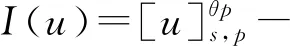
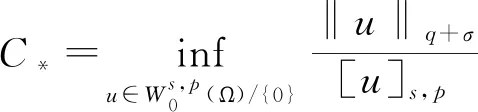

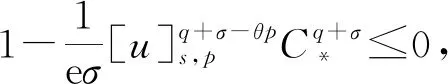
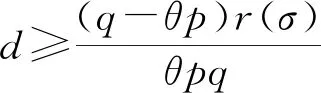

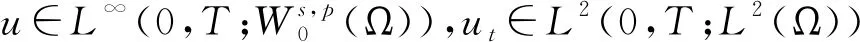
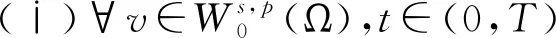
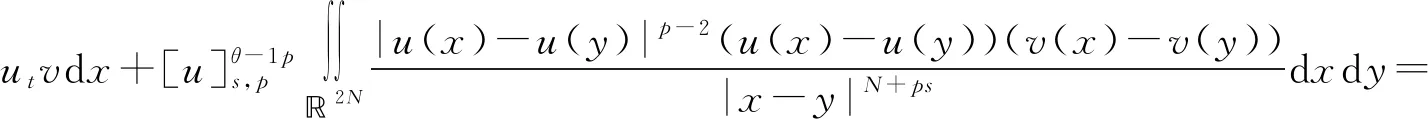
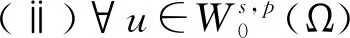
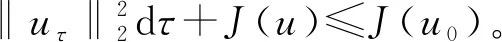
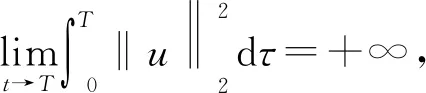
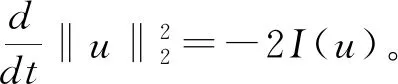
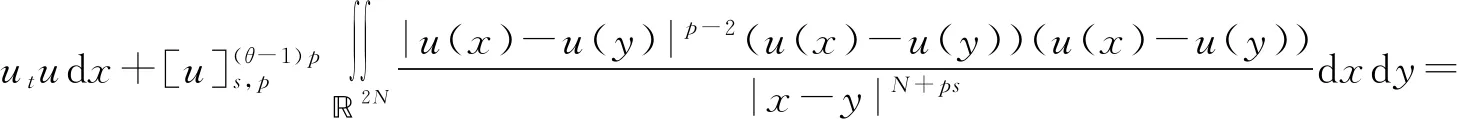
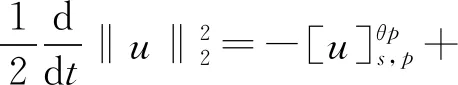

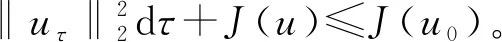
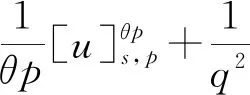


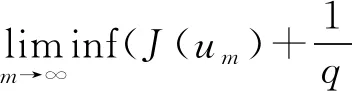
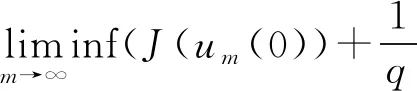

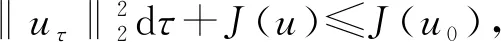
2 主要结果和证明