基于改进三阶半离散方法的铣削颤振稳定性预测*
马 耀,汪振华,卢跃峰,章 波
(南京理工大学机械工程学院,南京 210094)
0 引言
对于经典再生型颤振的稳定性预测一直是机械加工领域的重要课题,众多学者对其进行研究,提出的预测方法主要分为数值法和解析法两大类[1]。
在解析法中,文献[2]提出经典半离散方法,之后对半离散法进行改进,使用一次多项式插值近似时滞项,将零阶半离散方法发展至一阶半离散方法[3]。由于半离散法采用多个等距时间点来离散刀齿通过周期,并且可以考虑一种或多种效应,因而在加工领域已有诸多应用。文献[4]基于半离散法,提出快速获得的变螺旋铣刀的稳定性叶瓣图方法。但是,在半离散法的数值计算过程中,需要计算大量的指数矩阵和矩阵序列,这是因为在扫描切削参数空间时必须在内部循环中对其进行更新,这会导致半离散法计算效率的损失。
在半离散基础上,文献[5]提出全离散方法,为了减少内部循环时指数矩阵的计算次数,采用类似哈密顿正则替换方法,将空间形式的方程分为常数项和时变项,从而只需在主轴转速循环内计算常数项指数矩阵项,减少计算过程中指数矩阵的计算次数。文献[6]使用全离散法获得超声附和铣削系统的稳定性叶瓣图。文献[7]使用全离散法研究铣刀磨损对铣削稳定域和表面形位误差的影响。文献[8]在全离散基础上,通过精细时间积分方法改良计算时间损失,并且提出使用黄金搜索法改良顺序扫掠寻找关键切深的计算结构。
在数值计算方面,文献[9]基于半离散方法在处理指数矩阵时需要消耗大量的计算时间,提出一种用于铣削稳定性预测的完全离散化方法,离散化了延迟微分方程的所有部分,包括延迟项,时域项和参数矩阵。由于采用直接积分的方案,避免了指数矩阵的计算。文献[10]提出使用二分查找方法寻找关键轴向切深的计算框架,提出一种基于龙格库塔的完全离散化方法。文献[11]使用增强型完全离散法对球头铣刀五轴切削稳定域预测。
综上所述,由于半离散法较低的计算效率,高阶半离散法相较于低阶方法更高的计算精度与递归搜索关键切深的高效计算框架,本文提出使用三阶牛顿插值多项式来近似时间延迟项,采用二分查找法寻找关键切深,同时使用精细时间积分算法[12]的改进三阶半离散法。
1 改进三阶半离散法
考虑单自由度动力学模型,将其转化为状态空间形式[2]可得:

(1)
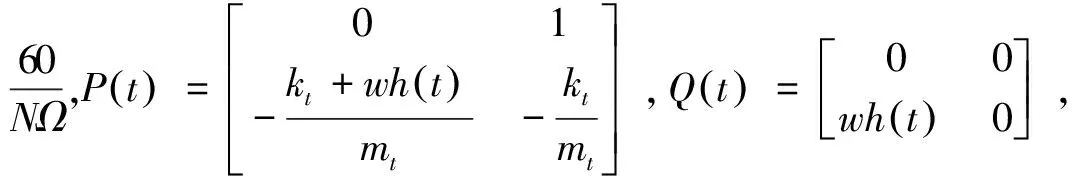
φj(t) 为当前切削角度,表示为:
(2)
其中,j为当前切削刀齿数,j=1,2,···,N,N为刀具总齿数。
g(φj(t)) 为窗函数,表示为:

(3)
式中,φst和φex分别表示为切入角和切出角,与加工方式有关,表示为:

(4)
其中,a/R为浸入比,为径向切深和刀具半径的比值。
对于式(1)的响应可以表达为如下直接积分表达式:
(5)
对式(5)中的Q(kτ+τ-s)和X(kτ+τ-s-T)两项进行插值处理,其中周期系数矩阵Q(kτ+τ-s)使用两端项Qk+1=Q(kτ+τ),Qk=Q(kτ)进行线性插值,得:
(6)
对时滞项X(kτ+τ-s-T)进行三阶牛顿多项式插值,得:
X(kτ+τ-s-T)≈aXk+3-m+bXk+2-m+cXk+1-m+dXk-m
(7)

式中,Xk+1=X(kτ+τ),Xk-m=X(kτ-mτ),Xk+1-m=X(kτ+τ-mτ),Xk+2-m=X(kτ+2τ-mτ),Xk+3-m=X(kτ+3τ-mτ)。
将式(6)和式(7)带入式(5)得到:
Xk+1=F0Xk+Fm-3Xk+3-m+Fm-2Xk+2-m+Fm-1Xk+1-m+FmXk-m
(8)
其中,F0=Φ0
(9)
Fm-3=Qk+1(L5-L1)+QkL1
(10)
Fm-2=Qk+1(L6-L2)+QkL2
(11)
Fm-1=Qk+1(L7-L3)+QkL3
(12)
Fm=Qk+1(L8-L4)+QkL4
(13)
并且,
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
指数矩阵Φ1~Φ5由精细时间积分法计算[12]。
由式(8)构造离散映射:
yk+1=Akyk
(22)
式中,yk=col(Xk,Xk-1,···,Xk+1-m,Xk-m)
(23)
Ak为序列矩阵,表示为:
(24)
而后,一个周期上转移矩阵Θ可以由矩阵序列Ak(k=0,1,···,m-1)表达出来,即:
ym=Θy0
(25)
其中,Θ=Am-1Am-2···A1A0。
(26)
最后根据Floquet理论获得稳定极限曲线,若转移矩阵特征值等于1,则系统临界稳定。采用二分查找法寻找关键切深,图1为算法流程图。

图1 三阶半离散方法流程图
2 算法收敛率分析
使用MATLAB进行仿真,参数选择与文献[13]中相同,在表1中列出。加工方式为顺铣,径向切削深度与刀具直径之比a/D=1,主轴速度Ω=5000 rpm,4个轴向切削深度ap=0.1,0.4,0.7和1 mm。在图2中,y轴表示精确关键特征值μ0和近似关键特征值μ之间的偏差:其中,μ0由一阶半离散法确定,离散参数选择m= 1000。可以证明,如果m足够大,采用4种方法取得的||μ|-|μ0||值都将接近0。因此,如果一种方法具有更快的收敛速度,则||μ|-|μ0||的值将更快地接近0。
在相同的切削条件下,0th-SDM,1st-SDM, 2nd-SDM和3rd-SDM的收敛曲线在图2中显示。从图中可以看出,与低阶的半离散法相比,三阶半离散法具有更快的收敛速度。例如,如图2b所示,在m= 50时,3rd-SDM获得的||μ|-|μ0||值为5×10-4。而0th-SDM,1st-SDM和2nd-SDM所获得的误差值分别是32×10-3,18×10-3和7×10-3,都大大超过5×10-4。不难发现,本文提出的3rd-SDM相比于0th-SDM,1st-SDM,2nd-SDM具有更快的收敛速度。

(a) ap=0.1 mm,|μ0|=0.736 763 3(稳定)
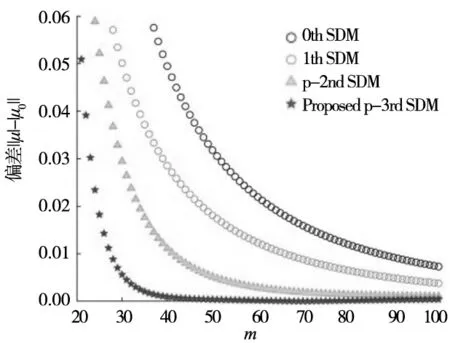
(b) ap=0.4 mm,|μ0|=0.991 715 5(稳定)
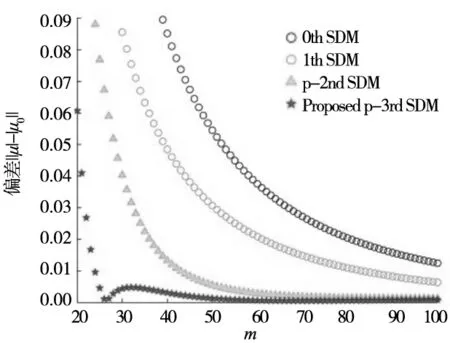
(c) ap=0.7 mm,|μ|=1.219 689 0(稳定)
3 有效性验证
为了清楚的比较所提出半离散方法的计算效率和精度,传统的零阶半离散法和一阶半离散法将其表示为0th-SDM和1st-SDM,而二阶半离散法采用精细时间积分法,记为p-2nd-SDM,本文提出的改进三阶半离散法记为I-3rd-SDM。为了比较所提出I-3rd-SDM与其它半离散法的计算效率,与文献[13]采用的方法相似,在高速铣削加工条件下,从计算效率和铣削稳定性预测的准确性方面验证了所提出算法的有效性。图3显示了使用不同半离散法获得的稳定性叶瓣图与相应的计算时间。为了进行清楚的比较,由1st-SDM确定参考稳定性叶瓣图,取m= 300,并用红色标记为精确的参考稳定边界,蓝色线条为相应半离散法求出稳定边界曲线。铣削动力学系统的模态参数如表2所示。加工参数为顺铣,浸入比a/D=1。

表1 模态和铣削参数
图3给出了高主轴速度时具有不同离散参数m=20,30和40时0th-SDM,1st-SDM,p-2nd-SDM与I-3rd-SDM获得的稳定性叶瓣和所耗费的计算时间。所有算法均位于Ω∈[5×103,10×103] rpm和ap∈[0,4] mm进行计算,stx×sty=200×100。从图3中可以看出,由于采用PTI算法,花费的计算时间更少。例如,在m= 30时,0th-SDM和1st-SDM的计算时间分别为144 s和93 s。p-2nd-SDM的计算时间为46 s,相比于0th-SDM和1st-SDM的计算时间分别减少68%和50%。更显著的时间减少发生在p-2nd-SDM和I-3rd-SDM之间,由于I-3rd-SDM采用二分查找的计算框架,只需要花费6 s,这意味着I-3rd-SDM具有更高的计算效率。
在计算精度方面,如图3所示,与低阶方法相比, I-3rd-SDM获得的稳定性叶瓣图与参考稳定性边界具有更好的一致性。例如,在m=30时,0th-SDM和1st-SDM的稳定性凸角与参考稳定性边界有明显的偏差。尽管p-2nd-SDM进一步减小了偏差,但与参考稳定性边界中间区域和顶部区域之间仍然存在明显的差异。当使用I-3rd-SDM时,虽然存在PTI算法带来的计算精度下降,但是稳定性波瓣中间部分几乎与参考稳定性边界重合,而顶部区域也只有较小的偏差。这进一步表明,与低阶SDM相比,本文提出的I-3rd-SDM具有更高的计算精度。




图3 高速铣削时0th-SDM、1st-SDM、P-2nd-SDM与I-3rd-SDM的计算精度比较
4 结论
本文基于三阶牛顿插值多项式和精细时间积分法,结合二分查找法寻找关键切深,提出一种用于铣削稳定性预测的改进三阶半离散方法,可以得到如下结论:
(1)对于考虑再生效应的铣削动力学等式,通过柯西转换转变为状态空间的微分时滞方程,对时滞采用三阶牛顿插值多项近似,获得各个等距时间点的矩阵序列,从而求得传递矩阵特征值并应用Floquet理论,获得稳定性叶瓣图。
(2)在收敛性、有效性等方面将改进三阶半离散法与低阶半离散法进行了比较。结果表明,三阶半离散法的收敛速度更高。在算法有效性方面,三阶半离散法兼具计算精度和计算效率。
(3)仿真的结果也表明,采用二分查找法框架获得稳定性极限曲线的效率将产生巨大的提高,并且该方法也适用于低阶的半离散法中使用,将会进一步拓宽半离散法在实际加工中的应用。

