践行数学美育 构建审美课堂*
江苏省无锡市第一中学 (214031) 黄 荣
《普通高中数学课程标准(2017年版)》指出,学会审美不仅可以陶冶情操,而且有助于改善思维品质.数学课堂教学,要促使学生对美的感受从感性走向理性,不断提升审美情趣和审美能力,同时增强形象思维能力和理性思维能力[1].从课堂教学现状来看,数学美育未能得到应有的重视,数学的审美价值未能得到充分的挖掘,数学课堂还远未达到美观、美好、美妙的境界[2].
一、聚焦课堂教学,构建审美课堂
数学有其独特的审美价值和魅力.“哪里有数,哪里就有美”,数学之美可谓无处不在,数学家能在数学中领略到数学美的神韵.但受限于数学知识、审美情趣和审美能力,学生眼中的数学却往往是枯燥乏味的.正如罗素所言“数学是一种至高的美,一种冷而严肃的美”,数学美不同于自然美和艺术美,需要在教师引领下借助数学思维方能品味.
践行数学美育要警惕几种倾向.其一,停留于“什么是数学美”、“体现何种数学美”的理念层次,这种做法纠缠于美学概念,浮于简单化和表面化,违背了数学美育的初衷.其二,停留于感性层次的数学审美,例如呈现美妙的画面、唯美的公式、对称的定理,这是必要的,但又远远不够,还需引导上升到理性层面的数学审美.其三,超越学生的审美认知,展示学生所不能领略的美,以致适得其反,数学美育应当循序渐进,从感性走向理性,从欣赏走向创造.
鉴于上述认识,笔者以为,数学美育应该聚焦课堂,让数学之美自然蕴含于课堂教学,实现数学知识、方法、思维、文化、审美的和谐统一,让学生在潜移默化中欣赏、深化、创造、拓展数学之美.
二、践行数学美育的教学路径
1.创设美观情境,欣赏数学之美
爱美之心,人皆有之,数学美育要抓住这种与生俱来的心向,挖掘课程的内隐性资源,创设美观的学习情境,引导学生欣赏数学之美.



图1
2.把握美好本质,深化数学之美
数学之美,美在内涵,惟有以数学思维为体,审美思维为翼,方能把握数学的美好本质,深化对数学之美的认识.



本题的求解,借助对数把数列递推关系中的乘、除关系转化为加、减关系,巧妙构造出等比数列,一举破题.如果进一步挖掘,其实对数概念中蕴含着对应思想,设计教学时可以对应思想为主线,串联指对数、三角、数列、线性规划、统计等不同内容,纵横联系,有助于学生系统把握方法本质.总之,只凭美感与直觉并不足以深刻体悟数学之美,还需以理性思维追根溯源,如此方能把握数学本质,体悟到数学的至真至善至美.
3.探索美妙方法,创造数学之美
数学教学不能停留于欣赏数学之美的层次,还要善于激活思维,引导学生探索数学之美,亲历创造数学之美的过程.
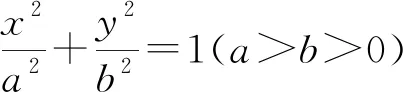


图2


解法一解决此题显得计算繁杂.有没有简洁优美的解法?学生经过探索,挖掘几何性质,提出了解法二.还有学生根据角平分线定理提出解法三,与解法二有异曲同工之妙.总之,解题教学要善于引导学生优化解题思维,提出更多的美妙解法.
4.跨越美育疆界,拓展数学之美
数学美育需要全方位渗透,借助“文献阅读与数学写作”,引导学生跨越课堂内外与学科疆界,从而将数学美的浸润拓展到课堂之外.
以对数函数的教学为例.当笔者讲授到“以e为底的对数称为自然常数,e是无理数,约等于2.71828”.学生提出,e究竟是什么,又为何冠名为“自然”二字等问题.笔者顺势布置文献阅读任务,指导学生查阅文献,搜集素材.阅读汇报课教学环节如下:


图4
环节三:小结.笔者以指数式(1+0.01)365≈37.78343433,(1-0.01)365≈0.025517964结尾,激励学生珍惜青春年华,不断探寻数学的至真至善至美.
总之,新时代呼吁绚丽多姿的审美课堂,广大数学教师要多角度、全方位的挖掘数学之美,寓美于教,以美启智,培养学生的审美思维和理性思维,提升学生的数学素养.当然,要实施具有较高品位的数学美育并不容易,需要教师不断提高自身的数学素养,做到多研读、多思考、多实践.

