一类时滞分数阶计算机病毒模型的Hopf分岔研究
高燕鑫, 石剑平
(昆明理工大学 理学院, 云南 昆明 650500)
现实问题里很多系统的变化过程不仅依赖当前时刻的状态,还依赖于过去某个时刻或某段时刻的状态,这种特性称为时滞。由于物质和能量在变化的时候往往不能瞬间传递,时滞发生在几乎所有类型的自然和社会系统中[1-2]。计算机病毒模型[3-4]是一种以时间为状态变量的微分方程系统,引入时滞来描述和分析其动力学特征早就成为研究者的共识[5-6],并取得了很多有价值的成果。
近几十年,分数阶微积分[7]在众多科学与工程领域得到了成功的应用。由于能够描述存在于医学、物理学、生物学、工程应用等系统中所固有的记忆和遗传特性[8-10],相比整数阶微积分,分数阶微积分为系统性能的描述提供了更为丰富的自由度,有助于更加科学有效地研究系统的稳定性以及分岔等动力学性质[11-13]。本文基于前人的研究结果,对一类时滞计算机病毒传播模型[14]引入分数阶进行描述,通过增加系统的时滞项,获得一个分数阶时滞计算机病毒模型。并以时滞项作为控制参数,研究系统在正平衡点处的稳定性以及出现Hopf分岔的条件。
1 模型描述
由于状态变量在分数阶的情况下可以考虑不同的变化率,因此本文对文献[14]研究的一类时滞计算机病毒传播模型引入不同的分数阶,并对最后一个方程也加入时滞项,获得下述的改进系统模型
(1)

研究分数阶微分方程系统的稳定性和分岔问题,目前并没有完善的理论体系。文献[15]利用线性化近似系统在平衡点处的稳定性来研究原系统的稳定性和分岔问题,并给出了明确的定义,说明系统时滞项τ满足一定的条件,在平衡点处会出现Hopf分岔。此研究思想的核心是以时滞τ作为控制参数分析分数阶系统平衡点的稳定性。
定义1[15]对于以下n维时滞分数阶系统
(2)
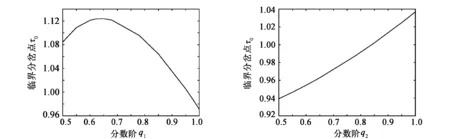
0 注1:定义1中,条件(1)说明当时滞τ=0时,分数阶微分方程系统(2)在0 下文将根据这个定义,结合系统(1)研究其在正平衡点处的稳定性和Hopf分岔。 计算系统(1)的平衡点为 由于系统参数均大于零,E0是系统(2)的一个无病平衡点。但是当I(t)=0时,系统中已没有感染节点。本文主要研究存在感染节点的平衡状态下系统的稳定性,为此,需要考虑系统参数满足什么条件时,E1为正平衡点。由于模型(1)的参数较多,下面通过引入基本再生数来分析系统存在正平衡点的条件。 基本再生数是传染病模型的重要概念,描述已感染的病人在平均患病时间内感染易感染者的人数,记作R0。在计算机病毒传播模型中,可用基本再生数描述病毒传播的情况:若R0>1时,病毒侵入易感节点;若R0<1,经过一定的时间,病毒将被彻底清除。下面采用再生矩阵方法[16]计算 。 系统(1)对应的整数阶系统为 (3) 令U(t)=(I(t),S(t),R(t))T,则当τ=0时,(3)式可以表示为 (4) 其中 f(U(t))描述新感染个体的比率,ν(U(t))则表示转移比率。 计算f(U(t))和ν(U(t))在无病平衡点E0处的Jacobian矩阵 (5) 由文献[16]可知再生矩阵为FV-1,基本再生数R0是再生矩阵的谱半径ρ(FV-1),即再生矩阵FV-1的特征值λ0模的最大值。由(5)式可得 其中I是单位矩阵。 故系统(3)的基本再生数为 (6) 定理1 若R0>1,则系统(1)存在唯一的正平衡点E*=E1,若R0≤1,则系统(1)不存在正平衡点。 证明由(6)式,系统(1)的平衡点E1的各分量可写为 (7) 显然恒有S*>0,当R0>1时,I*>0,R*>0,即系统(1)存在唯一的正平衡点E*=E1(S*,I*,R*),当R0≤1时,有I*≤0,即系统不存在正平衡点。 在本节中,以时滞作为参数分析系统(1)发生Hopf分岔的条件。首先,在正平衡点E*做变换 x(t)=S(t)-S*,y(t)=I(t)-I*,z(t)=R(t)-R*, 则系统(1)可以转化为 (8) 系统(8)在原点处的线性化系统为 (9) 其中 a11=-(μ+k), a31=k,a12=-βS*, a32=γ,a13=-βI*, a33=-μ。a21=βI*, (10) 下面根据定义1,分析系统(1)在正平衡点发生Hopf分岔的条件。 条件1τ=0时,线性化系统(9)系数矩阵的特征根分析。 当τ=0时,系统(9)的系数矩阵对应的特征方程为 λ3-(a11+a13+a33)λ2+(a11a33+a13a33-a12a21)λ+a12a21a33=0, (11) 计算得 为了分析τ=0时(11)式的根λj(j=1,2,3)的取值情况,不妨作如下假设: (H1) -(a11+a13+a33) ·(a11a33+a13a33-a12a21) -a12a21a33>0。 引理1 如果假设(H1)成立,那么线性化系统(9)系数矩阵的所有特征根λj(j=1,2,3)均具有负实部。 条件2τ>0时系统(1)产生Hopf分岔的临界值分析。 对系统(9)的两侧分别作Laplace变换[17],得 (12) 其中 Δ(s)被看作系统(9)的特征矩阵,其中系数a11、a12、a13、a21、a31、a32、a33由(10)式决定,故系统(9)的特征方程为 P1(s)+P2(s)·e-sτ=0, (13) 其中 P1(s)=sq1+q2+q3-a11sq2+q3-a33sq1+q2+a11a33sq2, P2(s)=a13a33sq2-a13sq2+q3-a12a21sq3+a12a21a33。 由定义1可知,系统(1)发生Hopf分岔的条件之一是当τ=τ0时,线性化系统(9)的特征方程有一对纯虚根。不妨假设s=ωi=ω(cos(π/2)+isin(π/2))(ω>0,i为虚数单位)是(13)式的根,代入分离实部和虚部并化简,将cos(ωτ)和sin(ωτ)看作未知项,可得到以下方程组 (14) 其中A2和B2分别是(13)式实部和虚部经过整理后,cos(ωτ)和sin(ωτ)项的系数部分,A1和B1则是剩余的常数项。 求解方程组(14)可得 (15) 当系统(1)中的所有参数给定时,联立公式sin2(ωτ)+cos2(ωτ)=1,可以计算出ω的值。代入(15)式求解得 根据时滞的实际意义,主要关注出现Hopf分岔的最小正值,因此,将该分岔点描述为 (17) 条件3 横截条件分析。 根据隐函数求导法则,在(13)式两边分别对τ求导,可得到 (18) 其中 通过计算,可以得到 其中Mj和Nj(j=1,2)分别是M(s)、N(s)的实部和虚部。其解析过程略。 给出以下假设: (H2)M1N1+M2N2>0, 则得到横截条件成立的引理。 引理2 若假设(H2)成立,令s(τ)=γ(τ)+iω(τ)是(13)式在τ=τ0附近满足γ(τj)=0,ω(τj)=ω0的根,下面的横截条件成立 (19) 综上所述,由定义1得到以下结论: 定理2 假设(H1)和(H2)成立,给定参数组(p,b,μ,β,γ,k),则当τ=τ0时,系统(1)在正平衡点E*处产生Hopf分岔,τ0为(17)式定义的时滞临界点。 在本节中,基于文献[18]介绍的Adama-Bashforth-Moulton预估-校正方法,给出数值实例来验证前述理论分析方法的可行性和结果的正确性,其中步长取h=0.01。 为了更具有对比性,模拟所用的系统参数均来自文献[14],p=0.9,b=1,β=0.4,γ=0.1,μ=0.1,k=0.1,则系统(1)为 (20) 为了验证此结果的正确性,本文模拟了两种情况:选取初值为(0.2,4.5,5.4),分数阶为q1=0.92,q2=0.95,q3=0.98,取时滞τ=0.98<τ0=1.024 8时,系统(20)在平衡点(S*,I*,R*)=(0.5,4.0,5.5)处是渐近稳定的(见图1)。此结果说明随着时间的推移,易感节点、感染节点和恢复节点均趋于稳定值,虽然系统仍然存在感染节点,但是数量稳定,有利于采取恰当措施对系统进行干预,彻底清除病毒,恢复健康的网络状态。当取时滞τ=1.07>τ0=1.024 8时,系统(20)在平衡点(0.5,4.0,5.5)处发生Hopf分岔(见图2),说明此时系统在平衡点处是不稳定的,易感节点、感染节点和恢复节点的数量产生了随着时间t的推移而出现的周期振荡,这对于清除病毒,调节和控制网络系统恢复到健康状态是极为不利的。 图1 τ=0.98<τ0时,系统(20)的相图和各分量的波形图 图2 τ=1.07>τ0时,系统(20)的相图和各分量的波形图 下面讨论分数阶的变化对系统(20)的时滞分岔临界点τ0的影响,具体的做法是保持其中两个阶不变,考察另一阶变化对于分岔点的影响。由于时滞τ表示的是因计算机病毒的潜伏期造成的延迟,故处于恢复状态的计算机节点上的分数阶q3的变化对于分岔临界点基本不产生影响(见表1),但是分数阶q1、q2的变化都对分岔临界点有较大的影响。q1从0.5到0.6的变化过程中,时滞τ0随着q1的增大而增大,在0.6到0.7之间出现转折,之后随着q1的不断增大,时滞τ0越来越小(见表1,图3)。而对于分数阶q2,在0.5到1之间,分岔点一直随着q2的增大而增大(见表1,图4)。显然,可以通过调节各变量分数阶的取值来改变系统分岔临界值的大小,从而调节系统的稳定域。 表1 qi变化对于系统(20)Hopf分岔临界值(ω0,τ0)的影响 图3 q2=0.95,q3=0.98时, 系统(20)中τ0随q1的变化 图4 q1=0.92,q3=0.98时, 系统(20)中τ0随q2的变化 上述模拟结果显示,与文献[15]研究的整数阶系统比较,分数阶的引入延迟了系统 Hopf分岔的发生,放大了稳定区间。通过调节分数阶的大小,可以在一定范围内有效控制系统正平衡点的稳定域。分数阶系统获得了比整数阶系统更为灵活的控制方式。 本文通过研究一类具有不同分数阶的时滞计算机病毒传播模型的Hopf分岔,讨论了系统正平衡点的稳定性问题。由于该模型参数较多,首先引入流行病学中基本再生数的概念讨论了系统存在正平衡点的条件。继而以时滞为分岔参数研究系统在正平衡点的稳定性,分析了该模型发生Hopf分岔的3个显式条件,结果表明时滞是造成系统不稳定的主要因素之一,而分数阶的引入不仅以更多的自由度丰富了系统的性能,也影响时滞的变化,继而影响系统正平衡点的稳定域。为了验证理论分析的正确性,选择了恰当的参数做数值模拟,结果说明时滞临界值确实是分数阶计算机病毒模型出现Hopf分岔的一个分水岭。在给定参数值的情况下,时滞的大小是决定系统稳定性的重要因素之一,对于调节和控制系统从病毒侵害状态恢复到健康状态有直接的影响。此外,数值模拟也说明了分数阶变化引起系统Hopf分岔临界值的变化,进一步解释了分数阶对于模型稳定域控制的有效性。 需要指出的是,分数阶模型线性化以后,通过Laplace变换得到对应的特征方程,其纯虚根的求解是基于假设,反代入方程后通过计算求出的,并没有采用理论的方法获得严密的证明,这个具有理论意义的问题将在后续的工作中加以研究。


2 Hopf分岔分析
2.1 平衡点及基本再生数

2.2 正平衡点的稳定性及 Hopf分岔分析

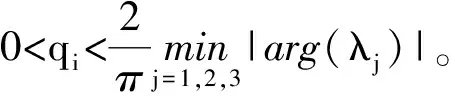






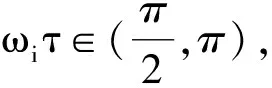




3 数值模拟



4 结论

