浅析转化思想在高中数学解题中的应用
◎ 蒋 刚
高中阶段的数学习题,重点考查了学生思维的灵活性与逻辑性。许多高中生的解题思维比较简单,面对例题时,常常会觉得这些题的思路比较明确,而在遇到类似的习题时,则又出现无从下手的情况。针对学生的解题问题,转化思想得到了深入应用,它可以将复杂的问题简洁化,帮助学生迅速联想到熟悉的知识点,以减轻解题难度,提高学生做题的准确率。
一、化繁为简
许多数学问题看上去十分复杂,找不到解题的突破口,但只要适当地将题目进行转化。击碎外表那层神秘的“面具”,学生就能一目了然的看清其中的本质。应用转化思想,可以将题目化繁为简,帮助学生捕捉到解题的切入点,从迷雾重重过渡到柳暗花明。
例如:已知有x,y两个未知数,满足函数=0,试问的取值范围为多少? 对于这个问题,学生们往往会感到十分费解,从表面上分析,想要求出的取值范围,就要分别求出x和y的取值范围。而在这个函数中,x的最大值和最小值是否能正好对应y的最大值和最小值,似乎还需要通过图像来进一步判定。由此,这道题的解析思路就变得十分复杂。如果通过转化思想,应用换元法来重新变换这道题目,就能起到化繁为简的目的。
比如,假设k=则y=k(x-2)+2,代入到原式之中,就等于,将原式重新整理,就能联立出x与k之间的函数关系式(1-k2)x2—2(2k2-k+1)x-(4k2-4k-1)=0,随后,令△≥0,就能进一步得出关于k的不等式,从而求出最后的取值范围。由此可见,巧妙应用转化思想,可以将看似复杂的题目转变成单纯的二次函数运算,帮助学生快速找到解题的路径。
二、数形结合
对于高中时期的习题而言,大部分题目都需要采用数形结合的方法来进行解析。而运用数形结合,同样可以将复杂的“数”类问题转化成直观的图形,以起到简化解题思路,提高解题效率的目的。
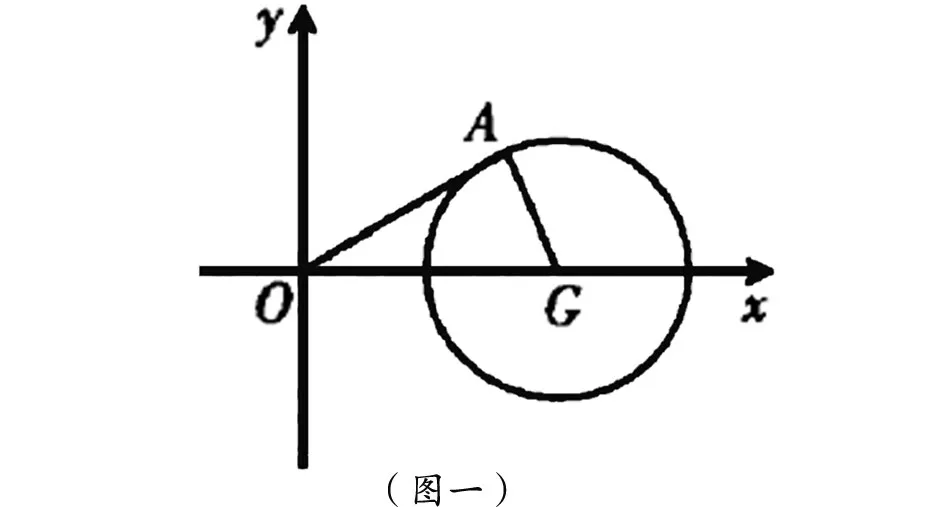
例如:已知有两个实数x,y,满足某函数(x-2)2+y2=1,试求的最大值为多少? 学生在面对这道题时,很容易产生困惑,因为这道函数题与二次函数最值问题的思路截然不同。似乎无法通过对称轴的方式来判定最大值所处的地方。此时,学生就要转换思路,思考这个函数满足什么类型的图像,能否从对应的图像上找到解题的切入点。
从函数的特点上进行分析,该函数明显属于圆心为(2,0),半径为1 的圆形图像。因此,可以在坐标系中绘制出图像(如图一)。通过图像,不难发现可以表示为换言之,也就是过圆上一点(设为A)与原点相连的直线OA的斜率,并求该斜率的最大值。从图形上可见,当直线OA与圆相切时,斜率值最大。此时OA⊥AG,通过计算,不难求出斜率的最大值为
三、正逆转化
观察部分高中数学题,题干的答案往往有非正即反的特点。学生在解题过程中,发现如果按照正面的思路,需要进行大量的分类讨论,解题过程十分复杂。而应用逆向思维,可以另辟蹊径,从未知的角度入手,反向推导出隐藏的已知条件。因此,学生们在解题中遇到困境时,不妨从反面的角度入手,应用转化思想,锻炼逆向思维,从而有效突破难题。
例如:从某个四面体中,提取所有的顶点,以及每一条棱的中点,共能找出10 个点,如果从10 个点中选取4 个不共面的点,那么一共有多少种取法? 学生在解答这道题目时,若采用正面思维,分类讨论的情况将十分复杂,不易进行分析。而将题目的特点进行细致剖析,则可以得出以下结论:除了4 个点不共面以外,其他的情况一定是4 个点共面。因此,学生只要从反面进行思考,找出所有4 个点共面的情况,再从所有的取法中减掉,就能求出该题的最后答案。
通过分析,4 点为同一面的情况可以分为三种情况。第一种:这四个点恰好为四面体的同一个面,而四面体的任意一面都为三角形,根据题意,包括三个顶点和三条边的中点,一共6 个点。那么代入公式计算,共有个4 点同面的情况。第二种:先保证三点为一边,也就是四面体的同一条棱上,剩下的最后一点选择对面棱的中点。这四点满足共面的要求,因为四面体有6 条棱,所以有该情况有6 种可能。此时学生需要注意,不能选择与该棱相近棱上的任意一点,不然会与第一种情况出现重复。第三种,找出四面体中各个三角形面的中位线,也就是相邻两条棱中点的连线。将这些中线进行组合,正好可以构成三个平行四边形。综合以上分析,上述几种情况都不满足题意要求,应当从总数中进行删减,经计算,不难求出最后的答案为141。
四、主次变换
在解答数学题的过程中,通常会遇到主要变量和次要变量。一般来说,主要变量是题干要求解答的目标,而次要变量属于题目中的关键信息。在实际解题中,如果学生直接针对主要变量,计算的过程往往比较复杂。而采用主次变换的方式,调换两种变量的位置,原本繁杂的题目就能变得清晰明了。
如:已知4x+1≥m(x2-1)对于m∈[-3,3]恒成立,试求x的取值范围为多少? 通过这个题目可以判断,主要变量为x,也就是本题所要求解的最终目标。而m为次要变量,也就是题干中给出的关键信息。想要求得x的范围,按照传统的解题思路,通常会将m代入进去,以进行求解。而这种解题方式需要花费大量的精力来完成运算,且很难保证绝对的准确度。因此,需要换一种思路,通过转换思维,来转换两种变量的定位。
解题过程如下:首先,建立关于m的函数f(m),则f(m)=m(x2-1)-4x-1。此时f(m)≤0 恒成立,且m∈[-3,3]。由此可见,当两种变量的主次发生了转变,这道题目就巧妙的转化成了一次函数的图像问题。在此基础上,再进行细致的分析,根据一次函数的公式y=kx+b来进行分类讨论,探究该一次函数图像在[-2,2]之间的单调性问题。通过以上解题过程,学生们不难梳理解题思路,求出最后的答案。
总之,在高中数学解题过程中运用转化思想,可以帮助学生突破固有的解题思路。教师要在解题教学中积极渗透转化思想,让学生能规避掉数学题中的“礁石”,成功化繁为简,从而准确求解出答案。

