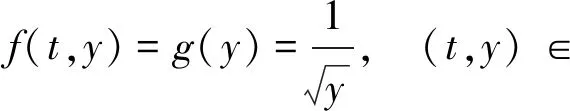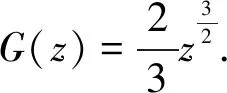一类无穷区间上的非线性三阶奇异边值问题的可解性
包永东,玉琳琨,裴明鹤
(北华大学数学与统计学院,吉林 吉林 132013)
其中q∈C((a,∞),(0,+∞)), f∈C([a,+∞)×(0,+∞),[0,+∞)).综合运用截断函数技巧、Arzela-Ascoli定理和对角化方法,得到上述问题解的新的存在性结果,并给出一个应用例子.
本文研究一类无穷区间上的非线性三阶奇异边值问题
(1)
其中q∈C((a,∞),(0,+∞)),f∈([a,+∞)×(0,+∞),[0,+∞)).
无穷区间上的三阶边值问题在排水流理论、孤立中性原子中的电势、半无穷渗透介质油层的不稳定流等研究中有着广泛的应用.特别地,无穷区间上的三阶奇异边值问题来源于对粘性流体薄膜在重力驱动下于坚固物体表面上流动时的研究.因此,无穷区间上的三阶边值问题受到微分方程学者的广泛关注[1-14].本文的目的是综合运用截断函数技巧和Arzela-Ascoli定理以及对角化方法,建立无穷区间上的三阶奇异边值问题(1)的新的存在性结果.
1 主要结果
首先引入有限区间上的三阶两点边值问题解的一个存在性结果,它是文献[1]中的定理23.1的直接推论.
引理1设a≥0,b>a.假设g:[a,b]×→连续,φ∈C(a,b)∩L1[a,b]并且在区间(a,b)内φ(t)>0.若存在一个不依赖于λ的常数M>a0+(b-a)[b2(b-a)/2+a1],使得对于问题族
(2)λ
定理1假设
(ⅰ)对任意b>a有
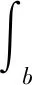
(ⅱ) 存在定义于(0,+∞)上的非增正值连续函数g(u)使得
0≤f(t,u)≤g(u), (t,u)∈(a,∞)×(0,∞),
以及

(ⅲ)存在连续函数ψ:[a,∞)→(0,∞),使得对任意固定的k>a,若y∈C2[a,k]满足
则有
f(t,y(t))≥ψ(t),t∈(a,k),

则问题(1)存在一个解y∈C2[a,∞)∩C3(a,∞)满足y″∈BC[a,∞)和y(t)>0,t∈(a,∞).
证明:固定n∈{1,2,…}且n>a+1.首先讨论有限区间上的奇异边值问题
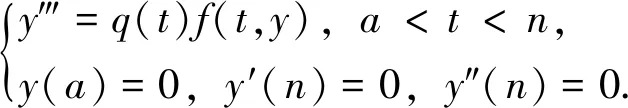
(3)
为此,任取m∈{1,2,…},考虑奇异边值问题
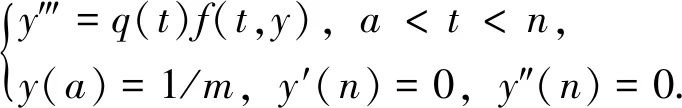
(4)m
为了证明(4)m有一个解,考虑以下修正问题族
(5)λ
其中0<λ<1和
假设y是问题(5)λ的一个解,λ∈(0,1).则y‴(t)≥0,t∈(a,n),y″(t)≤0,y′(t)≥0,y(t)≥1/m,t∈[a,n].注意到
y‴(t)≤q(t)g(1/m),t∈(a,n),
从t到n积分上式得
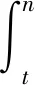
再从t到n积分上式得

进一步从a到t积分上式得
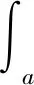
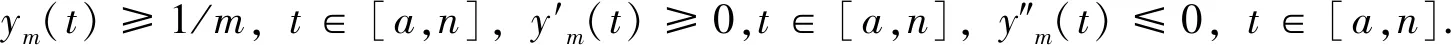
下面,我们证明问题(3)存在一个解.注意到
y‴m(t)≤q(t)g(ym(t)),t∈(a,n),
(6)
从t到n积分上式得
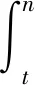
再从t到n积分上式得
从而
(7)
从a到t积分式(7)得
因此

(8)
以及
于是由条件(ⅲ)有
f(t,ym(t))≥ψ(t),t∈(a,n).
(9)
注意到ym满足
所以由式(9)得
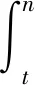
从而
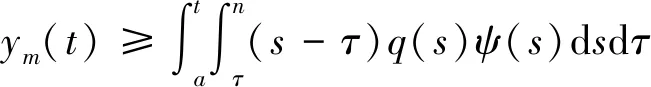
(10)
令
r(t)=ym(t)-(t-a)ym(a+1),t∈[a,a+1].
则r″(t)≤0,t∈[a,a+1],且r(a)=1/m,r(a+1)=0.因此r(t)≥0,t∈[a,a+1],从而
ym(t)≥(t-a)ym(a+1)≥(t-a)Φ(a+1),t∈[a,a+1].
(11)
再令
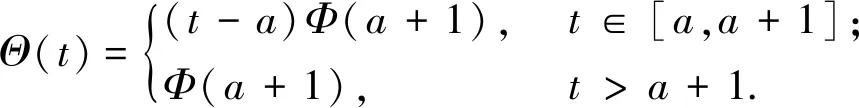
则由式(10)和(11)得
ym(t)≥Θ(t),t∈[a,n].
(12)
因此,由式(6)得
y‴m(t)≤q(t)g(Θ(t)),t∈(a,n),
(13)
从而
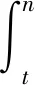
(14)
进而
(15)

注意到,ym(m∈S)满足积分方程
且
ym(s)≥Θ(s)≥Θ(t),s∈[t,n],
所以在上式中,令m→∞(m∈S),并由勒贝格控制收敛定理得
于是
u‴n(t)=q(t)f(t,un(t)),t∈(a,n),u′n(n)=0,u″n(n)=0.
设n0∈{1,2,…}是一个固定的大于a+1的自然数.由前面的证明可知,对于每一个n∈{n0,n0+1,…},问题(5)λ有一个解un(t)满足
un(t)≥Θ(t),t∈[a,n],
和

(16)
选取n∈{n0,n0+1,…}.注意到,式(16)隐含

(17)
从而
(18)
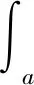
(19)
和
0≤u‴n(t)≤q(t)g(Θ(t)),t∈[a,n0].
(20)


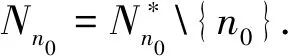


和
0≤u‴n(t)≤q(t)g(Θ(t)),t∈[a,n0+1].
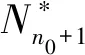


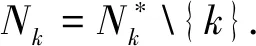
定义一个函数y:[a,∞)→[0,∞)如下:选取t∈[a,∞),并设m∈{n0,n0+1,…}使得t (21) (22) 任意取定m∈{n0,n0+1,…}.设t∈(a,m),则对于n∈Nm,有 令n→∞(n∈Nm) 得 即 因此y‴(t)=q(t)f(t,y(t)),a y‴(t)=q(t)f(t,y(t)),t∈(a,∞), 例1考虑无穷区间上的三阶奇异两点边值问题 (23) 令 则 因此 综上,问题(23)满足定理1的所有条件,所以问题(23)存在一个解y∈C2[1,∞)∩C3(1,∞)满足y″∈BC[1,∞),y(t)>0,t∈(1,∞).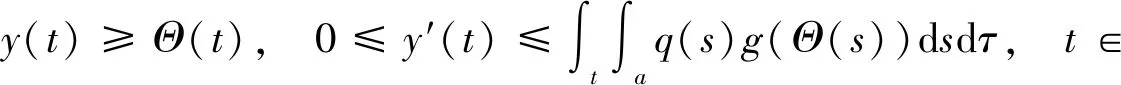

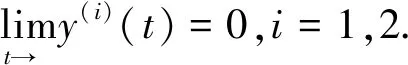
2 应用举例