等应力比加载下颗粒材料的宏细观定量关系探讨
路德春, 张世浩, 田 雨, 杜修力
(北京工业大学岩土与地下工程研究所, 北京 100124)
土是由颗粒构成的离散介质,外力能够引起细观上土颗粒排列方式的改变,同时颗粒排列也能影响宏观上土体的变形、强度等力学特性,因此宏细观2种尺度之间存在着密切联系.
离散单元法是研究宏细观联系的主要手段,该方法自Cundall等[1]提出后,在模型建立、算法实现、接触本构等方面得到快速发展,可以实时监测加载过程中的颗粒位置及颗粒间接触情况. 利用该方法,国内外学者开展了大量数值模拟. 在简单加载条件下,Garcia等[2]进行了大量的直剪试验模拟,探究颗粒形状对抗剪强度的影响规律. Nouguier-Lehon等[3]对不规则多边形颗粒进行了一系列双轴压缩数值试验,结果表明随颗粒长径比的增加,试样达到临界状态所需的应变逐渐增加. 吴越等[4]采用几种不同的制样方式,研究了初始各向异性程度对剪胀性及临界状态的影响规律. 蒋明镜等[5]分析了颗粒排列方向对试样变形和强度的影响,发现随着沉积角的增加,试样的剪胀程度逐渐减弱,残余内摩擦角逐渐减小. 在复杂加载条件下,刘洋等[6-7]使用颗粒流软件PFC2D开展循环加载试验,分析了松砂和密砂的颗粒配位数、粒间接触力等细观物理量在渐进破坏中的演化规律. 周健等[8]分析了细观组构变化对宏观力学响应的影响,探究了砂土液化的细观机制. Sazzad等[9]发现,颗粒间摩擦角的取值越大,循环加载时应力- 应变滞回圈变得越来越窄. Phusing等[10]模拟了4种循环三轴压缩试验,采用配位数和滑动接触率解释了循环加载中的宏观力学行为. 以上离散元模拟表明,颗粒形状、排列等细观结构特征与试样变形、强度等宏观力学性质之间有着密切联系,但上述研究仅仅对这一联系进行了定性分析,尚未给出宏细观之间的定量关系.
受限于颗粒材料力学性质的复杂性,宏细观定量关系的研究相对较少,一些学者主要是通过改变离散元模拟中颗粒细观参数的取值,获得细观参数与宏观力学参数之间的拟合关系式. 例如,Yang等[11]提出了平行黏结模型中颗粒刚度、颗粒尺寸等细观参数和弹性模量、泊松比等宏观力学指标之间的经验公式. 徐小敏等[12]对离散元模拟和室内三轴试验结果做回归分析,建立了宏细观弹性参数之间的经验公式. 孔亮等[13]采用形状系数量化颗粒的圆度和凹凸度,通过双轴试验离散元模拟提出了峰值强度和形状系数的拟合公式. 周博等[14]研究了颗粒黏结强度、摩擦因数、刚度比等细观参数和材料抗剪强度指标之间的相关性. 除了建立宏细观参数之间的关系式以外,Zhao等[15]根据应力张量和组构张量的乘积定义了一个标量,发现在临界状态时,该标量的取值与中主应力系数无关,可以表示成平均有效正应力的单变量函数. 从以上文献综述中可以发现,关于颗粒材料宏细观定量关系的研究,还处在探索阶段. 一些学者建立的细观接触模型参数与宏观本构模型参数之间的关系式,与所选取的模型有关. 若能得到组构张量与应力张量之间的关系,则可以在现有的很多宏观模型的基础上,发展多尺度本构模型,既能描述颗粒材料的变形机理,又能在实际工程中得到应用.
为了建立宏细观之间的定量联系,本文开展了一系列应力比保持恒定的双轴压缩离散元模拟,分析颗粒之间的接触力(细观量)与试样受到的外力(宏观量)之间的规律,得到了材料各向异性程度与应力比的函数关系式,进而构建了组构张量与应力张量的隐式定量联系.
1 等应力比离散元模拟
土体的变形、强度等宏观力学特性与土颗粒的大小、形状、排列方式等细观结构特征之间有着密切联系. 在加载过程中,随着应力状态的改变,颗粒的排列方式不断演化,因而直接建立复杂加载条件下的宏细观定量关系是十分困难的. 为简化起见,本文采用离散单元法,开展等应力比双轴压缩试验,此时宏观物理量(即应力比)是明确且恒定的,只需要观察细观物理量(即颗粒组构)是如何演化的,从而减少了宏细观关系式的变量个数. 之所以采用等应力比这种加载方式,也是考虑到颗粒材料具有摩擦特性,决定其屈服和破坏的是应力比,而并非某一应力的绝对值,通过对比不同应力比下的试验结果,可以更直观地研究颗粒材料的变形和强度规律.
1.1 加载方案
借助二维颗粒流程序PFC2D开展一系列双轴压缩模拟. 采用ball distribute功能,生成一个初始尺寸为70 mm×70 mm、孔隙率为0.15的试样. 其中颗粒均为圆形,直径为0.1~0.6 mm,密度为2 500 kg/m3,总数超过9 000个. 然后,为了保证颗粒的初始排列为各向同性,给试样施加100 kPa的等向压力. 将按上述方法制得的试样保存,记录每个颗粒的位置以及颗粒间接触力的大小和方向,后续加载均在此颗粒排列的基础上进行.
在等应力比加载过程中,竖向应力σy从100 kPa开始,每个增量步增加5 kPa;同时,等比例地施加水平应力σx,使得σy与σx的比值r始终不变.共进行10组数值试验,r的取值分别为1.1,1.2,…,2.0.以r=2为例,加载开始时,σy=100 kPa,σx=50 kPa,第一个增量步完成后,σy增加至105 kPa,而σx变为52.5 kPa.等应力比加载相当于对试样进行各向异性压缩,试样内部的颗粒排列将随之发生改变,以适应外荷载的变化.在加载过程中,实时监测颗粒之间接触的变化,直至接触法向的空间分布达到基本稳定.
1.2 模拟参数
在PFC2D中,颗粒本身被视为不可变形的刚体,但允许相邻两颗粒存在一定程度的重叠,并根据重叠量的大小,通过接触模型计算颗粒间的接触力. 本文采用最简单的线性接触模型,来探究宏细观之间的定量联系. 模型参数的取值参考蒋明镜等[16]的推荐值,如表1所示,该组参数已被证明能够使得离散元模拟结果与室内试验结果基本一致.
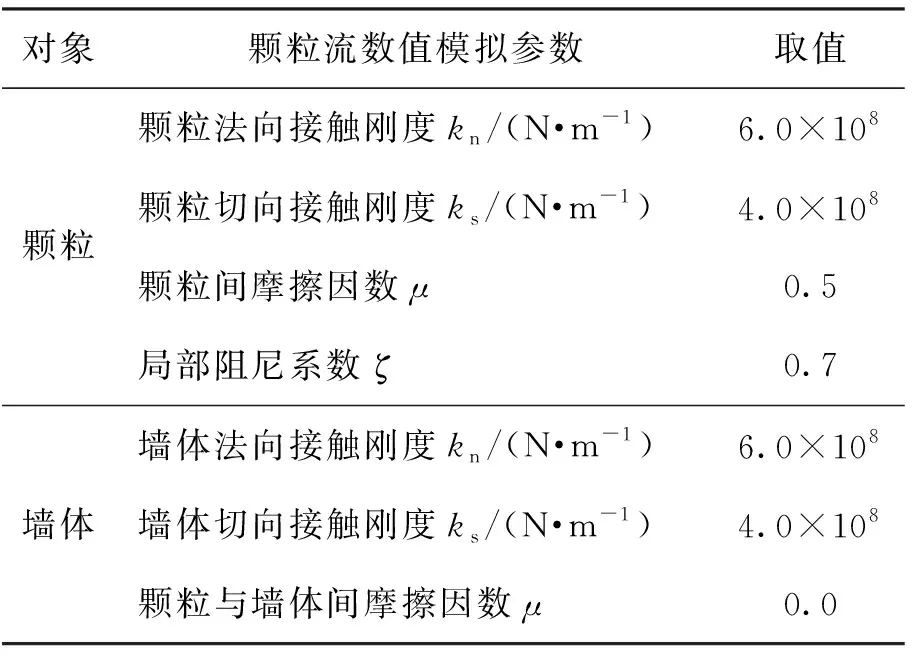
表1 数值模拟参数
2 模拟结果及定性分析
首先,通过观察双轴压缩过程中颗粒间接触力的传递和接触法向的空间分布,定性地分析二者与应力比之间的规律,为下文建立宏细观之间的定量关系提供依据.
2.1 接触力的传递
由于采用圆形颗粒,将相邻两颗粒的圆心相连,即可得到法向接触力的作用轨迹,如图1所示. 该图能够显示外荷载是如何在试样内部传递的,图中连线的粗细反映接触力的大小. 图1分别对应初始状态,以及r=1.5、2.0的等应力比加载的稳定时刻. 可知,在等应力比加载前,各方向接触力的传递较为均衡,连线的粗细也相差不大,表明接触力的大小在不同方向上基本相同,试样为各向同性. 经过等应力比加载后,水平方向的接触力减弱、甚至部分消失,竖直方向成为接触力传递的主导方向. 另一方面,通过连线粗细的变化可以看出,随着应力比的增大,竖直方向的接触力较水平方向越来越大. 特别是当r=2.0时,可以很明显地看到几条自上而下的接触力链(见图1(c)的放大区域),这是试样为承受外荷载而形成的各向异性细观结构.

图1 不同应力比下的接触力链Fig.1 Contact force chains under different stress ratios
由以上分析可知,颗粒间接触力(细观物理量)的方向、大小受外荷载(宏观物理量)的方向、大小的显著影响. 当某一方向上的应力较大时,该方向成为接触力传递的主导方向,其接触力的大小明显高于其他方向. 因此,宏观应力与细观接触力之间存在密切联系.
2.2 接触法向的空间分布
为了更加直观地分析颗粒排列的各向异性,统计了颗粒之间所有接触法向的空间分布情况,绘出玫瑰图,如图2所示. 采用极坐标系,每个扇形对应的转角,等于接触法向与水平方向的夹角;扇形的半径,表示该方向上的接触数占总接触数的百分比. 根据图2(a)可知,初始状态时,各方向接触法向的数目基本相同,表明颗粒排列接近各向同性. 而图2(b)~(d)显示,在等应力比加载完成后,接触法向的空间分布发生显著变化,竖直方向(即转角等于90°)的接触法向明显增多,且当r=2.0时,将近12%的接触法向沿着竖直方向,而沿水平方向(即转角等于0°或180°)的接触法向数仅占总数的7%~8%.
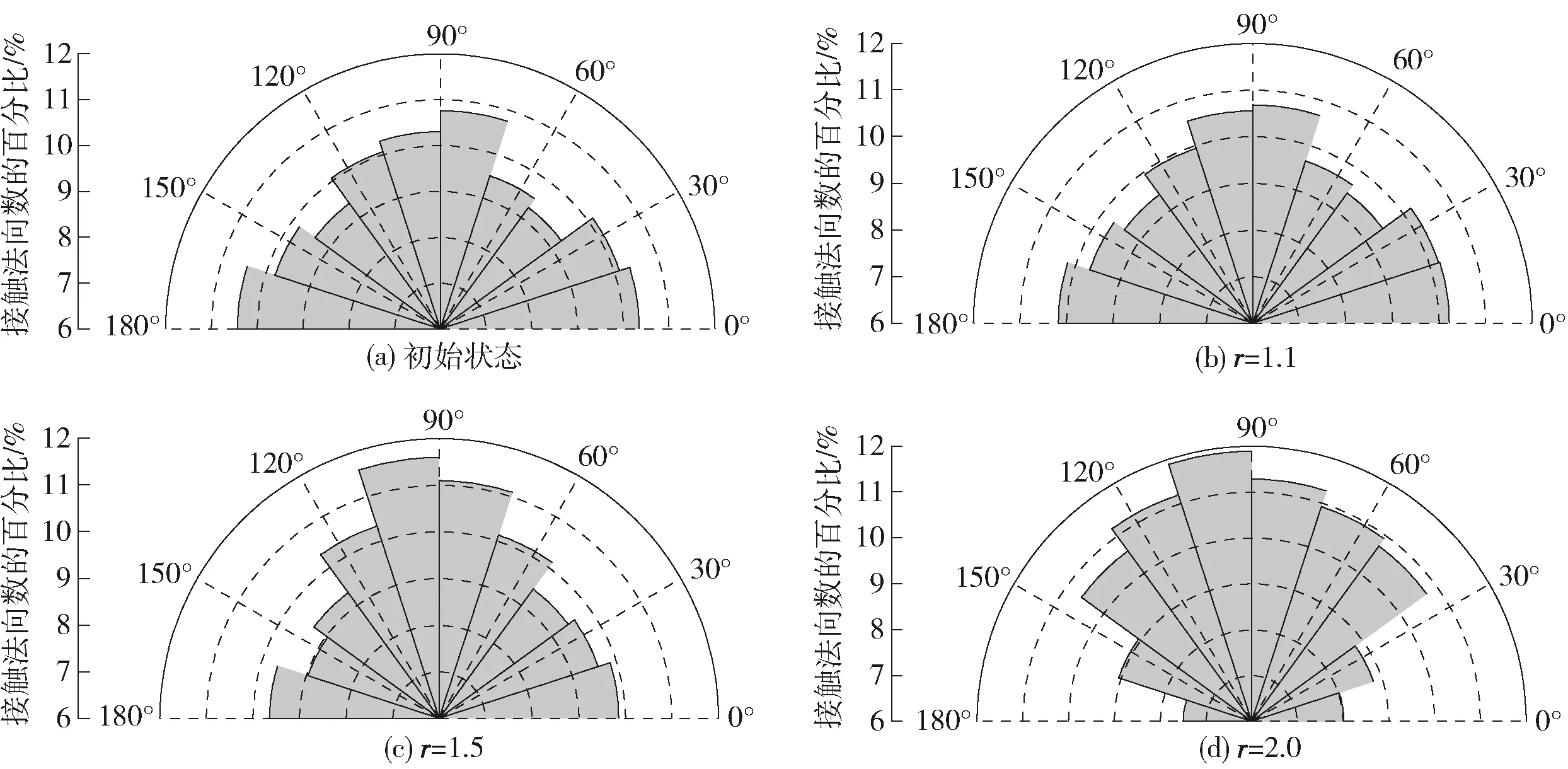
图2 不同应力比下接触法向的空间分布Fig.2 Spatial distribution of contact normal under different stress ratios
3 组构张量及其演化
在定性分析的基础上引入组构张量的概念,定量地描述接触法向的空间分布及其演化规律,进而寻找宏细观之间的定量关系.
3.1 组构张量的定义
组构张量是描述颗粒材料各向异性的物理量,可以根据颗粒长轴方向[17]、孔隙长轴方向[18]、接触法向[19]等细观几何要素进行定义. 由于本文的离散元模拟采用圆形颗粒,不存在颗粒长轴,但接触法向能够非常方便地确定;而且有研究表明[20],相比于颗粒长轴方向和孔隙长轴方向,接触法向对应力的敏感程度更高,更容易随着外荷载的改变而实时调整其空间分布,因此本文利用接触法向来定义组构张量. 如图3所示,接触法向垂直于相邻两颗粒的公切线,与颗粒圆心连线的方向相同,沿该方向的单位向量为n=(nx,ny)(x轴沿水平方向,y轴沿竖直方向),参考Oda[21]的定义式,计算组构张量

图3 组构张量的定义Fig.3 Definition of fabric tensor
(1)

3.2 组构演化规律
直接分析一个二阶张量的变化规律较为困难,因此,首先引入Fij的第二偏不变量
(2)
式中:δij为Kronecker符号(当i=j时,δij=1;当i≠j时,δij=0).因此,当且仅当Fij=δij/2,即试样为各向同性时,J才等于0;否则J≠0,代表试样为各向异性,且J值越大,各向异性程度越高.
在等应力比加载过程中,通过对接触法向的实时监测,得到了J随竖直应力σy的演化规律,如图4所示.以应力比r=1.5的曲线为例进行分析.在加载初期,J接近0,说明此时试样基本处于各向同性状态.随着σy的提高,J逐渐增大,试样的各向异性程度变大,这是因为颗粒之间的接触法向在不断调整,趋向于竖直方向.此后,J的增长速率逐渐变缓,最终收敛到一个稳定值,外荷载的继续提高不会改变试样内部的细观结构,颗粒排列已达到稳定状态.对比不同应力比加载下的J演化曲线,可以看出:r越大,J增长速度越快,表明接触法向的调整变得更加迅速;另一方面,最终J的稳定值也越来越大,且对应的σy越来越高,这说明试样需要施加更大的外荷载才能达到稳定,所形成的细观结构具有更强的各向异性程度.
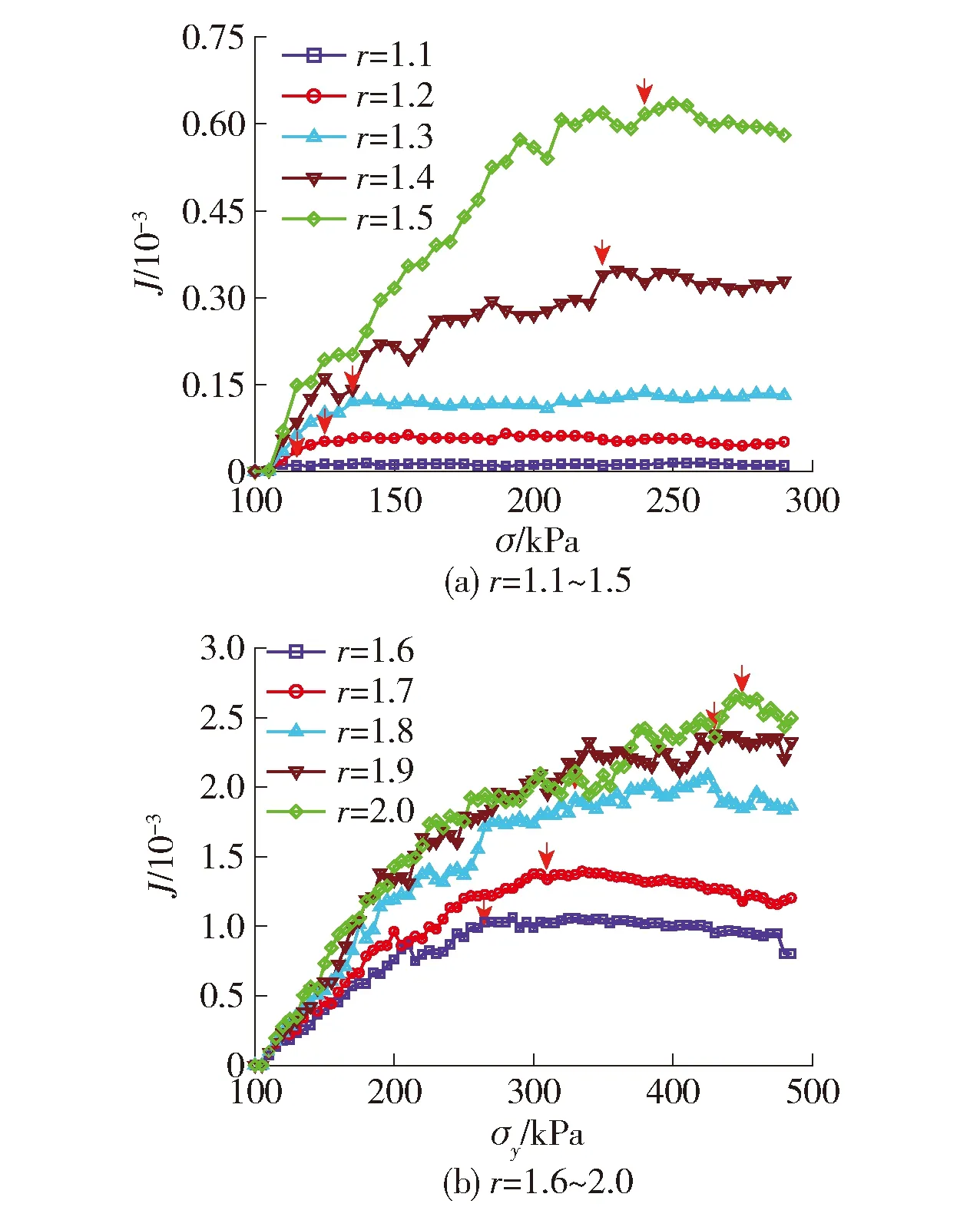
图4 不同应力比下第二偏不变量的演化规律Fig.4 Evolution of the second partial invariant under different stress ratios
3.3 稳定时的组构值
由于J值在σy较大时仍不断波动,仅凭肉眼观察确定J的稳定值具有很强的主观性,因此引入统计学中的变异系数δ作为判断J是否达到稳定的标准,其表达式为
(3)

图5的横坐标为应力比r,纵坐标为相应的Js.由图可知,当r∈[1.1~2.0]时,随着r的增大,Js逐渐增长(说明颗粒排列达到稳定时的各向异性程度更高),且增长速度越来越快.这一规律可用二次函数描述,即

图5 第二偏不变量的稳定值与应力比的关系Fig.5 Relation between the stable value of the second partial invariant and the stress ratio
Js=a(r-1)2
(4)
式中a为反映Js增长速度的系数.与数值模拟结果的对比表明,式(4)可以很好地拟合Js随r的变化规律,相关系数R2达到0.991.而且,当r=1时,根据式(4)可得Js=0,这符合等向压缩条件下颗粒排列最终演化成各向同性的试验规律.
3.4 适用性分析
式(4)是在特定情况下得到的拟合结果,为了检验其对其他情况的适用性,调整了颗粒的初始排列方式和摩擦因数的取值,采用相同的等应力比加载和数据处理方法,分析了上述2种因素对模拟结果的影响.
通过对随机生成的试样施加100 kPa的等向预压力,获得初始各向同性试样;为得到各向异性试样,将某方向的预压力提高,进行非等向压缩,使得颗粒的初始排列产生一定的方向性,再进行r=1.8下的等应力比加载.得到的J值随σy的演化规律如图6所示.对于试样I,水平方向的预压力大于竖直方向,因此初始时颗粒间的接触力以水平方向为主(Fxx>Fyy).在等应力比加载阶段,随着σy的提高,原本占主导的水平接触力逐渐减弱,试样变为各向同性(Fxx=Fyy),因此J先减小到0.然后,随着竖向接触力的生成和不断发展,竖直方向成为接触力传递的主导方向(Fxx 图6 初始颗粒排列对组构演化的影响Fig.6 Effect of the initial particle arrangement on fabric evolution 图7为颗粒间摩擦因数μ分别取0.3、0.4、0.5时,Js随r的变化规律.可知,在其他条件相同的情况下,μ的取值对Js有一定影响,因为颗粒间的摩擦力(即切向接触力)也能够分担一部分外荷载,从而改变最终稳定时的颗粒排列方式.然而,μ只能影响拟合系数a的大小,而在本文的模拟条件下,Js与r的二次关系仍然成立,且相关系数R2均大于0.980. 图7 颗粒间摩擦系数对第二偏不变量的稳定值的影响Fig.7 Effect of the particle friction coefficient on the stable value of the second partial invariant 得到了组构张量的第二偏不变量J与应力比r的公式,初步建立了宏细观之间的定量联系,但J和r都是标量,只能反映组构和应力的各向异性程度的大小,而无法表示二者的方向.若要全面考虑大小和方向,需要建立组构张量Fij与应力张量σij的关系式,即Fij=f(σij)或σij=f(Fij).然而,直接得到2个张量之间的显式方程较为困难.本文借鉴Zhao等[15]的方法,先将Fij与σij以不同形式组合,得到一个新的二阶张量;若该组合张量与加载方式无关,即f(Fij,σij)=C(C为常数),说明Fij与σij始终满足一个隐式函数关系.该隐式函数也能够描述宏细观定量关系. 4.1Fij与σij的组合形式 首先,细观物理量,即组构张量Fij的定义式见式(1);而对于宏观物理量,根据双轴压缩模拟中竖直和水平加载板上的平均应力,得到应力张量 (5) 为了消除应力大小的影响,将σij各元素都除以平均正应力p(p=(σy+σx)/2),得到量纲一的应力比张量 (6) 在等应力比加载过程中,ηij不发生变化. 然后,将Fij与ηij以不同形式做点积,构造了如下几种组合张量: (7) (8) (9) 仿照式(2),求出颗粒排列达到稳定状态时Xij对应的第二偏不变量,仍记为Js,进而绘出Js与r的关系,如图8所示.因为对于不同形式的Xij,Js的变化范围有所不同,所以利用r=1.1时的Js值进行了归一化,以便比较Js随r的相对变化情况. 图8 各种组合张量的第二偏不变量随应力比的变化规律Fig.8 Variation of the second partial invariants of different joint tensors with stress ratio 需要说明的是,根据Zhao等[15]的工作,在临界状态,即应力比等于临界状态应力比时,Fij与σij的某种联合不变量,是一个与中主应力系数无关的常量.本文的工作可视为对上述规律的发展,即在应力比达到临界状态应力比之前,试样压缩稳定(颗粒排列不再随应力的增加而改变)时Fij与σij的某种组合,也是一个常量. 为了得到颗粒材料宏细观之间的定量关系,本文在离散元模拟中进行了大幅简化:颗粒形状为圆形,所有颗粒之间的摩擦因数取均一值,并且采用二维模拟,加载条件为等应力比压缩,直至颗粒排列达到稳定状态.而实际中,土颗粒的细观特性十分复杂,土体受到的应力状态多种多样,因此本文所建立的宏细观定量关系式存在一定的局限性,相关问题还应进行深入研究,以更加贴近真实情况. 1) 在等应力比加载过程中,大主应力方向逐渐成为颗粒间接触力传递的主导方向,且应力比越大,这一趋势越明显,颗粒排列的各向异性程度越高. 2) 随着外荷载的增加,组构张量的第二偏不变量逐渐趋于一个稳定值,该稳定值与应力比呈二次函数关系,且这种关系不随颗粒的初始排列方式、摩擦因数取值的改变而变化. 3) 将颗粒排列达到稳定时的组构张量与应力张量按某种形式进行组合,该组合张量与应力比无关,从而建立了组构张量和应力张量的隐式关系.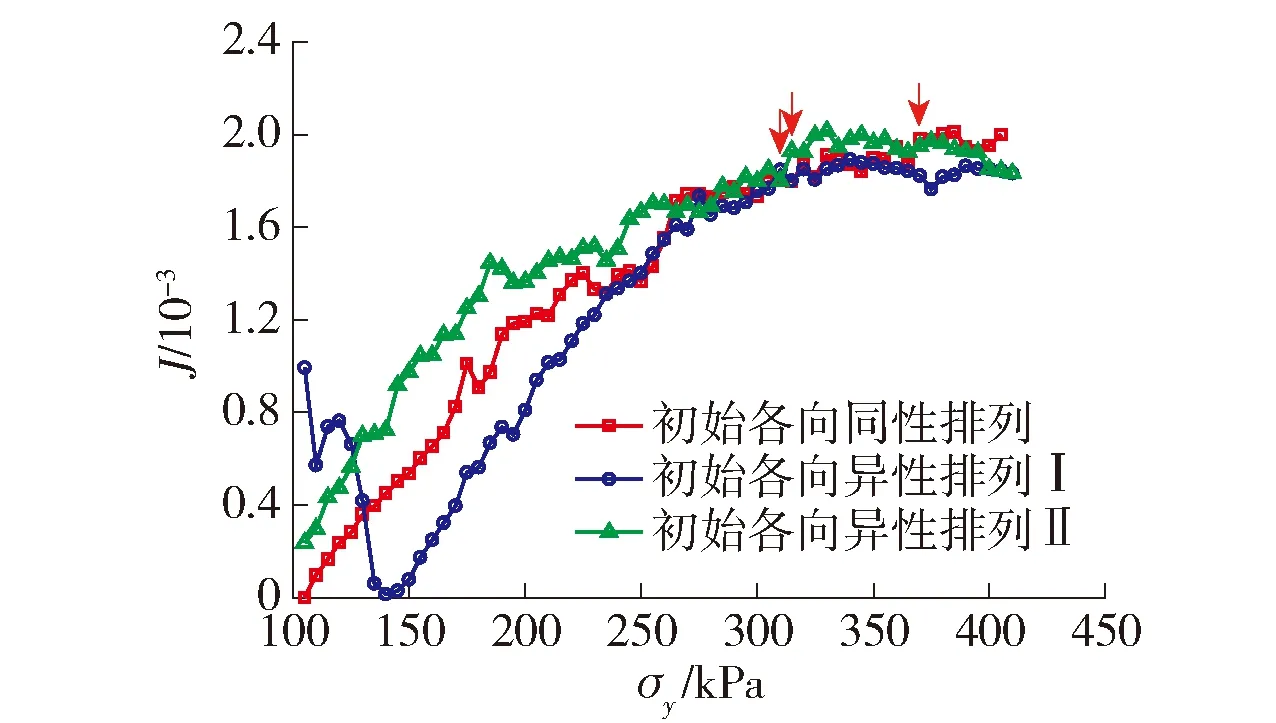

4 组构张量与应力张量的定量联系
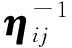
4.2 组合张量随应力比的变化规律



5 结论

