求解对流扩散反应方程的一种高精度紧致差分方法
杨苗苗, 葛永斌
(宁夏大学 数学统计学院,宁夏 银川750021)
对流扩散反应方程作为一种基本的运动方程,在很多科学和工程技术领域都有着非常广泛地应用,可用于描述流体的流动与传热、燃烧与爆炸、核工业中反应堆的冷却及工业生产中化学堆的反应等现象.因此对于该类方程精确数值解的研究具有很高的理论价值和实际作用.
求解该类方程的方法有很多种,最常用的是有限差分法.目前已经发展了很多具有高精度并且紧致的差分格式,如针对对流扩散方程:Sun等[1]利用理查森外推法与算子插值法改进了四阶紧致差分公式,使格式具有六阶精度;田振夫[2]在迎风变换的基础上,将对流扩散方程转化成含源纯扩散方程,并利用Hermite法推导出指数型的差分格式,具有四阶精度;梁昌弘等[3]利用3个点上的未知函数值及四阶Padé格式将一阶导数代换的方法,借助显式紧致格式和隐式紧致格式的思想,得到了一种性能更优的四阶混合型格式;Tian等[4]建立了一种可用于求解定常对流扩散方程的高精度指数型有限差分格式,适合大梯度问题或边界层问题的求解;Chen等[5]在差分格式的构造中将摄动方法与一阶迎风格式相结合,得到了求解二维定常对流扩散方程的一种高精度格式;Gupta等[6]采用泰勒级数展开法得到具有四阶精度的有限差分格式;Spotz[7]则利用截断误差余项修正的方法给出了一种多项式型的四阶紧致差分格式.尽管文献[6-7]格式的推导方法不一样,但本质上是同一格式;Zhao等[8]将该方法推广到变系数的对流扩散反应方程中,还给出了所得格式的收敛性分析;刘明会[9]基于原方程代入和四阶紧致差分公式法,将二阶导数代替后得到了一种新的格式.文献[8-9]格式尽管推导过程及方法不一样,但本质上仍是同一格式.田振夫[10]用截断误差余项修正法,将余项中的三阶导数和四阶导数用一阶和二阶导数替换,代入原方程整理便得到四阶精度的差分格式,将该方法推广到二维后,则得文献[11]中的格式;其他针对对流扩散反应方程的数值求解方法还有,魏剑英[12]首先由常系数变易法得到3个点上的指数型差分格式,再利用源项在中心点做二阶泰勒级数展开,得到求解常系数的四阶差分格式;田芳等[13]借助常系数指数型高精度紧致差分格式,采用残量修正法得到变系数对流扩散反应方程的紧致差分格式;田芳等[14]还基于泰勒级数展开,给出了一、二阶导数的表达式,构造了非均匀网格上的对流扩散反应方程的多项式型的差分格式;兰斌等[15]采用坐标变换法将原方程由物理空间的非均匀网格变换为计算空间的均匀网格,再结合中心差分格式得到了求解对流扩散反应方程的紧致差分格式.
本文针对一维、二维定常对流扩散反应方程,基于截断误差余项修正的方法推导建立了一种新的紧致差分格式,具有四阶精度.尽管本文方法与文献[7-11]一样采用到了截断误差余项修正法,但本文仅用到了一阶导数的表达式来修正未知函数中的三阶和四阶导数项,而没有用到二阶导数项,这样做的目的是使格式具有更小的耗散误差.
1 一维问题差分格式的建立
首先,考虑如下一维对流扩散反应方程:
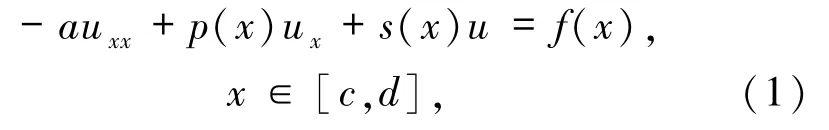
其中a>0为扩散项系数,一般是常数;u(x)是未知函数,p(x)是对流项系数,s(x)是反应项系数,f(x)为源项,并且要求u(x)、p(x)、s(x)、f(x)具有充分的光滑性.当s(x)≡0时,模型方程(1)为对流扩散方程.
将区间[c,d]分为N等份:x i=c+ih,i=0,1,…,N,定义网格步长h=(d-c)/N;中心差分算子:
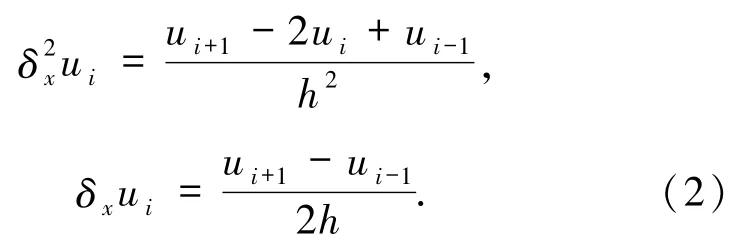
由泰勒级数展开可得:
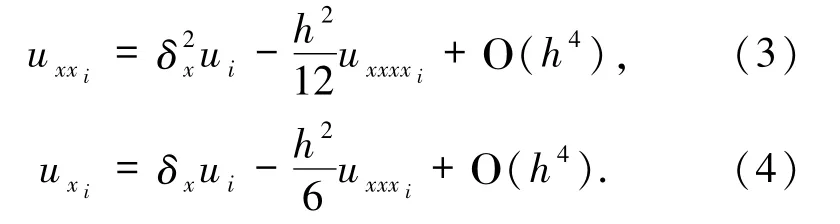
将(3)和(4)式代入(1)式得
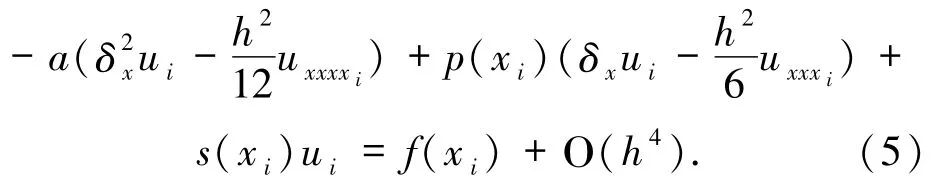
由(1)式得
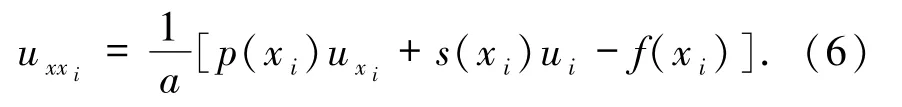
对(6)式两边关于x求导可得
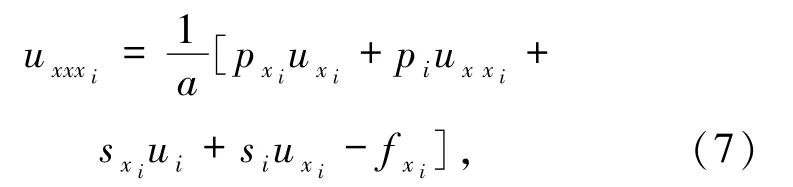
则(7)式为文献[7-10]中处理三阶导数项的方法,即三阶导数由一阶和二阶导数来表示.本文为了减小耗散误差,将(6)式代入(7)式并整理可得
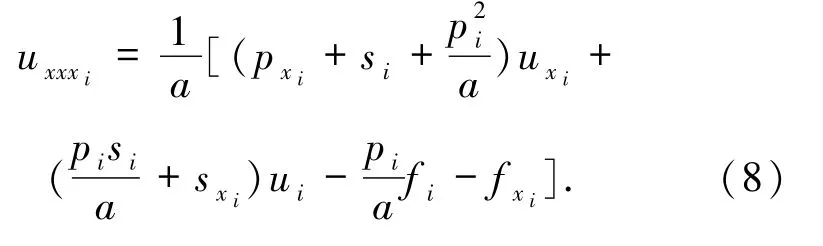
(8)式为本文处理三阶导数项的方法,即u xxx i仅由一阶导数来表示.这是本文格式区别于文献[7-10]的地方.同理,对四阶导数的处理如下:
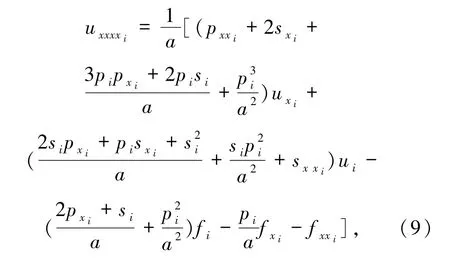
即u xxxx i也仅用到一阶导数u x i,没有如文献[7-10]一样用到二阶导数u xx i.
将(8)和(9)式代入(5)式并舍去 Ο(h4)得

对上式中的对流项和反应项系数的导数利用中心差分公式(2)离散可得由该过程可知,本文格式的截断误差为Ο(h4),即格式(10)在空间上可达四阶精度.对于f(x)的导数项的计算,可直接代入精确解,也可用中心差分离散,并不会影响格式的整体精度.另外,注意到本文一维格式只用到3个网格点,形成三对角型的代数方程组,可采用追赶法进行求解.

2 误差分析
下面分别对格式(10)的耗散误差和色散误差进行分析.
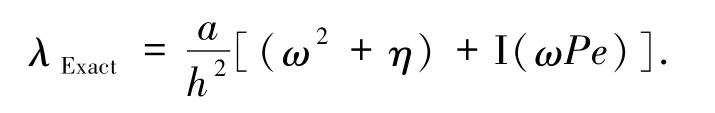
为了简化计算,将本文格式(10)化为常系数
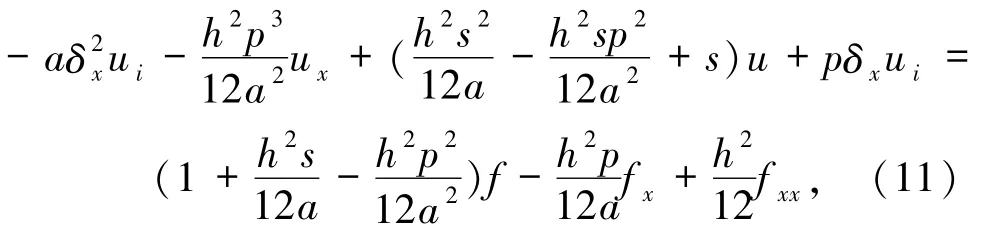
则有

同理
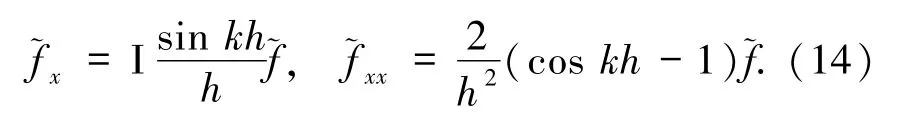
将(12)~(14)式代入(11)式得
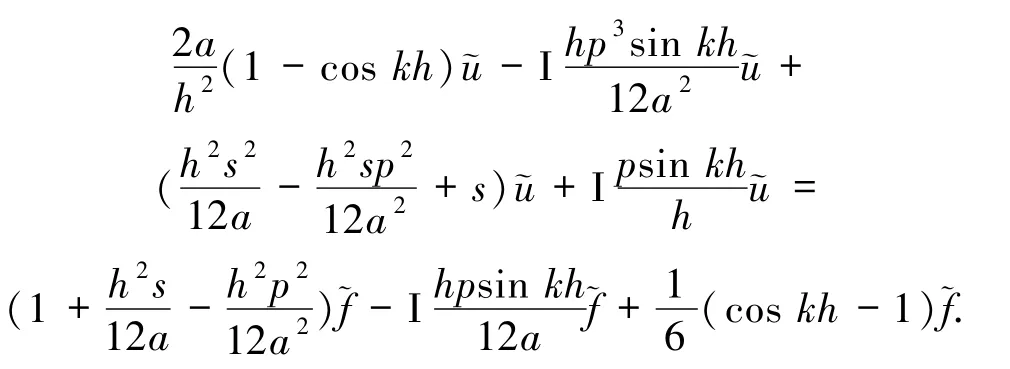
化简得
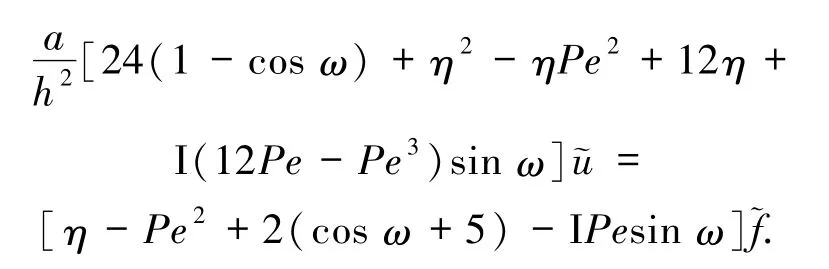
因此,本文差分格式的特征函数可表示为
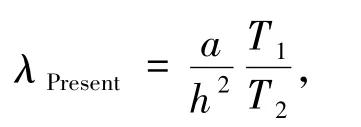
其中
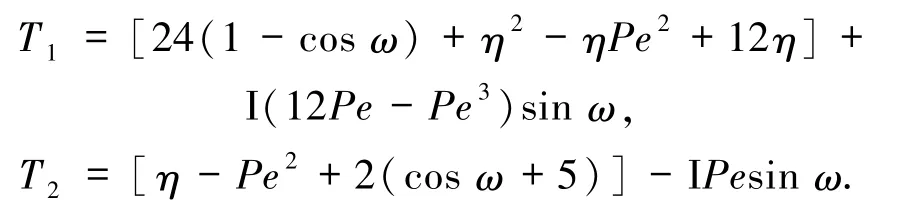
另外,为了进行对比分析,通过计算可得文献[3]中MHOC格式的特征函数为
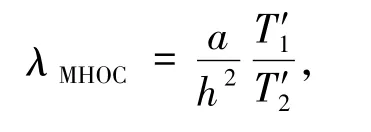
其中
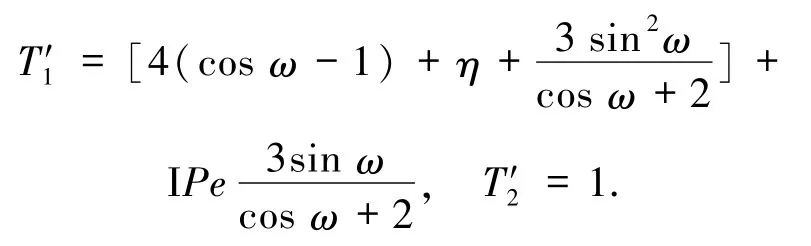
文献[8]中FOC格式的特征函数为
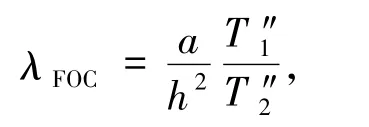
其中
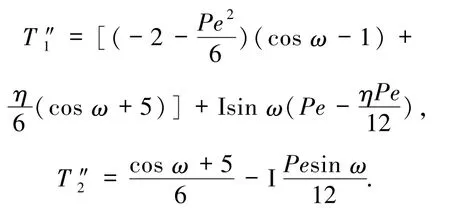
图1~4分别给出了当η=1,Pe取不同数值时,MHOC格式[3]、FOC格式[8]和本文格式的耗散性及色散性的误差分析.不难发现,对耗散误差而言,文本格式比MHOC格式和FOC格式的耗散误差均小;但就色散性而言,本文格式比FOC格式要好,但不及MHOC格式.
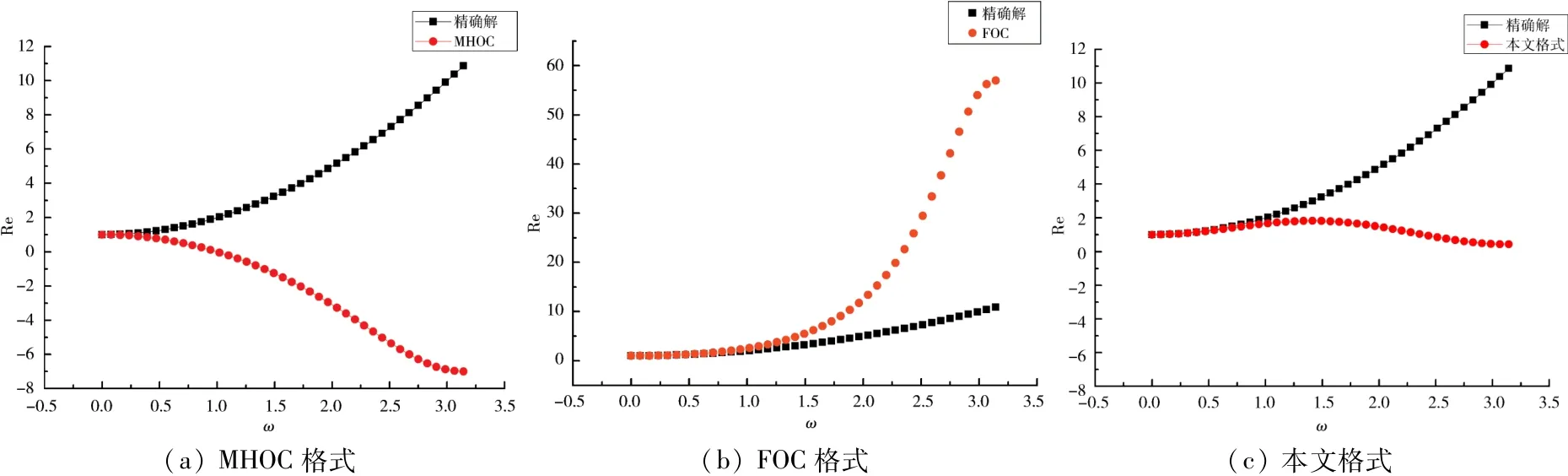
图1 当Pe=10时耗散误差Fig.1 The dissipation error when Pe=10
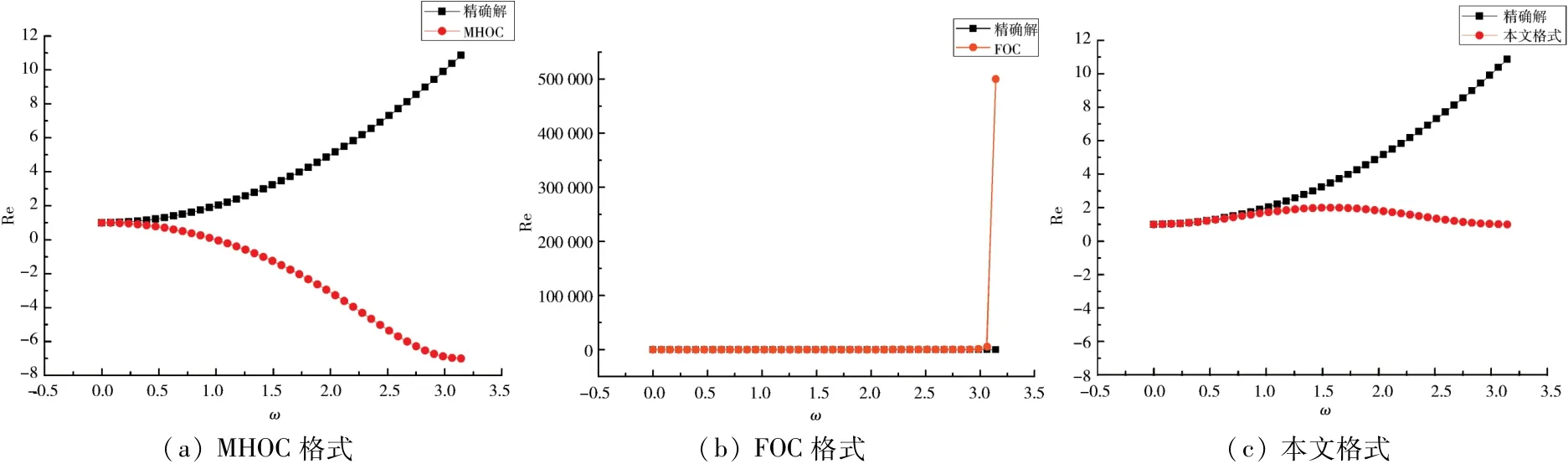
图2 当Pe=1 000时耗散误差Fig.2 The dissipation error when Pe=1 000

图3 当Pe=10时色散误差Fig.3 The dispersion error when Pe=10
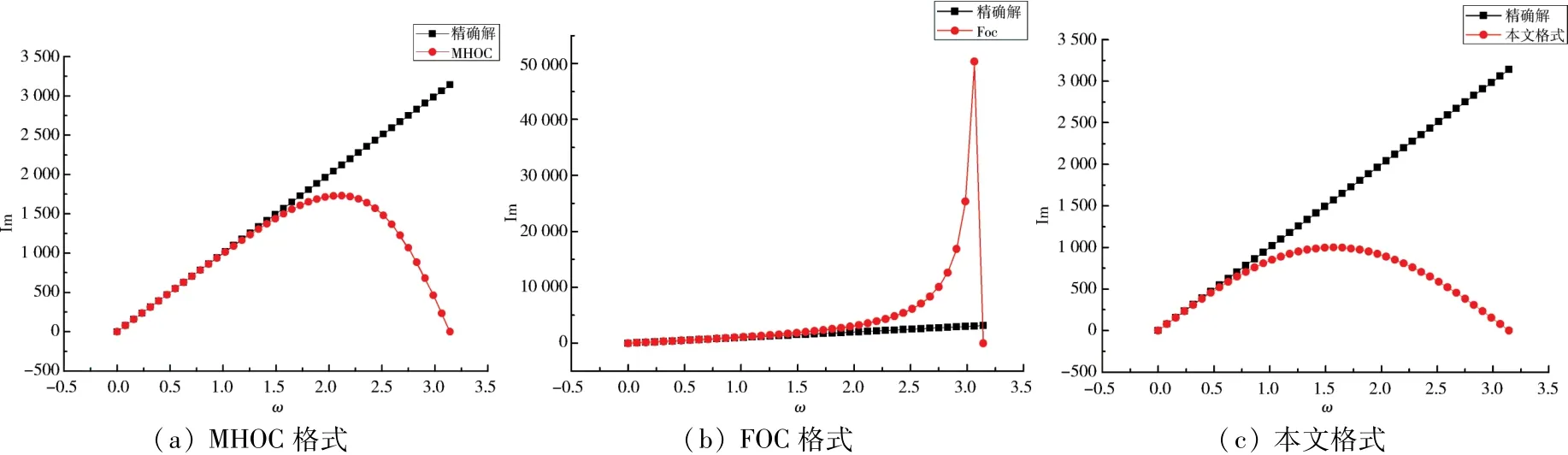
图4 当Pe=1 000时色散误差Fig.4 The dispersion error when Pe=1 000
3 二维问题差分格式的建立
考虑如下二维对流扩散反应方程
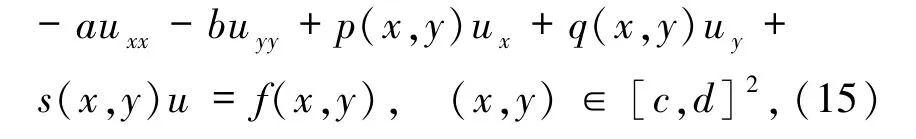
其中,a,b>0为扩散项系数,一般是常数;u(x,y)是未知函数,p(x,y)和q(x,y)是对流项系数,s(x,y)是反应项系数,f(x,y)为源项,并且要求u(x,y)、p(x,y)、q(x,y)、s(x,y)、f(x,y)具有充分的光滑性.
将区间[c,d]分为N等份:x i=c+ih,y j=c+jh,i,j=0,1,…,N,定义网格步长h=(d-c)/N.
将(15)式可转化成如下2个一维形式的方程:
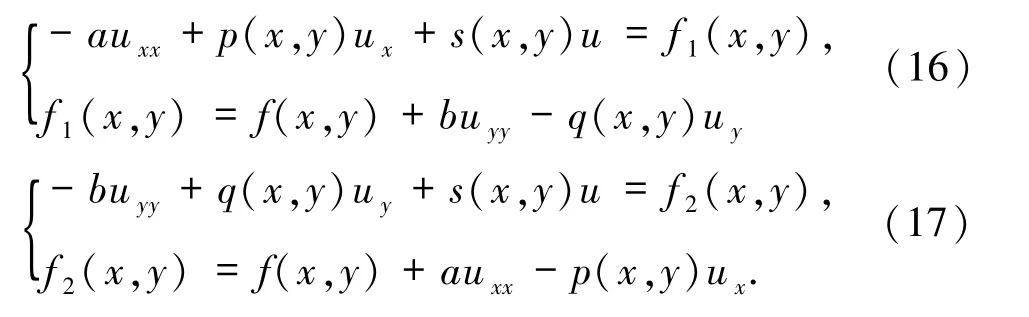
显然方程(16)和(17)从形式上看可认为是一维的.因此,可直接利用一维对流扩散反应方程的四阶精度差分方法对其进行离散,即可得在x方向有
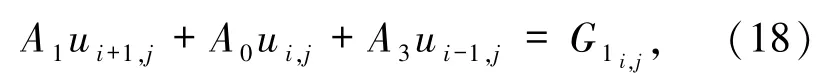
其中
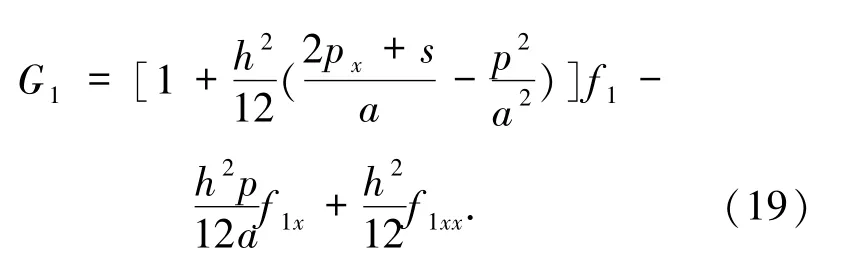
对(16)式中f1(x,y)两边关于x求偏导,可得:
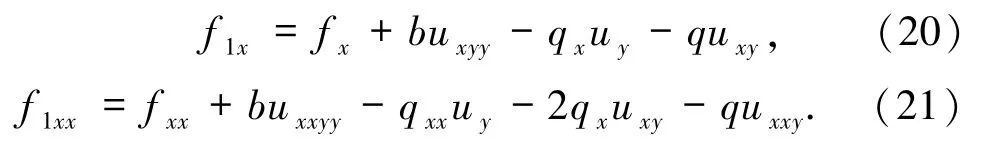
将(20)和(21)式代入(19)式整理得
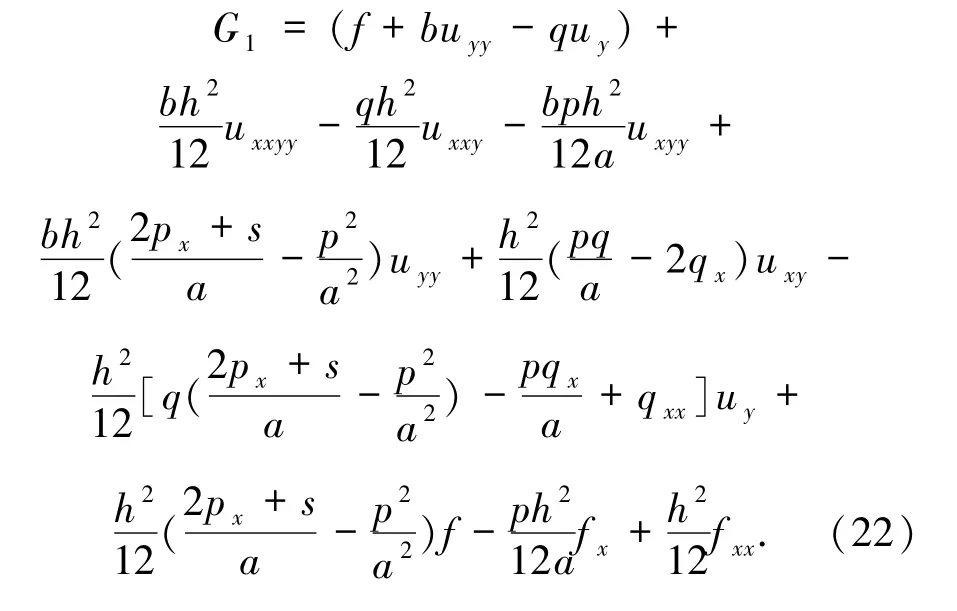
同理可得在y方向有
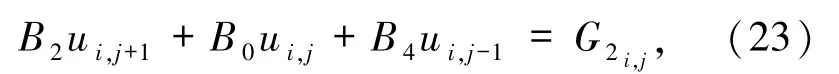
其中
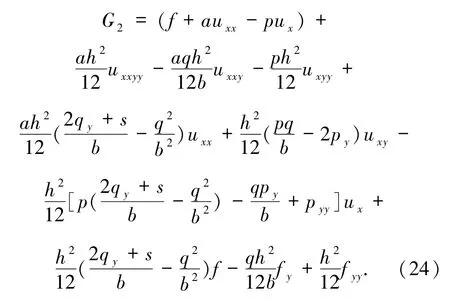
于是有
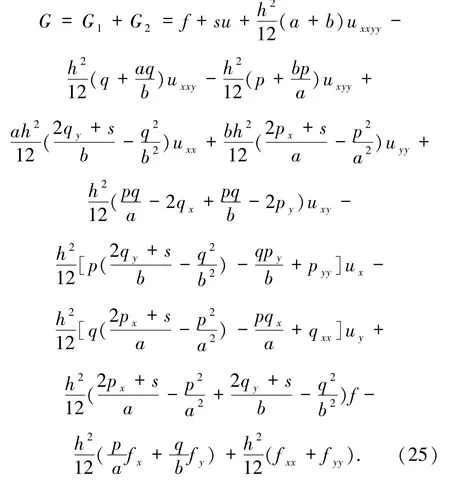
注意(15)式为一种辅助关系,由(18)和(23)式的离散整理可得
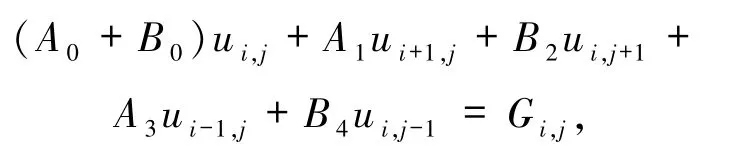
其中
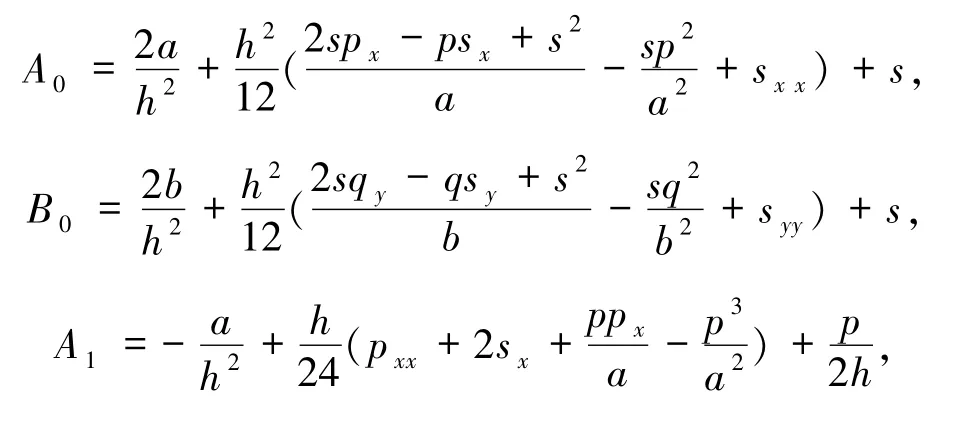
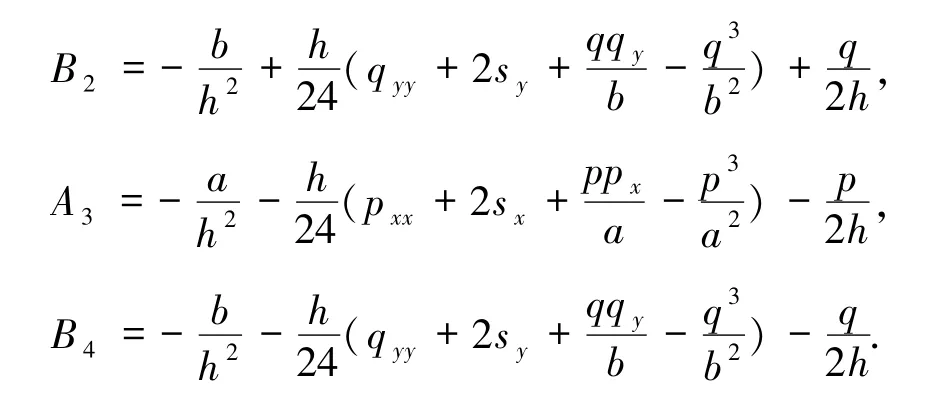
定义中心差分算子:
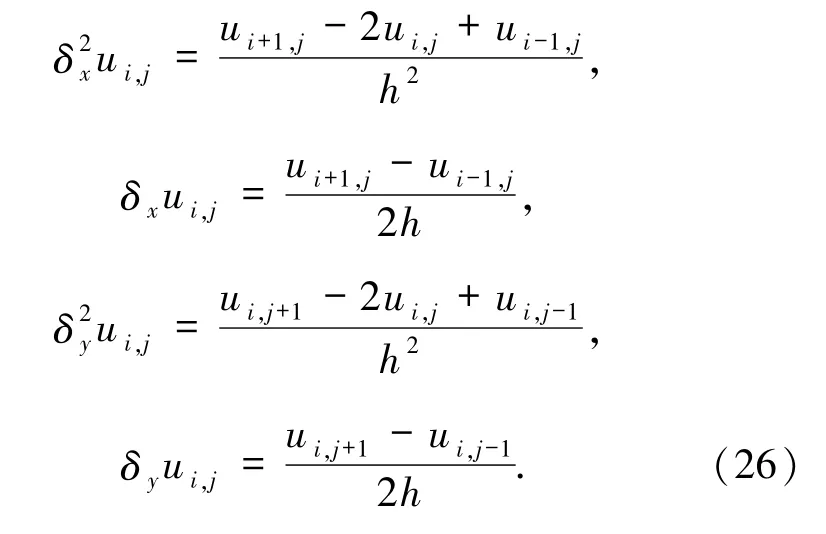
将(26)式代入(25)式进行离散:
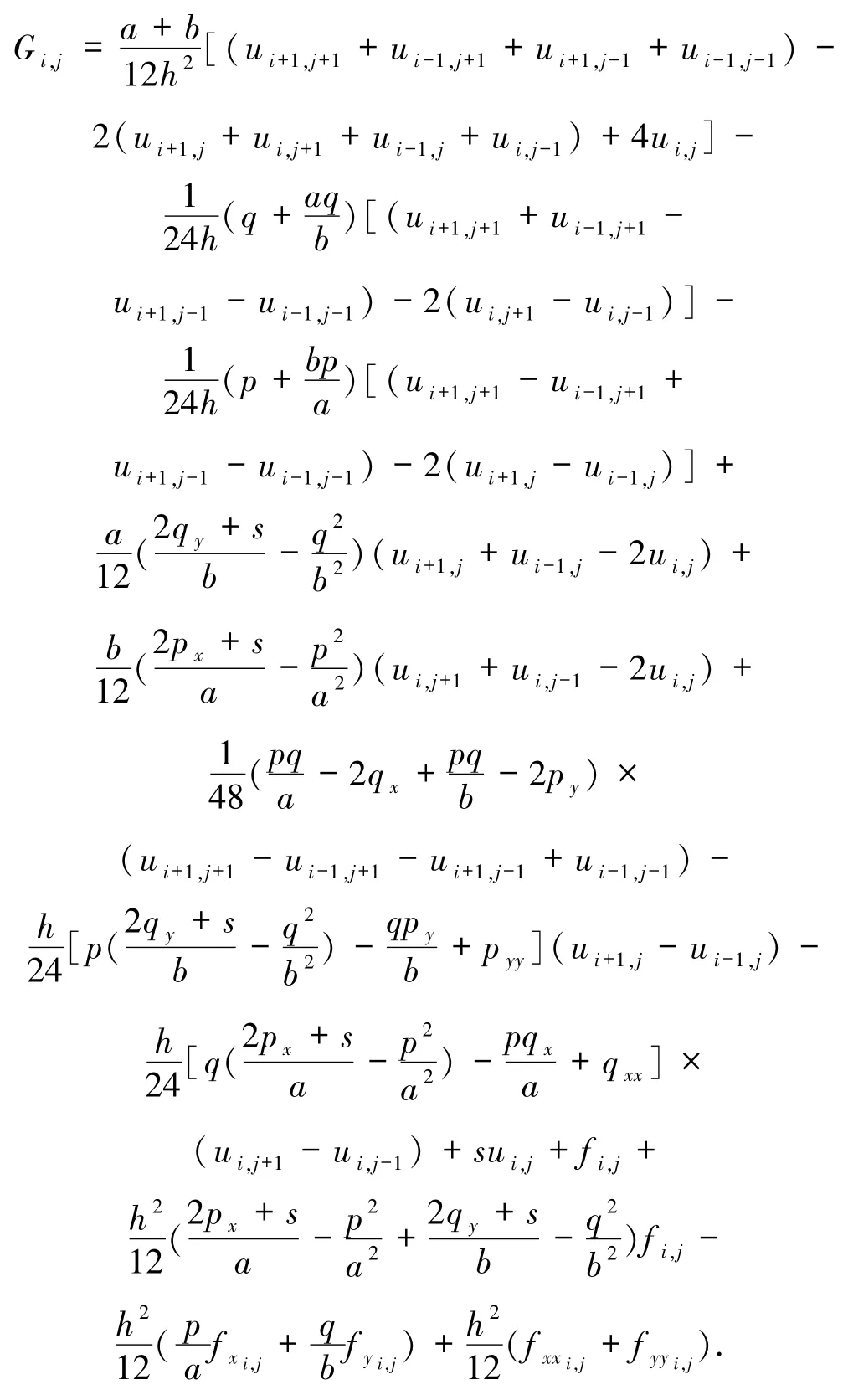
整理可得(15)式的离散格式,即为本文格式:
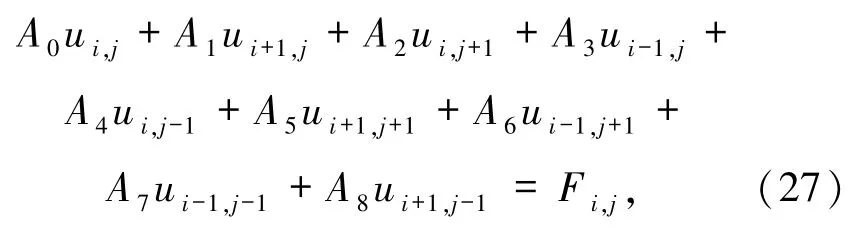
其中
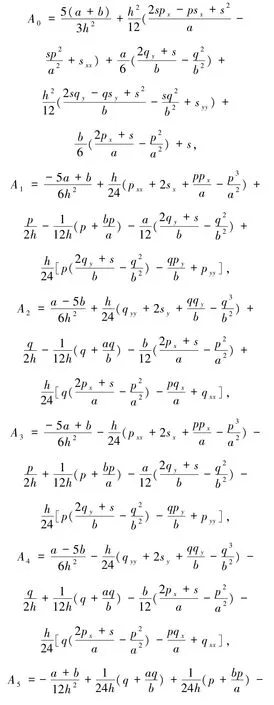
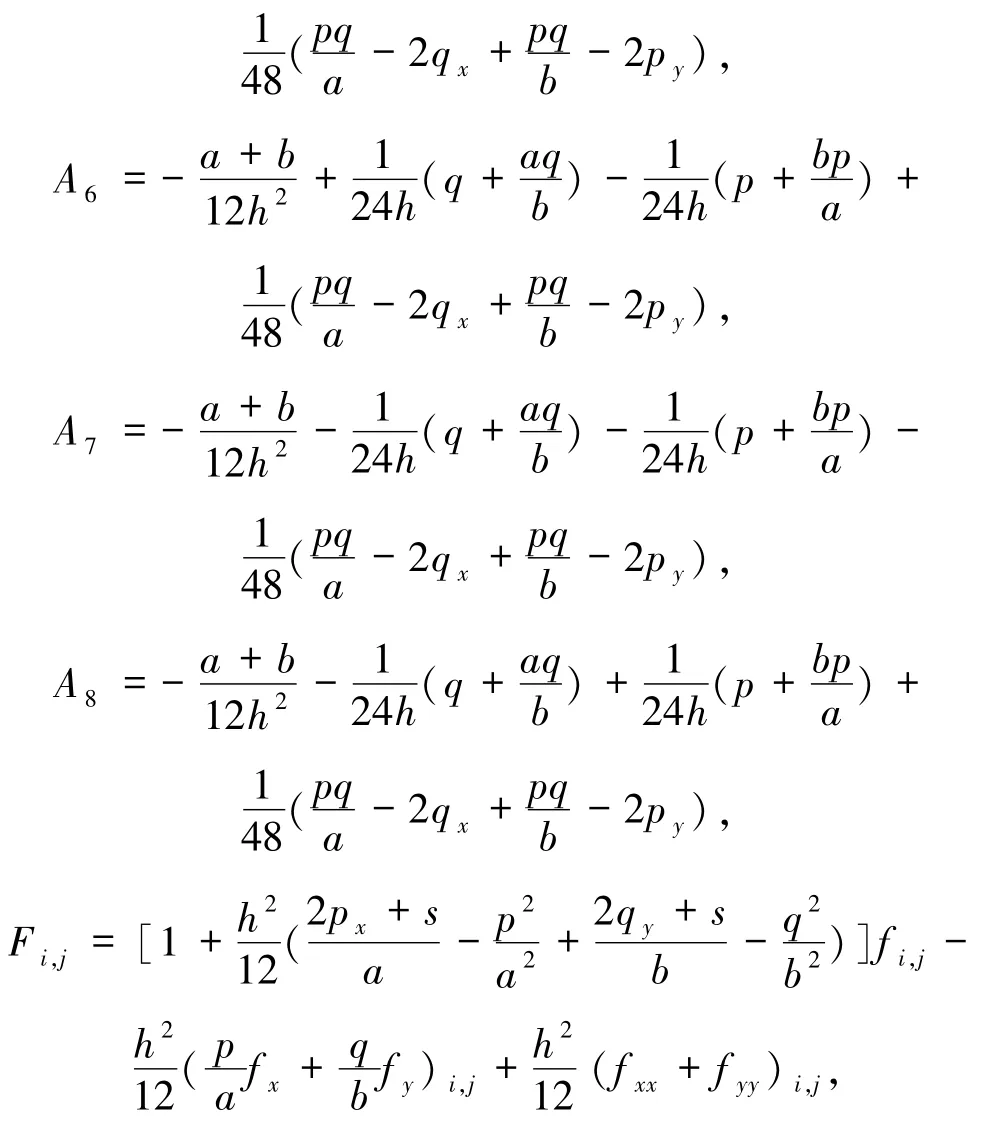
其中,A0,A1,…,A8中的函数p、q、s及其导数均在(i,j)点处取值.关于其一阶和二阶导数项的计算,均采用中心差分公式进行计算.
由推导过程可知,该格式的截断误差为O(h4),即格式(27)在空间上可达四阶精度.另外,注意到本文二维格式只用到9个网格点,故所得格式为紧致格式.
4 数值算例
为了验证本文一维和二维格式的精确性和有效性,现将以下有精确解的数值算例分别与MHOC格式[3]、Chen格式[5]、HOC格式[7]和FOC格式[8]的最大绝对误差的数值结果进行比较.其中,将一维和二维问题的最大绝对误差和收敛阶定义如下:
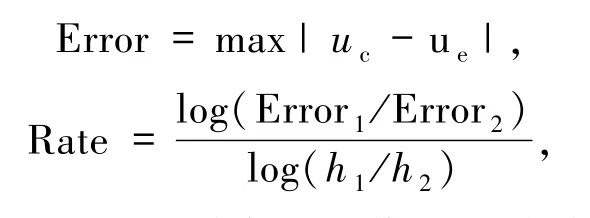
式中的uc和ue分别代表数值解和精确解,h1和h2代表不同空间步长,Error1和Error2分别对应步长为h1和h2时的最大绝对误差.
问题1[3]
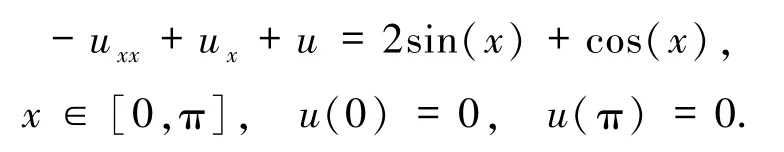
该问题的精确解为
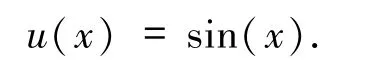
问题2[8]
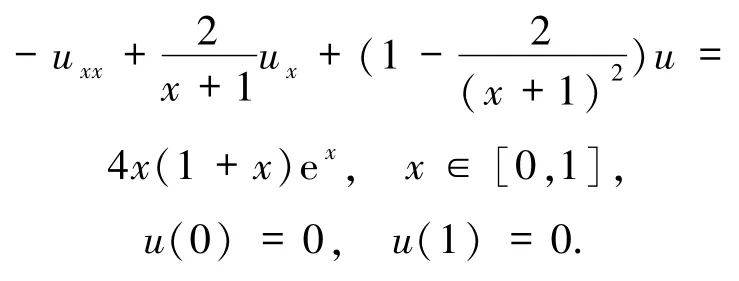
该问题的精确解为
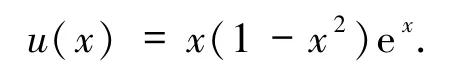
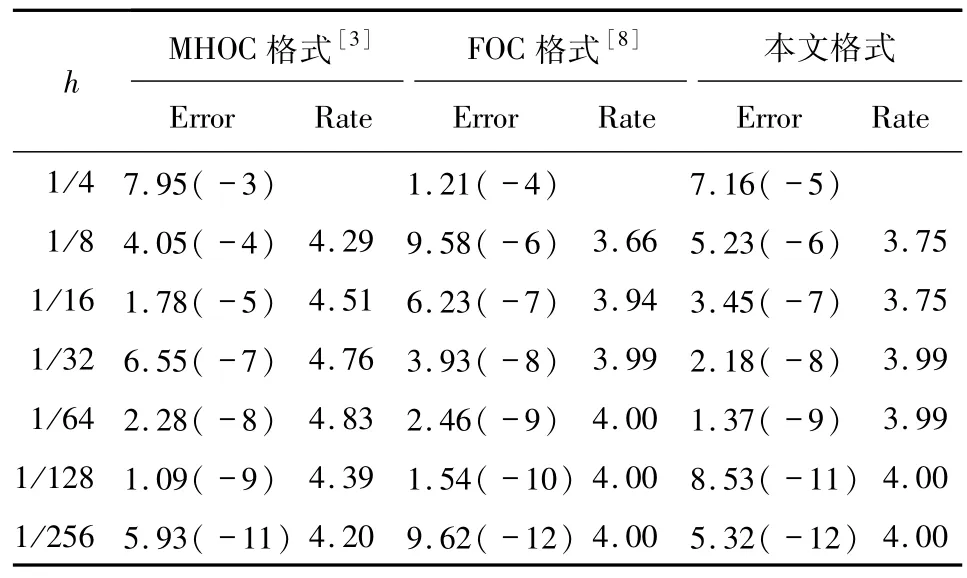
表2 问题2的最大绝对误差和收敛阶Tab.2 The maximum absolute error and convergence rate for Problem 2
问题3[7]
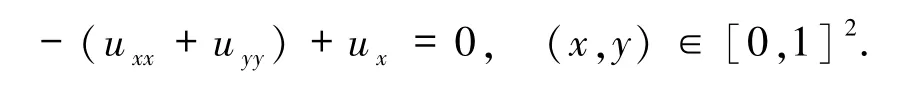
该问题的精确解为
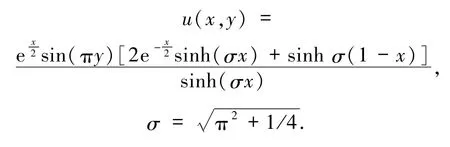
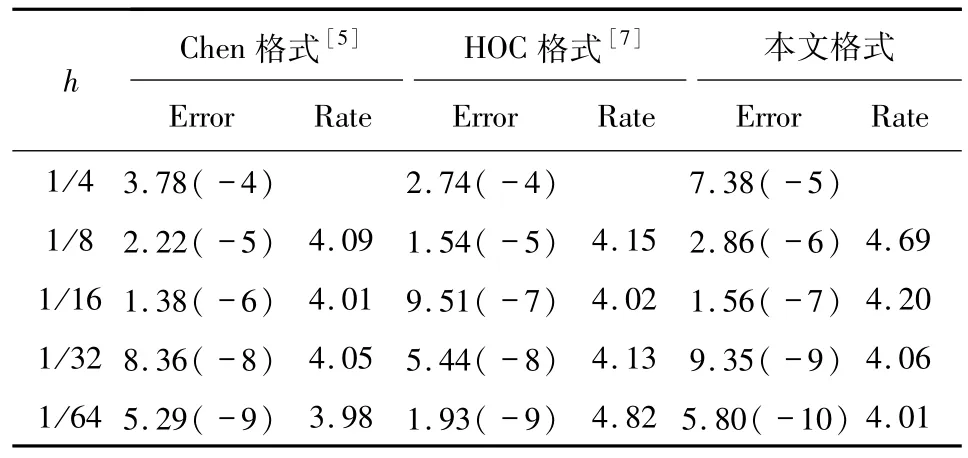
表3 问题3的最大绝对误差和收敛阶Tab.3 The maximum absolute error and convergence rate for Problem 3
问题4
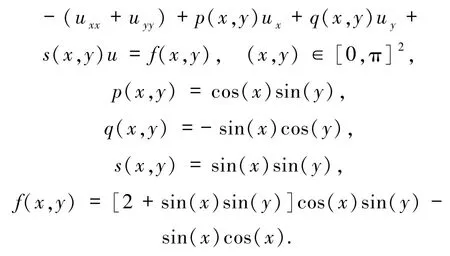
该问题的精确解为
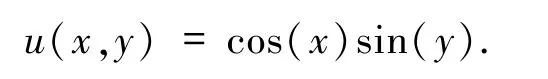
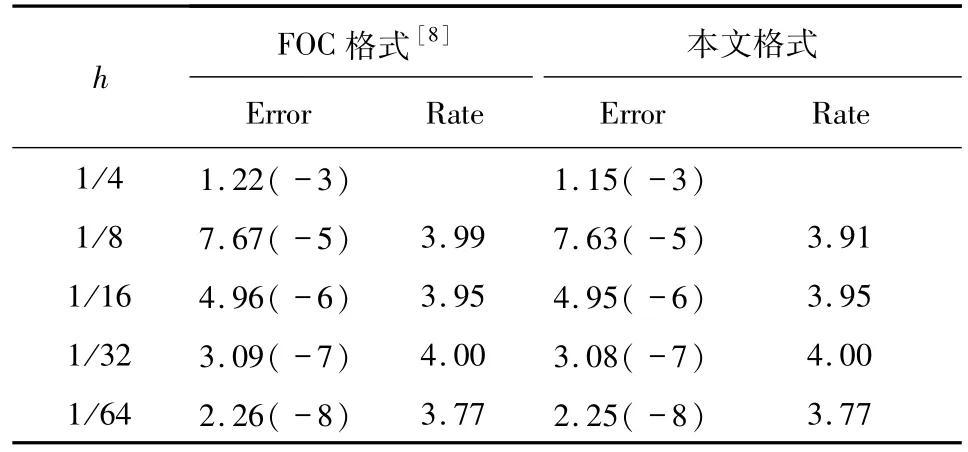
表4 问题4的最大绝对误差和收敛阶Tab.4 The maximum absolute error and convergence rate for Problem 4
表1~4列出了针对一维问题和二维问题1~4的4种格式在不同h下的最大绝对误差和收敛阶.不难发现,尽管以上4种格式的精度基本上都达到了四阶,但是本文计算所得的最大绝对误差要更小些,即本文格式的计算结果更接近于精确解,也具有更高的计算精度.需要说明的是,对于MHOC格式[3]、Chen格式[5]、HOC格式[7]和FOC格式[8]的计算结果,采用了Phoebe Solver软件进行计算得到.Phoebe Solver软件为Web版,网址为www.phoebesolver.com.对于问题4没有采用Chen格式[5]和HOC格式[7]计算是因为该问题是对流扩散反应方程,而这2篇文献中的方程模型为对流扩散方程,不包括反应项.因此,这2篇文献所提格式不适用于该问题的求解.
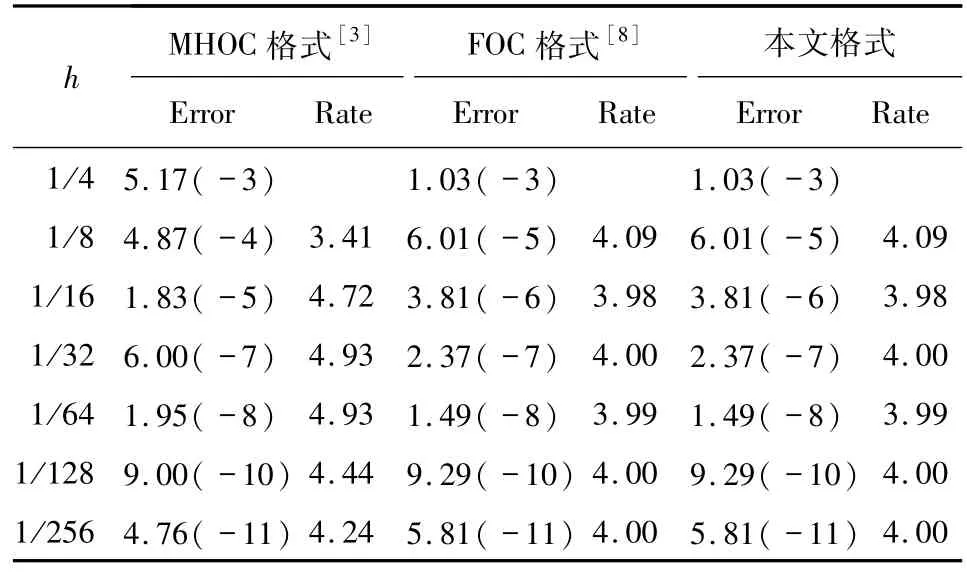
表1 问题1的最大绝对误差和收敛阶Tab.1 The maximum absolute error and convergence rate for Problem 1
5 结论
本文首先针对方程(1)提出了一种新的紧致差分格式,具有四阶精度,即在空间上采取泰勒级数展开法和截断误差余项修正法,先利用一阶导数项来表示由原方程得到的未知函数的二阶导数项,再表示出误差余项中的三阶和四阶导数项,最终得到了一个三点四阶的紧致差分格式,格式对应的三对角线型方程组可采用追赶法进行求解.接下来,对本文格式的耗散误差和色散误差进行了分析,与文献中格式的对比结果表明本文格式具有更小的耗散误差.然后将该方法推广到二维,得到了求解二维对流扩散反应方程的一种具有四阶精度的紧致差分格式.最后给出了数值实验,通过与文献中格式数值结果的比较发现本文格式具有更小的计算误差和更高的计算精度.
致谢宁夏自治区重点研发项目(2018BEE03007)和宁夏大学研究生创新项目(GIP2019010)对本文给予了资助,谨致谢意.

