折叠交叉立方体的3-额外边连通度

蔡学鹏， 徐刚刚， 史 伟

（新疆农业大学 数理学院，新疆 乌鲁木齐830052）

众所周知，互连网络在并行计算及通信系统中发挥着重要作用.一个网络的拓扑结构在数学上通常被抽象的模型化为一个图G＝（V（G），E（G）），其中V（G）是图G的顶点集，表示网络处理器的集合；E（G）是图G的边集，表示网络的通信链路集.本文中术语图和网络可以互换使用，且所有的图都认为是无向的、简单的和连通的.对于未说明的图论符号和术语，可参考文献［1-2］.

设G＝（V（G），E（G））是一个图，则对于图G中任意顶点u∈V（G），设集合

和

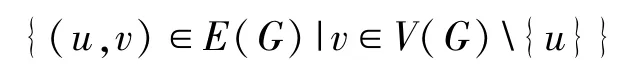
分别表示顶点u的邻点集和邻边集，记为NG（u）和NEG（u）.d G（u）＝ ｜NG（u）｜称为图G中顶点u的度.对于图G的子图K，设

和

分别表示子图K在G中的邻点集和子图K在G中的邻边集.设Kr，s＝ （V1∪V2，E）表示一个完全二部图，其中V1和V2分别是由r个点和s个点构成的不交点集.Kr，s的点集V（Kr，s）＝V1∪V2，边集E＝｛（u，v）｜u∈V1，v∈V2｝.Pn＝ 〈u1，u2，…，u n〉表示图G中一条具有n个顶点和n－1条边的路，Cn表示具有n个顶点的圈.

图G的经典连通度κ（G）和边连通度λ（G）是衡量网络可靠性和容错性的2个重要参数［3］.连通度κ（G）和边连通度λ（G）越大，网络的可靠性就越高，但也有明显的不足之处.比如，在互连网络的实际应用中，与一个处理器相连接的所有处理器（链路）同时发生故障可能性较低，所以这2个参数衡量网络可靠性和容错性是不精确的.为克服这些不足，可以通过对G-S的每一个分支强加一些限制条件来推广图G的经典连通度（边连通度），这里S⊂V（G）（S⊂E（G））.

设P是图G所具有的一种性质.Harary［4］首先提出图G的条件连通度（边连通度）概念.如果G中存在某种点子集（边子集），使得G删除这种点子集（边子集）后得到的图不连通且每个连通分支都具有性质P，则所有这种点子集（边子集）中基数最小的点子集（边子集）的基数称为图G的条件连通度（边连通度），记为 κ（G：P）（λ（G：P））.随后，Fàbrega等［5-6］研究了下面所述的一种条件连通度（边连通度）.

设S⊂V（G）（S⊂E（G））且g是一个非负整数，若G-S不连通且G-S的每个连通分支中至少有g＋1个顶点，则称S是G的一个Rg-割（Rg-边割）.如果G存在Rg-割（Rg-边割），则G中基数最小的Rg-割（Rg-边割）的基数称为G的g-额外连通度（g-额外边连通度），记为 κg（G）（λg（G））.明显的，如果G不是完全图，则 κ0（G）＝κ（G）且

因此，g-额外连通度（g-额外边连通度）可以认为是经典连通度（边连通度）的一种推广形式，并且它能更加精确地衡量大型并行处理系统的可靠性和容错性.网络（图）的g-额外连通度（g-额外边连通度）［7-22］已被许多学者研究.

在平行计算系统中，n维交叉立方体CQ［23-25］

n和n维折叠超立方体FQn［26］是最重要且最流行的2个互连网络.基于交叉立方体和折叠超立方体，Zhang［27］介绍了n维折叠交叉立方体，记作FCQn.FCQn具有许多重要的特性，比如短的直径、短的平均距离和非常低的消息流量密度.Pai等［28］研究了FCQn的点传递性.对于FCQn的详细结果可参看文献［7，28-30］.

Adhikari等［29］证明 κ（FCQn）＝ κ0（FCQn）＝λ（FCQn）＝ λ0（FCQn）＝n＋1，n≥2.Cai等［7，30］分别确定了

下面将证明

1 预备知识

定义1.1设x＝x1x0和y＝y1y0是2个二进制字符串，如果

则称x和y是相关的，记作x～y；否则，x和y是不相关的，记作x

n维交叉立方体CQn的顶点集

它的递归定义如下.

定义1.2［23］CQ1是2个顶点标为0和1的完全图.当n≥2时，CQn是由2个n－1维子交叉立方体中的每个顶点最左面的第一个字符分别是0和1.和中的2个顶点u＝0u n－2…u0和v＝1vn－2…v0是相邻的，当且仅当

1）如果n是偶数时，则u n－2＝vn－2；

通过以上定义，可得下面的推论.

推论1.1［23］CQn中的2个顶点

是相邻的，当且仅当存在整数l，1≤l≤n，满足下面4个条件：

由定义可知，CQn是有2n个顶点和n2n－1条边的n－正则图.当n≥2时，CQn可分解成2个子交叉立方体是由点集｛iu n－2…u0｝，i∈｛0，1｝诱导的CQn的子图.和是由一个完美匹配相连.

下面给出n维折叠交叉立方体的定义.

定义1.3［29］n维折叠交叉立方体，记为FCQn.它是由交叉立方体CQn中的任意2个互补的点x＝x n－1x n－2…x0和增加一条边后得到的，其中这些新增加的边称为FCQn的补边，它们构成的集合记为中的边称为FCQn的交叉边.

图1表示CQ3和FCQ3的图.由定义可知，FCQn是有2n个顶点和（n＋1）2n－1条边的（n＋1）-正则图.

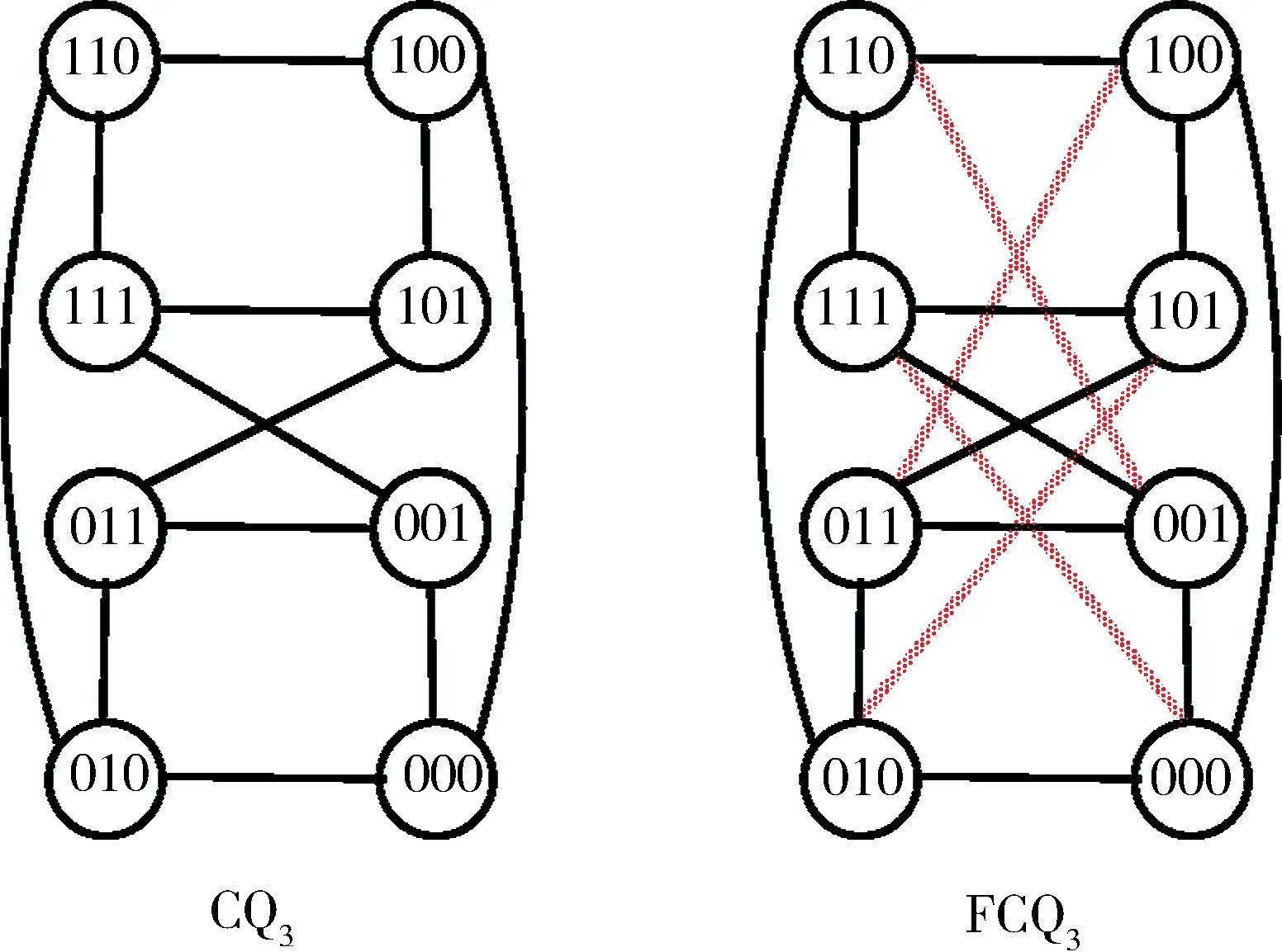
图1 CQ 3和FCQ 3Fig.1 CQ 3 and FCQ 3

对于FCQn＋1，如果FCQn＋1中的2个顶点是通过交叉边相邻的，且它们最左面的第i（0≤i≤n）个字符是不同的，则称它们是沿着维数i相邻，也称v是u的i-邻点，记作v＝u i.由定义可知，u ij是u i的j-邻点.明显地，u ii＝u.FCQn＋1－中的边（u，u i）定义为顶点u的i-边，记作ei（u）.设

表示与顶点u关联的补边.

由定义1.3可知，FCQn＋1（n≥2）可以分解成2个子交叉立方体是由点集｛iu n－1…u0｝，i∈｛0，1｝诱导的FCQn＋1的子图.和之间通过2个完美匹配和M0是连通的，其中设

引理1.1［25］κ1（CQn）＝ λ1（CQn）＝2n－2，n≥3.

引理1.2［19］κ2（CQn）＝ λ2（CQn）＝3n－4，n≥4.

引理1.3［3］CQn（n≥3）中不含3长圈.

文献［7］中，证明了下面的引理.

引理1.4［7］设u和v是CQn中2个不同的顶点，则｜NCQn（u）∩NCQn（v）｜≤2.

引理1.5［7］FCQn（n≥4）中不含3长圈.

引理1.6［7］设u和v是FCQn中2个不同的顶点，则｜NFCQn（u）∩NFCQn（v）｜≤2.

由CQn的定义可知，CQn中包含C4、P4和K1，3.通过引理1.3和1.4，很容易得到下面3个引理.

引理1.7设C4是CQn（n≥2）中的一个4长圈，那么｜NECQn（C4）｜＝4n－8.

引理1.8设P4是CQn（n≥3）中的一个4长路，那么｜NECQn（P4）｜＝4n－6.

引理1.9设K1，3是CQn（n≥3）中的子图，那么｜NECQn（K1，3）｜＝4n－6.

方便起见，下面的讨论中考虑FCQn＋1.

通过引理1.5和1.6，可得下面的引理.

引理1.10设C4是FCQn＋1（n≥2）中的一个4长圈，那么｜NEFCQn＋1（C4）｜＝4n.

2 主要结论

引理2.1设A是由CQn（n≥3）中的4个顶点诱导的子图.若u∈V（CQn－A），则｜NA（u）｜≤2.

证明很容易知道，A与P4同构，或者A与C4同构，或者A与K1，3同构.通过反证法，假设｜NA（u）｜≥3.因此，要么CQn中包含3长圈，要么CQn中的任意2个不同顶点的公共邻点个数至少是3个，这与引理1.5和1.6的结论矛盾.

引理2.2设K⊂E（CQn）且｜K｜≤2n－2（n≥4），则CQn－K满足下面3种情形之一：

1）CQn－K是连通的；

2）CQn－K有2个分支，其中一个分支是一个孤立顶点；

3）CQn－K有2个分支，其中一个分支是一条孤立边.

证明下面的讨论假设n≥4.

如果CQn－K是连通的，则情形1）成立.现在可假设CQn-K是不连通的.因为

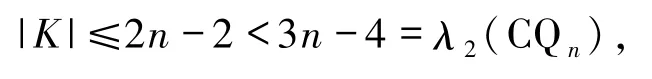
所以CQn－K中至少包含一个孤立顶点或者一条孤立边.另外，因为CQn中至少移除2n－1条边后才能产生2个孤立顶点并且又因｜K｜≤2n－2，所以CQn－K中至多包含一个孤立顶点.相反地，因为CQn中至少移除3n－4条边后才能产生一个至少有3个顶点的孤立顶点集，且｜K｜≤2n－2＜3n－4，所以CQn－K要么包含唯一一个孤立顶点，要么包含唯一一条孤立边.下面考虑2种情形.

情形1 设u是CQn－K中唯一一个孤立顶点.因为

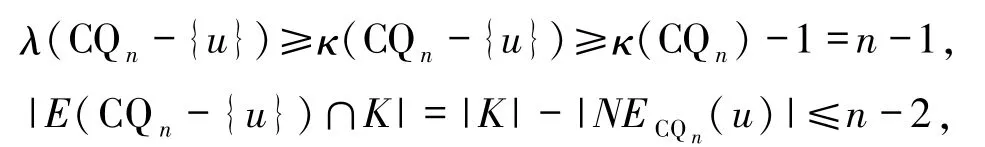
所以CQn－K－｛u｝是连通的.因此，可知引理中情形2）成立.

情形2 设e＝（u，v）是CQn－K中唯一一条孤立边.因为

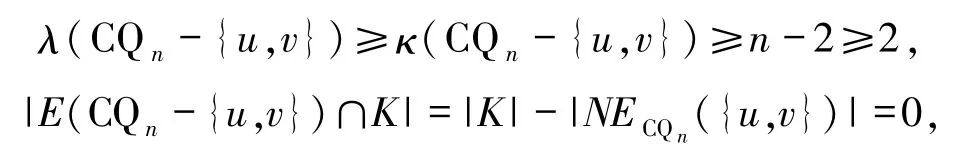
所以CQn－K－｛u｝是连通的.因此，可知引理中情形3）成立.

引理2.3设K⊂E（FCQn＋1）（n≥3），令FCQn＋1＝L⊕R，于是

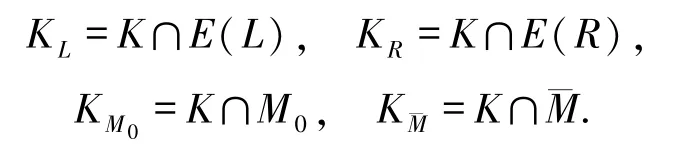
如果｜K｜≤4n－1且FCQn＋1－K中不含任何孤立顶点、孤立P2和孤立P3，那么L－KL（R－KR）中的每一个顶点都与R－KR（L－KL）中的某个点连通.

证明设u∈V（L－KL）.若e0（u）∉KM0或者（u）∉K，则结论成立；否则，e0（u）∈KM0且（u）∈K.因为FCQn－K中不含孤立顶点，所以存在一个顶点v∈V（L－KL），使得v是u的邻点.如果e0（v）∉KM0或者（v）∉K，则结论成立；否则，e0（v）∈KM0且（v）∈K.因为FCQn－K中不含孤立P2，所以存在一个顶点w∈V（L－KL），使得w是u或者v的邻点.如果e0（w）∉KM0或者（w）∉K，则结论成立；否则，e0（w）∈KM0且（w）∈K.由于FCQn－K中不含孤立P3，所以存在一个顶点z∈V（L－KL），使得z是u或者v或者w的邻点.如果e0（z）∉KM0或者（z）∉K，则结论成立；否则，可设e0（z）∈KM0且（z）∈K.方便起见，令A＝ ｛u，v，w，z｝，K′＝ ｛e0（u），（u），e0（v），（v），e0（w），（w），e0（z），（z）｝.

下面证明FCQn＋1－K′中存在｜NEL（A）｜条两两边不交的连接A与R的路.设y∈NL（A）.由引理2.1可知，A与顶点y关联的邻边至多有2条.如果与y关联的A的邻边只有一条（可设为e），则可选择〈e，e0（y）〉作为连接A与R的路；否则，设e1和e2是与y关联的A的2条邻边.在这种情形下，可分别选择〈e1，e0（y）〉和〈e2，e0（y）〉作为连接A与R的路.通过考虑NL（A）中的每一个顶点y.由引理1.7～1.9可知，FCQn＋1－K′中存在

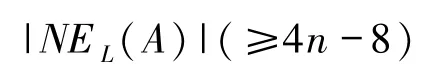
条两两边不交的连接A与R的路.但是，因为这些路至多包含K中的

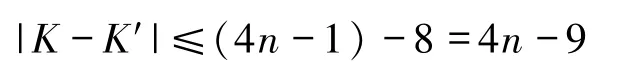
条边，所以至少存在一条连接u到R－KR中某个顶点的路.同理，可证明R－KR中的每一个顶点都与L－KL中的某个顶点连通.

定理2.1λ3（FCQn＋1）＝4n，n≥4.

证明假设n≥4，设C4是FCQn＋1中的一个4长圈.通过引理1.10可得｜NEFCQn＋1（C4）｜＝4n.令Y＝FCQn＋1－V（C4），因为 ｜V（C4）｜＝4且κ（FCQn＋1）＝n＋2≥6，所以Y是连通的.进一步，

所以NEFCQn＋1（C4）是FCQn＋1中的一个R3-边割，即λ3（FCQn＋1）≤4n.

下面证明 λ3（FCQn＋1）≥4n，n≥4.设K⊂E（CQn）使得｜K｜＝4n－1，且FCQn＋1－K中不含任何孤立顶点、孤立P2和孤立P3.为了证明λ3（FCQn＋1）≥4n，只需证明FCQn＋1－K是连通的，设FCQn＋1＝L⊕R.

设Mi（i＝1，2…，n）是FCQn＋1－ （M0∪）中的一边集且Mi中每条边的2个顶点最左面的第i个字符是不同的，于是M0，M1，…，Mn和形成了E（FCQn＋1）的一个划分.对每个i∈｛0，1，…，n｝，如果有｜Mi∩K｜≤2且｜∩K｜≤2，则

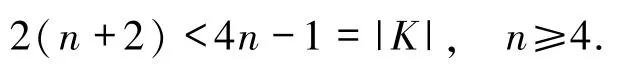
因此，存在某个i∈｛0，1，…，n｝，使得｜Mi∩K｜≥3或者另外，对FCQn＋1的顶点重新标号使得

方便起见，设

因此

不失一般性，假设｜KL｜≤｜KR｜，于是有

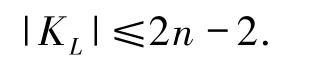
由引理2.2可知，L－KL满足下面3种情形之一：

1）L－KL是连通的；

2）L－KL有2个分支，其中一个分支是一个孤立顶点；

3）L－KL有2个分支，其中一个分支是一条孤立边.

情形1L－KL是连通的.通过引理2.3，容易得到R－KR中的每一个顶点与L－KL中的某个顶点是连通的.因此，FCQn＋1－K是连通的.

情形2L－KL有2个分支，其中一个分支是一个孤立顶点.设u是L－KL中一个孤立的顶点.接下来证明FCQn＋1－K中u与L－KL－｛u｝是连通的.注意到｜KL｜≥｜NEL（u）｜＝n.因为FCQn＋1－K中不含任何孤立点，所以e0＝（u，u0）∉KM0或者考虑下面2种情形.

根据引理2.3相似的讨论方法，可得

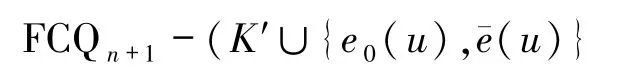
中存在｜NE R（A）｜＝2（n－1）＋n＝3n－2条两两边不交的连接A与L－KL－｛u｝的路，但是这些路至多包含K中的

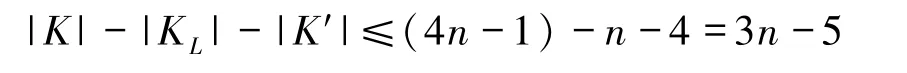
条边.因此，FCQn＋1－K中u与L－KL－｛u｝是连通的.

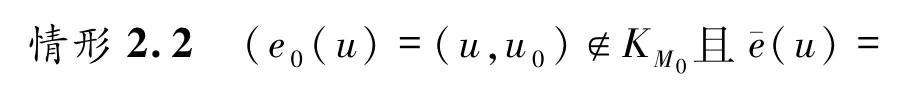
根据引理2.3的证明中相似的讨论方法，可得FCQn＋1－（K′∪｛e0（u）｝）中存在

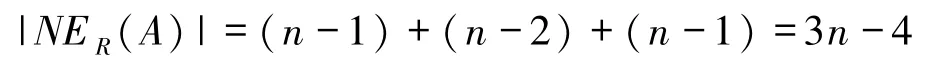
条两两边不交的连接A与L－KL－｛u｝的路，但是这些路至多包含K中的

条边.因此，FCQn＋1－K中u与L－KL－｛u｝是连通的.

情形3L－KL有2个分支，其中一个分支是一条孤立边.设e＝（u，v）是L－KL中一个孤立的边，下面证明FCQn＋1－K中边e与L－KL－｛u，v｝是连通的.因为

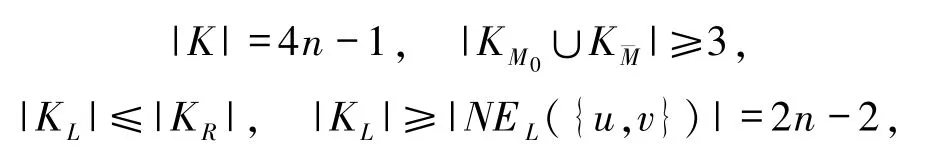
所以导致｜KL｜＝ ｜KR｜＝2n－2且｜KM0∪K｜＝3.现在可考虑两两边不交的路的集合B＝｛〈e0（u），中的每一条路都是连接e到L－KL－｛u，v｝.因为构成B中每一条路的边都属又因为｜B｜＝4且｜KM0∪K｜＝3，所以B中存在一条路P使得e通过P与L－KL－｛u，v｝连通.

3 结束语

本文在折叠交叉立方体网络经典连通度和超连通度的基础上，进一步研究3-额外边连通度，证明了当n≥5时，λ3（FCQn）＝4n－4.也就是说，FCQn至少删除4n－4条边，才能得到不包含孤立顶点、孤立P2和孤立P3的非连通图.FCQn的经典边连通度是n＋1.由此可知，3-额外边连通度几乎是经典边连通度的4倍，这使得FCQn可靠性的度量更加精确.因此，3-额外边连通度比经典边连通度更适合评价大规模折叠交叉立方体网络的可靠性.另一方面，经典边连通度假定折叠交叉立方体网络的任一顶点的所有邻边都可能同时故障，这种情况几乎不可能发生.然而3-额外边连通度假定折叠交叉立方体网络的任一顶点的部分邻边不能同时故障，这更符合实际情况.因此，在评价折叠交叉立方体网络的可靠性时，3-额外边连通度比经典边连通度更具优势性.