相关熵的降噪机理及其在轴承故障诊断中的应用

李辉

(天津职业技术师范大学 机械工程学院，天津 300222)

机电设备故障产生的振动信号具有明显的非高斯和非线性等特征，相关分析、功率谱估计等基于信号二阶统计量的传统方法在处理这类信号时往往不能取得满意的效果[1-3]。基于信号高阶统计量的双谱、高阶谱分析则在非线性、非高斯信号处理方面有着独特优势，但高阶统计量(Higher Order Statistics，HOS)存在计算方法复杂且计算量大的缺点[4-5]。分数低阶统计量[6-9]( Fractional Lower Order Statistics，FLOS)尽管能在一定程度上消除非高斯噪声的影响，但却过度依赖被分析信号噪声Alpha值的先验知识，噪声抑制能力受到极大地限制。相关熵[10-13]是一种分析高斯噪声和非高斯噪声的高效方法，已成功应用于通信信号检测、雷达回波信号检测、波达方向估计、信号滤波和时延估计等领域，且取得了较好的分析效果[14-19]。虽然相关熵已成功应用于雷达、通信等技术领域，但在机电设备故障诊断领域的应用才刚刚起步，因此，将相关熵与其他信号处理方法相结合，开展基于相关熵技术的机电设备故障特征提取与诊断，具有很重要的理论创新和工程应用价值[20]。

近年来，基于振动信号分析的旋转机械故障诊断方法在信号降噪、故障特征提取等方面取得了较好的效果，其中的循环平稳分析和谱峭度方法由于其高效性和稳健性引起了研究者的瞩目[21-22]。但传统基于信号二阶统计量的循环平稳信号分析在处理强高斯噪声和非高斯噪声时会造成性能衰退，甚至失效。因此，针对传统相关函数和谱相关密度难以有效处理强非高斯噪声干扰的问题，提出了基于循环平稳相关熵的故障诊断方法，从理论分析、几何图解和信号仿真等几个方面系统阐释了相关熵的降噪机理，并通过试验验证循环平稳相关熵在滚动轴承故障诊断中有效处理染噪信号的能力。

1 相关熵及循环平稳相关熵

1.1 相关熵的估计

对于任意2个实随机变量x,y，其互相关熵可定义为

Vσ(x,y)=E[κσ(x-y)]，

(1)

式中：κσ(·)为满足Mercer条件的核函数；σ为核函数的核长。σ定义了随机变量x和y相似性的特征长度尺度，即权重空间视角下特征空间映射前后随机变量x与y之间距离的比例。

对于实信号x(t)∈R，时变自相关熵可定义为

(2)

κσ(·)一般采用高斯核函数，其解析式为

κσ[x(t),x(t+τ)]=

(3)

式中：·为一种范数算子。

在实际应用中，假设x(i)是长度为N的观测样本，其自相关熵(下文统称为相关熵)的无偏估计可表示为

(4)

式中：m为时延的采样点数，m=0,1,2,…,N-1。由(4)式估计的相关熵是一个正定的对称函数。

V=

(5)

上述相关熵矩阵V是N×N的正定、对称矩阵。

1.2 循环平稳相关熵

(6)

(7)

(8)

1.3 循环平稳相关熵谱密度计算步骤

在实际应用中可通过以下步骤计算信号的循环平稳相关熵谱密度：

1)根据(4)式计算信号的相关熵。

2)根据(5)式计算信号的相关熵矩阵V。

3)计算相关熵矩阵V各行的傅里叶变换，得到信号循环平稳相关熵函数矩阵R。

4)计算信号循环平稳相关熵函数矩阵R各列的傅里叶变换，得到信号的循环平稳相关熵谱密度函数矩阵S。

2 相关熵的降噪机理

2.1 理论分析

将(2)式表示的时变相关熵展开为泰勒级数形式，即

x(t+τ)]2n}。

(9)

由(9)式可知：

3)可通过调整σ来控制高斯核函数曲线的形状，σ的引入使相关熵函数和循环平稳相关熵谱密度对于具有不同统计特性(概率密度)的信号都具有适应性，因此，可根据分析信号的性质和目的选择合适的σ。

2.2 几何图解

不失一般性，假设有2个随机变量X和Y，则可由(1)式表示的互相关熵定义相关熵诱导的度量[12](Correntropy Induced Metric，CIM)，即

(10)

SCIM(X,Y)是对称函数，当核函数为平移不变核函数(如高斯核函数)时，SCIM(X,Y)也是平移不变的。SCIM(X,Y)是随机变量X与Y之间相似性的一种度量，SCIM(X,Y)越大，表示X与Y越不相似，反之，SCIM(X,Y)越小，表示X与Y越相似。为透彻理解SCIM(X,Y)蕴含的内在规律，绘制了σ=1时SCIM(X,0)的三维图(图1)，其等高线图如图2所示。

图1 SCIM(X,0)三维图(σ=1)Fig.1 3D diagram of SCIM(X,0)(σ=1)

图2 SCIM(X,0)等高线图(σ=1)Fig.2 Contour map of SCIM(X,0)(σ=1)

由图1、图2可知，不同区域的SCIM(X,0)具有不同的形状，根据SCIM(X,0)的形状和性质，可以将SCIM(X,0)分为3个区域：

1)欧几里得区，即图2中心圆形区域部分。当空间中两点间距离很近时，SCIM相当于L2范数。

2)过渡区，即图2中近似方形区域部分。当空间中两点间距离比较近时，SCIM相当于L1范数。

3)矫正区，即图2中以4个角为中心的扇形区域部分。当空间中两点间距离很远时，SCIM相当于L0范数，在该区域，随着两点间距离的继续增大，SCIM的值将趋于饱和(不变)，因此，该区域是信号异常值的免疫区。

综上可知，SCIM可以作为2个随机变量相似性的度量工具：SCIM越小，表明2个随机变量越相似；SCIM=0，2个随机变量完全相同；SCIM越大，2个随机变量的差异越大。

当信号中含有幅值较大的异常值时，其SCIM值将位于矫正区，而矫正区是信号异常值的免疫区，SCIM将趋于不变，异常值对SCIM几乎没有影响，因此，相关熵能有效抑制信号中的异常值，对于随机脉冲噪声具有很强的免疫力，因而基于相关熵的信号分析具有很好的鲁棒性。

为对比核长σ对相关熵的影响，绘制了σ=0.1时SCIM(X,0)的三维图及其等高线图，结果如图3、图4所示。对比图1—图4可知：σ越大，欧几里得区范围越大，矫正区范围越小；σ越小，欧几里得区范围越小，矫正区范围越大；离原点很远的点，其SCIM表现为各向异性，即距离与方向有关。

图3 SCIM(X,0)三维图(σ=0.1)Fig.3 3D diagram of SCIM(X,0)(σ=0.1)

图4 SCIM(X,0)等高线图(σ=0.1)Fig.4 Contour map of SCIM(X,0)(σ=0.1)

由此可以看出：核长σ对于空间中两点间距离的度量具有重大影响，当σ值较大时，欧几里得区范围较大，相当于传统的二阶统计量适用的区域，可以对线性信号进行有效处理；当σ值较小时，欧几里得区范围较小，矫正区范围较大，相当于高阶统计量适用的区域，可以对非线性信号进行有效处理。因此，在实际应用时，可以根据被处理信号的性质，选择合适的核长σ。

2.3 小结

通过以上分析可以得出以下结论：

1)相关熵是基于核函数的随机变量间局部相似性度量方法，其既考虑了随机时间信号的统计特性(概率密度)，又考虑了随机时间信号的时间结构(相关关系)，是传统相关函数的一般化和推广，在包含传统相关函数特性的基础上提高了性能。

2)相关熵不仅包含随机变量幅值的二阶矩，而且包含了随机变量幅值的高阶矩，因此能够有效刻画信号的非线性特征，有效处理非线性信号。

3)相关熵能够有效抑制高斯及非高斯噪声，基于核函数的相关熵为高斯、非高斯噪声的处理提供了一种崭新的鲁棒性解决方法。

4)相关熵利用核函数，将原特征空间线性不可分的数据映射到高维希尔伯特空间，将其转变为线性可分的数据，从而能有效刻画原特征空间数据的非线性特征。

5)相关熵利用核函数，能高效进行内积运算，节省了计算时间。

3 仿真验证

3.1 相关熵核长的影响

由高斯核函数定义的相关熵有一个自由核长参数σ，用一个余弦信号说明核长σ对相关熵的影响，并验证相关熵抑制非高斯噪声的能力。余弦信号的频率为10 Hz，采样频率为1 000 Hz，采样时间为1 s，余弦信号及其傅里叶变换如图5所示。

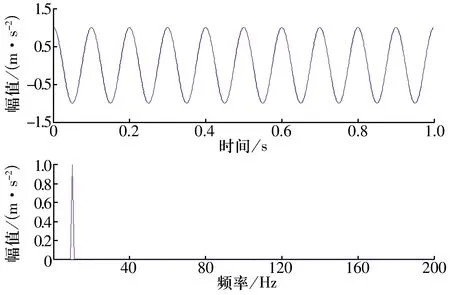
图5 仿真余弦信号及傅里叶变换Fig.5 Simulative cosine signal and its FFT

当σ取0.04，0.40，1，10时，根据(4)式计算余弦信号的相关熵及其频谱，结果如图6、图7所示，由图可知：随着σ的增大，相关熵会逐渐接近于传统的自相关函数；当σ减小时，相关熵趋向于正值，相关熵与相关函数的时域波形则完全不同；当σ趋近于0时，相关熵趋近于脉冲信号。σ的取值越小，相关熵的频谱图中包含信号频率的高次谐波成分越多，随着σ的增大，相关熵的频谱图中包含信号频率的高次谐波成分越少，例如当σ=10时，相关熵的频谱图与余弦信号的频谱图相同。综上可知，核长σ是影响相关熵中统计量成分的权重系数，与根据相关熵的泰勒展开式的理论分析相吻合，其主要原因是高斯核函数是一种非线性变换，因此，在信号处理时应根据信号的性质选取适当的核长。

图6 余弦信号的相关熵Fig.6 Correntropy for cosine signal

图7 余弦信号相关熵的傅里叶变换Fig.7 FFT of correntropy for cosine signal

为对比相关熵与传统相关函数处理非高斯噪声的性能，将Alpha分布噪声(图8a)与余弦信号进行合成，合成信号如图8b所示，其广义信噪比为-10 dB。由于强非高斯噪声的影响，从合成信号的傅里叶变换结果(图8c)中无法识别出余弦信号的频率成分。

图8 余弦信号与Alpha分布噪声合成信号及其傅里叶变换Fig.8 Composite signal of cosine signal with Alpha noise and its FFT

合成信号的自相关函数如图9所示，由图可知：自相关函数在τ=0时取得最大值，但从图中无法观察到合成信号中的周期性变化；而由于Alpha分布噪声的二阶统计量不存在，从自相关函数的傅里叶变换图中也无法识别余弦信号的频率成分；因此，传统基于二阶统计量的信号处理方法，在处理含有非高斯噪声的信号时，会造成性能衰退，甚至失效。

图9 合成信号的相关函数及其傅里叶变换Fig.9 Correlation function and FFT of composite signal

为有效识别合成信号中的频谱成分，对合成信号进行相关熵运算(σ=0.4)，结果如图10所示，由图可知：相关熵图中可以观察到明显的周期性变化，而相关熵的傅里叶变换图中存在显著的谱峰(10 Hz处)，表明相关熵能从强非高斯噪声中提取信号的周期成分。

图10 合成信号的相关熵及其傅里叶变换Fig.10 Correntropy and FFT of composite signal

3.2 循环平稳相关熵降噪性能仿真

采用一个仿真调幅信号详细解释循环平稳相关熵的降噪机理，并验证其有效抑制噪声的能力，仿真调幅信号的解析表达式为

x(t)=[1+cos(2πf0t)]cos(2πfct)+

n1(t)+n2(t)，

(11)

式中：f0为调制频率，取200 Hz；fc为载波频率，取1 000 Hz；n1(t)为零均值高斯白噪声；n2(t)为随机脉冲噪声。信号的采样频率为6 000 Hz，采样点数为600，通过该仿真调幅信号，利用循环平稳相关熵谱密度诠释循环平稳相关熵的降噪机理并验证其对高斯白噪声和随机脉冲噪声的降噪性能。

在仿真调幅信号x(t)中加入零均值高斯白噪声n1(t)，获得信噪比为-10 dB的合成信号，之后再随机加入几个幅值不等的脉冲信号以模拟随机脉冲噪声。仿真调幅信号的时域波形如图11所示，由于调幅信号完全被噪声淹没，从时域波形中已完全看不出信号的变化规律，在其傅里叶变换图中也很难识别载波频率及调制频率。

图11 仿真调幅信号的时频图Fig.11 Time-frequency diagram of simulative amplitude modulation signal

计算仿真调幅信号的循环平稳相关熵谱密度(σ=3)，结果如图12所示，由图可知：在循环频率α和谱频率f构成的双频平面内，信号的能量主要分布在f=0,α=0及f=-0.5α这3条频谱线上，其余区域循环平稳相关熵谱密度的能量为零，表明循环平稳相关熵谱具有很强的能量聚集性，其中高斯噪声的能量主要聚集在f=0及α=0这2条频谱线上；调幅信号的能量主要聚集在f=-0.5α这条频谱线上；非高斯噪声能量分散在其他区域，已被循环平稳相关熵谱有效抑制。

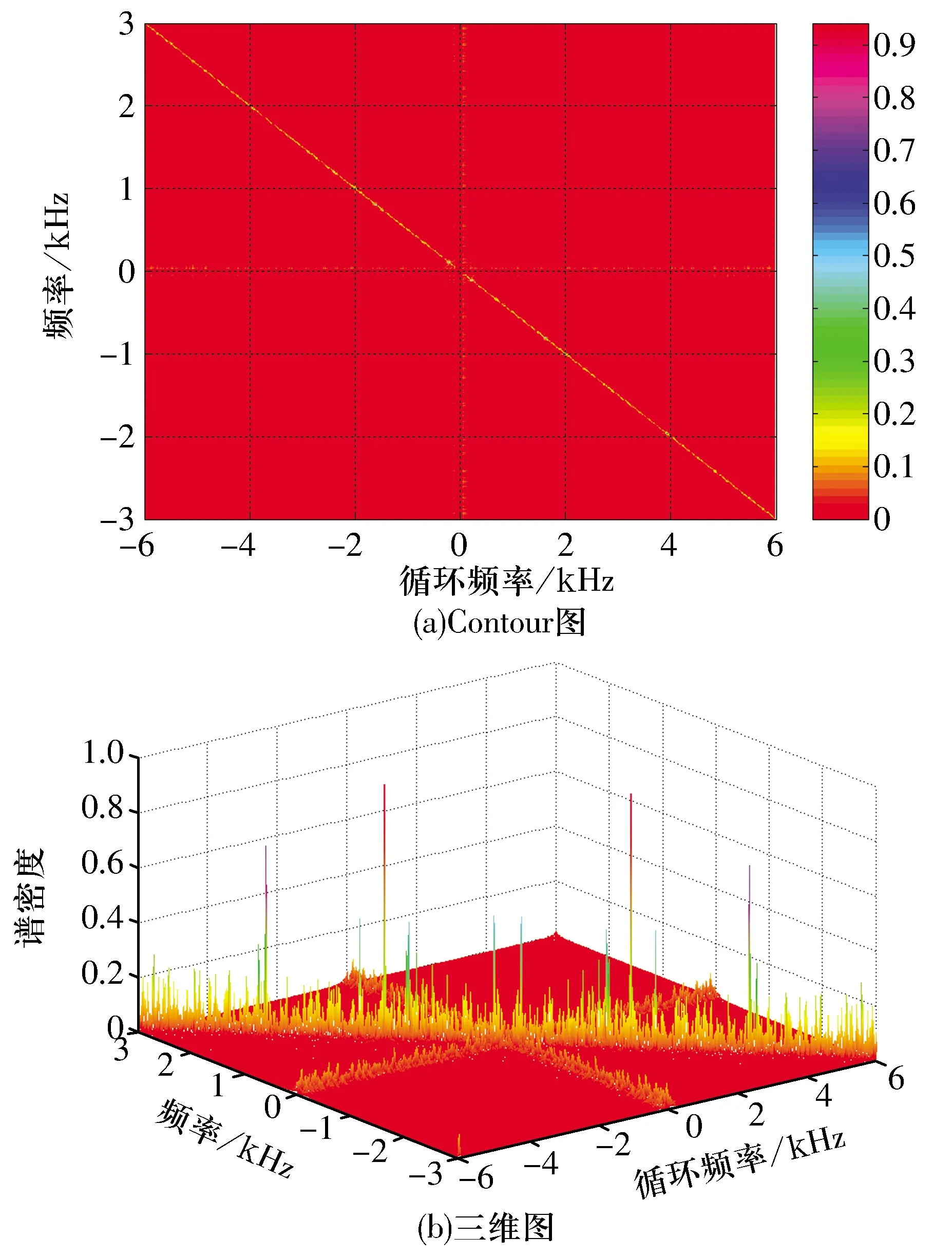
图12 仿真调幅信号循环平稳相关熵谱Fig.12 Cyclostationary correntropy spectrum of simulative amplitude modulation signal

在低频段，仿真调幅信号x(t)的循环平稳相关熵谱在α=±f0的位置存在明显的谱峰，对应信号的调制频率f0，表明能准确识别调制频率f0；在高频段，α=±2fc±f0及α=±4fc位置存在明显谱峰，表明能准确识别载波频率fc和调制频率f0。

根据 (8) 式计算循环平稳相关熵轮廓，结果如图13所示，图中的α=±f0，α=±2fc±f0及α=±4fc位置存在明显的谱峰。由于相关熵能有效抑制高斯噪声和脉冲噪声，因此循环平稳相关熵谱具有很强的从强高斯噪声和非高斯噪声中提取信号特征的能力，基于高斯核函数的循环平稳相关熵为高斯、非高斯噪声的处理提供了一种崭新的有效处理方法。

图13 循环平稳相关熵谱轮廓图Fig.13 Profile map of cyclostationary correntropy spectrum

为凸显循环平稳相关熵的降噪能力，将循环平稳相关熵谱密度与传统基于二阶统计量的谱相关密度进行对比，仿真调幅信号的谱相关密度即轮廓图如图14所示[23-24]，可以看出信号的能量分散在整个双频平面内，谱相关密度的能量聚集性很差，调制频率和载波频率完全被噪声掩盖，难以有效识别。

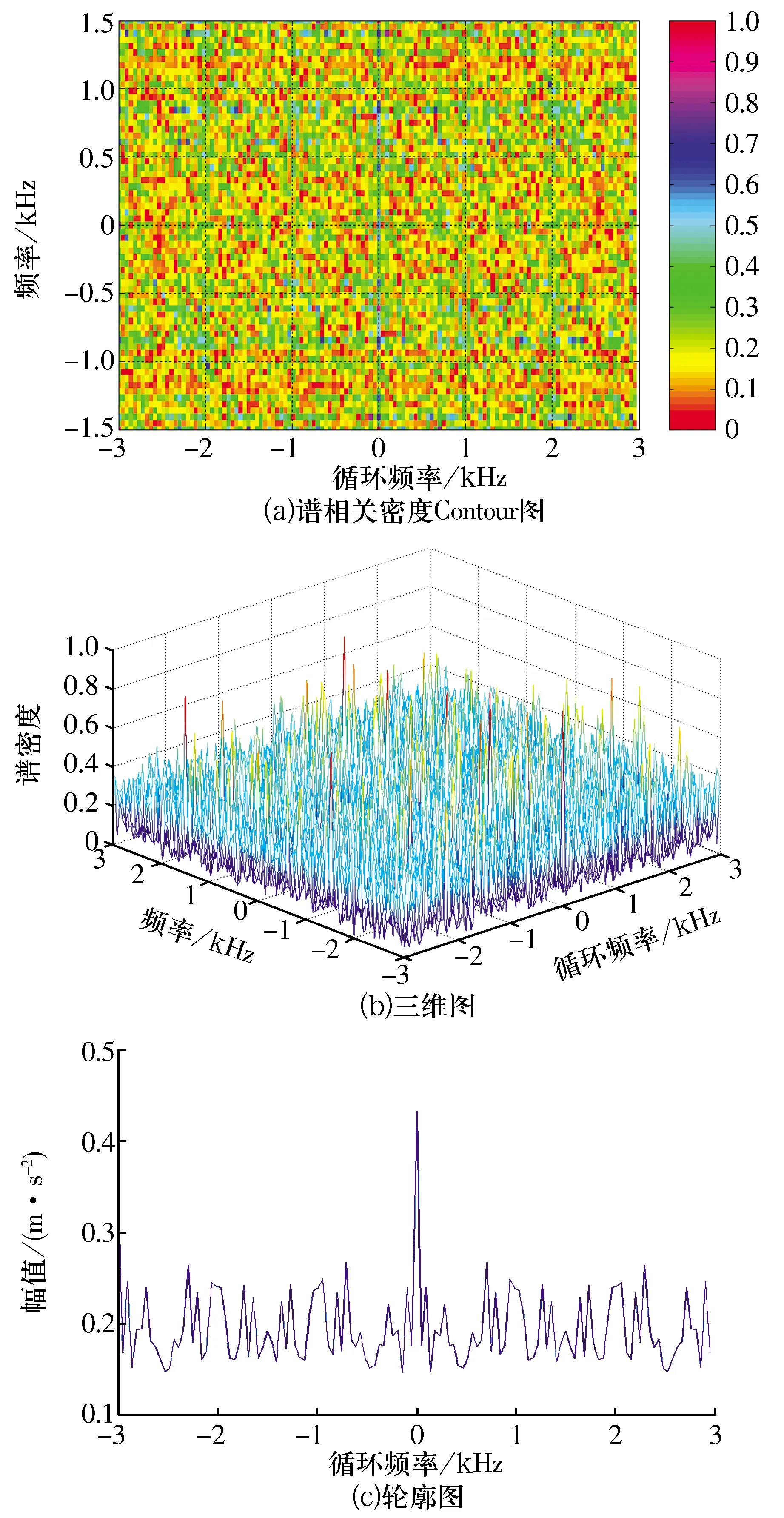
图14 仿真调幅信号的谱相关密度处理结果Fig.14 Spectral correlation density processing results of simulative amplitude modulation signal

4 实例验证

采用某型号齿轮箱输入端轴承进行试验，电动机额定转速为1 500 r/min，转频fr为25 Hz，采样频率为32 768 Hz。轴承型号为6208，球组节圆直径为97.5 mm，钢球直径为18.33 mm，球数为10。利用线切割机床分别在轴承内、外圈沟道上加工宽0.8 mm、深1 mm的局部裂纹，以模拟轴承内圈、外圈局部裂纹故障。计算[25]可得轴承内、外圈故障特征频率fi，fe分别为148.5，101.5 Hz。

4.1 轴承内圈故障

轴承内圈局部裂纹故障振动信号如图15所示，图中存在明显的幅值调制现象，但根据时域波形及其傅里叶变换无法有效识别轴承故障。

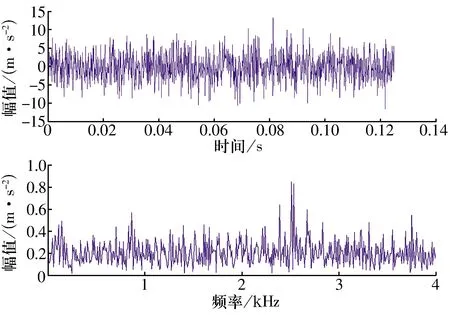
图15 轴承内圈故障振动信号及其傅里叶变换Fig.15 Vibration signal and its FFT with bearing inner ring fault

轴承内圈故障振动信号的循环平稳相关熵谱密度图如图16所示，由图可知：轴承内圈故障频谱特征是由循环频率α与谱频率f构成的双频平面，轴承内圈故障特征频率fi及其倍频主要沿直线f=-0.5α分布，逐渐由频谱中心向外扩展成整个频谱平面。

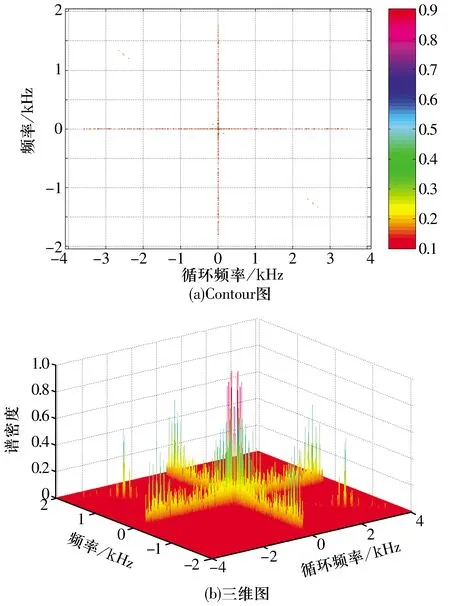
图16 轴承内圈故障振动信号循环平稳相关熵谱Fig.16 Cyclostationary correntropy spectrum of vibration signal with bearing inner ring fault

根据(8)式计算可得轴承内圈故障振动信号的循环平稳相关熵谱轮廓，如图17所示，由图可知：在循环频率α=±fr位置存在显著的谱峰，对应故障轴承所在轴的调制频率；在α=±fi±fr，α=±2fi±fr等轴承内圈故障特征频率及其倍频位置也存在明显的谱峰，清晰地刻画了轴承内圈故障信号的频谱特征。

图17 轴承内圈故障循环平稳相关熵谱轮廓图Fig.17 Profile map of cyclostationary correntropy spectrum with bearing inner ring fault

4.2 轴承外圈故障

滚动轴承外圈局部裂纹故障振动信号如图18所示，其循环平稳相关熵谱密度图如图19所示。由图可知：在循环频率α=±fe,α=±2fe等轴承外圈故障特征频率及其倍频位置存在明显的谱峰，这种频谱结构清晰表达了轴承外圈故障特征频率的分布特征。

图18 轴承外圈故障振动信号及其傅里叶变换Fig.18 Vibration signal and its FFT with bearing outer ring fault

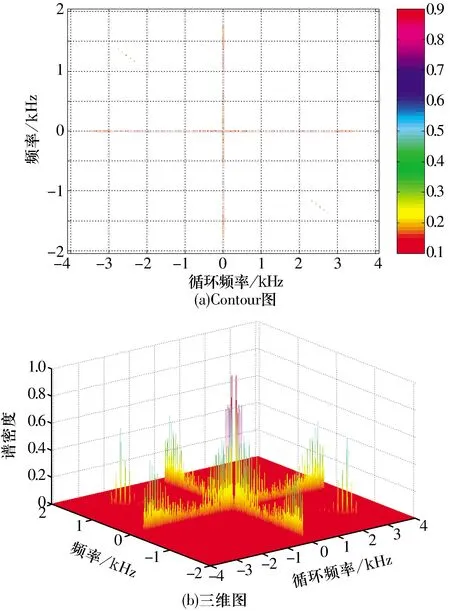
图19 轴承外圈故障循环平稳相关熵谱Fig.19 Cyclostationary correntropy spectrum of vibration signal with bearing outer ring fault

根据(8)式计算轴承外圈故障振动信号的循环平稳相关熵谱轮廓，结果如图20所示，由图可知,在轴承外圈故障特征频率fe及其倍频位置存在明显的谱峰，清晰反映了轴承外圈故障信号的频谱特征。

图20 轴承外圈故障循环平稳相关熵谱轮廓图Fig.20 Profile map of cyclostationary correntropy spectrum with bearing outer ring fault

4.3 小结

通过上述分析可以看出：循环平稳相关熵具有信号自解调功能，在由谱频率和循环频率组成的双频平面内，循环平稳相关熵谱密度能够清晰地刻画轴承内、外圈故障信号的频谱特征，具有从强染噪信号中提取轴承内、外圈故障特征的能力，提高了滚动轴承故障模式识别和特征提取的准确性和可靠性。

5 结束语

以理论分析和几何图解等方式系统分析了相关熵的降噪机理，用余弦信号和仿真调幅信号详细诠释了相关熵的降噪机理并验证了其抑制高斯噪声和随机脉冲噪声的能力。基于相关熵提出了循环平稳相关熵谱的轴承故障诊断方法,将循环平稳相关熵谱方法应用于轴承内、外圈局部裂纹故障诊断，试验结果表明循环平稳相关熵谱密度具有解调功能，能有效提取淹没在强噪声环境中的微弱信号，是一种有效的轴承故障诊断方法。下一步的研究可将循环平稳相关熵应用于风机、内燃机等复杂设备的故障诊断，也可将其作为一种信号预处理手段，与深度学习方法相结合，自动完成故障特征提取和故障模式识别。