不对称双体船非线性横摇阻尼及横摇运动分析

张艺瀚 王平 胡景丰

(中国船舶及海洋工程设计研究院，上海 200011)

根据目前研究成果，不对称双体船可以分为两类。一类是主体与片体大小及形状相同的船型，类似于常规双体船，但每个片体均按照中纵剖面不对称的线型设计；对于这种船型，目前的研究较多，主要集中在阻力、水动力干扰及线型优化方面，也有少数关于耐波性的研究[1- 3]。作为文中的研究对象，另外一类不对称双体船的两个片体尺度和排水量均不同，但单个片体关于中纵剖面是对称的，“亚洲女士号”游艇就是一个实船例子；目前对于这类不对称双体船的研究较少，很多耐波性能及特点没有被发掘。与单体或双体船相比，这类不对称双体船通过不对称双体的纵向错位和横向间距的移动来改变横摇、纵摇、升沉等耐波性能。Yu等[4]应用模型试验方法研究了错位不对称双体船的阻力和水动力干扰问题。Kim等[5]基于计算流体动力学(CFD)方法，通过尾部轴隧形状的优化设计改善了不对称双体船型的纵倾。

横摇运动一直是多体船水动力研究的重点，也是船舶六自由度运动计算中最为复杂的一个方面，其中横摇阻尼的确定是关键因素。不对称双体船横摇阻尼的求解相比于常规船需要考虑更多复杂的因素，主要是不对称性造成的流体干扰强非线性效应。目前，借鉴常规对称多体船，横摇阻尼预报主要通过船模试验方法确定，也可以通过数值计算和经验公式确定[6]。Zhang等[7]研究了三体船非线性横摇阻尼的处理方法，通过试验和理论两种方法计算了非线性横摇阻尼，并对横摇阻尼的非线性成分作了系统的分析[8]，提出了计算三体船摩擦阻尼和漩涡阻尼的经验公式，但无法考虑不对称双体船侧体之间的干扰引起的非线性效应。CFD数值水池考虑了流体粘性，已被广泛应用于多体船的横摇阻尼研究中。Simone和Metin等[9- 10]针对DTMB5415船型分别应用动网格和重叠网格技术进行了横摇衰减模拟，朱仁传等[11]应用相同方法进行了单体船横摇运动的数值模拟，笔者前期应用滑移网格方法对三体船型的非线性横摇阻尼进行了CFD模拟[12]。

目前，针对不对称双体船横摇阻尼和横摇运动的数值模拟求解尚未见深入的研究，文中采用理论与试验相结合的方法，对非线性横摇阻尼及波浪中横摇运动方程的数值求解进行研究，分析不同横向间距和纵向间距对横摇阻尼和横摇运动的影响，揭示不对称双体船横摇运动的性能及特点，以期为这类船舶的设计优化提供参考。

1 非线性横摇阻尼

1.1 CFD计算模型

1.1.1 计算原理及模型

船舶非线性横摇时，流体往往处于湍流状态，运动极不规则，速度等流动特性随机变化，漩涡不断形成和消失，表现出强非线性特性。对于湍流，由于其计算量较大，直接求解瞬时方程十分困难，通常采用时间平均法进行Navier-Stokes(N-S)方程的简化求解[8]，也就是先求解RANSE方程，同时应用湍流模型使N-S方程封闭，进而求解。标准k-ε模型针对充分发展的湍流建立，适用于高雷诺数的情况。k-ω模型也是常用的湍流模型，Begovic等[13]比较过用k-ε与k-ω模型求解的单体船横摇衰减运动，发现两者误差在1%以内，很难观察到差异。Starccm+平台的sstk-ω模型经常被用于横摇衰减运动的数值计算[9- 10]，文中采用sstk-ω湍流模型来研究不对称双体船的横摇衰减运动。

研究中以2 500 t不对称双体救援船为对象，其主尺度参数如下：主体的垂线间长Lpp,主体=100 m，型宽B主体=10 m，吃水T主体=4.2 m，排水量Δ主体=2 300 t；侧体的垂线间长Lpp,侧体=50 m，型宽B侧体=2.5 m，吃水T侧体=2.6 m，排水量Δ侧体=200 t，纵向间距SL=0～26 m(4组)，横向间距CL=8～22 m(8组)。为了研究不同纵向间距和横向间距的性能，分别在纵向间距和横向间距不固定的情形下展开研究。图1为不对称双体船的三维模型和横剖面型线，计算模型缩尺比为1:35。

1.1.2 计算收敛性分析

图1 不对称双体船的三维模型和横剖面型线

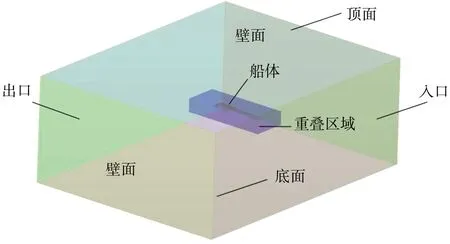
图2 重叠网格计算域示意图

(a)粗网格

(b)中等网格

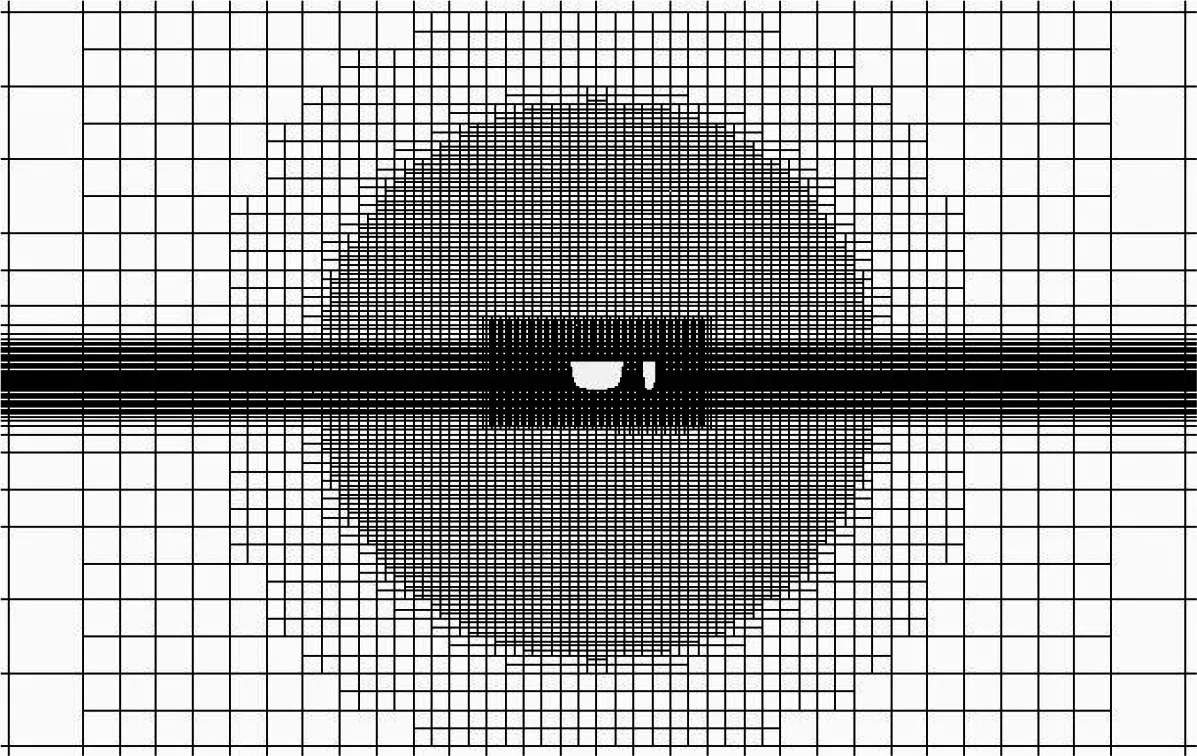
(c)细网格

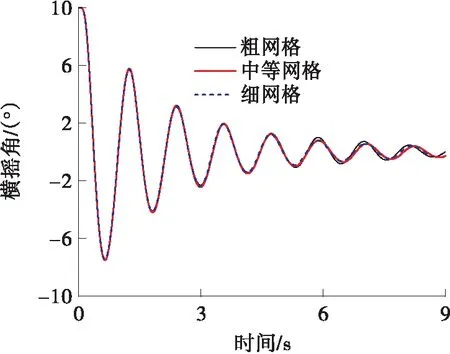
图4 不同网格精度下的横摇衰减曲线

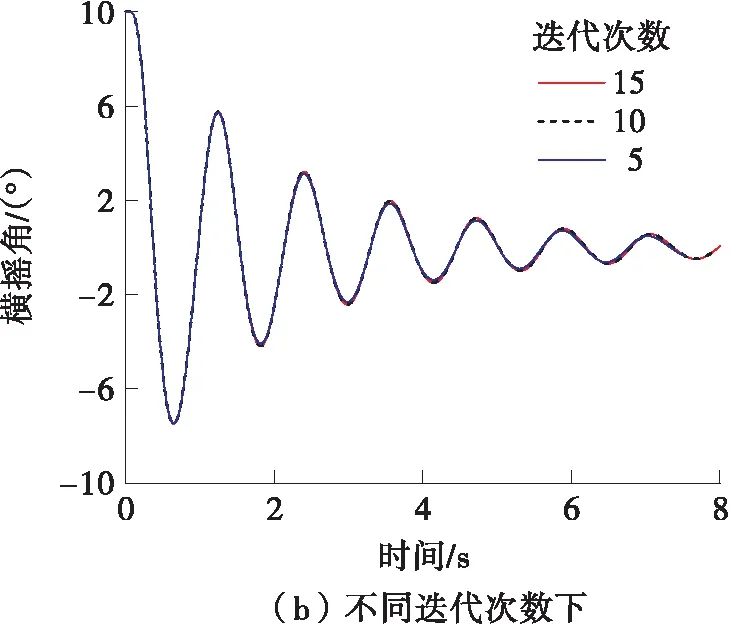
图5 两种情况下的横摇衰减曲线

收敛度Rk可以定义为

(1)

根据Rk的大小，不确定度有3种情况：①单调收敛，01。

针对单调收敛，通用的Richardson推断法(RE)可用于评估不确定度Uk和误差δRE，

(2)

式中：rk为统一的优化指数；Pk为精度阶数，

(3)

不确定度可根据安全因子方法确定：

(4)

Fs为安全因子，可参考ITTC[15]推荐取Fs=1.25。

由于迭代次数对横摇衰减曲线的影响较小，故文中针对网格尺寸和时间步选取衰减曲线首、中、尾3个峰值(时间t分别在1.25、4.75、8.20 s附近)进行不确定度的计算，计算结果如表1所示。由表中可知，各时间点下网格尺寸和时间步的不确定度都很小，采用中等网格和0.005 s的时间步可以达到足够的精度要求，使计算结果收敛。

表1 3个峰值的不确定度分析结果

1.1.3 模型试验验证

为了进一步验证CFD模拟对于不对称双体船型的适用性，开展了船模横摇衰减试验。试验采用CL=10 m、SL=0 m的模型，模型缩尺比保持和CFD数值计算一致(λ=1:35)。图6为CFD模型试验与数值计算的横摇衰减曲线对比，可见两者吻合较好。

图6 CFD数值计算与模型试验的横摇衰减曲线对比

1.2 横摇阻尼分析

1.2.1 横摇阻尼计算方法

非线性横摇阻尼通常为线性加平方的形式和线性加立方的形式，根据Zhang[8]对三体船的研究成果，多体船型的非线性横摇阻尼可采用线性加平方的形式，平方阻尼关系和平方衰减关系分别如下：

(5)

(6)

式中，a和b为衰减系数，A和B分别为线性阻尼系数和非线性阻尼系数，φ为横摇角，φm和Δφ分别为横摇衰减曲线相邻两幅值的平均值和相邻两幅值之差。根据衰减系数，可通过式(7)计算横摇线性阻尼系数A和非线性阻尼系数B：

(7)

式中，m为全船质量,GM为初稳心高，ω0为横摇固有圆频率。横摇阻尼系数经无因次化可表示为

(8)

其中，2μ、μ2分别为无因次线性阻尼系数和无因次非线性阻尼系数。

1.2.2 不同间距下的横摇衰减分析

应用上述方法计算了8组横向间距(实船CL分别为8、9、10、11、12、14、18和22 m)的静水横摇衰减曲线，结果如图7所示。可以发现，相比常规单体船[9]，不对称双体船的横摇衰减速度很快，只需要6～8个周期就可以衰减到较小的角度。总体上，随着横向间距的增加，衰减速度变快，衰减幅度增大，这个趋势在间距较小的几组变化中较为明显，横向间距增加到一定程度后，当CL≥12 m时，如图7(b)所示，前几个周期的衰减幅度相差不大，但后几个周期的横摇角衰减无规律。通过分析波高图和横切波面图(见图8)可以发现，不对称双体船的侧体在发生横摇时会产生兴波，对于横向间距较小如CL=8 m的情形，兴波较小且能很快在两者之间消散。随着横向间距的增大，兴波较大，如CL=22 m时，兴波到达主体后会造成船体的扰动，横摇角有突然增大的现象，这种现象是由不对称双体船的特殊船型引起的。

图7 不同横向间距下的横摇衰减曲线

图9为不同纵向间距下的实船横摇衰减曲线。可以看出，随着纵向间距的变化，横摇衰减曲线基本上保持一致，可以认为纵向间距对不对称双体船在零速时的横摇阻尼没有影响，故文中不再对不同纵向间距下的阻尼系数作进一步比较。

表2为不同横向间距下的实船横摇阻尼系数计算值。从表中可知，随着横向间距的增大，横摇阻尼系数整体上呈上升趋势，线性阻尼系数不断增加，而非线性阻尼系数先增加后减小，当CL≥12 m 后，非线性效应几乎消失。从物理上解释，是因为间距从0开始增大后，主体和侧体之间的水动力干扰逐渐增强，但增大到一定距离后这种干扰逐渐减弱。

CL=8 m

CL=12 m

CL=22 m

CL=8 m

CL=12 m

CL=22 m

图9 不同纵向间距下的横摇衰减曲线

表2 不同横向间距下的实船横摇阻尼系数计算值

1.2.3 不同航速的影响

图10为不同航速下的实船横摇衰减曲线，从图中可以发现，航速效应会使横摇衰减加快，有航速时的横摇阻尼将明显大于零航速时的横摇阻尼，这与单体船和三体船的研究结论类似[9,12]。但是，由于不对称船的特点，有航速时将造成不对称横倾力矩，使平衡角不再是正浮状态，且航速越快偏移角越大，这也是不对称双体船的一个特性。

图10 不同航速下的实船横摇衰减曲线

2 波浪中双体船的非线性横摇运动分析

2.1 基于势流理论的非线性横摇阻尼修正

虽然利用单自由度非线性横摇运动方程可以直接通过数值计算求解非对称双体船在波浪中的横摇运动，但无法考虑纵摇垂荡等耦合作用的影响。有鉴于此，文中基于三维势流理论建立如下六自由度运动方程组：

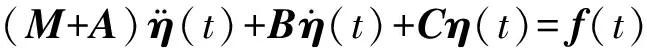
(9)

式中，M、A、B、C、η(t)、f(t)分别为质量矩阵、附加质量矩阵、阻尼矩阵、恢复力矩阵、六自由度运动列向量和波浪力。

考虑非线性横摇阻尼后，为了求解方便，根据等效线性化原理得到线性化横摇阻尼如下[12]：

(10)

式中，φa、ω分别为横摇幅值、波浪圆频率。线性和非线性阻尼系数A、B通过CFD计算得到。

不对称双体船大幅横摇时由于片体出水等影响,会造成恢复力的非线性，本文采用如下非线性恢复力模型：

C44=r1φ+r3φ3+r5φ5

(11)

式中，C44、r1、r3、r5分别为横摇恢复力系数、线性恢复力系数、3次方恢复力系数和5次方恢复力系数，可根据静水恢复力曲线拟合得到[16]。

根据上述基于势流理论的非线性横摇阻尼修正方法，可计算不对称双体船在规则波中的横摇运动响应，水动力计算模型如图11所示。

图11 水动力计算模型

2.2 横摇运动的数值计算结果分析和模型试验验证

计算航速为0、18和25 kn，由于本船为几何非对称形式，左舷横浪和右舷横浪将出现不同的响应结果，因此浪向角取0°～360°的全浪向范围。同时，文中还开展了CL=10 m、SL=0 m的船模在不同航速下的横摇运动响应试验，模型缩尺比为1:35，如图12所示。试验在哈尔滨工程大学拖曳水池中进行，水池的主尺度为108.0 m×7.0 m×3.5 m。

图12 船模试验照片

船模通过多功能适航仪连接拖车，横摇运动通过倾角传感器测量，部分横摇试验时历曲线见图13。可以看出，低频零点附近有程度较小的漂移现象，但这对结果的影响有限。实船横摇运动幅频响应的数值计算结果与模型试验结果的对比见图14，可以发现两者吻合较好。由于船体的左舷和右舷呈非对称构型，因此浪向角90°侧体横浪和270°主体横浪下的响应不同，侧体横浪下的横摇响应较主体大，因为这种状态下的主侧体流体兴波扰动更大。

图13 横摇试验的时历曲线

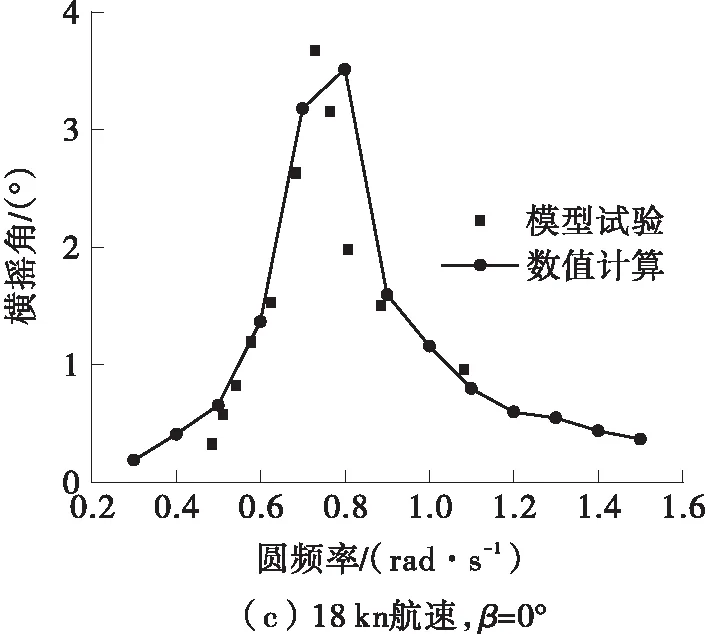
图14 横摇运动模型试验结果及数值计算结果对比

对于有航速的状态，横摇响应要小于零航速的值，这与常规多体船型及单体船型具有相似的规律。而25 kn航速时的横摇响应并不比18 kn航速时的小，这可能是因为航速效应导致了力矩不平衡。从横摇衰减曲线中也可以发现，25 kn航速时的横摇衰减相对较慢。

3 结语

文中采用基于重叠网格的CFD方法研究不对称双体船型的横摇衰减运动，并基于线性三维势流理论对非线性横摇阻尼和非线性恢复力进行了修正，得到了该船型在规则波中的横摇运动响应，结果表明，基于非线性修正的势流理论计算得到的横摇运动结果与模型试验结果较为吻合。

不对称双体船独特的构型特点使其横摇阻尼、横摇运动与常规单体船、对称双体船有很大的不同。因兴波干扰的存在，横摇阻尼随横向间距变化明显，而且线性阻尼和非线性阻尼有不同的变化规律。侧体上的横向波浪扰动相比于主体会造成更大的横摇响应。有航速情况下，不对称的构型还会产生横倾力矩，这对船舶的适航性造成一定的影响，需要在设计时利用必要的装置进行矫正。文中研究结果对于不对称双体船的设计具有一定的指导意义。