三面角内面角的大小及变化规律的研究

浙江省宁波效实中学(315012)童益民

立体几何中三面角内面角的大小及变化规律在动态中是一个比较难理解的问题,在高考与模拟考中也经常出现,学生对此类问题往往有错误的认识,总认为二面角的平面角大于相对的面角,并认为面角是单向变化的,解题上也是往往束手无策,本文试图通过三面角余弦定理与函数的思想解决这一系列问题.

三面角余弦定理如图1,由射线PA,PB,PC构成的三面角P−ABC中,∠APC=α,∠BPC=β,∠APB=γ,二面角A−PC−B的大小为θ,则cosγ=cosαcosβ+sinαsinβcosθ.(证明可见参考文献[1])

图1

问题一.当θ 变化时,研究γ 与θ 的大小关系

题目1如图2,已知ΔABC,D是AB的中点,沿直线CD将ΔACD翻折成ΔA1CD,所成二面角A1−CD−B的平面角为θ,则( )(选自2015年浙江高考理科第8 题)

图2

A.∠A1DB≤θB.∠A1DB≥θ

C.∠A1CB≤θD.∠A1CB≥θ

解法2(不通过结论1)如图3,作AO⊥CD于O点,延长交BC于E点,连接A1O,A1A.因为OE⊥CD,所以∠A1OE是二面角A1−CD−B的平面角,即∠A1OE=θ.因为A1D=AD≥A1O=AO,所以∠A1DA≤ ∠A1OA,所以∠A1DB≥ ∠A1OE,即∠A1DB≥θ,所以答案B 是正确的.而∠A1CB与θ的大小关系是不确定的,当θ=0 时,∠A1CB≥θ;当θ=π时,∠A1CB <θ.

图3

小结从题目1 的解法2 中,我们可以发现,不通过结论1 也可以很好的把题目解决,但需要特殊情况来排除,对面角与相对二面角的大小关系的整体情况,还是没有深刻的体会,但通过三面角余弦定理,可以对该类问题有清楚深刻的理解.知道了面角γ与相对的二面角的平面角θ的大小关系,接下来更难的是要弄清楚当二面角的大小θ固定,而α,β变化时,面角γ的变化规律是怎样的?

问题二.当α,β 变化时,研究γ 的变化规律

如图4,由射线PA,PB,PC构成的三面角P−ABC中,∠APC=α,∠BPC=β,α,β∈∠APB=γ,二面角A−PC−B的大小为θ,若AC⊥PC,BC⊥PC,则∠ACB=θ,当α,β变化,即PC的长度变化时,研究γ的变化规律.

图4

因为当PC的长度变化时,α与β是关联的,但它们之间的关系很难表示出来,所以用三面角余弦定理cosγ=cosαcosβ+ sinαsinβcosθ,很难用角α或β来研究角γ,所以引入新的变量PC.

图5

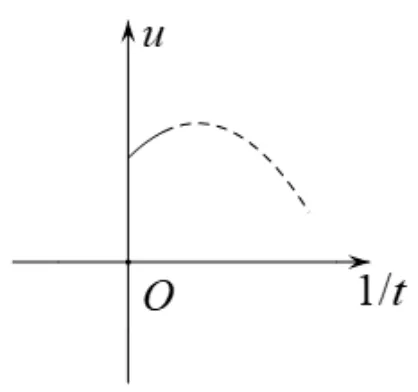
图6

图7

图8

图9

解析 ①是正确的,在此不作分析.②是错误的,因为假设AC=AD,BC=BD时,取CD中点M,则二面角A−CD−B的平面角为∠AMB,如图10.根据结论2,当∠AMB比较小时,P点从M点到C点,∠APB可先变大再变小,即可以∠AMB≤θ <∠ACB,同样也可以∠AMB≤θ <∠ADB,所以可以θmin=∠AMB,而不一定是θmin=min{∠ACB,∠ADB},这样②是错误的,答案为A.

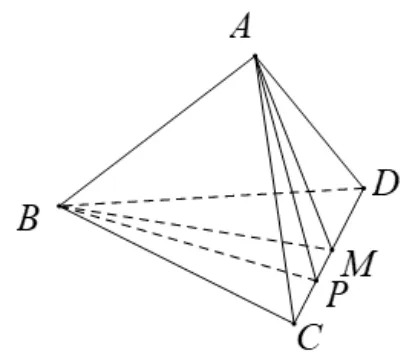
图10

总结题目2 中要得到∠APB的最小值是一个比较复杂的问题,首先要清楚的知道∠APB的变化规律,不要错误的认为P点从C点到D点,∠APB是单向变化的,或者错误的认为P点从M点到C(或D)点,∠APB是逐渐变小的.根据结论2,∠APB的变化规律不一定是单向的,根据不同的条件会有不同的变化规律,如果没有对问题二有非常清楚的认识,恐怕很难理解这道题目.