陀螺经纬仪在无定向导线测量中的应用研究
边 涛
(甘肃省地质矿产勘查开发局第三地质矿产勘查院,甘肃 兰州 730050)
由于矿山环境的复杂性,矿山测量就没有地表测量的便捷度,导致了测量人员在进行井下作业时无法按照设计的要求进行测量,井下光线暗淡、空间狭小,基本上测量方法都是以支导线的形式施测进行,方法单一,精度主要与测量人员的技术水平有很大关系,很难保障。按照现行规范要求支导线的施测不能超过一定的测站数和要求的距离,否则很难保证测量的精度,也达不到设计的要求,更有甚者影响后期的地质、采矿工作的准确性,尤其是在井下进行长距离双向贯通时。本章通过采用无定向导线加测陀螺经纬仪加强边来进行修正,通过无定向导线的布设,在长距离巷道中两边进行双向掘进时,在误差最大的控制点位和贯通点位100m 处进行陀螺加强边的测定,从而消除了转站引起的累计误差,提高了控制点位的测量精度,为后续的精准贯通提供了技术支撑。
1 无定向导线
无定向附和导线测量的原理就是导线点互相不能通视,没有起算方位角,导致观测的坐标不能计算。但在进行施测时可以按照支导线形式的施测方法进行观测,在进行点位坐标计算时不能采用支导线计算方法。
因此,在求解无定向附和导线的点位坐标时,常常假定一个方位角,从原有已知控制点上按照观测各个点位的角度、距离,利用坐标正算的方法计算各控制点位假定坐标,再附和到另一个已知的控制点上,根据各假定点位坐标和已知的控制点位坐标经过反算确定点位误差,改正分解距离误差、角度误差,从而确定真起始方位角,求得最或然真值。再经过坐标正算分个计算出各个假定点的真实坐标。通过精度估算及平差后确定无定向附和导线的各个点位坐标。本研究利用在井下进行无定向导线的布设,通过坐标计算反演,测量精度的改正,加测陀螺加强边,最终进一步的提高贯通精度。
2 陀螺经纬仪加强边的测量
陀螺经纬仪主要利用它的两个特性进行观测,是一种物理测量模式,利用它的进动性及定轴性从而测定真北方位角。每次测量结果都是独立的,测量误差不传递,也不会因为人的观测、计算产生累计误差。很好的保障了精度。近些年来,因矿山建设及生产越来越规范,测量技术水平的进一步发展,陀螺经纬仪得到了很广泛的应用,尤其在隧道贯通、竖井定向、巷道贯通等方面。所谓定向就是确定一条待定边的方位角,定向及方位角是测量中经常用到的,也是进行推导验算坐标时必不可少的一项条件,本研究采用陀螺经纬仪进行竖井内巷道定向,点位不需要通视,测定任意一条定向边,在点位误差椭圆上最大的导线点上进行加测陀螺定向加强边从而提高导线的测量精度,如图1 所示。

图1 陀螺定向示意图
3 应用实例
文章以玛曲县大水金矿为例,设计从地面开拓SJ891、SJ1071 至井下500m 处,在井下3310 中段双向贯通。SJ891 井口设计坐标为X=9313m,Y=1821m,高程为3759.37m。SJ1071 井口设计坐标为X=9201m,Y=2647m,高程为3589.79m。设计从3310 中段进行贯通,3310 中段设计长度为1682m,包含5 个平曲线。根据设计要求,SJ1071 将与现有SJ891-3310 中段贯通。预计贯通点K 的坐标为X=9128.090m,Y=3183.209m,高程为3310m。按照现有测量技术规范的标准,结合矿山测量的精度要求,在进行巷道贯通时横向的限差为0.5m,纵向的限差为0.2m,高程方面的误差为0.7m。我们从SJ891 和SJ1071 各投放一根钢丝,利用地表控制测量成果进行起算,采样连接三角形及前方交会的办法传递A 点、B 点的点位坐标。(如图2 所示):

图2 两井定向示意图
地表平面控制测量采用GPS 测量方案进行布设,利用原有的已知控制网,为了考虑原始点位的测量精度,进行局部加密,保证图形强度最好。在SJ891 洞口附近布设3 个控制点,尽量图形的内角为45°~65°,同理在SJ1071 井口附近也布设一组,与国家控制点进行联测。
无定向导线按照设计进行布设,同时兼顾井下施工的需要及不易破坏的原则。因两井在3310中段的实际距离约2.8km,考虑到井下巷道较多,且导线长度较短,单一支导线在进行测量时,转点越多,距离越远,累计误差越大,误差椭圆也就予大,即使复测多次也很难保证有很好的精度。因此采用无定向导线的形式在误差椭圆最大点位位置加测陀螺定向边,在SJ891-3310 中段巷道内S5-S6 短边,SJ1071-3310 中段巷道内S12-S13 短边进行施测,从而使得已有的支导线变成无定向附和导线,从而提高无定向导线贯通点位的精度。笔者采用了索佳-GP2X 陀螺经纬仪进行观测,陀螺经纬仪单次测量陀螺方位角中误差为15s。通过选取测区范围内四组控制点进行仪器常数的测定,用跟踪逆转点法独立测量两次,采用平差计算,求得仪器常数,同时选取井下同精度的四组控制点也进行一次仪器常数的测定,井上、井下采用加权平均值计算最终仪器常数,结合陀螺方位角最终计算北方位角,进而解算井下巷道内各控制点的点位真值。
4 平差及精度
本文通过利用俩竖井外的GPS 控制点解算井筒A、B 投点的精确坐标,井下设计的各个控制点。
4.1 贯通点K 在水平x′轴方向的误差
SJ891 在3310 中段巷道内起始点位及陀螺经纬仪的自身定向误差会影响到贯通点K 在横向上的误差,通过加测陀螺经纬仪加强边S5-S6,S10-S9,独立测量两次,利用Excel 编写的计算程序,解算巷道内贯通点K 的各个参数。(见表1、表2)。根据平差理论及技术规范,已知起始点中误差m0,起始边方位角中误差ma0,陀螺经纬仪一次定向边方位角中误差maT引起贯通点K 在x′轴上的误差为:

表1 SJ891-3310 中段无定向导线坐标及误差参数 单位:m

表2 SJ891-3310 中段无定向导线坐标第二段陀螺边误差参数计算 单位:m

式中,y′01,y′02-两段无定向附和导线点位重心在假定坐标系中的横坐标(见表1)。y′1,y′k-已知的起始点位和贯通点k 的假定横坐标y′1=476,y′k=0。井下的无定向导线测量和陀螺经纬仪测量各独立观测两次,巷道贯通点K 在水平方向横向上的预计中误差为:

同理:mαT引起贯通点K 在y′轴上的误差为:
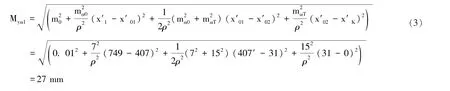
式中,x′01,x′02-两段无定向附和导线点位重心在假定坐标系中的横坐标。结果(见表1、2、3)。x′1,x′k-导线起点及贯通预计点的假定横坐标,x′1=-2666,x′k=0。
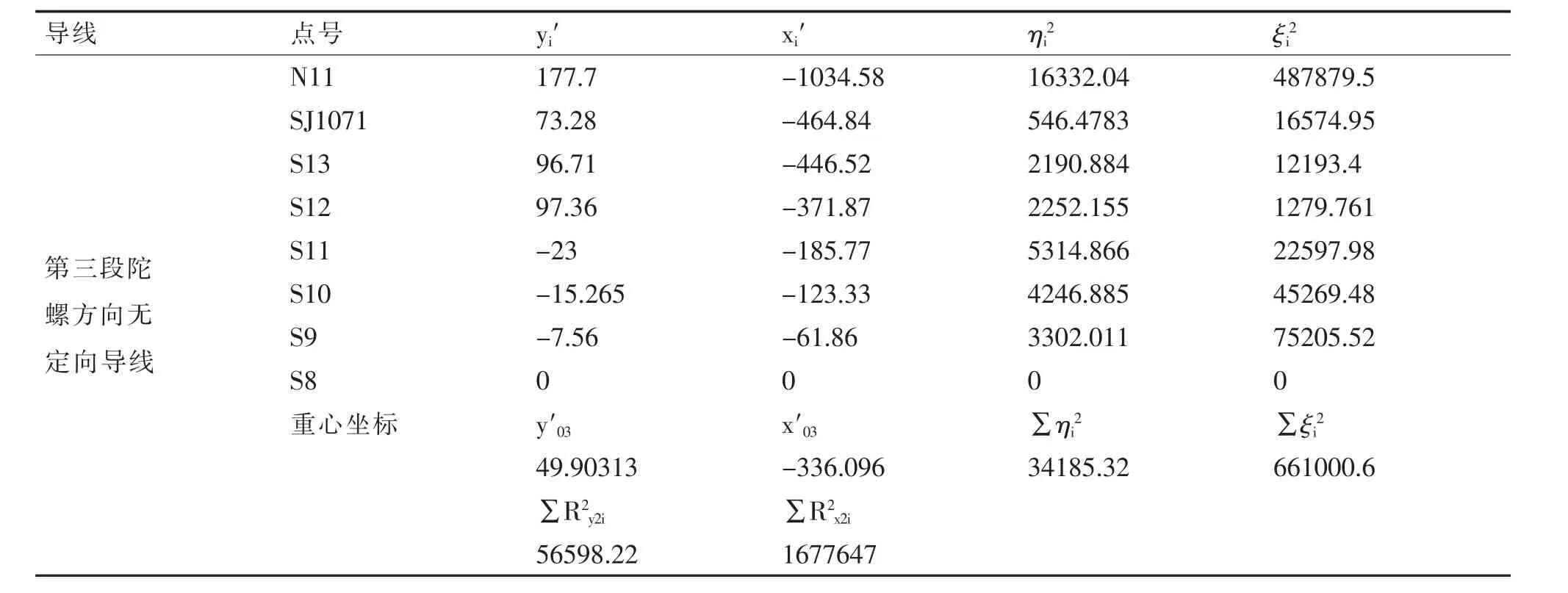
表3 SJ1071-3310 中段无定向导线坐标第三段陀螺边误差参数计算 单位:m
4.2 贯通点K 在水平y′轴方向上的误差
井下的无定向导线测量和陀螺经纬仪测量各独立观测两次,巷道贯通点K 在水平方向纵向上的预计中误差为:

4.3 贯通点K 在高程方向的总误差
井下无定向附和导线采用三角高程测量和水准测量的方法,独立进行两次测量,贯通点K 在高程方向的预计中误差为:

后期施工掘进时,在3310 中段贯通点800m 处进行两段陀螺经纬仪定向加强,计算贯通误差为Mxk=41mm,Myk=40mm,Mhk=48mm,进一步的修正了掘进方向,同时与无定向导线上的点位最或然值进行了比较,极大消除了累计误差,又降低了井下测量人员因观测造成的影响。同时为了进一步验证此方法,在3310 中段贯通点100m 处又进行了一陀螺经纬仪定向加强,计算贯通误差为Mxk=23mm,Myk=18mm,Mhk=25mm,相较于误差预计值进一步提高了精度,双向反演计算误差值在Mx=4mm,My=3mm,Mh=3mm,进一步验证了数据的可靠性,可见在无定向导线上加测陀螺经纬仪加强边能很好地提高贯通的精度。
5 结论
本文通过在无定向导线上加测陀螺定向边,既保证了测量数据的独立性,减少了累计误差,又很好地控制了测量精度,此方法不但对测量结果的精度提高了2 倍多,还解决了在互相不通视条件下如何快速提高测量精度,保障巷道在贯通时作业队伍的精准施工,从而降低不必要的返工和人、财、物方面的成本节约。

