考虑故障持续时间不确定的主动配电网随机优化调度
吴凯, 曹建伟, 陈家乾, 林捷, 胡成鹏, 张有兵
(1.湖州电力设计院有限公司,浙江 湖州 313000;2. 国网浙江省电力有限公司 湖州供电公司,浙江 湖州 313000;3. 浙江工业大学 信息工程学院,浙江 杭州 310023)
0 引 言
全球气候变暖导致台风和地震等极端自然灾害频发,随之产生的大规模停电事故给电网造成了重大的经济损失[1]。然而,多种类型的分布式电源接入主动配电网使得系统在严重故障后自主支撑本地重要负荷成为可能。因此有必要研究在主动配电网遭遇极端灾害时分布式电源的调度方案,以减小停电损失,提高配电系统供电可靠性。
分布式电源包括可再生能源、小型燃油/汽轮组以及储能系统,其中可再生能源出力的随机特性给配电网稳定运行带来了严峻挑战。此外在极端灾害导致的故障事件中,系统故障的持续时间也是不确定的。为了应对上述多重随机性,需要设计有效的随机优化方法来规避随机因素带来的风险。
目前已有较多文献考虑配电网不确定性进行优化调度建模,文献[2]采用三阶段鲁棒优化模型,以在最坏运行场景下系统切负荷量最少为目标求解电动汽车最优配置,但是仅考虑最恶劣情况会导致优化方案较为保守。文献[3]考虑孤岛运行模式下主动配电系统恢复问题,但模型中未考虑风险管理,难以控制调度方案在小概率场景中的切负荷风险。
基于以上文献所存在问题,本文提出了一种两阶段能量管理方法,旨在保证系统经济效益的同时,最大化规避不确定因素带来的切负荷风险。针对故障的不确定性问题,利用概率分布模拟故障持续时间。同时,考虑到小概率事件带来的严重损失,在优化模型中,通过风险管理保证调度策略在小概率场景中的适用性。所提双层优化模型在上层模型进行功率优化,而下层模型进行最优潮流,通过设计交替迭代算法求解模型。案例分析验证了所提方法的有效性。
1 系统建模
1.1 不确定性建模
故障持续时间可以由概率分布来模拟,而概率分布一般需要通过历史数据拟合而成。根据文献[4]对电力系统停电时间分析研究,本文采用正态分布来模拟故障持续时间的不确定,并将通过抽样形成相应的场景集。具体步骤如下。
(1) 根据预测数据,采用蒙特卡洛抽样的方法,生成N个预测场景,其中每个预测场景中包括可再生能源出力和负荷需求的数据,每个场景的概率均为1/N。
(2) 采用后向削减法,将预测场景数量削减到合适的数量,同时计算出相应预测场景概率和可再生能源出力以及负荷需求。
(3) 考虑ψ种故障持续时间的可能性,用HN表示预测场景N发生的概率,Dψ表示故障持续ψ时间的概率。两种不确定问题组合成共S=N×ψ种运行场景[5],场景概率如图1所示。

图1 场景概率图
1.2 主动配电网上层优化模型
1.2.1 目标函数
在上层优化模型中,以运行成本最低为目标函数,同时考虑风险管理:
min(1-α)Fpower+αFCVaR
(1)
Fpower=(1-β)(FDG+FRES+FFU+FESS)+βFLOAD
(2)
式中:Fpower、FCVaR、α分别为运行成本,运行风险以及风险管理的权重值;FDG、FRES、FPU、FESS、FLOAD、β分别为燃油/汽轮组成本,可再生能源成本,系统与大电网交互功率成本,储能成本,切负荷成本和经济性指标与故障指标的权重值。
(1) 燃油/汽轮组成本表示如下:
(3)
式中:S、s、ps分别为总的运行场景个数,当前优化的运行场景以及该场景对应的概率;T、t分别为总优化时长和当前优化时段;Δt为优化间隔;Ps,d,t为燃油/汽轮组的输出功率;Cd为燃油/汽轮组的成本系数。
(2) 可再生能源运行成本,系统购售电成本和切负荷成本分别由式(4)~式(6)表示。
(4)
(5)
(6)
式中:Ps,w,t、Ps,p,t分别为风机和光伏的输出功率;Cr为可再生能源的成本系数;Ps,u,t、Cu分别为交互功率和实时电价;td为故障开始时间;LSs,t、VOLL分别为切负荷量和切负荷成本系数。
(3) 储能运行成本表示如下:
(7)
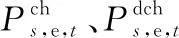
(4)在随机优化问题中,由于多种场景之间存在的差异性较大,使得优化方案在小概率场景中可能会产生非常高的运行风险。为了避免这种不利情况的出现,随机优化方法一般都采用风险管理模型。根据已有文献分析研究,本文采用条件风险价值(conditional value at risk,CVaR)来衡量风险水平[6],计算方法如下:
(8)
式中:η为置信度;θs,ψ、λ为用以计算CVaR而引入的辅助变量。
1.2.2 约束条件
(1) 燃油/汽轮组运行约束
(9)
Ps,d,t-Ps,d,t-1≤URd
(10)
Ps,d,t-1-Ps,d,t≤DRd
(11)
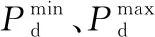
(2) 储能运行约束
(12)
(13)
(14)
(15)
(16)
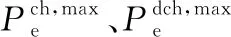
(3) 负荷运行约束
0≤LSs,t≤Ps,l,t
(17)
式中:Ps,l,t为负荷需求量。
(4) 功率约束
(18)
(19)
式中:Ps,loss,t为网损值。
(5) CVaR约束
Fs,power-λ≤θs,∀s
(20)
θs≥0,∀s
(21)
式中:Fs,power为s场景中功率运行成本值。
1.3 主动配电网下层优化模型
1.3.1 目标函数
在下层优化模型中,以网损最低为目标函数进行优化:
(22)
式中:Ωb为全部支路的集合;rij为支路ij的电阻;Is,t,ij为支路ij的电流;Closs为网损成本系数。
1.3.2 约束条件
(1) 潮流约束
(23)
(24)
(25)
(26)
式中:Ps,t,ij、Qs,t,ij分别为支路ij的有功、无功功率;Ps,t,i、Qs,t,i分别为节点i的注入有功、无功功率之和;xji为支路ji的电抗。
(2) 系统运行约束
(27)
式中:Umin、Umax分别为系统允许节点电压的上下界。
针对下层优化模型中的非线性项,采用二阶锥松弛[7]将其转变为凸优化模型,进而通过已有优化工具进行求解。
1.4 主动配电网两阶段优化算法
本文所求解目标是多场景下的期望值,意味着在求解过程中计算复杂度较大。为此,考虑通过将功率优化和潮流优化解耦计算,设计两阶段优化算法来求解模型,在保证求解准确性的基础上显著提升求解效率。主动配电网两阶段优化流程如图2所示。

图2 优化流程图
(1) 根据预测数据和所设方差生成大量预测场景并削减至一定数量。
(2) 将预测场景集与故障持续时间结合,生成模型所需运行场景集。
(3) 功率优化阶段,计算出各个场景中分布式电源在各时段中的最优调度功率。
(4) 潮流优化阶段,计算出在各个场景中的最优潮流分布,并保存各时段的网损值。至此,完成一次迭代计算。
(5) 计算出两次迭代中网损的差值,若差值达到收敛条件,则优化结束;若差值未达到收敛条件,则根据更新的网损值,继续进行下一次的迭代计算。
在第一次迭代计算时,功率平衡方程中的网损值应置为0,在此基础上计算出分布式电源的调度方案并代入下层模型中求解最优潮流,通过交替迭代,最终得到优化方案。
2 系统参数
本文在修改过的IEEE33节点配电系统中进行测试,分析验证本文所提方法的适用性和正确性。系统拓扑结构如图3所示。

图3 系统拓扑结构
不确定性变量预测数据的曲线如图4所示。在本文中,对负荷需求,风机以及光伏的方差分别设置为各自预测值的3%,10%以及5%。对于故障持续时间的不确定性,用平均值为5 h、标准差为1 h的正态分布来模拟,离散化后的概率分布如表1所示。

图4 各时段预测数据的曲线

表1 故障持续时间概率表
燃油/汽轮组参数如表2所示。储能的容量设置为1.6 MW·h,荷电状态设置为0.20~0.95,并假设储能在故障发生前电能已充满,充放电能设置为0~0.25 MW·h,充放电效率为0.88。α、β、η分别设为0.95、0.90、0.90,VOLL设为7 000 元/(MW·h),Closs设为560 元/(MW·h),Umax和Umin分别为1.05和0.95。

表2 分布式电源配置参数
3 算例分析
本文设计了三个案例来分析验证所提优化方法的有效性,并假设故障发生在8:00,故障导致线路L1-2断开,经故障隔离,下游区域与上级电网断开连接,导致故障下游的系统全部失电。
案例1:利用随机优化理论进行优化调度,但不考虑风险管理。
案例2:与案例1一致,只是仅考虑最恶劣情况,即故障持续时间为8 h。
案例3:与案例1一致,同时考虑风险管理。
3种案例下储能的调度策略如图5所示,案例2仅考虑最恶劣的故障情况,导致储能放电缓慢,使得调度策略过于保守。在考虑故障持续时间随机性的案例1和3中,由于故障持续时间超过6 h的概率较低,储能几乎完全放电至14:00。与案例1相比,案例3由于考虑了风险管理,因而不会在14:00和15:00对储能进行充电,降低了调度策略在小概率场景中的切负荷风险。

图5 各案例下的储能调度策略
3种案例优化结果如表3所示。可以看出,基于最恶劣情况的案例2过于保守,导致运行成本最高,说明在处理不确定性问题时,如果仅考虑最极端的情况,会极大降低优化结果的经济性。案例1与案例3相比,虽然案例3的运行成本比案例1大,但是CVaR有了明显改善,规避了小概率场景带来的高风险损失,由此可见,通过牺牲一定的运行成本来大幅度降低风险水平是有必要的。
对3种案例所产生的调度策略在不同故障持续时间下的切负荷成本进行测试,结果如图6所示。由于案例1没有计及小概率场景,在故障持续时间超过6 h的情况下,面临着严重的切负荷风险。案例2的切负荷成本只有在故障持续时间8 h的情况下才显示出较低水平。而考虑风险管理的案例3产生的切负荷成本在不同故障持续时间中均能保持较低水平,并且在最恶劣情况下的切负荷成本也可以与案例2保持一致。

表3 3种案例优化结果

图6 不同故障持续时间下切负荷成本图
4 结束语
本文提出了一种应对多重不确定性的两阶段主动配电网能量管理方法,通过双层优化模型最小化系统运行成本的期望值,并采用显著降低不确定因素带来的切负荷风险,使得调度策略在小概率场景中能保持良好的风险控制特征。在此基础上,通过二阶锥松弛将模型转化为凸优化模型,并设计两阶段迭代优化方法将模型解耦,显著提高求解效率。算例分析表明,在应对极端故障时,所提方法可以帮助系统在保证经济效益的同时,显著降低切负荷风险。

