线性图态的量子测量与量子门操作的等价性

唐彦立，朱佳莉，吴晓宇

(1.南京邮电大学理学院，江苏南京 210023 2.南京邮电大学通信与信息工程学院，江苏南京 210003)

在量子计算（Quantum Computing） 中，图态［1－8］（Graph State）是一种可以用图表示的量子纠缠态，可以直观地表示量子纠缠态。基于测量的量子计算（Measurement-based Quantum Computing，MBQC）是目前构建全光子量子计算机的最可行的方法，它通过测量图态中的量子比特（qubit）序列实现在图态的不同物理层之间传播信息来运行算法［9－11］。此外，图态在量子纠错码、纠缠测量和纯化中也有很多应用。

对图态的测量与门操作之间的等价性在文献［12］中也有提到，但文献［12］只给出了三维以及五维的线性图态的等价关系式，且所给对应关系有误。

为了寻找到正确的对应关系，本文将结合具体的计算推导，介绍探索的过程，即对线性图态中存在的规律进行归纳和延伸。

本文首先以2-qubit线性图态｜L2〉和3-qubit线性图态｜L3〉为例，从中找到对图态的量子比特的测量与量子门操作之间的对应关系。接着，通过推导以及表达式变形，将｜L2〉和｜L3〉的表达方式统一起来，发现了优美的等价规律。由此思考该对应关系是否可以适用于更高维度的线性图态。最后采用数学归纳法，证明了任意的n-qubit线性图态（n≥2）都满足该等价性关系。

1 基础概念

1.1 图态（Graph State）

图态（Graph State）是一种量子纠缠态，可以用图形直观地表示。在图态中，每个顶点代表一个qubit，每根连线表示一种关联。

不同的点线组合，可以构成不同的图态，较常见的有线性图态、星形图态、双分支图态等。其中，双分支图态在量子纠错和容错方面有广泛应用，例如，通过将一个逻辑qubit编码在双分支图态中的两个（物理）qubit上，从而减少相位翻转错误、提高容损性、提高抗噪性能等［12］。而星形图态也是一类具有典型代表性的图态，它以一个顶点为中心，其他顶点都与该点相连。从星型图态可以较容易地演变出其他各类图态［12］。

线性图态是最简单也是最基础的图态，在研究其他各类图态时，往往都离不开线性图态，因此对线性图态的研究显得尤为重要。本文即以线性图态为研究重点，探索其性质。为了对线性图态有一个具体的印象，读者可以先看第2节中的图1和图2，两者分别展示了线性图态｜L2〉和｜L3〉。

1.2 测量基的数学表示以及物理含义

首先介绍基矢｜0〉和｜1〉，从数学的角度可以将其表示为二维的矩阵

他们构成了一组正交完备归一基。而从物理的角度，这两个基矢有很多的含义，例如光子的偏振［13－15］，用｜0〉代表光子处于水平偏振的状态，那么｜1〉代表竖直偏振的光子态，这在量子密钥分发［16－22］（Quantum Key Distribution） 中有不少应用；此外，这两个基矢还可以表示粒子的自旋［23－25］等。

本文推导中还用到了对角基｛｜＋〉，｜－〉｝，它们是｜0〉和｜1〉的叠加态，表达式为

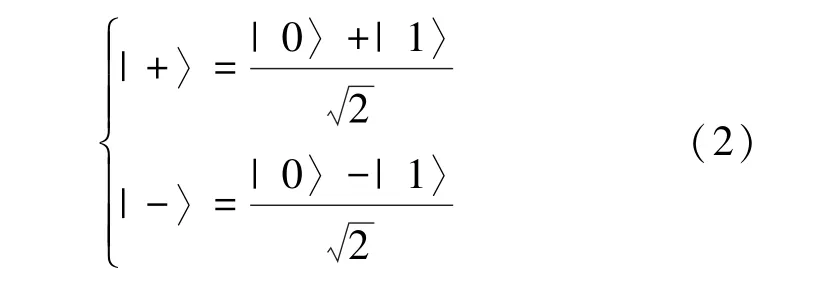
如果依然从光子偏振角度去理解对角基，以｜0〉为 x轴正向，｜1〉为 y 轴正向，那么对角基｜＋〉，｜－〉分别代表45°偏振和135°偏振的光子态。

本文中，选取以下测量基

其中的相位因子φ表示相对相位差，容易验证这是一组正交完备归一基。采用该测量基对图态的qubit进行测量。在探索过程中，通过将图态的表达式在该测量基下展开，继而寻找其中暗含的规律。

1.3 受控 Z 门（Controlled-Z gate）

本文主要用到二量子比特的受控Z门，用算符CZ表示Controlled-Z操作，其表达式可以写为CZ＝I－2｜11〉〈11｜。 这是一个二量子比特算符，其作用是，当两个qubit同时为1时，会发生相位翻转，即多出一个因子eiπ＝－1，而对另外3个基矢不产生作用，即

为了简洁，该表达式略去了CZ的下标。

为了方便表达，用CZij表示该Controlled-Z操作作用在量子比特i和j上。

在本文的推导中，会用到如下的运算技巧

接下来参考文献［26］介绍推导过程中需要用到的单量子比特操作H、RX、RZ。

1.4 哈达玛门 H（Hadamard gate）

在本文中，涉及到的Hadamard门操作［26］，其矩阵形式为

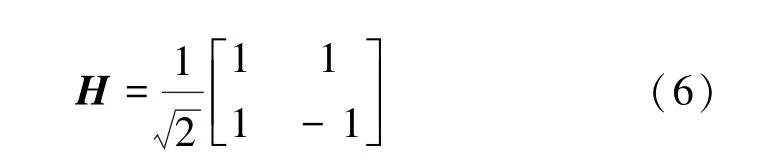
在推导过程中会用到如下的计算技巧

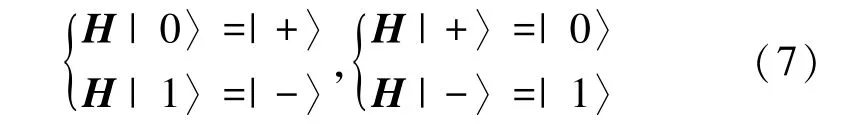
1.5 旋转算子（Rotation operator）

在引入旋转算符之前，先介绍一下Pauli矩阵X、Y、Z以及单位阵I

2 等价性的初步探索

首先，考虑最简单的例子｜L2〉、｜L3〉，将其表达式在测量基下展开并化简，寻找测量与门操作之间的等价规律。

在本节的推导过程中，主要用到H、RX、RZ的表达式（6）和（10）， H 的运算技巧式（7）和（9）， RX、RZ的转换关系式（11）和（12），以及CZ的运算技巧式（4）和（5）。

2.1 2-qubit线性图态｜L2〉

首先，考察｜L2〉的表达式，见图1。

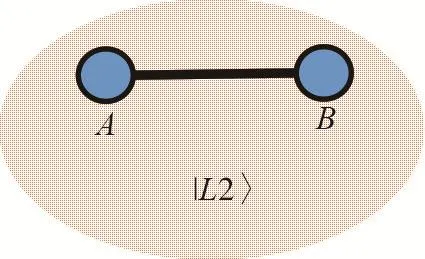
图1 二量子比特的线性态｜L2〉

图中的每个顶点代表一个量子比特（qubit），分别以英文字母A、B标识，两点之间的连线表明存在相互作用。

根据图态定义，A和 B首先制备为 ｜＋〉A和｜＋〉B，并将其视为一个整体，即将A和B看做一个系统，之间用直积符号“⊗”相乘，那么A和B构成的系统就表示成 “｜＋〉A⊗ ｜＋〉B”， 但为了表达方便，很多时候略去“⊗”，直接写为 ｜＋〉A｜＋〉B或｜＋＋〉AB。 然后，A与B之间的连线表示A、B之间进行一次CZ操作。由此，可以写出｜L2〉的表达式为

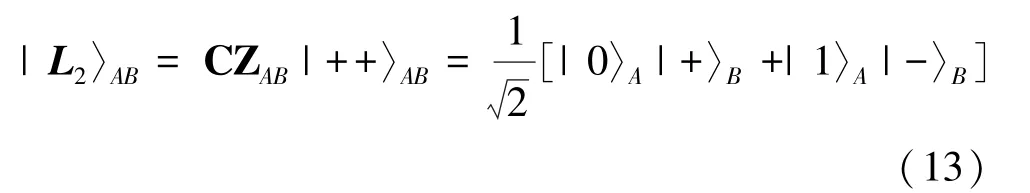
为了找寻测量与门操作之间的关系，对A进行测量，采用测量基 M（φ）＝｛｜0〉 ＋eiφ｜1〉，｜0〉 －eiφ｜1〉｝。 由式（3）可得关系式

由此可知，qubit A和B处于纠缠态。一旦用测量基 M（φ）＝｛｜0〉 ＋ eiφ｜1〉，｜0〉 － eiφ｜1〉｝ 去测量A，qubit A就会发生坍缩，且只有两种可能，要么是 坍 缩 到 ｜ψ（φ）〉A态， 要 么 是 坍 缩 到｜ψ⊥（φ）〉A态。

若qubit A坍缩到状态｜ψ（φ）〉A，那么qubit B就会坍缩到 e－iφ／2HR*Z（φ） ｜＋〉B， 由于共同相位因子 e－iφ／2不具有物理意义， 没有可观测效应［26］（Observable effects），所以将其忽略，并将qubit B简写为HR*Z（φ）｜＋〉B，可以看出，对 qubit A的测量，使得qubit B由 ｜＋〉B，先经历一次旋转门 R*Z（φ）操作，再经历一次哈达玛门H操作。可以发现，通过调整测量基M（φ）的角度φ，相应的作用在B上的门操作HR*Z（φ）也会随φ改变。在这里看到了对图态｜L2〉AB中qubit A的测量，等价于对qubit B进行了量子门操作。

同样地，若 A坍缩到 ｜ψ⊥（φ）〉A态，根据式（15），可以知道B 一定坍缩到了HR*Z（φ）｜－〉B，相当于让 B由 ｜－〉B经历同样的量子门操作HR*Z（φ）。

通过观察qubit A的测量结果是｜ψ（φ）〉A还是｜ψ⊥（φ）〉A，可以得知qubit B等价于经历了哪些量子门操作。

在寻找等价性的过程中发现，对2-qubit图态中的一个qubit的测量，等价于对另一个qubit作了量子门操作。

为了深入研究“对图态的测量”与“量子门操作”之间的等价性，接下来，将以｜L3〉ABC作为研究对象，来进一步分析等价性关系。然后将｜L3〉ABC与｜L2〉AB的结果进行比较，进而拓展到更高维的线性图态。

2.2 3-qubit线性图态｜L3〉

线性态｜L3〉见图 2。

图2 线性态｜L3〉

根据图态的定义，

对qubit A、B作测量，分别采用测量基 M（φ）和M（θ）。 为了考察qubit C会坍缩到什么态，将｜L3〉ABC中的 qubit A 在基底 ｛｜ψ（φ）〉， ｜ψ⊥（φ）〉｝下展开，同时将 qubit B 在基底 ｛｜ψ（θ）〉，｜ψ⊥（θ）〉｝ 下展开，并化简，可以得到

这是一个四项式，每一项代表着一种可能的结果，由于A在测量基M（φ）下有两种测量结果，B在测量基M（θ）下也有两种测量结果，组合之后2×2便是4种可能结果，表达式中的4项便对应着这4种可能的情况。可以看出，不同的测量结果相当于对C进行了不同的门操作。例如，若测得A、B的结果分别为 ｜ψ（φ）〉A、｜ψ（θ）〉B， 那么，C 的态相应地会坍缩到RX（－ θ）｜ψ*（φ）〉C；其他3种情况类似地去理解，可以看到，A和B的测量结果决定了C的测量结果，并且存在一定的规律。

可以发现，测量结果和门操作之间存在一一对应的关系，但这个规律，与2-qubit的情况不统一，难以推测出n-qubit线性图态的表达式。为此，继续对表达式进行变换，寻找更简洁的规律。

2.3 统一｜L2〉与｜L3〉的表达形式

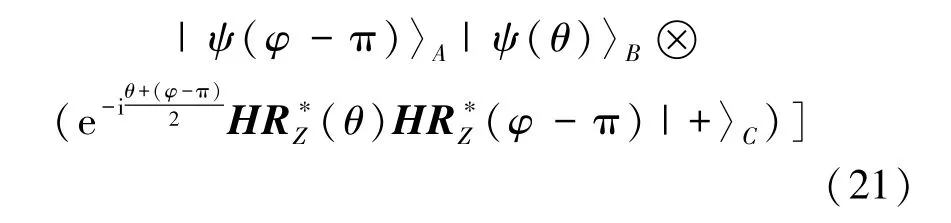
可以看到，式（21）体现了很规律的对应关系。它是一个四项式，每一项代表一种可能的测量结果，而这 4种可能的结果，可以统一表达，即，对｜L3〉ABC的A和B分别进行测量，若A坍缩到的态记为｜ψ（α）〉A，B坍缩到的态记为｜ψ（β）〉B，则C所坍缩到的态可以表示为｜＋〉C。

这样就概括了“α＝θ或θ－π，且β＝φ或φπ”这4种情况。

也就是说，根据A、B的测量结果｜ψ（α）〉A、｜ψ（β）〉B，得出α、β，那么，就可以判断出C态坍缩到了。 相当于将C由｜＋〉C进行了一系列门操作。

对于｜L2〉AB， 即式（20），可类似地去理解。

接下来，分别用图 3和图 4展示｜L2〉AB和｜L3〉ABC中“测量与门操作的等价性”。

图3 电路模型与等效的对｜L2〉AB的测量方案

如图3所示，上方蓝框内展示的是对qubitB进行量子门操作的电路模型，即对｜＋〉B依次进行量子门操作（α） 和H，得到｜ψout〉B＝（α）｜＋〉B。

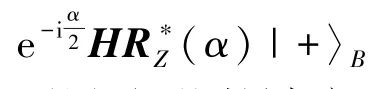
对比图3的这两个模型，可以看出两者之间是等价的，图中已用等价符号“”标识出。

此外，测量和门操作之间的等价性在图中用淡红色标识出，即

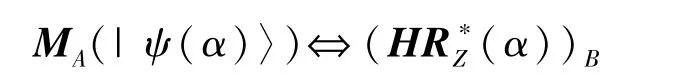
这便是本文所要寻找的等价性关系。其中，MA（｜ψ（α）〉）是对图态的测量（下标A表示测量对象为 qubitA），（（α））B是电路模型所展示的量子门操作（下标B表示门操作的对象为qubitB）。接下来展示｜L3〉ABC中的等价规律，如图 4所示。

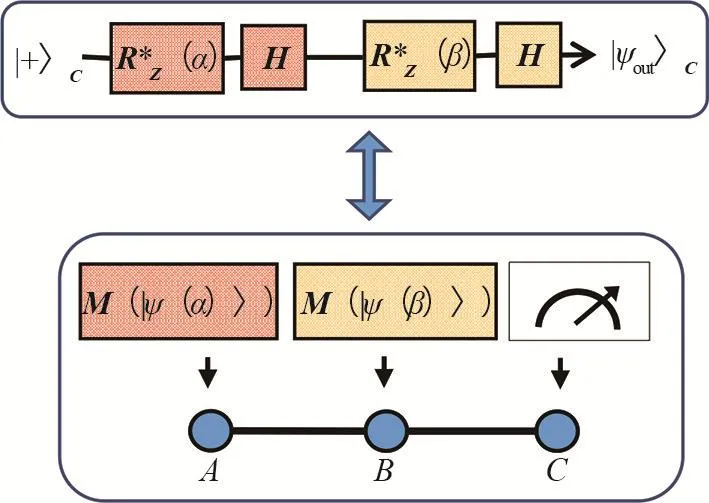
图4 电路模型与等效的对｜L3〉ABC的测量方案

与图3类似，图4上方是对qubitC进行量子门操作，即对｜＋〉C依次进行门操作

下方蓝框表示的是对图态｜L2〉AB进行测量，图中的M（｜ψ（α）〉）表示 qubitA在测量后坍缩为｜ψ（α）〉A，M（｜ψ（β）〉） 表示 qubitB在测量后坍缩为｜ψ（β）〉B，由表达式（21）可知，相应的qubitC坍缩到图中的等价性主要展示了测量和门操作之间的等价性，并没有体现相位因子

对于图4，结合式（21），还可以看出，对A、B的测量顺序并不会影响最终的结果。当A和B都被测量完，C就会坍缩到特定的态，所等价的经历的门操作总是先对应“对A的测量”，再对应“对B的测量”，而与A、B测量的先后顺序无关。

也可以简单考虑一下测量结果和测量基之间的关系。

若选用测量基M（φ）＝｛｜0〉＋eiφ｜1〉，｜0〉－eiφ｜1〉｝ 测量 qubitA，用M（｜ψ（α）〉） 表示测量结果为｜ψ（α）〉A，可以知道测量结果只有两种可能，即｜ψ（α）〉A＝｜ψ（φ）〉A或｜ψ（α）〉A＝｜ψ（φ－π）〉A。

同样，若选用M（θ）＝｛｜0〉＋eiθ｜1〉，｜0〉－eiθ｜1〉｝测量 qubitB，用M（｜ψ（β）〉） 表示测量结果为｜ψ（β）〉B， 同样，也只有两种可能的结果：｜ψ（β）〉B＝｜ψ（θ）〉B或｜ψ（β）〉B＝｜ψ（θ－π）〉B。

其实，并不需要考虑测量基，只需要将测量后坍缩到的态写成｜ψ（γ）〉的形式，求出γ，就得到了该测量所等价的门操作（γ）的具体表达。并且，该量子门操作是作用在线性图态的末端的qubit上。

综上，图3和4展示出对线性图态的测量等价于对末端量子比特进行了相应的门操作。由于其等价规律很优美，自然想到将其推广到高维线性图态的情况，见第3节（采用数学归纳法证明了本文的猜想）。

3 等价关系的一般性证明

本节将在｜L2〉和｜L3〉的基础上，采用数学归纳法，证明任意n-qubit线性图态（n≥2）都满足该等价关系。

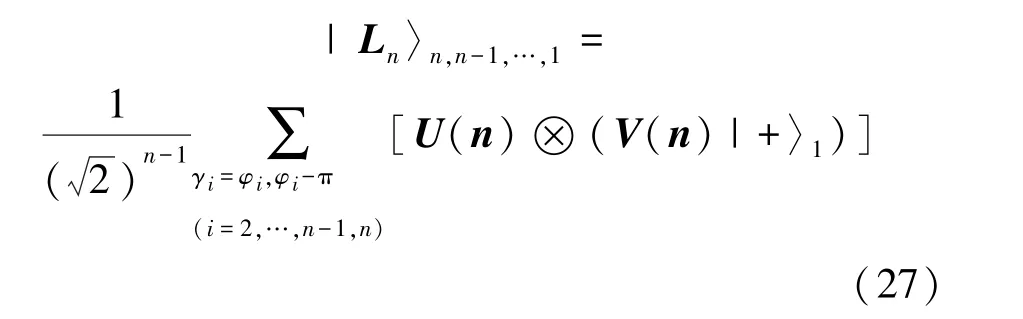
如图5所示，为了便于证明本文的猜测，即验证等式（27）在n≥2时都成立，将图态的量子比特由右向左编号，如图5所示。

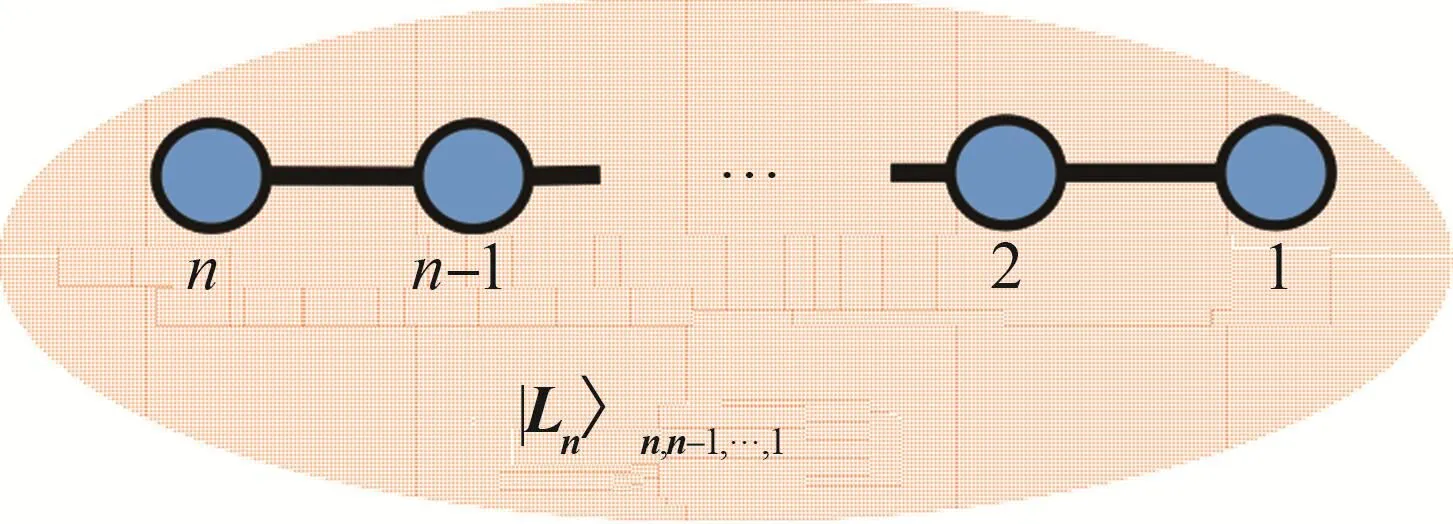
图5 线性态｜Ln〉n，n-1，…，1

接下来，采用数学归纳法，验证其猜测，即验证等式（27）对任意的n≥2都成立。

（1） 当n＝2时，由式（20）得

由此可知，n＝k＋1时，等式（27）依然成立。

综上，根据数学归纳法可知，表达式（27）对任意的n≥2的n-qubit的线性图态都成立。

4 结束语

本文主要研究线性图态中量子测量与量子门操作的等价关系，通过对二量子比特图态｜L2〉AB和三量子比特图态｜L3〉ABC进行分析，发现对图态的量子比特的测量等价于对线性图态中末端量子比特进行了量子门操作，并将该等价关系推广到任意线性图态。最后，通过数学归纳法，证明了该等价性在任意的n量子比特的线性图态（n≥2）中都成立。本工作研究了所有线性图态的一般规律性，对未来研究图态在量子计算和量子通信中的应用提供一定参考价值。