特殊形式和结构的MSP问题NP完全性研究

马兰 刘新 朱哲

摘 要：针对一个NP完全问题，即MSP问题，研究其问题的结构性质，猜想特殊的结构可以使其算法证明得到简化。以简化证明为导引，提出一种特殊形式和结构的MSP问题。而约束了形状的特殊形式和结构的MSP问题如果不具备NP完全性，会极大影响进一步简化算法证明的研究意义。因此，提出的特殊形式和结构的MSP问题进行了NP完全性质证明。类比对SAT问题开展研究时，同样开展特殊结构的2-SAT问题、3-SAT问题、k-SAT、max-SAT问题研究，特殊形式和结构的MSP问题同样具有重要意义，并进一步推动原问题的研究。

关键词：MSP问题;多项式归结;NP完全性

Abstract：An NP-complete problem named MSP problem was found to be structurally reducible. The reduction can simplify the algorithm proof of MSP problem. So we present a MSPproblem with a special form and structure （the special MSP， for short）. However， if the special MSP is not NP complete.The subsequent research on simplified proof will be meaningless， so we present the NP-complete proof of the special MSP in this paper. The research of the special MSP is just like when we study SAT problems， we also study SAT problems with special structure such as 3-SATproblems， 2-SAT problems， k-SAT problems. Similarly， the special MSP problem is of great significance， and further promotes the research of the MSP problem.

Key words：MSP problem;polynomially reduction;NP-comlete problem

MSP问题是一个NP完全问题[1]。NP完全问题在科学研究和实际应用中广泛存在，是理论计算机领域最重要的问题。许多基础性问题表现为NP完全问题，如0-1整数规划、分团问题、图着色问题、最小顶点覆盖，以及众多工业中求最优解问题等[2]。NP完全问题遍布人工智能、数据库、程序语言、计算机网络等计算机科学领域[3]。

一个问题的NP完全性研究一直是理论计算机领域重要的方向。上世纪70年代初Cook[4]给出了NP完全问题的定义，并证明了第一个NP完全问題—SAT问题。接着，Cook还证明了3-SAT问题、团问题是NP完全的。几乎同一时间，Leonid Levin[5]证明了集合覆盖，及拼砖问题等是NP完全的。随后Richard Karp[6]进一步明确了NP完全的概念，并发展了多项式归结技巧，极大推动了NP完全问题的研究，越来越多的问题被归入NP完全类。

NP完全问题的研究在七八十年代达到高潮，随后趋于平静。MSP问题的最早提出实际可追溯到2010年[7，8]，随后陆续有围绕MSP问题的研究发表。如SAT问题归结到MSP问题[9]，子集和问题归结到MSP问题[10]，着色问题和子图同构问题归结到MSP问题[11]等。

2020年发表的文献全面论述了MSP问题的准确定义、多项式时间算法、算法的正确性证明及将哈密顿图判定问题归结到MSP问题，使MSP问题一度成为NP完全问题研究中的新热点。主要内容是对任意输入的图G，文献[1]的算法将计算得到一个判据，并依据判据是否为空，判定一种被称为“简单路径”的路径的存在性。为了归纳证明算法的正确性，文献[1]给出了长篇幅的正确性证明。证明利用了MSP问题的结构特性，通过归纳法，分情况讨论，逐级分析。

在对证明的分析过程中发现，若MSP问题的结构上增加一定的限制条件，可能使证明过程中一些需要重点论述的部分得到简化，那么限制结构以后的MSP问题的算法证明将变得简单。

类比SAT问题。SAT问题被限制结构成为2-SAT、3-SAT以后，3-SAT在保持了NP完全性的同时，发挥其结构更简的优势，应用更广，如今，3-SAT在逻辑推理、人工智能的专家系统、数据库维护和检索、VLSI设计及检测等领域有广泛的应用，但同样被限制了结构的2-SAT问题却不具备NP完全性。

限制了结构的MSP问题被称为特殊结构的MSP问题。但特殊结构的MSP问题是否仍然保留了NP完全性，需要进一步证明，否则，对特殊结构的MSP问题的讨论将缺乏意义。所以主要工作包括两个部分。一是提出一类特殊结构的MSP问题，二是证明提出的问题具备NP完全性质，目的是为寻找文献[1]的算法的简化提供新的研究方向。

1 特殊形式的MSP问题相关定义

下面是关于MSP问题相关定义的描述。

定义1：G=V，E，S，D，L，λ>表示加标多级图，其中，V表示顶点集合，E表示边的集合，S表示多级图中的唯一源点，D表示多级图中的唯一汇点，L表示多级图中的点的级别，〈u，v，l〉表示一条起点为u，终点为v，且v所在级为l的有向边，λv表示顶点v的边集。

加标多级图中每一级都是相互独立的，且不相邻的两级的顶点之间不存在直接相连的边。多级图中所有的边都是有向边，方向由下面一级指向上面一级。每级都有一个及以上的顶点，且每个顶点都有指定的顶点边集。点和边的数量和层级决定了多级图的形状和结构，而边集实际上是一种“控制”。

由简单路径的定义可知，简单路径是从源点S经过各个级中的某个顶点到达汇点D的路径，且每个顶点的边集都包含路径中顶点所在层级以下的路径上所有的边。

判断一个加标多级图中简单路径的存在性。称为MSP问题，即多级图简单路径（Multistage-graph Simple Path）问题。

因为L-2级的点出度大于1，那么“撕裂”操作（如图1）使得原来L-2级的点分为多个部分，在算法的计算过程中，CompESS1，D，RE≠φ的要求可能得不到满足，归纳假设无法继续进行。基于这个考虑，文献[1]关于算法证明部分，要求了对输入的图和输入的边集ESS，必须满足一个条件，即ESSL-1：L=EL-1：L。使得“撕裂”操作不会减少解。

但是这个要求ESSL-1：L包含更多的边的条件，给压缩过程（如图2）带来了问题，会使得压缩后出现增加解（即增加简单路径）的情况，于是文献[1]对于压缩得到的图又进行了一定改造，将可能增加的包含于ESS的简单路径消除。证明也随之变得复杂。

经过对证明过程的研究，可以猜想对于一些特殊结构的图，问题会变得简单。例如，对于任意顶点b，如果b是多入度点时，b一定是单出度点，那么，对“撕裂”后的新图G1，Comp（ESS1，D，R（E））≠？的要求完全可以满足，因为在这样的特殊结构下，从v到D只有一条路径。因此，后续的修改就不再必要。在这种特殊结构下，在证明中省略一些性质，可以大大简化讨论。

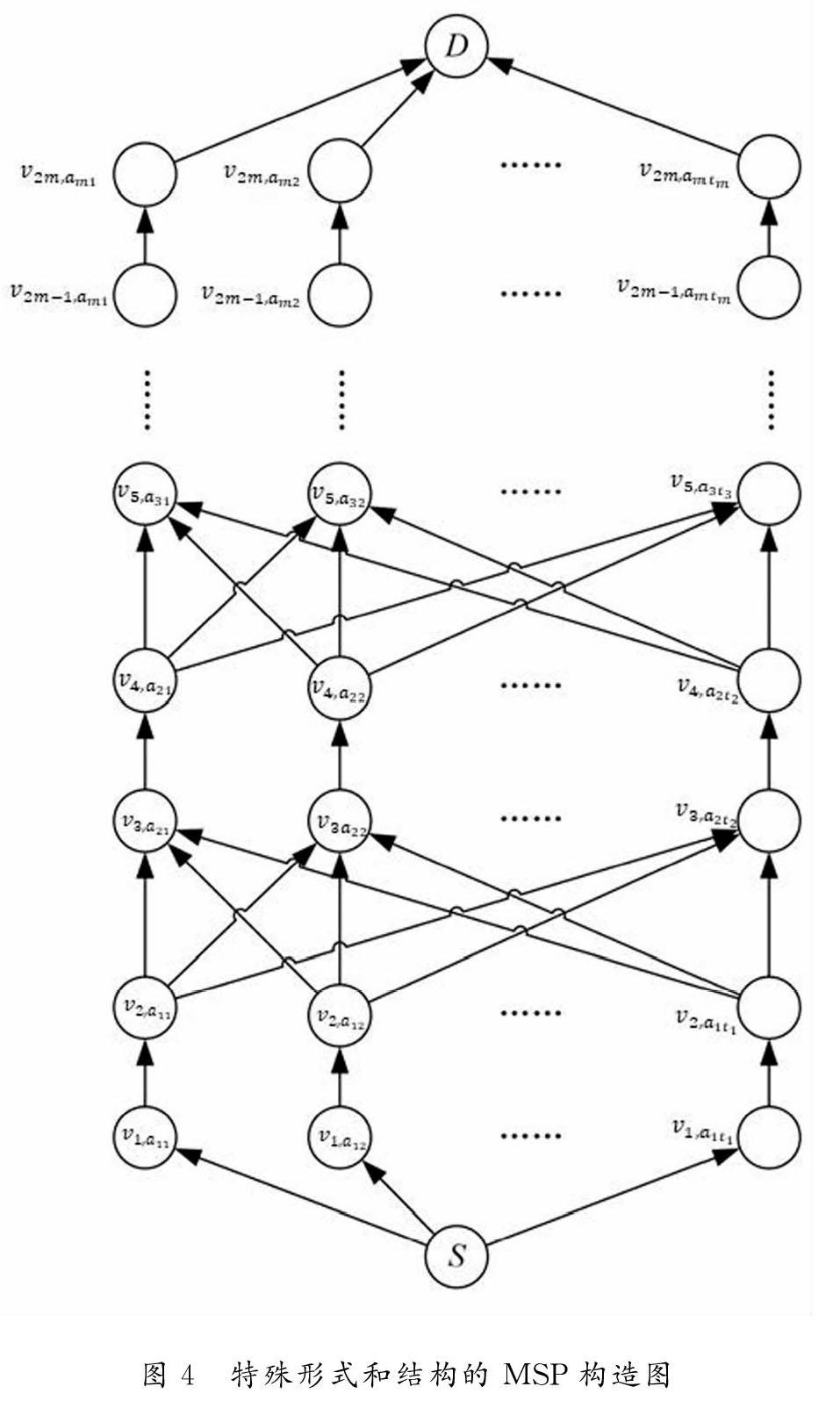
基于这个想法，提出特殊形式的MSP问题。定义如下：

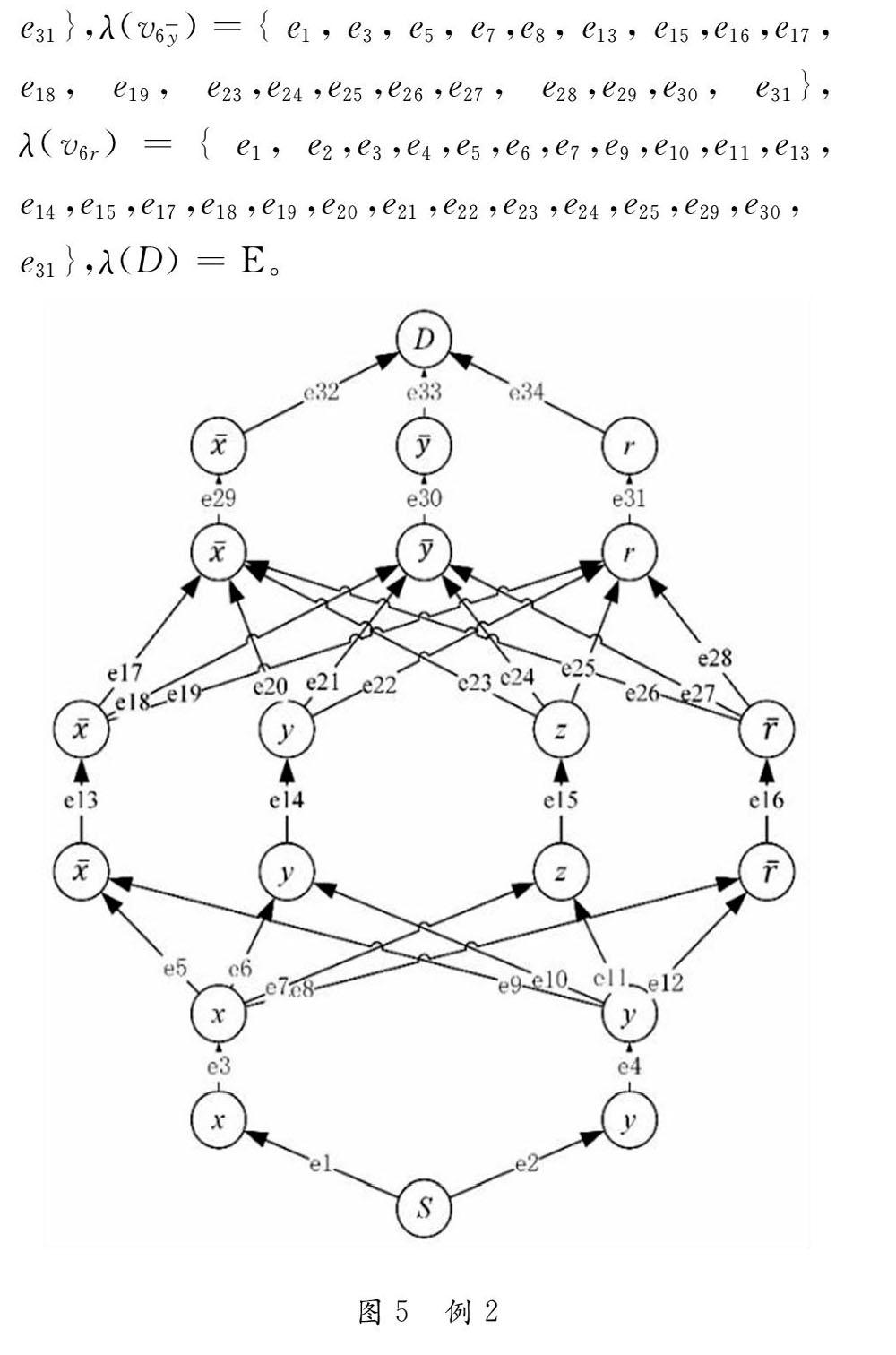
经计算得CompλD，D，RE≠φ，该图存在简单路径。

由例1可以看出，特殊形式和结构的MSP问题与MSP问题在基本概念的定义、简单路径求解、约束关系等方面都是相同的。只有结构方面，特殊结构和形式的MSP问题中，奇数层级指向偶数层级的边连接的两级的顶点，点与点数量相等且一一相连。在这种结构下，多入度且多出度的点不复存在。因此，这种特殊结构下MSP问题算法的证明可能会变得简洁。但只有提出的特殊结构的MSP问题仍然具备NP完全性质才能进行这样的研究。如果不具备NP完全性质，研究这些特殊结构的MSP问题的多项式时间算法的意义将大打折扣。

2 特殊形式的MSP问题的NP完全性研究

COOK 定理之后，要证明一个问题Q是NP完全问题分为三步：

（1） 证明问题Q属于NP。

（2） 选择一个已知的 NP完全问题Q'。

（3） 构造从 Q'到Q的多项式变换函数 f。

首先是第一步，特殊形式的MSP问题显然是NP问题，只要猜测一条路径并代入验证是否是简单路径即可。第二步和第三步，可以选择SAT问题作为已知的NP完全问题，并构造SAT问题归结到特殊形式的MSP问题的多项式变换函数。

SAT问题是指对于一个给定的、由n个不同命题变元组成的集合的M={x1，x2……xn}，以及M上的一个合取范式φ，是否存在对M中命题变元的一组为TRUE或FALSE的指派，使得φ的值为真。选择SAT问题的原因是，SAT问题中合取范式的子句和文字的构造，与多级图中的层级以及每级的顶点的构造有异曲同工之妙。同时，对于SAT问题中的合取范式，含有互补文字的子句之间存在约束，而对于MSP问题中的多级图，有着顶点边集的约束，以及不同层级之间不存在直接相连的边的约束。因此，SAT问题与MSP问题结构与约束都十分相似。因此选择SAT问题作为已知的NP完全问题，并构造SAT问题归结到特殊形式的MSP问题的多项式变换函数。

根据MSP问题和SAT问题的相似性，将合取范式中的子句转化为多级图中的层级，子句中的文字用每级的顶点表示，由于合取范式φ中有文字存在互补关系的约束条件，将多级图顶点的边集设置为除去所有与该顶点互补的顶点相连的边之外的所有的边的集合的任一子集。记为λvilEe∨e∈E，e包含顶点vjl，1≤j≤L}。

2.1 SAT问题归结到特殊形式和结构的MSP

特殊形式的MSP问题显然是NP问题，任意非确定图灵机只要猜想一条从源点S到汇点D的路径，再验证是否为简单路径即可，这种猜想和验证均在多项式时间内完成，因此是NP问题。SAT问题可以在多项式时间O（K3）内归结到这种特殊形式的MSP问题，因此，综上所述，特殊形式的MSP问题是NP完全问题。

2.2 SAT问题归结到特殊形式和结构的MSP问题实例

计算得到CompλD，D，RE≠φ，即图中存在简单路径，也就是说存在一组对变量x，y，z，r的TRUE或FALSE的指派，使得F为真。

3 结 论

定义了一種特殊形式和结构的MSP问题，并将SAT问题归结到了特殊形式和结构的MSP问题。同时给出了特殊形式和结构的MSP问题的NP完全性证明。这将为MSP问题的研究提供新参考。同时，这种归结的产生，也为MSP问题算法正确性证明提供一种新思路，即通过特殊形式和结构的MSP问题来归纳证明。关于这方面，已经做了初步的工作，针对文献[1]中提出的算法，编程实现并进行特殊形式和结构的MSP问题实例测试，采用归纳假设的思路对文献[1]证明过程进行重写等。

参考文献

[1] 姜新文.哈密顿图判定问题的多项式时间算法[J].计算机科学，2020，47（7）：8-20.

[2] FORTNOW L. The status of the P versus NP problem[J]. Communications of the ACM， 2009， 52（9）：78-86.

[3] COOK S. The importance of the P versus NP question[J]. Journal of the ACM （JACM）， 2003， 50（1）： 27-29.

[4] COOK S. The complexity of theorem proving procedures[J]. Theory of Computing， 1971， 151-158.

[5] LEVIN L A. Universal sequential search problems[J].Problemy Peredachi Informatsii，1973，9（3）：115-116.

[6] KARP R M. Reducibility among combinatorial problems[C].Complexity of Computer Computations， 1972， 85-103.

[7] JIANG Xin-wen， PENG Li-hong， WANG Qi. MSP problem：its NP-completeness and its algorithm[A]. 2010 Proceedings of the 5th International Conference on Ubiquitous Information Technologies and Applications，2010.

[8] 姜新文，王琪，姜子恒.Z-H算法正确性证明第四次改写[J].计算技术与自动化，2010，29（3）：35-48.

[9] 樊硕，姜新文.SAT问题可多项式归结到MSP问题[J].计算机科学，2012，39（11）：179-182.

[10]JIANG Xin-wen， LIU Wan-wei， WU Tian-jun， et al. Reductions from MSP to SAT and from SUBSET SUM to MSP[J]. Journal of Computational Information Systems， 2014， 10（3）： 1287-1295.

[11]吴添君，姜新文.MSP问题NP完全性研究[J].计算机科学， 2015， 42 （7） ：12-14.

[12]姜新文，吳添君，李鹏坤，等.MSP问题的一个求解算法[J].计算技术与自动化，2016，35（1）：60-70.