贝叶斯网络在配电网可靠性评估中的应用

刘骁暘，张 鹤

应用研究

贝叶斯网络在配电网可靠性评估中的应用

刘骁暘，张 鹤

（海军装备部驻上海地区第一军事代表室，上海 201913）

贝叶斯网络在电力工程有效性和可靠性研究、电源品质分析、风险评估、电力监测和故障诊断中有重要的应用。提出了基于条件概率的贝叶斯理论方法如何在不同配电网节点和电力供应链结构中进行具体应用。根据相关实际系统，可以用RBD（可靠性框图）、割集或系集方法、事件树或失效树技术来构建贝叶斯网络。

条件概率理论 贝叶斯网络 可靠性 配电网 节点结构

0 引言

系统可靠性和实用性是重要的研究领域。贝叶斯网络（BN）能对此进行有效的分析[1～9]。从最初Judea Pearl[10]和F. V. Jensen[11]建立动态贝叶斯网络（DBN）的时间序列模型到目前J. B. Dugan[12]建立故障容许计算系统和故障树的动态故障树模型，以及故障容许数字系统可靠性分析的Markov模型[13]，学者们发表了很多关于电力系统及其子系统或设备可靠性的文章。Chun Su和Ye-qu Fu发表了基于贝叶斯网络考虑风速影响的风力涡轮机可靠性分析[14]，其中应用了与连续变量离散相结合的近似推理算法来获得风力涡轮机及其零件的可靠性指标。L. Gao， Y. Zhou， C. Li和L. Huo[15]发表了一篇基于BNs进行含分布式发电的分布式系统可靠性评估的文章，指出不仅可以计算分布式系统可靠性指标，还可以评估各设备或零件对系统可靠性的影响。Duan Zhou[16]在他关于BNs在系统可靠性中应用的MSc理论中，建立了含从常数到连续时间事态多状态节点的两组模型来应用和对比贝叶斯网络和经典故障树方法，扩展模型离散了连续变量并提供了随时间变化的失效相关概率分布。Munteanu F.和Nemes C.[17]从相关因素太阳能和风力两个可再生资源的详细分析中提出了节点电源品质和实用性评估的可信网络应用，同时也开发了可用于从包括可再生能源和主要电网零件的角度评估节点品质供应的相关贝叶斯模型结构。文献[18]包含了可以通过BN建模的设计细节。Mahadevan S在文献[19]中提出了一种在结构系统可靠性重新评估中应用贝叶斯网络的方法，方法中包含了大型结构的两大重要特征：一是失效的多步骤，二是与零件等级极限状态的相关性。最终，Adrian Darwiche编写了一部极为实用的教材来揭示BN中的计算背景，自动推理和概率如何演化。

本文聚焦于不同节点结构进行BN实用性分析和可靠性评估。

1 贝叶斯网络自动推理可靠性计算背景

概率论中有三大公理：

1）0≤≤1；

2）=1代表必然事件概率；

如果事件和事件互斥，则

如果、不互斥，则

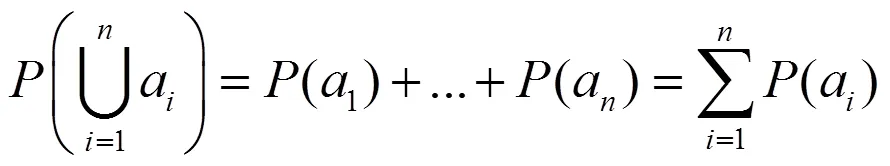
3）概率计算的基本表示法则为：

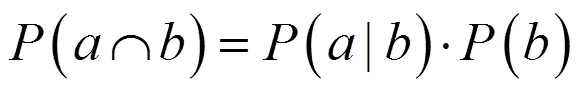
从式(1)可以看出，如果给定先验概率和的概率，且为正，则后验概率的贝叶斯理论计算公式为：

归一化因子可用下式计算：

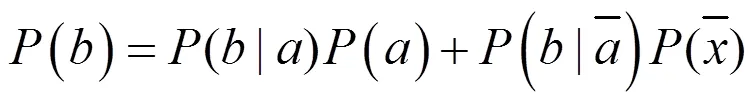
贝叶斯理论的广义形式由下式给出[20～21]：

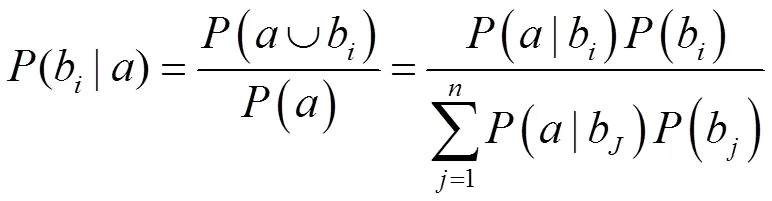
其中（）和（）≥0，以及b是两两互斥事件。

由式(5)，可以由计算得出：

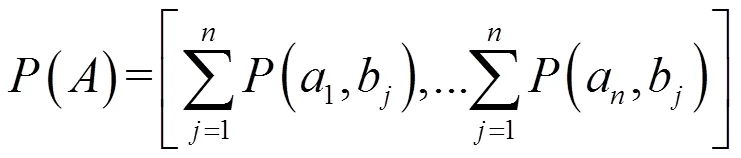
方程(6)可以简化为：

其中在贝叶斯理论中为从中边缘化或淘汰。下面我们将把贝叶斯基本理论应用到实用性评估与该主题相关的更多实例中，尤其是配电网节点结构的可靠性中。

2 一般配电网节点结构的贝叶斯网络实用性评估

图1 一种典型桥接节点结构

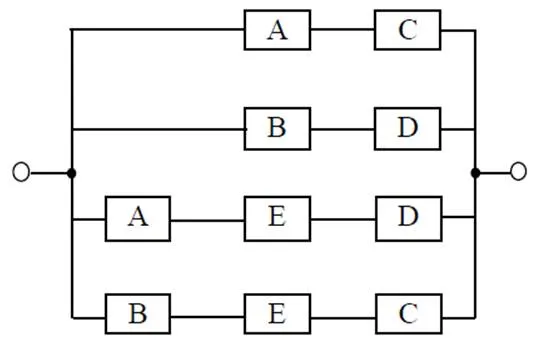
图2 分段单总线结构的最小系集

（A,B,C,D,E是等效串行可靠性元件）

图1给出了节点的单分段总线结构。图2给出了等效可靠性块和最小系集图，成功的状态包括AC或BD或AED或BEC零件处于良好的状态并有效连接。假设所有零件从给定概率可靠性可靠点角度有2种状态（成功或失效），相应的贝叶斯网络如图3所示。

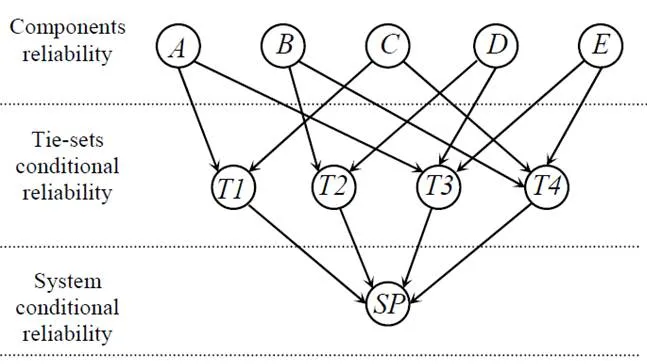
图3 中结构可靠性评估的贝叶斯网络

图4 基于系集的贝叶斯网络桥接节点结构可靠性计算

图4显示了从两个边缘状态（up和down）变量概率（分别为0.85和0.15）开始的割集和系统概率的结果。图5展示了一周内纵向耦合器（E）对整个系统可靠性的影响。对元素工作有正面影响。割集技术也用来进行复杂系统的可靠性分析。桥接节点结构的的系集如图6所示。相应的贝叶斯网络如图7所示。其中边缘变量的条件概率和最终结果一致，概率供应都是S=0.9874。正如在系集技术案例中，在边缘变量（父级变量）中使用相同的值，结果如图8所示。

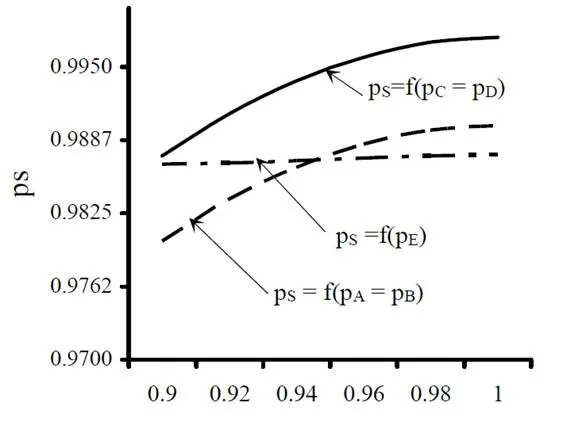
图5 提供公共负载的概率随系集元素概率变化的函数

图6 桥接节点结构的割集

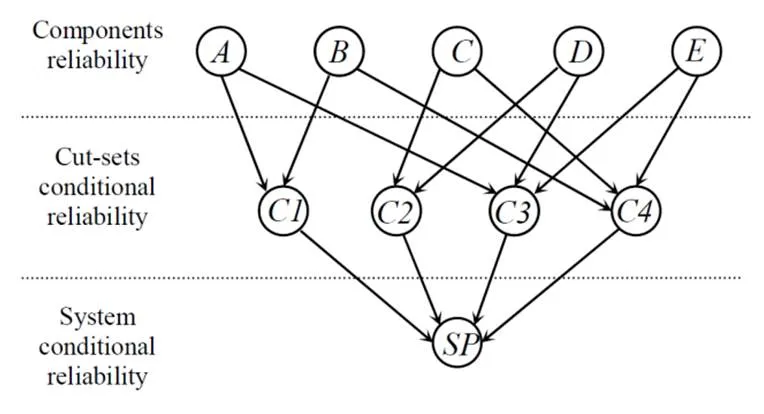
图7 基于割集的贝叶斯网络

图8 使用割集方法的桥接节点结构边缘和条件概率

3 结论

贝叶斯网络是一个用于概率变量驱动系统自动推理的极为通用的工具。它可以根据概率微积分的公理和规则，并基于生成贝叶斯理论进行构造。配电网节点的实用性可以使用贝叶斯网络，基于割集、系集、故障树、事件树或马尔可夫链方法等不同技术，将实际的技术系统转换为相应的贝叶斯网络。本文提出了两个一级节点结构的有效性分析及数值案例研究。

下一步工作是致力于使用数据驱动贝叶斯网进行更为复杂的系统建模：复杂节点结构、多状态断路器、电力转换监视、故障诊断、含随机生成的电网有效性评估和可再生能源的高度引入。

[1] 张燕. 贝叶斯网络概述[J]. 科教导刊. 2017, 32 (11): 290.

[2] Wagner A. How to reconstruct a large genetic network from n gene perturbations in fewer than n2 easy steps [J]. Bioinformatics, 2001(17): 1183-1197.

[3] Robbins, H.&S. A. Monro. Stochastic approximation method [J]. Annals of Mathematical Statistics, 1951(22): 400-407.

[4] Pearl, J. Probabilistic reasoning in intelligent systems[J]. Morgan Kaufinann, 1988:1-86.

[5] 胡春玲. 贝叶斯网络的结构学习算法研究[D]. 合肥:合肥工业大学, 2006.

[6] 曹冬明, 张伯明, 邓佑满, 田田. 一种新型故障定位方法的研究[J]. 电力系统自动化, 1999, 23(07): 12-14.

[7] 李伟生, 王宝树. 实现规划识别的一种贝叶斯网络. 西安电子科技大学学报(自然科学版), 2002, 29(06): 741-744.

[8] 邓勇施, 文康, 陈良州.基于模型诊断的贝叶斯解释及应用[J]. 上海交通大学学报, 2003, 37(01): 5-8.

[9] 李明, 邓家梅, 曹家麟. 基于贝叶斯网络的串行译码方法[J]. 通信技术, 2001, 115 (04):38-40.

[10] Pearl J. Graphical models, causality, and intervention[J], Statistical Science, Vol. 8, no. 3: 266–273.

[11] Jensen F. (2001). Bayesian Networks and Decision Graph, Springer.

[12] Dugan J B, Bavuso S J. and Boyd M A. Dynamic Fault Tree models for Fault Tolerant Computer Systems, IEEE Trans. Reliability, 1992. 41, 363-377.

[13] Dugan J B, Bavuso S J. and Boyd M.A. Fault-trees and Markov models for reliability analysis of fault-tolerant digital systems, Reliability Engineering and System Safety 1993, 39. 291-307.

[14] Su C, Fu YQ. Reliability assessment for wind turbines considering the influence of wind speed using Bayesian network[J]. Eksploatacjai Niezawodnosc –Maintenance and Reliability 2014, 16 (1): 1–8.

[15] Gao L. Zhou Y, Li C, Huo L. Reliability assessment of distribution systems with distributed generation based on bayesian networks[J]. Engineering Review, vol. 34, Issue 1, pg.55-6, 2014.

[16] Duan Z, The application of bayesian networks in system reliability[J]. Master of Science Degree Thesis. Arizona State University, Dec. 2014.

[17] Munteanu F, Nemes C. Belief networks utilization for nodal power quality and availability assessment. U.P.B. Sci. Bull, Series C, 2012. 74, (1), ISSN: 205-222.

[18] Munteanu, F, Alexandra Ciobanu, Nemes, C. From technical design structures to bayesian networks in power engineering. paper ID 02, Section Power Systems, accepted for publication in ICATE 2016 Conference Proc. Of. Craiova, Oct. 6-8 2016.

[19] Mahadevan S, Zhang R., Smith N. Bayesian Networks for System Reliability Reassessment[J]. Structural Safety Journal, Elsevier, 23 (2001), p. 231-251. ISSN: 0167-4730.

[20] Darwiche Modeling and Reasoning with Bayesian Networks[M]. Cambridge University Press. ISBN 978-0521-88438-9, 2009.

[21] Bolstad M W. Introduction to Bayesian Statistics. J Wiley & Sons, Inc., 2007. ISBN 978-0-470-14115-1.

[22] Kjerulff U, Madsen A. Bayesian networks and influence diagrams: a guide to construction and analysis. Springer, 2ndedition 2013, 382 pg. ISBN-13: 978- 1461451037.

[23] 张燕. 贝叶斯网络的构建过程[J]. 科教. 2018, (7):190。

Application of Bayesian Network in Reliability Evaluation of Distribution Network

Liu Xiaoyang, Zhang He

(The First Military Representative Office of Naval Equipment in Shanghai, Shanghai 201913, China)

TM732

A

1003-4862（2021）09-0047-03

2020-12-04

刘骁暘（1989-）研究方向：电气工程，船舶电力系统。Email：zhangyuelin24@hotmail.com