成对型复微分差分多项式的零点与唯一性

刘 凯，高迎春

(1.南昌大学数学系，江西 南昌 330031)

1 引言及主要结果

本文假设读者熟悉亚纯函数值分布理论[1-2]的基本概念和符号。例如：特征函数T(r,f),计数函数N(r,f)和均值函数m(r,f)。函数增长级ρ(f)和超级ρ2(f)定义如下：

若亚纯函数a(z)满足T(r,a(z))=o(T(r,f))=S(r,f),r→∞至多除去一个具有有限对数测度的例外集，则称函数a(z)为f(z)的小函数。

亚纯函数的零点研究是值分布理论的一个重要课题，代数学基本定理说明任何非零多项式都存在零点，经典的Picard定理说明超越整函数f(z)至多有一个有限的Picard例外值，即f(z)-a有无穷多个零点至多有一个例外的a值；而超越亚纯函数至多有两个有限的Picard例外值。Hayman[3]研究了复微分多项式f(z)nf′(z)-a的零点个数问题，此类问题是研究复微分多项式零点的重要起点，后续很多亚纯函数零点问题、唯一性问题和正规族理论的研究都受此问题的启发。

定理A[3，定理10]设f(z)是超越整函数且n≥2为正整数，a是非零常数，则f(z)nf′(z)-a有无穷多个零点。

Clunie[4]证明了当n=1时定理A也是正确的。那么，如果f(z)是超越亚纯函数，情况会如何呢？Hayman在文献[3]中提出如下猜想:

Hayman猜想：设f(z)是超越亚纯函数且n是正整数，a是非零常数，则f(z)nf′(z)-a有无穷多个零点。

事实上，Hayman[3]得到了下面结果：

定理B[3]设f(z)是超越亚纯函数且n≥3是正整数，a是非零常数，则f(z)nf′(z)-a有无穷多个零点。

在众多数学家的努力下，Hayman猜想现已被完全证明，其中Mues[5]证明了定理B中n=2的情况，Bergweiler和Eremenko[6]，Chen和Fang[7]以及Zalcman[8]分别证明了n=1的情况。Hayman猜想说明对于特殊类型的亚纯函数f(z)nf′(z)的Picard例外值仅可能为0。目前，与Hayman猜想有关的问题研究依然十分活跃。2007年，Laine和Yang[9，定理2]首次研究了Hayman猜想的差分版本，即复差分多项式的零点分布，并得到了下列结果：

定理C设f(z)是有穷级超越整函数且a和c是非零常数，则当n≥2时，f(z)nf(z+c)-a有无穷多个零点。

之后，各种类型的复差分多项式的零点和值分布问题得到了广泛研究，例如：Liu和Yang[10，定理1.4]研究了f(z)n[f(z+c)-f(z)]-p(z)的零点分布情况，其中p(z)是一个多项式。Luo和Lin[11，定理1]将定理C中常数a替换成了f(z)的小函数a(z)，将f(z)n替换成了f(z)的多项式，并得到了下面的结果：

定理D设f(z)是有穷级超越整函数,c是非零常数，an(≠0),an-1,…,a0是常数，P(z)=anzn+an-1zn-1+…+a1z+a0，且P(z)有t个判别的零点，如果n>t，则P(f)f(z+c)-a(z)有无穷多个零点，其中a(z)为f(z)的非零小函数。

如果定理C中有穷级超越整函数替换成超级小于1的超越亚纯函数，Liu，Liu和Cao[12]证明n≥6时定理C成立，Wang和Ye[13]改进到n≥4，Liu，Liu和Cao[12]构造反例说明n≤3时定理C不成立。关于定理D的亚纯情况及其他类型微分差分方面的研究可见专著Liu，Laine和Yang[14,第2章]。在上述的研究中，所有的研究思路都集中在函数及其本身的微分差分多项式的研究上。而构建成对型的问题是Hayman猜想有趣的创新，例如：设f(z)和g(z)是超越亚纯函数，a为非零常数，那么能否得到fn(z)g′(z)-a与gn(z)f′(z)-a二者之一必有无穷多个零点？如果能证得，那么取f=g便可以得到定理A，B的结果。基于上述的研究思路，Gao和Liu[15]首次研究了成对型微分差分多项式f(z)nL(g)-a(z)和g(z)nL(f)-a(z)的零点分布情况，其中a(z)是f(z)和g(z)的非零小函数，L(h)可以取高阶导数h(k)(z)，平移h(z+c)，差分h(z+c)-h(z)和延滞微分h(k)(z+c)四种情况。为表述简洁，我们用M表示超越亚纯函数类，M′表示超级小于1的超越亚纯函数类，E表示超越整函数类，E′表示超级小于1的超越整函数类。

Gao和Liu[15]得到了下面的定理：

定理E设f(z)和g(z)是超越亚纯函数，若满足下面的任意一个条件：

ⅰ.当L(h)=h(k)(z)，若h∈M且n≥k+4或者h∈E且n≥3；

ⅱ.当L(h)=h(z+c)，若h∈M′且n≥4或者h∈E′且n≥3；

ⅲ.当L(h)=h(z+c)-h(z)，若h∈M′且n≥5或者h∈E′且n≥3；

ⅳ.当L(h)=h(k)(z+c)，若h∈M′且n≥k+4或者h∈E′且n≥3，

则f(z)nL(g)-a(z)和g(z)nL(f)-a(z)至少一个有无穷多个零点，a(z)是f(z)和g(z)的非零小函数。

文[15]中，Gao和Liu进一步考虑了相应的分担公共值的唯一性问题，得到了下面的定理：

定理F设f(z)和g(z)是超越亚纯函数，a(z)是f(z)nL(g)和g(z)nL(f)的CM公共小函数，其中a(z)是f(z)和g(z)的非零小函数。如果下面的任意一个条件满足：

ⅰ.当L(h)=h(k)(z)，若f，g∈M且n≥3k+16或f，g∈E且n≥8；

ⅱ.当L(h)=h(z+c)，若f，g∈M′且n≥16或f，g∈E′且n≥8；

ⅲ.当L(h)=h(z+c)-h(z)，若f，g∈M′且n≥19或f，g∈E′且n≥8；

ⅳ.当L(h)=h(k)(z+c)，若f，g∈M′且n≥3k+16或f，g∈E′且n≥8

则有f(z)nL(g)=g(z)nL(f)或者f(z)nL(g)g(z)nL(f)=a(z)2。

注当L(h)取特殊情况时，可以得到f和g的关系，可见[15]。

本文将考虑具一般形式成对型微分差分多项式P(f)L(g)-a(z)和P(g)L(f)-a(z)的零点情况，其中P(z)为n次多项式有t个判别零点，且有t1个单零点和t2个重零点(t1+t2=t)，记Γ0=t1+2t2。设P(z)=a(z-z1)s1(z-z2)s2…(z-zt)st(s1+s2+…+st=n)。考虑以下三种不同的L(h)的情况：

D(h)=akh(k)(z)+ak-1h(k-1)(z)+…+a1h′(z)+a0h(z)(k≥1)

(1.1)

Q(z,h)=amh(z+cm)+am-1h(z+cm-1)+…+a1h(z+c1)+a0h(z+c0)

(1.2)

D(z,h)=amh(km)(z+cm)+…+a1h(k1)(z+c1)+a0h(k0)(z+c0)

(1.3)

这里c0,…,cm为互相判别的复数且ai为常数。记kM=km+km-1+…+k0+m+1。

定理1.1假设P(z)如上定义且下列条件之一满足：

1.L(h)=D(h(z))，若h∈M且n≥t+k+3或者h∈E且n≥t+2；

2.L(h)=Q(z,h)，若h∈M′且n≥t+m+3或者h∈E′且n≥t+2；

3.L(h)=D(z,h)，若h∈M′且n≥t+kM+2或者h∈E′且n≥t+2；

则P(f)L(g)-a(z)和P(g)L(f)-a(z)至少有一个有无穷多个零点，a(z)是关于f(z)和g(z)的非零小函数。

定理1.2设f(z)和g(z)是超越亚纯函数，若a(z)是P(f)L(g)和P(g)L(f)的CM公共小函数，其中a(z)是f(z)和g(z)的非零小函数，且下面的任意一个条件满足:

1.当L(h)=D(h(z))，若f，g∈M且n≥2Γ0+3k+12；

2.当L(h)=Q(z,h)，若f，g∈M′且n≥2Γ0+3m+6；

3.当L(h)=D(z,h)，若f，g∈M′且n≥2Γ0+3kM+4m+5，

则P(f)L(g)=P(g)L(f)或者P(f)L(g)P(g)

L(f)=a(z)2。

如果考虑f(z)和g(z)是超越整函数，利用类似定理1.2的证明方法，可以得到

定理1.3设f(z)和g(z)是超越整函数，若a(z)是P(f)L(g)和P(g)L(f)的CM公共小函数，其中a(z)是f(z)和g(z)的非零小函数，且下面的任意一个条件满足：

ⅰ.当L(h)=D(h(z))，若f，g∈E且n≥2Γ0+4；

ⅱ.当L(h)=Q(z,h)，若f，g∈E′且n≥2Γ0+4；

ⅲ.当L(h)=D(z,h)，若f，g∈E′且n≥2Γ0+4；

则有P(f)L(g)=P(g)L(f)或者P(f)L(g)P(g)L(f)=a(z)2。

2 引理

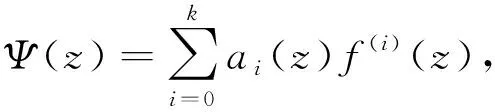
这里ai(z)(i=0,1,…,k)均为f(z)的小函数，则

(2.1)

T(r,Ψ)≤(k+1)T(r,f)+S(r,f)

(2.2)

引理2.2[16]设f(z)为超级小于1的超越亚纯函数，则

T(r,f(z+c))=T(r,f)+S(r,f),N(r,f(z+c))=N(r,f)+S(r,f)

(2.3)

(2.4)

引理2.3若L(h)分别取(1.1)(1.2)和(1.3)，可以得到下面特征函数的估计式：

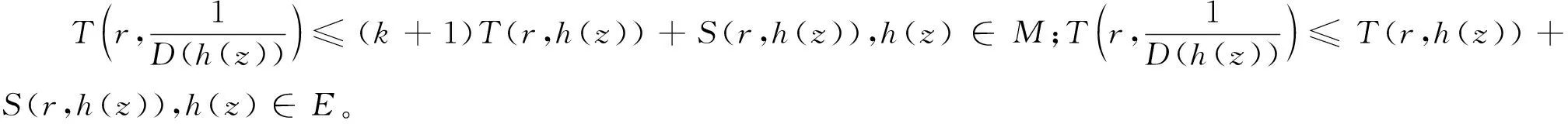
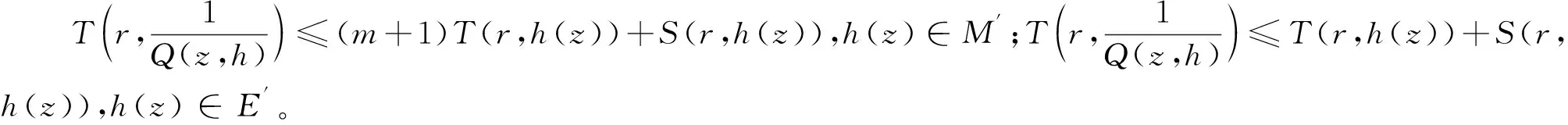
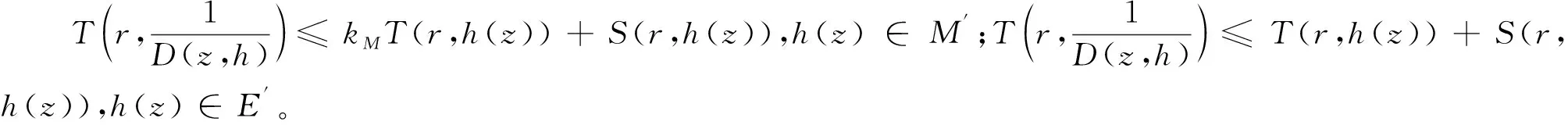
证明情形(1)可由引理2.1和Nevanlinna第一基本定理得到，情形(2)由引理2.2和Nevanlinna第一基本定理得到，情形(3)由引理2.1，引理2.2和Nevanlinna第一基本定理得到。

引理2.4如果f(z),g(z)∈M，则有

nT(r,f)-(k+1)T(r,g)≤T(r,P(f)D(g(z))+S(r,f)+S(r,g)≤nT(r,f)+(k+1)T(r,g)

(2.5)

如果f(z),g(z)∈E，则有

nT(r,f)-T(r,g)≤T(r,P(f)D(g(z))+S(r,f)+S(r,g)≤nT(r,f)+T(r,g)

(2.6)

证明我们仅给出亚纯函数的情况，整函数的情况可类似证明。通过引理2.1可直接证得(2.5)右边的不等式成立，接下来去证明(2.5)左边的不等式。

由引理2.3(1)和Nevanlinna第一基本定理及Valiron-Mohon’ko定理[17，定理2.2.5]可得

利用引理2.4相同的证明方法可以得到下面的两个引理：

引理2.5如果f(z),g(z)∈M′，则有

nT(r,f)-(m+1)T(r,g)≤T(r,P(f)Q(z,g))+S(r,f)+S(r,g)≤nT(r,f)+(m+1)T(r,g)

(2.7)

如果f(z),g(z)∈E′，则有

nT(r,f)-T(r,g)≤T(r,P(f)Q(z,g))+S(r,f)+S(r,g)≤nT(r,f)+T(r,g)

(2.8)

引理2.6如果f(z),g(z)∈M′，则有

nT(r,f)-kMT(r,g)≤T(r,P(f)D(z,g))+S(r,f)+S(r,g)≤nT(r,f)+kMT(r,g)

(2.9)

如果f(z),g(z)∈E′，则有

nT(r,f)-T(r,g)≤T(r,P(f)D(z,h))+S(r,f)+S(r,g)≤nT(r,f)+T(r,g)

(2.10)

设p是正整数且a∈，记

引理2.7[16]设f和g是非常数亚纯函数，α(z)是f和g的非零小函数。如果α(z)是f和g的CM公共小函数，则f和g满足下列三种情况之一：

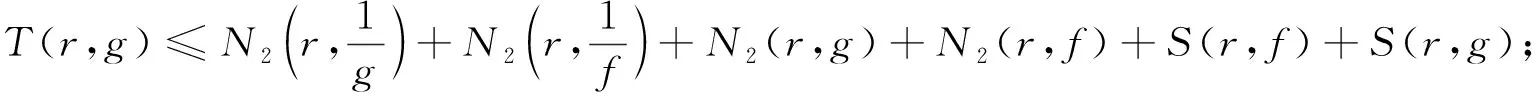
(ⅱ)f≡g；

(ⅲ)f·g=α2。

3 定理的证明

定理1.1的证明设f,g为超越亚纯函数，令F=P(f)L(g)-a(z)，则

nm(r,f)=m(r,P(f))+S(r,f)=

(3.1)

且

nN(r,f)=N(r,P(f))+S(r,f)=

(3.2)

nT(r,f)≤T(r,F(z)+a(z))+

(3.3)

根据F(z)的表达式，我们有

利用Nevanlinna第二基本定理，可以得到

结合上面的不等式以及(3.3)，可得到

(3.4)

下面讨论三种情况：

情形1如果L(g)=D(g(z))，结合引理2.3的(1)，则可以得到

设G=P(g)L(f)-a(z)，利用上述的方法可以得到

因此，结合上面的两个不等式，我们可以得到

所以当n≥t+k+3时，F(z)和G(z)至少有一个有无穷多个零点，即P(f)L(g)-a(z)和P(g)L(f)-a(z)至少有一个有无穷多个零点。

情形2设L(h)=Q(z,h)，结合引理2.3的(2)，利用情形1的方法，可以得到当n≥t+m+3时，P(f)L(g)-a(z)和P(g)L(f)-a(z)至少有一个有无穷多个零点。

情形3设L(h)=D(z,h)，结合引理2.3的(3)，利用情形1的方法，可以得到当n≥t+kM+2时，P(f)L(g)-a(z)和P(g)L(f)-a(z)至少有一个有无穷多个零点。

最后，如果f,g为超越整函数，则利用上述得到(3.4)的基本方法但要去掉极点的计数函数，可以得到

利用引理2.3中整函数时的特征函数估计式，便可得到定理1.1整函数情况下的结果。

定理1.2的证明

情形1设F(z)=P(f)D(g)，G(z)=P(g)D(f)。由于a(z)是F(z)和G(z)的CM公共小函数，利用引理2.2，2.3和2.6的(i)，可以得到

4N(r,g)]+S(r,f)+S(r,g)≤(2Γ0+2k+10)[T(r,f)+T(r,g)]+S(r,f)+S(r,g)

因为n≥2Γ0+3k+12，所以引理2.6的(i)不会发生，因此有P(f)D(g)=P(g)D(f)或者P(f)D(g)P(g)D(f)=a(z)2。

情形2设F(z)=P(f)Q(z,g)，G(z)=P(g)Q(z,f)。由于a(z)是F(z)和G(z)的CM公共小函数，利用引理2.2，2.4和2.6的(i)，可以得到

(n-m-1)[T(r,f)+T(r,g)]≤

因为n≥2Γ0+5m+6，故引理2.6的(i)不会发生。因此有P(f)Q(z,g)=P(g)Q(z,f)或者P(f)Q(z,g)P(g)Q(z,f)=a(z)2。

情形3设F(z)=P(f)D(z,g)，G(z)=P(g)D(z,f)。由于a(z)是F(z)和G(z)的CM公共小函数，利用引理2.2，2.5和2.6的(i)，可以得到

(n-kM)[T(r,f)+T(r,g)]≤(2Γ0+2kM+4m+4)(T(r,f)+T(r,g))+S(r,f)+S(r,g)

因为n≥2Γ0+3kM+4m+5，故引理2.6的(i)不会发生，因此有P(f)D(z,g)=P(g)D(z,f)或P(f)D(z,g)P(g)D(z,f)=a(z)2。

4 讨论

函数型复微分方程的解的性质研究是个有趣的课题，最近的研究可参见[20]，本文中，当f(z)，g(z)为超越整函数时，观察方程

P(f)L(g)P(g)L(f)=a(z)2

(4.1)

由Nevanlinna第二基本定理可知P(z)至多有一个零点，即P(z)=a(z-b)n，其中a为非零常数，b为常数。然而，当f(z)，g(z)为超越亚纯函数时，情况变得复杂。进一步观察方程

P(f)L(g)=P(g)L(f)

(4.2)

如果上面两个方程中L(h)取特殊表达式，比如L(h)=h′(z)或者h(z+c)，部分讨论可参见[15,19]，然而其他情况的研究面临较大困难，即使L(h)=h′(z+c)，都无法从方程f(z)ng′(z+c)=g(z)nf′(z+c)中得到f(z)和g(z)的所有关系式，虽然f(z)=g(z)或者f(z)=tg(z)，tn-1=1满足上述方程。因此，如何从方程(4.1)和(4.2)中寻求f(z)和g(z)准确关系值得深入研究。