负荷勒夫数渐近值解析表达式

周江存，潘尔年

1 中国科学院精密测量科学与技术创新研究院，大地测量与地球动力学国家重点实验室，武汉 430077 2 College of Engineering, Cleveland State University, Cleveland, OH 44115, USA

0 引言

全球水循环是地球表层质量迁移的重要形式，它引起全球水质量在时间和空间的重新分布，会进一步导致地球的变形.该变形主要有三种形式：(1)大气负荷，主要是大气质量的变化对地球的引力作用与压强变化对地表的负载作用(Merriam，1992；Van Dam et al.，1994；Sun and Luo，1998；Guo et al.，2004)；(2)潮汐和非潮汐海洋负荷，主要是海水质量的时空变化对地球的引力作用和对地表的负载作用(Longman，1962，1963；Farrell，1972；Goad，1980；许厚泽等，1982)；(3)陆地水负荷，主要是陆地水的质量变化对地球的引力作用和对地表的负载作用(Zhou et al.，2009).这三种效应可以引起地表几厘米(cm)的位移和数十微伽(10-8m·s-2)的重力变化.在目前高精度的大地测量学研究中，这三种效应都是必须要加以考虑的.对这些效应的模拟，目前已有比较成熟的理论，通常采用负荷质量与负荷格林函数的褶积积分计算获得，其中格林函数是负荷勒夫数或其组合与Legendre函数(或称为球函数)或其导数的乘积的无穷级数求和(Longman，1963；Farrell，1972；Guo et al.，2004).鉴于球函数有解析的递推公式，因此计算格林函数的基础就是计算出负荷勒夫数.

由于格林函数是一个无穷级数的求和，对于一个无穷级数求和的问题来说，高阶勒夫数的高效计算以及格林函数的收敛性如何是数值计算的关键.为了计算高阶的负荷勒夫数，Longman(1963)提出了对变量进行无量纲化的处理；汪汉胜等(1996)通过观察各变量的变化特征提出了r幂因子法；特别地，Pan等(2015)基于合理的假设提出了计算负荷勒夫数的解析解方法；Chen等(2018)基于解析解方法提出了一种称为刚度矩阵的传播矩阵方法来计算超高阶负荷勒夫数，克服传统传播矩阵方法的溢出问题；Zhou等(2019a)运用DVP(dual variable and position)传播矩阵法获得了任意球谐阶数的勒夫数，并提供了相应的MATLAB程序计算不同类型的勒夫数(包括潮汐、负荷、剪切和位错).实际上，这些表征地球在不同力源(如引潮力、地表正应力或剪切应力、以及内部断层的等效体力等)作用下产生变形的勒夫数之间并不完全独立，它们之间的关系可参考潘尔年和丁中一(1986)和Okubo(1993).

为了保证格林函数的收敛，Farrell(1972)给出了负荷勒夫数的渐近值，即当球谐阶数n趋于无穷大时勒夫数的值，然后通过Kummer变换可有效降低截断阶数(约10000阶)并加速格林函数的收敛，从而为能够准确地模拟负荷引起的地球形变奠定了基础.可见，负荷勒夫数渐近值对负荷格林函数来说是至关重要的.除了Farrell(1972)之外，Okubo和Endo(1985)、Guo等(2004)也对如何计算负荷勒夫数渐近值给出了不一样的理论计算方法.我们最近提出了计算位错勒夫数的渐近值的方法，在忽略自引力的情形下，渐近值可根据传播矩阵的特性很容易地求出(Zhou et al.，2021a).位错问题和负荷问题的差别在于边界条件的不同，因此该方法可直接应用于求取负荷勒夫数的渐近值.

本文首先对目前已有的上述三种计算渐近值的方法进行简单的回顾，然后着重介绍一种新的能够获取负荷勒夫数渐近值解析表达式的方法.最后将我们的方法与已有的计算方法进行了比较，并给出了定量的数值结果展示新的解析表达式在表达负荷勒夫数渐近特征方面的优势.

1 已有方法介绍

对于地球受力变形，我们采用如下的描述地球变形的微分方程组边值问题.其中，微分方程组为

(1)

其中λ，μ是拉梅常数，ρ是密度，g是重力加速度(习惯上称之为重力)，它们都是球坐标系的径向分量r的函数，G是万有引力常数，UL、UM、Φ、TL、TM分别是垂向位移、水平位移、附加引力位、垂向正应力、垂向剪应力的球谐展开的第n阶的系数(Pan et al.，2015)，Q满足

(2)

因此，这6个变量要分别对不同的球谐阶数n求解.该方程是研究地球在不同力源作用下发生静态变形的基础微分方程组，对于不同的力源需采用相应的边界条件(Love，1911；Farrell，1972；Okubo and Endo，1985；Sun and Okubo，1993).

对于地表质量负荷问题，通常将负荷看成点源，并且将该点源放置于北极点.由于对称性，在负荷作用下的变形与经度无关，即球谐展开的次数m=0，此时球函数退化为Legendre多项式.

下面介绍边界条件.为方便起见，我们定义两个矢量

(3)

在地心处正则，即

U(r=0)=0.

(4)

在内部边界连续，以及在地表

(5)

其中，ga是地表重力，a是地球半径.在推导该式中的边界值时，认为负荷点源的质量M满足单位引力位假定(即GM/a=1，可参考Sun and Sjöberg，1999)，也就是说负荷质量M=a/G=me/aga，其中me为地球质量.也有一些研究采用地球质量假定，即M=me(如Guo et al.，2004).不管用哪种定义，在计算格林函数时都要除以负荷质量以得到单位质量负荷的结果，因此只要推导过程自洽都不影响最终的结果.

负荷勒夫数定义为

(6)

其中，带下标n的负荷勒夫数hn、ln、kn表示对应于球谐展开的n阶的地表结果.因为(1)式是关于各个物理量的球谐展开系数的，所以不同的球谐阶数对应不同的勒夫数.相应的负荷格林函数为

(7)

其中，u，v和φ分别为垂直位移、切向位移和附加引力位，Pn是Legendre多项式，θ是计算点余纬.可以看到格林函数是一个无穷级数求和，需要截断处理.但是对于负荷问题需要截断到很高的阶数，这给计算带来很大的时间成本.为此Farrell(1972)根据Boussinesq问题的解(见下文)给出了负荷勒夫数的渐近值，从而可有效降低截断的阶数，并加速格林函数计算的收敛.

应用Kummer变换，(7)式改写为

(8)

其中，带下标∞的负荷勒夫数h∞、l∞、k∞表示相应的渐近值.由于负荷勒夫数渐近值具有严格解析表达式，右端的第二项通常具有用三角函数表示的严格解析形式(Farrell，1972；Zhou et al.，2019b)，而第一项求和的收敛要比(7)式中的求和快得多，因此截断阶数N可以取得足够小(对于位移与附加引力位，N=3000；对于倾斜或应变N=10000足以保证计算的收敛).可见负荷勒夫数渐近值在计算负荷格林函数时发挥着至关重要的作用.

对于当n很大时的情形，我们可以忽略液核的影响，因为液核的存在只影响较低阶的负荷勒夫数，所以可以采用纯固体的地球模型.实际上，正如下文将要讨论的那样，只有地球最外层的参数才会影响负荷勒夫数的渐近值，这也是为什么可以直接用均匀球(采用地球最外层结构参数和地表重力值，如Okubo，1988)或仅仅采用最外层参数(如郭俊义，2000；Guo et al.，2004)来解算负荷勒夫数的渐近值.

下面分别介绍目前已有的三种求解负荷勒夫数渐近值的方法.

1.1 Farrell方法

在球坐标系下，当角距离(θ)非常小的时候，问题就等效于平面的Boussinesq问题，因为此时地球的曲率效应可忽略(Farrell，1972).对于Boussinesq问题，采用柱坐标及柱函数(Bessel函数)系(用z，r，φ表示，将负荷点源放置于坐标原点，由于对称性，变形与φ无关.注意此时的r表示距离z轴的距离)，所有变量都利用Hankel变换(潘尔年等，1986)，即

(9)

其中，ξ表示波数.为了简便，仍用与球谐展开系数相同的符号表示变换后的系数.在此情形下，球函数趋近于柱函数，即

(10)

并且

(11)

因此，(7)式的求和可以表示成如下的积分：

(12)

根据(11)式，(12)式变成

(13)

对于Boussinesq问题，一个点负荷作用下的解为(在Hankel变换域)

(14)

其中ρa表示地球模型最上层的密度，即地表密度，〈ρ〉表示地球平均密度.将(14)式代入(9)式，并与(13)式进行比较，可得

(15)

在此过程中，要运用到(11)式中的n与ξ的近似关系n=aξ，因此其结果精度为O(1/n).我们称(15)式的结果为一级渐近值，以区别于Guo等(2004)给出的更高一级的渐近值.

1.2 Okubo和Endo方法

Okubo和Endo(1985)、Okubo(1988)推导负荷勒夫数渐近值的方法是基于Love(1911)给出的均匀球变形的通解表达式，用X=[ULUMΦTLTMQ]T表示由6个变量表示的这个通解矢量，其中上标T表示转置，其解可表示为

(16)

其中，c是由6个常数标量组成的待定系数矢量，且

[D(r)]=

(17)

(18)

(19)

式中

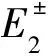
+[2f±+n(n+1)]zn(k±r)},

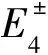
(20)

(21)

(22)

(23)

α和β分别为P波和S波速度，jn(x)是球Bessel函数，n为球谐阶数.利用边界条件(5)式可确定c，从而求得地表的位移与附加引力位，即

U(a)=D(a)[E(a)]-1T(a).

(24)

由于高阶负荷勒夫数只与最上层的结构有关，而如果采用密度为地表密度的均匀球，则该均匀球表面的重力将不等于真实地球的地表重力.Okubo(1988)指出，可用真实地球的地表重力值代替均匀球表面的重力，这样得到的负荷勒夫数渐近值就是真实地球的结果.因此地球模型的参数代入(24)式，并将各量展开成n的级数后，就可得到如(15)式所示的负荷勒夫数渐近值.

1.3 Guo方法

郭俊义等(郭俊义，2000；Guo et al.，2004)根据地表边界条件考察了每个变量与球谐阶数n的量级关系，得到

(25)

例如，TL随着n的增大而增大，与n呈线性关系，而UL不随n的增大而增大.然后通过变量代换

(26)

使得所有的新变量zi具有关于n相同的量级，并在微分方程中忽略高阶小量，从而得到

(27)

该微分方程组存在解析解，可以求出负荷勒夫数h和l的渐近值.但是k的渐近值无法求出，原因是舍去的项太多了.因此他们继续保留高一阶小量，并求解一个非齐次的微分方程组，从而求出了k的渐近值.

在此过程中，Guo等(2004)未介绍如何求得(27)式的解析解，而是直接给出了结果.因为该方程组实际上是变系数的，尽管将n/r移到了方程组的左边.所以其是否存在解析解，并不是那么直观地能够看出来.实际上，因为(27)式是欧拉型，所以通过变量代换，

r=eξ,

(28)

可将该方程组化成常系数的微分方程组，从而有解析解.Guo等(2004)以一级渐近值为基础，求解关于高一级小量的非齐次微分方程组，给出了更高一级的渐近值.但是对于负荷问题，更高一级的渐近值在计算负荷格林函数时是没有必要的，因为利用(15)式的渐近值已经能够很高效地获得收敛的格林函数(参考下文的图2).

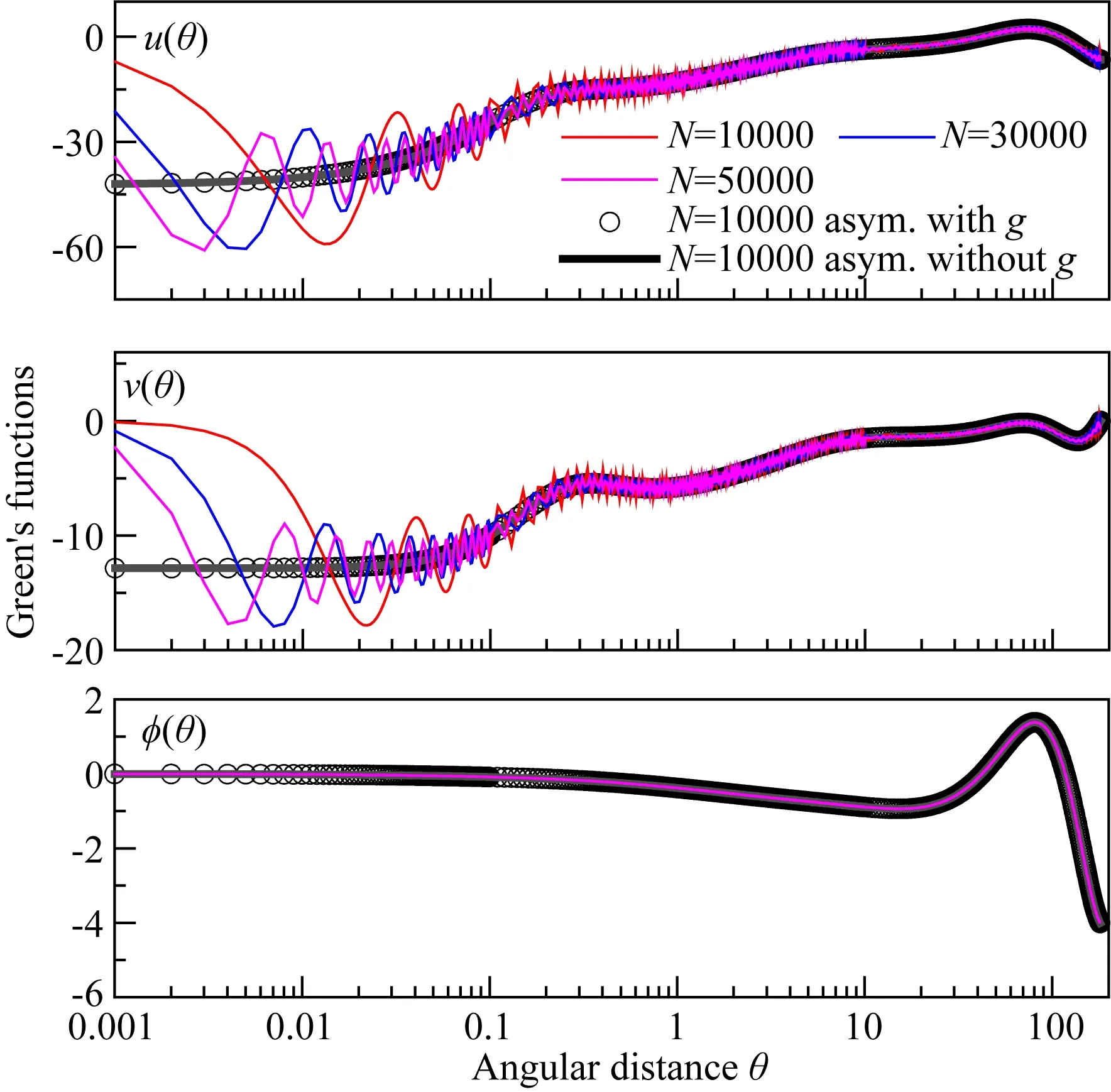
图2 负荷格林函数随角距离的变化(规格化系数为1012aθ)“asym.with g”表示采用考虑自引力的50000阶数值结果作为渐近值，“asym.without g”表示采用不考虑自引力的50000阶数值结果作为渐近值.

2 解析解方法

本文介绍的推导负荷勒夫数渐近值的新方法是以Pan等(2015)提出的解析法和DVP传播矩阵方法为基础.其中解析法的思想是使得地球变形的通解具有解析的形式，而DVP传播矩阵法是建立高阶地表负荷勒夫数与地表边界条件之间的直接联系.下面首先简单介绍解析法和DVP传播矩阵法，具体内容可参考(Pan et al.，2015)，然后给出推导负荷勒夫数渐近值的过程.

2.1 解析解构造

Pan等(2015)提出了求解(1)式的解析法.对于一个分层地球模型，(1)式是没有解析解的，但是通过合理的假设可以构造出近似的解析解.首先，在地核中假设每层密度是常数，重力是r的线性函数; 在地幔和地壳中，重力是常数，密度是r的反函数，如在第j层中，重力和密度满足

(29)

和

(30)

其中，b和c是常数，rj-1表示第j层的下边界，rj表示第j层的上边界，rc表示核幔边界的半径，ρ0j是第j层的平均密度，r0j是使该层质量守恒的等效半径，它满足

(31)

以上的假设是否合理，一方面可以考察假设后的模型与原模型的近似程度，另一方面取决于计算结果是否准确.Pan等(2015)的数值结果已经证明了结果的可靠性以及假设的合理性，实际上上述假设正是基于PREM模型的参数分布特征作出的，假设后的模型与原模型的符合程度是非常高的，差异仅为0.6%.并且这种方法也成功运用到求解位错以及地表热负荷引起的变形问题中，也被证明是非常高效的(Zhou et al.，2019a，b，2020，2021a,b).

此外，作一个变量代换

(32)

显然，对于j层的下边界有ξ=0.再以rTL，rTM和rQ为新变量，则(1)式变为

(33)

如果再假设第j层内的弹性模量为常数(目前的研究基本都是这么做的)，那么可以看出上述微分方程组的系数都是常数，这样就存在解析解.为简便计，把(33)式表示成矢量和矩阵的形式，即

(34)

其中，

(35)

为了方便，我们用球谐阶数n对变量作了规格化处理使各个变量量级相当.相应的矩阵A可从(33)式导出(系数作相应的调整，乘上与n有关的系数).此时，通解可以表示成(如在地球模型的第j层)

(36)

(36)式右边第一个矩阵是系数矩阵A的特征向量组成的矩阵，下标j表示它由第j层的参数计算获得，第二个矩阵中的s1和s2分别是由具有正实部(上标+)和负实部(上标-)的三个特征值组成，即

(37)

从而，由传播矩阵法建立第j层上下边界处(ξ=ξj和ξ=0)的两组解之间的关系：

(38)

其中上标u和l分别表示第j层的上下边界，上标-1表示矩阵求逆.然而，Pan等(2015)的数值结果表明，由于数值溢出，普通的传播矩阵方法，即(38)式，无法正确算出高阶(如n>6000)结果.下面要介绍的DVP传播矩阵法可以很好地解决这个问题.

2.2 DVP传播矩阵法

该方法的核心思想是避免导致溢出的大数产生，其技巧仅在于对普通的传播矩阵法进行小的改动，即

1)将(36)式改写为

由于ξj是常数，所以最终只是改变了待定系数，从(36)式中的c1变成(39)式的c3，并不会改变最终的解.

2)在第j层中，由上下边界的解我们可以得到与(38)式不一样的关系：

(40)

其中，

(41)

需要指出的是，这种传播矩阵方法的特别之处在于变量的位置关系与传统的传播矩阵方法是不一样的(对比(38)与(40)两式).从(41)式可以看出，在传播矩阵的计算中不涉及大的正数的指数，从而避免大数的产生，解决了溢出的问题.

2.3 渐近值推导

基于上面的方法原理，我们就可以推导出负荷勒夫数的渐近值.特别地，当球谐阶数n很大时，由于特征值接近于±n，所以(41)式中的〈-s1ξj〉和〈s2ξj〉都接近于0，当n为无穷大时，它们就等于0.因此(41)式变成

(42)

由(40)式进一步得到

(43)

这说明，当球谐阶数很大时，U和T是相关的，这种相关性会导致传统的龙格-库塔数值积分法无法准确计算出非常高阶的负荷勒夫数; 然而这种相关性可以使我们能够直接求得表面的负荷勒夫数渐近值.对于地球的最外层(设为第p层)，我们可由(43)式直接得出

(44)

其中，方括号的下标p表示方括号内的矩阵由第p层的参数求得.这说明，只要我们知道最外层的系数矩阵A的特征向量，就可以得到当n趋于无穷大时的U，从而得到负荷勒夫数的渐近值.

通常情况下，矩阵A的特征向量是无法解析地表达出来的.但是我们知道，对于地表质量负荷问题，在计算高阶的负荷勒夫数时，地球的自引力效应是可以忽略的，球谐阶数越高，自引力效应的影响越不明显(见下文图1).实际上Farrell(1972)从Boussinesq近似得到的渐近值也是忽略了自引力影响的.

图1 负荷勒夫数随球谐阶数的变化

对于忽略自引力的情形，在(33)式关于应力的微分方程中就可以舍去与密度或重力有关的项，从而位移和应力是与附加引力位无关的，因此可以首先解出(如Wason and Singh，1972；Fang et al.，2014)，然而附加引力位是与位移相关的，所以继续求附加引力位时需要求解一个非齐次的微分方程组，这也是1.3节中Guo等(2004)求负荷勒夫数k的渐近值采用的方法，但这反而增加了难度.实际上，我们可以直接运用2.1节的方法，此时矩阵A的特征向量可以很容易地求出(如通过MATLAB的符号运算，具体表达式可参考Zhou et al.，2021a).

因此根据矩阵A的特征向量，以及(5)式和(44)式可以很容易求得

(45)

(45)式是高阶负荷勒夫数的严格解析表达式，给出了负荷勒夫数与球谐阶数n的关系.特别地，当n趋于无穷大时, 取极限就得到

(46)

由于我们是求负荷勒夫数在n趋于无穷大时的渐近值，我们可以将第p层设得足够薄，因此有

ρ0pr0p=ρaa,

(47)

即地表密度与地球半径的乘积.这样就可以得到与(15)式完全一致的结果.实际上对于最外层来说，地球模型通常是均匀的，因此ρ0p就是这个平均值，而由(31)式计算得到的r0p实际已经非常接近地球半径a了(对于PREM模型来说，误差小于万分之三)，就算直接使用r0p也可以确保k∞的准确性.

2.4 数值结果

图1给出了根据(45)式确定的负荷勒夫数随球谐阶数的变化, 并与Guo等(2004)考虑高一阶小量的渐近值进行了比较.其中地球模型采用PREM(Dziewonski and Anderson, 1981)，其最外层的海洋层替换为固体层，其参数设置如下：λ=3.43×1010Pa，μ=2.66×1010Pa，ρ=2600 kg·m-3.从图中可以看出，随着球谐阶数n的增大，负荷勒夫数趋近于一个常数.由于我们推导高阶负荷勒夫数解析公式时未考虑自引力的影响，因此所得结果在高阶部分与不考虑自引力的数值结果比较接近，在n=5000左右时二者就已经比较一致；但是在低阶部分与考虑自引力的数值结果仍然存在很大的差异.通常计算负荷格林函数时只要考虑10000阶以下的负荷勒夫数，因此在研究负荷形变时自引力的影响一般是需要加以考虑的.但是从图中可以看出，随着n的增大，自引力的影响越来越小，因此在研究负荷勒夫数渐近特征时，自引力是可以忽略的，这可从图1中不同结果在n很大时具有的一致性得到验证.

此外，我们也将本文给出的渐近值与Guo等(2004)的结果进行了比较.结果说明，在n<20000左右时，Guo等(2004)的渐近值与考虑自引力的数值结果更加接近，这是因为他们推导渐近值时部分地考虑了自引力的影响；但是对于n>20000的部分，我们的结果不管是和考虑自引力还是和不考虑自引力的数值结果都更加接近，对于位移的勒夫数，这种情况更加明显.

为了显示渐近值在计算格林函数中的作用，作为例子，我们根据(8)式计算了垂直位移、水平位移和附加引力位的格林函数随角距离θ的变化关系，结果如图2所示.为了更好的显示结果，格林函数值都乘上了一个规格化系数1012aθ.首先，通过对比采用不同渐近值获得的格林函数，发现渐近值之间的微小差异不会影响格林函数的计算.并且我们发现负荷勒夫数渐近值在附加引力位的计算中并不是必需的，不采用Kummer变换同样可以获得收敛的格林函数.图2也说明了如果不采用Kummer变换，即使截断阶数N=50000，位移格林函数仍然是不收敛的，说明渐近值对于位移格林函数的计算来说是必不可少的，这从另一个侧面证明了渐近值的重要性.

3 讨论

从2.3节的推导我们可以看出，负荷勒夫数的渐近值只和地球模型地表的参数有关，而不论地球内部的结构如何.其实，这一点早就为我们所熟知，即高阶的负荷勒夫数与地壳和上地幔介质密切相关，因此采用龙格-库塔方法计算高阶负荷勒夫数时可以直接从地幔开始积分.然而，通过我们的推导可以从本质上了解其原因：地球每个分层内的U和T之间的相关性随着球谐阶数的增大而增加，从而地表的负荷勒夫数可由地表的边界条件直接确定.

相比于Okubo和Endo方法，我们给出的新方法不需要作均匀球的假设(或基于均匀球模型开展相关推导)，不需要用真实地球的地表重力代替均匀球表面的重力.目前基于均匀球的地球受力变形的数值模拟必须要替换地表重力才能得到正确的结果，如Sun(2004)对位错引起的地表位移场变化的模拟.与Guo等(2004)的方法一样，我们的方法实际上也只需要考虑地球模型的最外层即可.

从Guo等(2004)给出的负荷勒夫数渐近值的更高阶的结果可以看出，在位移(h和l)结果中耦合进了重力的影响.但是将(44)式展开成n的罗朗级数后高阶解中没有重力项，原因在于我们忽略了自引力的影响.对于地表负荷问题，忽略自引力不会影响负荷勒夫数渐近值的一级结果，即O(1)量级的常数项，但是会影响高一级的结果，但是这种影响随着球谐阶数的增大越来越弱，并且高一级的结果在格林函数的计算中是不必要的.在2.3节中我们忽略自引力的目的是为了获得矩阵A的特征向量的解析形式，从而获得渐近值的解析形式，这样就可以运用Kummer变换.Kummer变换的关键有两点：一方面，渐近值必须与实际的勒夫数比较接近，从而它们的差是一个高阶小量，并且这个差异随着球谐阶数的增大而减小，这样(8)式右端的第一个级数求和能够很快地收敛；另一方面，渐近值需要具有严格解析式，从而(8)式右端的第二个级数求和有简单的解析式，能够用简单的函数表示.Chen等(2018)采用的刚度矩阵法或者2.2节介绍的DVP都能够计算任意球谐阶数的负荷勒夫数，但是要获得收敛的负荷格林函数，具有解析表达式的渐近值对于简化负荷格林函数的计算仍是非常必要的，因为截断到很高的球谐阶数是很费时低效的.采用拟合的方法确定当n非常大时的勒夫数随n变化的解析式(即渐近值)也是一个非常有效的方法(如Pan et al.，2015；Zhou et al.，2019b).

本文的方法除了采用Pan等(2015)的解析解方法获得常微分方程组的系数矩阵A的特征向量解析表达式外，另一个关键之处是采用了DVP传播矩阵方法，(42)式显示了其独特的性质，阶数n越大，其计算方面的优越性越明显.DVP方法只是在传统的传播矩阵方法基础上作了小的改动，变换了变量的位置，就解决了数值溢出的问题，并且计算也非常的高效.

最后需要强调的是，从表面上看，本文的方法涉及构造解析解的理论方法和DVP传播矩阵方法.实际上推导负荷勒夫数的过程非常简单，可以分成以下两个步骤：首先计算常微分方程组的系数矩阵A的特征向量从而得到(44)式右端方括号中的矩阵；然后根据地表边界条件由(44)式通过矩阵运算直接得到需要的渐近值的解析表达式.该过程只涉及矩阵特征向量的计算及相关的矩阵运算，原理简单，也非常容易编程实现(Pan，2019；Zhou et al.，2019a).

4 结论

本文基于求解地球变形的解析解方法和DVP传播矩阵方法，导出了高阶负荷勒夫数的解析表达式，进而确定了负荷勒夫数的渐近值.渐近值的推导只与地球模型的最外层有关，推导过程只涉及矩阵特征向量计算和简单的矩阵运算.本文所得结果与已有方法给出的结果是一致的，并且更加准确地描述了负荷勒夫数的渐近特征.

利用DVP传播矩阵法对于n非常大时所具备的特点，我们不但可以看出变量U和T的关联性，这也是导致传统的龙格-库塔数值积分法失效的本质原因，还可以直接根据地表边界条件求出负荷勒夫数的渐近值.这说明DVP传播矩阵法在数值计算方面有其独特的优势，可以广泛应用于分层地球模型的变形研究中，如负荷形变、地震形变等静态变形问题，以及地球简正模或合成地震图等动态变形问题中.

致谢本文第二作者于1982年至1984年在北京大学地质系师承王仁教授攻读硕士学位，学位论文题目为《成层地球模型对体势力及表载的响应》.该论文利用球谐函数与传播矩阵方法研究分层球形地球在日月引潮力和地表负载作用下的位移场和应力场变化，并采用数值积分方法计算勒夫数.在王仁教授的教诲下，科研能力得到了很大的提升，为后来从事力学和数学相关的研究奠定了坚实的基础，对现在的研究工作仍有很大的帮助.