动态价格下含时滞的Logistic渔业模型的Hopf分支

张 桓，张 悦

(东北大学 理学院， 沈阳 110819)

随着人类对海洋渔业的生物资源需求的增加，合理的捕捞及有效利用市场资源越发重要。海洋管理需要实现可持续开发一直是生物学家与经济学家关注的热点问题[1-2]。考虑一个标准的渔业开放模型[3]，研究文献经常将价格考虑为不变量。1954年Gordon[4]把价格成本引进生物经济模型，假设单位价格和捕获成本为常数，而渔业的价格和市场结构变化迅速，市场价格受渔业供给关系影响。针对管理市场价格相互作用的需要，建立了渔业经济模型[5]，因此，在模型的基础上添加了市场上资源价格的动态变化。根据文献[6]，价格的变化取决于需求函数(鱼类的销售量)和供给函数(渔获量)之间的关系。文中假设价格变化快于鱼类库存量的变化，因此通过一个小的正参数s来调整价格动态，称为价格动态变化速度[7]。该参数反映了市场价格的弹性变化。

不仅如此，在渔业模型中，时滞现象的考虑也成为新的突破点。描述不同生态相互作用的时滞总是不同的，因此分别讨论每种时滞对鱼类种群和市场价格的动力学的影响有助于确立合适的管理措施。Celik[8]研究了一类种群具有时滞的模型，以时滞τ为参数，分析了模型唯一正平衡点的局部渐近稳定性与Hopf分支的存在性。鱼类种群与市场价格的动态发展趋势不仅依赖于当前的状态，还依赖于过去或未来某一时间段的状态影响。引入时滞会影响系统的稳定性并产生分支，而系统中分支的出现将使渔业的变化规律更加的复杂。叶志勇等[9-10]探讨了经典生物模型的稳定性与Hopf分支。刘聪颖等[11-12]根据对两类具有时滞的种群动力学模型的定性分析，结合稳定性理论讨论了正平衡点的全局渐近稳定的充分条件。秦丽等[13-14]讨论了双时滞在阶段结构的模型中平衡点的局部渐近稳定性及Hopf分支。因此，本文选用具有时滞的微分方程分析动态模型。俞美华[15]研究了价格变化的生物种群经济捕获模型，并在此基础上建立具有时滞的经济捕获模型，采用时滞方程的稳定性理论对正平衡点稳定性进行分析，从而得出时滞会改变平衡点稳定性的结论。

本文从新型动态价格下种群的Logistic生长模型出发，根据具有双时滞和价格的复杂性的生物经济模型，通过改变时滞和复杂性参数来检验局部稳定性和存在性。研究了Hopf分支方向和分支的稳定性，分析了生物捕捞业复杂性和多时间延迟对生物经济捕食者-种群模型动力学的影响。

1 模型的建立

考虑一个有关渔业在动态价格下[16]具有双时滞的Logistic模型，系统描述如下：

(1)

式中：x(t)是在t时刻的鱼群储存量(t)，x(0)=x0>0；p(t)是储存量在t时刻的单价(万元/t)，p(0)=p0>0；a-p(t)为正线性需求函数[17]；Y是常数捕获率(t/天)；r为鱼群每日的内禀增长率；τ1、τ2分别表示鱼群和市场价格的时间延迟；k为环境承载能力(t)；s为价格动态变化速度；a为正常数参数，表示市场容量。

2 局部稳定性与Hopf分支

以下讨论正平衡点E的局部渐近稳定性与在平衡点E处Hopf分支的存在性。

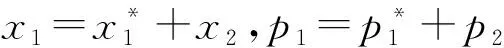
(2)

其雅克比矩阵为：

系统(2)对应的特征方程：

(3)

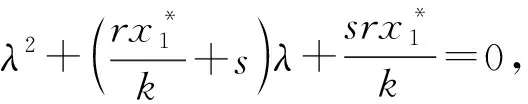
现在讨论以下5种情况下，2个时滞对正平衡点E稳定性的影响。

1) 只有鱼类种群受时滞影响，即τ1>0，τ2=0。

在此情况下，特征方程(3)可简化为：

λ2+(Ae-λτ1+s)λ+sAe-λτ1=0

(4)

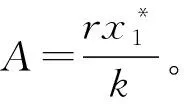
假设λ=iω1为方程的一个根，将iω1(ω>0)代入方程(4)中，则有

(5)

分离上述方程的虚部与实部，得：

(6)

把上述方程的两端平方相加，得到关于ω1的方程：

(7)

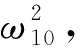
(k=0，1，2，…)，对应的τ1k>0使得方程(4)有一对纯虚根±iω10。

运用Butler引理[18]，可以得出在s2+A2<6s2A2条件下，当τ1<τ10时，模型(2)的内部平衡点是局部渐近稳定的。

接下来，对方程(4)求关于τ1的导数：

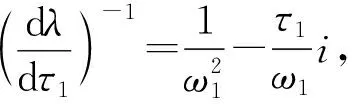
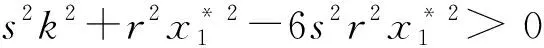
当|τ1-τ10|<<1时，发生Hopf分叉。也就是说，模型(2)有一个周期解分支，该分支来自正平衡点E在τ1=τ10附近的分支。

当τ1>τ10时，模型(2)的正平衡点E是不稳定的。

2) 只有市场价格受时滞影响，即τ1=0，τ2>0。

类似于1)的分析过程，有下述结果：

当s2+A2>6s2A2时，特征方程存在唯一正实根ω20。 其对应的时滞为：

(k=0，1，2，…)

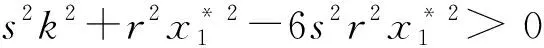
当τ2>τ20时，模型(2)的正平衡点E是不稳定的。

3) 当鱼类种群与市场价格均受时滞影响，τ1为参数，即τ1>0，τ2∈[0，τ20)，并且τ1≠τ2。

在此情况下，特征方程为:

λ2+(Ae-λτ1+se-λτ2)λ+

sAe-λ(τ1+τ2)=0

(8)

设λ=iω11(ω11>0)为方程的一个根，将iω11代入方程(5)中，则：

sAe-iω11(τ1+τ2)=0

(9)

分离上述方程的虚部与实部，并将所得方程两边平方相加，得到关于ω11的方程：

2sA2ω11sinω11τ2+s2A2=0

(10)

当满足s2+A2>6s2A2时，关于上述方程存在唯一正实根ω11。

(m=0，1，2，…)

对应的τ1m>0使得方程(8)有一对纯虚根±iω11。

运用Butler引理[18]可以得出：在s2+A2<6s2A2条件下，当τ1>0，τ2∈[0，τ20)时，模型(2)的内部平衡点是渐近稳定的。

对方程(8)求关于τ1的导数，并计算：

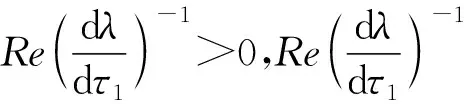
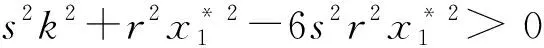
当τ1∈[0，τ10)，τ2∈[0，τ20)时，

模型(2)的正平衡点E是局部渐近稳定的；

当τ1=τ10时，发生Hopf分叉。也就是说，模型(2)有一个周期解分支，该分支来自于正平衡点E在τ1=τ10附近的分支。

当τ2∈[0，τ20)，τ1>τ10时，模型(2)的正平衡点E是不稳定的。

4) 当鱼类种群与市场价格均受时滞影响，τ2为参数，即τ1∈[0，τ10)，τ2>0，并且τ1≠τ2。

类似于2.3的分析过程，有下述结果：

当满足s2+A2>6s2A2时，关于方程：

2s2Aω22sinω22τ1-s2A2=0

(11)

存在正实根ω22，其对应的时滞为：

(n=0，1，2，…)

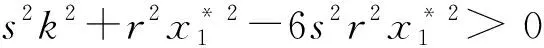
当τ1∈[0，τ10)，τ2∈[0，τ20)时，

模型(2)的正平衡点E是局部渐近稳定的；

当τ2=τ20时，发生Hopf分叉。也就是说，模型(2)有一个周期解分支，该分支来自于正平衡点E在τ2=τ20附近的分支。

当τ1∈[0，τ10)，τ2>τ20时，模型(2)的正平衡点E是不稳定的。

5) 当鱼类种群与市场价格均受相同时滞影响，即τ1=τ2=τ(τ>0)

此时，特征方程变成：

λ2+(A+s)λe-λτ+sAe-2λτ=0

(12)

在方程(12)两边同时乘以eλτ，可得:

λ2eλτ+(A+s)λ+sAe-λτ=0

(13)

假定λ=iω(ω>0)是(13)的根，则有：

-ω2eiωτ+(A+s)iω+sAeiωτ=0

(14)

分离上述方程的虚部与实部：

(15)

将上述方程两边平方相加，得到关于ω的方程：

ω4+s2A2-2ω2sA(cos2ωτ-sin2ωτ)-

(A+s)2ω2=0

(16)

当满足s2+A2-4s2A2+2As>0时，关于上述方程存在唯一正实根ω0。

(j=0，1，2，…)

对应的τj>0使得方程(12)有一对纯虚根±iω0。

在s2+A2-4s2A2+2As<0条件下，当τ<τ0=min{τj}时，模型(2)的内部平衡点是渐近稳定的。

假设λ(τ)=x(τ)+iω(τ)是方程(12)在τ=τ0处的根。则方程(12)关于τ的导数为：

从而得到横截性条件：

定理5对于模型(2)，若s2+A2-4s2A2+2As<0成立，则：当τ<τ0，

模型(2)的正平衡点E是局部渐近稳定的；

当τ=τ0时，发生Hopf分叉。也就是说，模型(2)有一个周期解分支，该分支来自正平衡点E在τ=τ0附近的分支。

当τ>τ0时，模型(2)的正平衡点E是不稳定的。

3 数值模拟算例

令模型(2)中，r=0.015，k=1 802.6，Y=7，a=800，s=0.005，则模型(2)存在平衡点E1，这些系数满足上述条件，当不考虑时滞时，正平衡点E1渐近稳定，如图1所示。

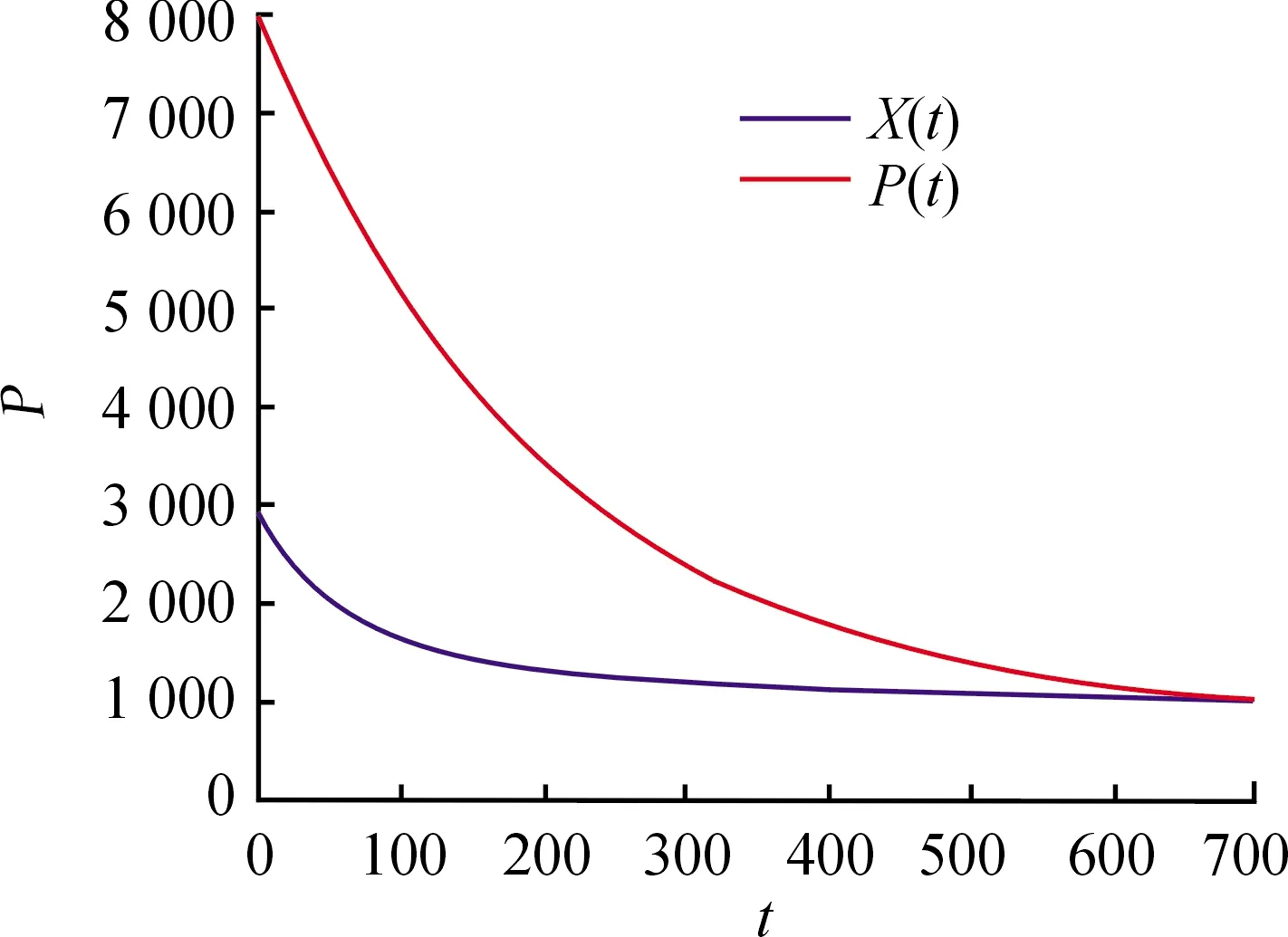
图1 当τ1=τ2=0时，平衡点E1渐近稳定曲线

令模型(2)中，r=0.015，k=1 703.2，Y=7，a=800，s=0.071，则模型(2)存在平衡点E1。当只有市场价格受时滞影响时，τ1=0，基于第2部分的分析，当这些系数满足上述条件，根据计算可得ω20，τ20。图2表明：当τ1=0，τ2=10.35时，平衡点E1渐近稳定；当τ1=0，τ2穿过τ20时一个稳定的周期解从平衡点E1分支出来。

图2 当τ1=0，τ2=10.35时，系统出现渐近稳定曲线；当τ1=0，τ2=22.12时，系统出现稳定的周期解曲线

令模型(2)中，r=0.015，k=1 802.6，Y=7，a=800，s=0.989，则模型(2)存在平衡点E1。当只有鱼类种群受时滞影响时，τ2=0，基于第2部分的分析，当系数满足上述条件，根据计算可得ω10，τ10。图3表明：当τ1=39，τ2=0时，平衡点E1渐近稳定；当τ2=0，τ1穿过τ10时一个稳定的周期解从平衡点E1分支出来。

图3 当τ1=39，τ2=0时，系统出现渐近稳定曲线；当τ1=45.3，τ2=0时，系统出现稳定的周期解曲线

令模型(2)中，r=0.015，k=1 602.6，Y=7，a=800，s=0.076，则模型(2)存在平衡点E1，对固定的时间延迟τ1=2，当系数满足上述条件，可计算得出ω22，τ20。图4表明：当τ1=2，τ2=16时，平衡点E1渐近稳定；当τ1=2，τ2穿过τ20时一个稳定的周期解从平衡点E1分支出来。

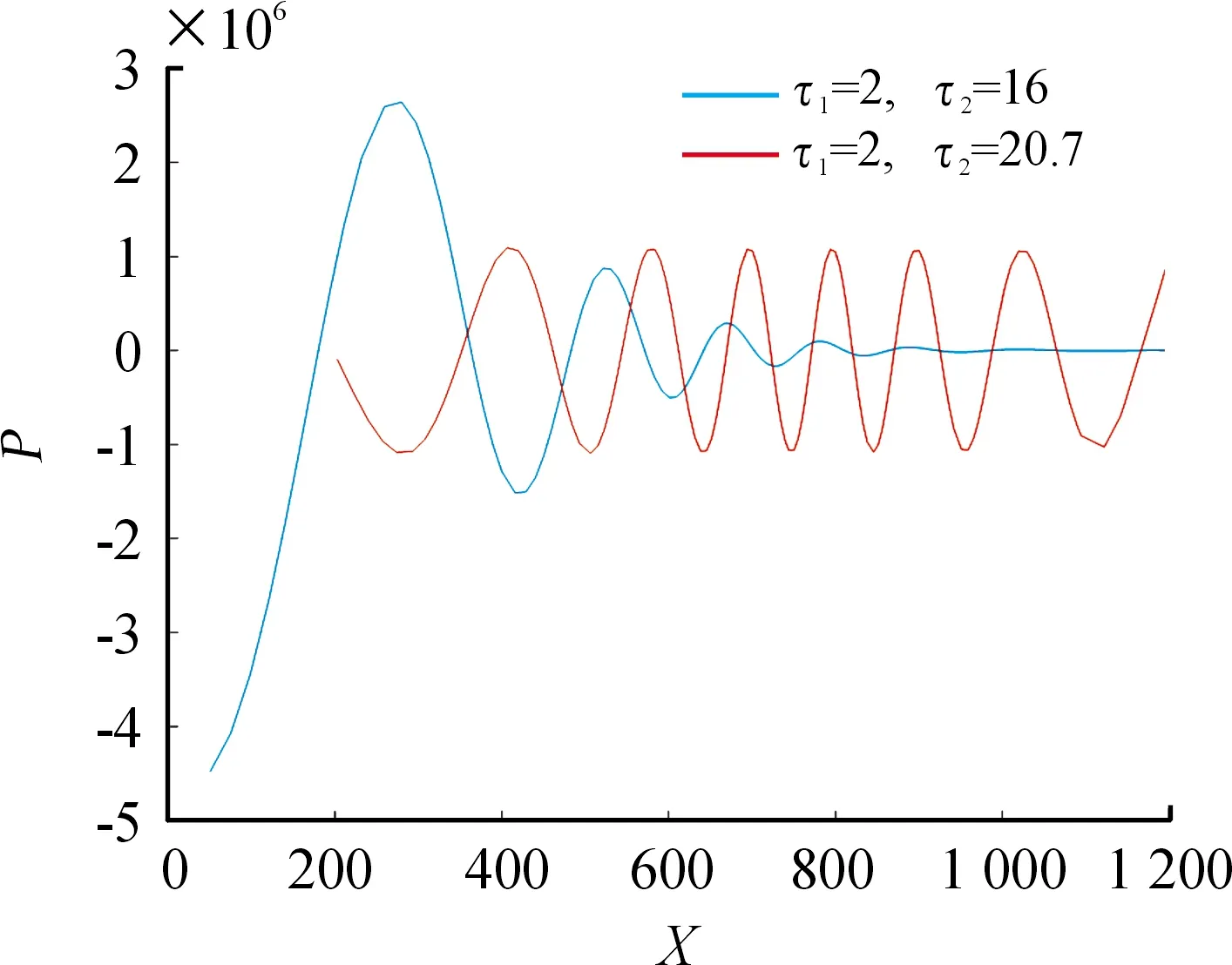
图4 当τ1=2，τ2=16时，系统出现渐近稳定曲线；当τ1=2，τ2=20.7时，系统出现稳定的周期解曲线

4 结论

1) 研究分析，当模型(2)存在正平衡点时，在不考虑时滞即τ1=τ2=0的情况下，此时正平衡点渐近稳定。双时滞在5种不同情况下会影响模型正平衡点的稳定性。

2) 当只有市场价格(或只有鱼类种群受时滞影响)时，若上述条件成立，则当时滞满足τ1=0，τ2∈[0，τ20)(或τ1∈[0，τ10)，τ2=0)时，渔业模型(2)的正平衡点E是局部渐近稳定的，当τ2=τ20(或τ1=τ10)时，发生Hopf分叉，此时稳定的周期解出现。

3) 当鱼类种群与市场价格均受时滞影响，τ1为参数，若上述条件成立，则当时滞τ1>0，τ2∈[0，τ20)时，渔业模型(2)的正平衡点E是局部渐近稳定的，意味着此时渔业种群与市场价格都趋于稳定状态；当τ1=τ10时，发生Hopf分叉。也就是说，模型(2)有一个周期解分支，该分支来自于正平衡点E在τ1=τ10附近的分支。

4) 而当渔业种群与市场价格均受相同时滞影响，即τ1=τ2=τ，当满足相应条件时，模型(2)的内部平衡点是渐近稳定的。说明当时滞达到某个临界值时，会影响种群与市场价格平衡的稳定性并导致Hopf分支的出现。

5) 通过时滞的影响，渔业活动的稳定性和市场价格进一步得到了保证，在适当的时候对于最优捕鱼期和生物休渔期的制定管理措施有一定的帮助。本模型的一个重要局限性是没有考虑环境影响的随机性，接下来将在模型的基础上引入随机变量研究系统的稳定性。