基于改进GMRES 算法的水冷壁运动机器人路径跟踪模型预测控制①

黄 巍 占红武 胥 芳

(浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点实验室 杭州310023)

0 引言

近年来,非完整轮式移动机器人[1](non-holonomic wheeled mobile robot,NWMR)在运输、探测、救援等领域引起了广泛的关注。如在火电厂中,其应用范围覆盖了水冷壁面巡查检测、缺陷定位[2]和主辅机关键部件裂化评估维护[3]。人们对NWMR的运动控制[4]进行了更加深入的研究,提出了各种控制方法,其中包括神经网络控制法[5-6]、滑膜控制[7]和非连续反馈控制法[8]。但当考虑控制输入以及约束处理时,以上算法很难达到较为直观的效果。然而,非线性模型预测控制法(nonlinear model predictive controller,NMPC)却可以很好地解决这个问题,该控制方法以当前时间间隔下NWMR 状态的预测量为初始条件,基于反馈控制律对系统的未来轨迹进行预测,利用控制序列对性能指标函数进行优化。在此框架下构造的最优化问题具有高度的灵活性[9]、良好的动态性及鲁棒性,因此在处理多变量多约束问题时表现优秀,吸引了大量研究者的目光。文献[10]设计了一种非线性模型预测控制算法(NMPC)用于解决误差动力学的轨迹跟踪控制问题。文献[11]针对自主水面舰艇的非线性MPC 轨迹跟踪控制问题,为提高算法效率引入了启发式方法来处理输入约束。文献[12]针对NMPC 求解优化问题的滚动可行性问题,将参考轨迹作为性能指标的终端约束以此保证算法收敛。

然而,NMPC 所带来的高计算负荷不可避免地与较小的采样周期产生冲突。为了提高运算速度,满足实时性要求,许多研究者都致力设计有效的在线算法,诸如快速梯度下降[13]、计算除法[14]、延迟补偿[15]及数值连续法[16]。作为结合连续法[17]和Krylov 子空间法[18]的算法,连续/广义极小残余算法[19](continuation/general minimum residual,C/GMRES)已经发展成为一种求解NMPC 的快速算法。该算法通过确定控制序列在每个时间间隔的增量,而非迭代求解,提高了运算速率。

本文研究了水冷壁爬壁机器人(water wall climbing robot,WWCR)的非线性模型预测控制(NMPC)路径跟踪问题。利用WWCR 实时状态与虚拟目标状态之间的误差为模型,建立路径跟踪问题NMPC 框架,基于庞特里亚金极小值原理,转换为Bolza 形式的NMPC 最优控制问题。鉴于文献[20]的C/GMRES 算法同时具备数值连续法与Krylov 子空间方法的优点,引入该算法对NMPC 进行计算求解。然而其算法未能完全考虑NWMR 路径跟踪问题中状态与输入向量不等式约束,本文通过引入正则平滑函数(Fischer-Burmeister,FB),将不等式约束与其互补条件联立构建最优化条件方程,引入多重打靶法,将误差分布到状态向量与共态向量之中,以此提升算法的控制精度。在求解过程中,对约束和控制输入向量进行延拓,提出一种压缩变量的优化方法,对方程进行简化处理,减小线性方程大小,同时对C/GMRES 算法中的残量求取进行优化,避免Hessenberg 矩阵的分解运算,降低了算法的计算负载,加快算法运行速度。最后进行仿真,验证该算法的可行性。

1 非线性模型

本文实验对象主要针对履带式爬壁机器人(NWMR),定义图1 所示的世界坐标系{q},建立路径跟踪模型,工作环境如图2 所示。

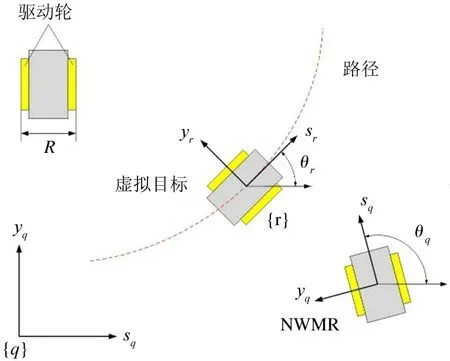
图1 路径跟踪模型

图2 水冷管壁图

定义NWMR 所处位置为(sq,yq),其速度为v,角速度为ω。

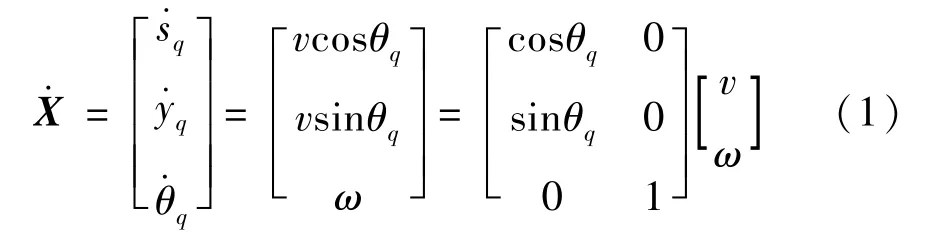
其中X=[sq yq θq]T为状态向量,U=[v ω]T为控制输入向量。

定义虚拟目标所处坐标系为{r},需要跟踪的路径为[sr yr θr]T。Ur=[vr ωr]表示参考控制信号矢量。考虑到在实际跟踪时由于外部因素导致的局部跟踪误差,定义误差状态由Xe=[se ye θe]T表示,由此可得NWMR 的动态误差模型:

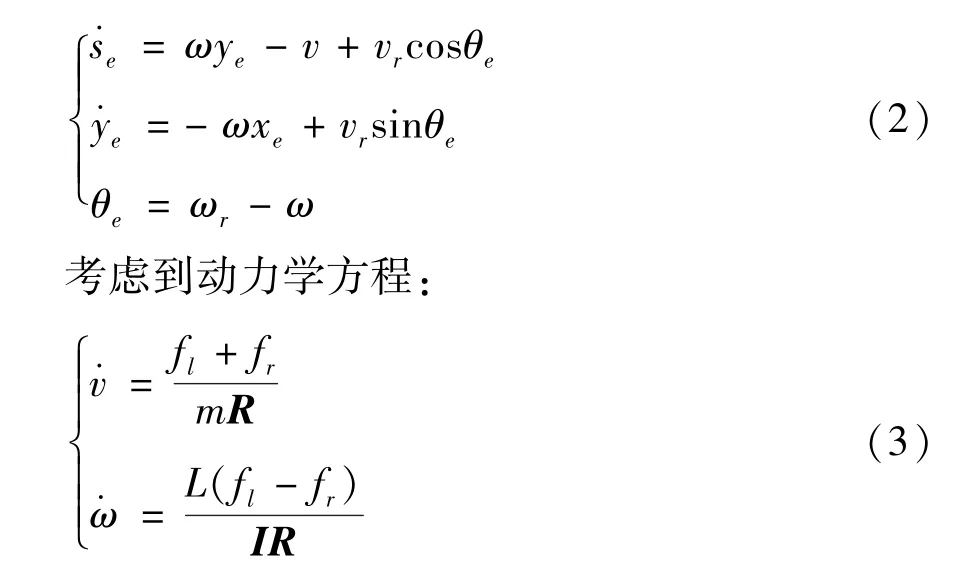
其中,fl与fr分别表示左右履带电机的输入驱动转矩,m与I分别为NWMR 的质量及其惯性矩。在实际工作中,考虑到由于外部因素导致速度突变引起的运行不稳定,利用虚拟控制量表示NWMR 的加速度与角加速度,对动力学系统简化为

根据式(2)～式(4)扩展系统状态,可得闭环系统状态方程为

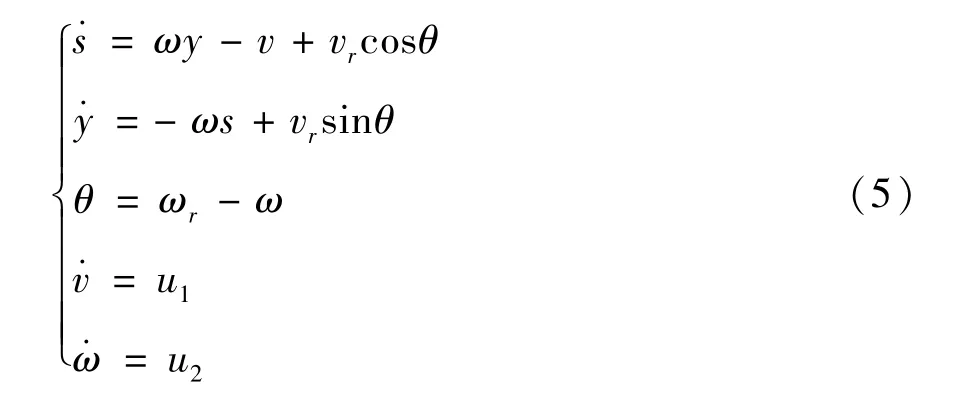
令x=[s,y,θ,v,ω]T为NWMR 的状态向量,控制输入向量为u=[u1,u2]T。

则式(5)中的闭环系统可用如下非线性表达式表示。

根据上述建立的模型,便可将路径跟踪问题转换为寻根问题,即通过寻找相对最优的虚拟输入u合适的控制率,满足Xe=0。

2 快速非线性模型预测控制方法

基于目标函数的内点[21](inner point,IP)重新构造的转换方法,将潜在的优化问题转化为等式约束进行求解,是处理NMPC 的常用方法之一。虽然在一定程度上导致了两点边值问题(twopoint boundary value problem,TP-BVP),但是这种基于PMP 的间接法仍然是求解OCP 问题较为有效且精度较高的方法。作为一种非线性滚动时域控制的快速数值算法,GMRES 算法避免了传统的牛顿型数值算法中复杂的Riccati 微分方程,其基于序列公式,在每个采样时间仅进行一次求解,同时利用前向差分替代部分方程近似值,以此来提高运算速度。针对算法内部的标准基构造进行改进,加快了计算速度。对于约束问题,引入Fischer-Burmeister 正则化平滑算法(FBRS)[22],利用FB 函数将最优性的必要条件映射到非光滑方程组,以增加算法的稳定性。融合多重打靶法来提高计算精度,并对残量求取进行优化处理。

2.1 问题描述

针对模型建立的NMPC 问题,在不失一般性的情况下,可将其描述为Bolza 形式的最优控制问题,同时考虑在预测范围内的阶段目标函数L以及出现在范围末端的终端目标函数V。

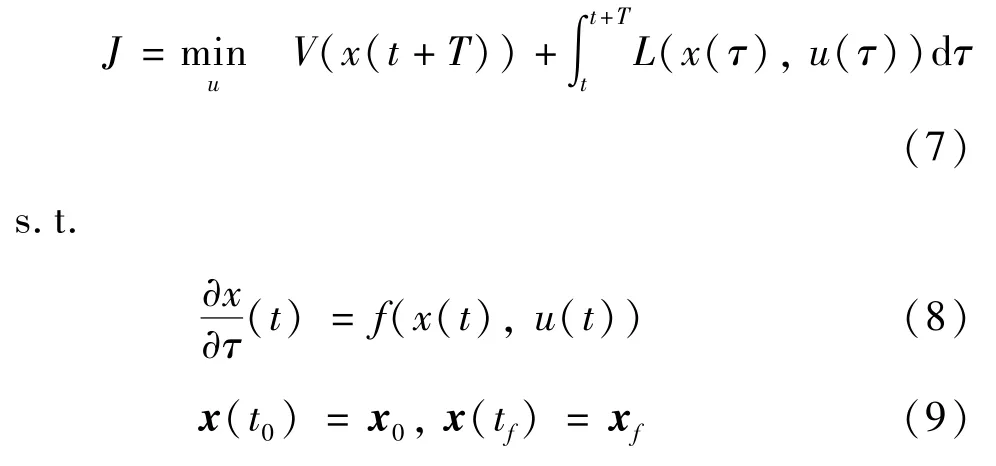
其中,式(9) 作为边界条件,x0和xf分别表示NMWR 的初始状态和终止状态。式(10)表示约束,考虑虚拟输入向量u的引入,定义非线性系统的不等式约束g(x,u) 如下所示。

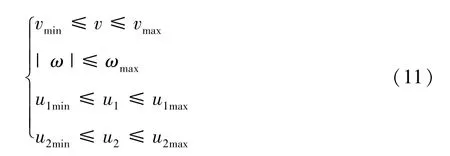
式(7)中,V(x(t+T)) 表示终端约束,表达式为

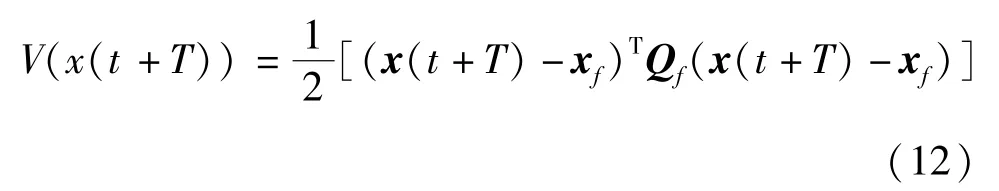
其中,Qf为终端状态权重矩阵。右侧第2 项为拉格朗日被积函数,表达式为

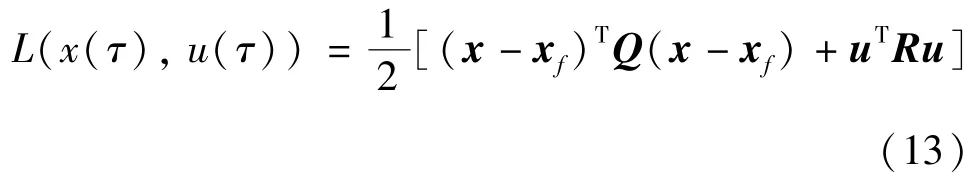
上式中Q=diag{q1,…,q5}、R=diag{r1,r2} 均表示权重矩阵,qi、ri为非负常数。在上述性能指标函数中,第1 项表示NWMR 系统模型,第2 项为其边界条件。

2.2 不等式约束

针对不等式约束,对计算求解带来很大的负担,许多文献通过各种办法将不等式转变为等式约束来计算,例如引入外部障碍函数[23]、势垒函数[24]、辅助变量法[25]。本文通过引入FBRS,同时使用来自对偶空间的信息生成不同的搜索方向,即算法同时在原始空间和对偶空间中运行找到原始OCP 及其对偶的解。使用非线性互补(NCP)函数将互补条件式(10)映射到方程组。定义广义半光滑函数为

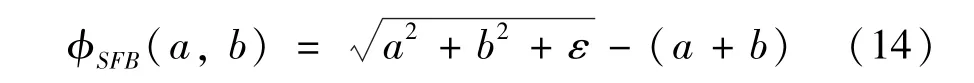
其中ε >0,为正则参数。将拉格朗日算子μ及不等式约束g(x,u) 作为互补条件代入半光滑函数,得到:

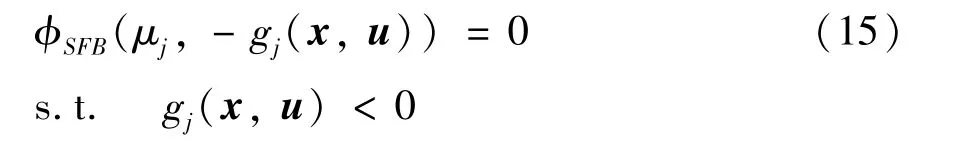
需要注意的是附加的拉格朗日乘子μ必须加入到输入变量Ut中迭代计算,记为

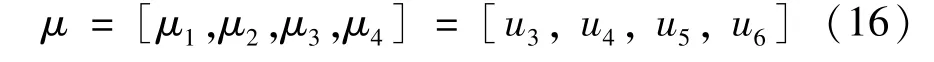
为避免当虚拟输入变量为0 时导致的C/GMRES优化更新时的奇异性,需要在代价函数中引入惩罚因子,则拉格朗日函数修改为

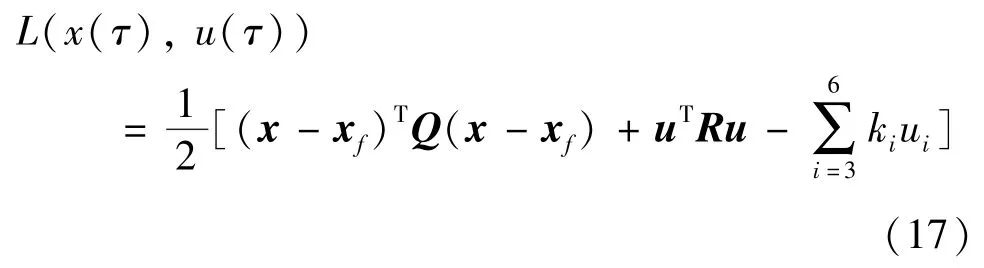
为避免惩罚因子过大而对寻找最优解产生影响,故选择ki为小的正常数。

2.3 最优化条件

通过Karush-Kuhn-Tucker (KKT)最优性条件导出求解动态OCP 的最优性条件,利用广义哈密顿函数表示:

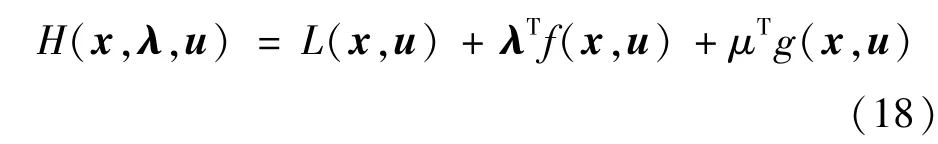
其中,λ表示共态向量。为了解决TP-BVP 中,控制输入函数为未知量的情况,将预测范围T分为N个阶段,达到利用有限个参数来表示控制输入函数的目的。使用欧拉-拉格朗日方程变分法来离散化求解动态OCP 最优化的必要条件。离散化如下:

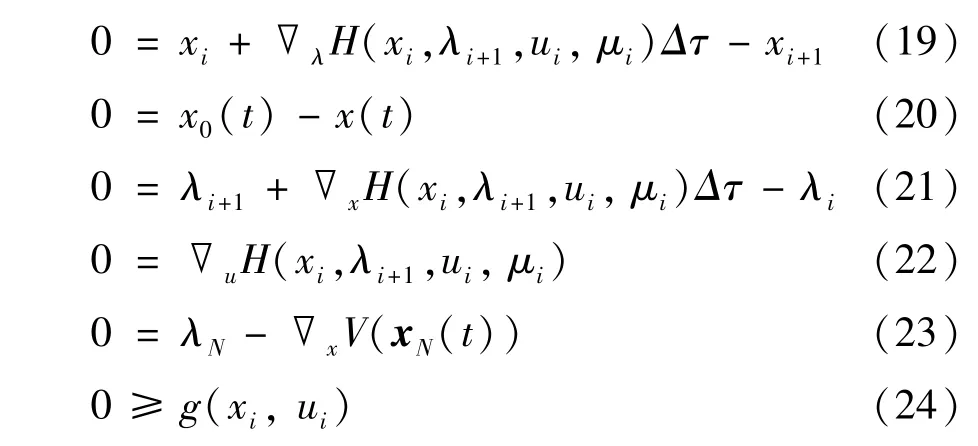
其中Δτ=T/N。分别用和表示在离散视界上的状态序列、共态序列以及控制输入序列。通过以上离散化的方法,成功地将NMPC 表示为时间t时测量状态x(t) 的离散时间TP-BVP。

重新定义一个由拉格朗日乘子μ和输入向量组成的离散化的控制输入向量U(t) ∈RmuN:

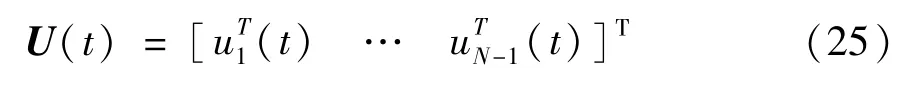
将FB 函数作为互补条件,与最优化条件组成约束条件为

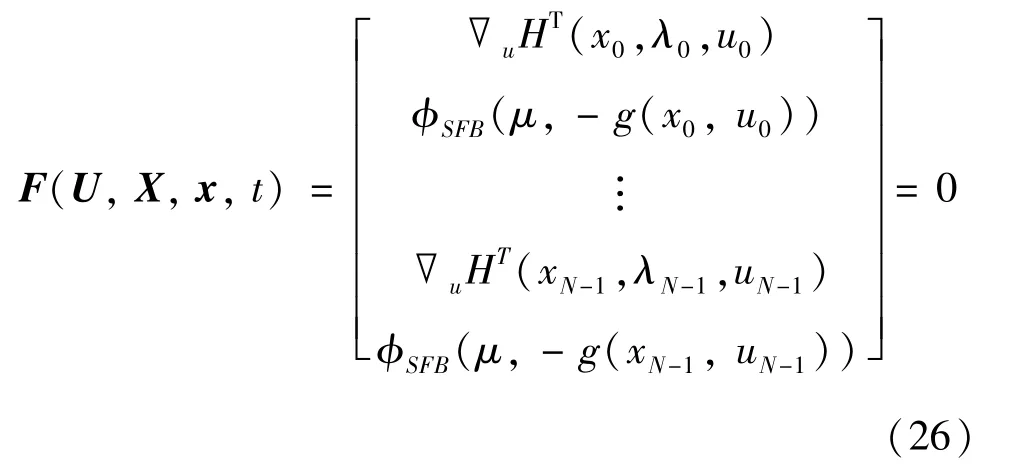
相比于将误差仅分布在F=0 中,多重打靶法倾向于将误差同时分布在状态向量和共态向量中时,预计将会减小整体误差,即算法的精度会提高,有利于非线性系统的稳定性及收敛性。使用多重打靶算法时,需要将状态向量x、拉格朗日乘子μ、共态向量λ以及控制输入向量u视为独立变量。将连续状态向量和共态向量组合构建出一个新的向量

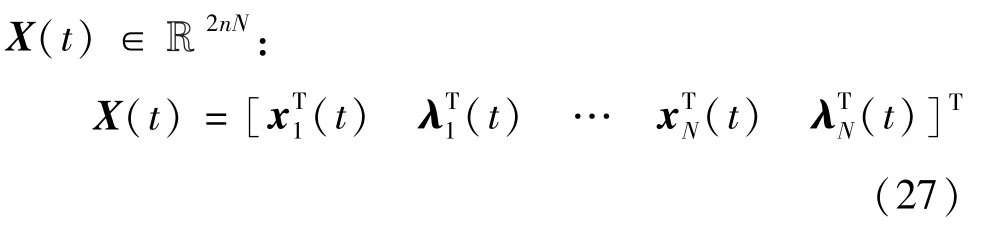
建立状态和共态向量的代数约束:

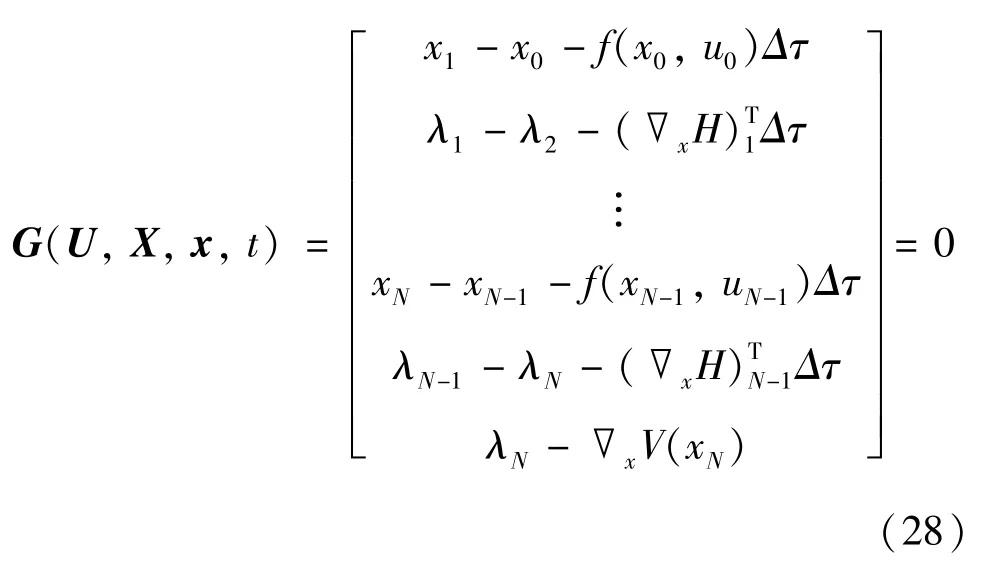
通过建立上述约束,可以保证系统总是相对之前获得的预测条件进行计算,并且其初始状态将不会在整个时域T上进行积分。

2.4 优化求解

针对方程组式(26)和式(28),利用t为参数的连续法[26],同时进行延拓。首先需对约束条件F与控制输入向量U进行拆分处理:

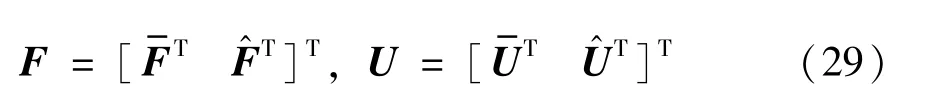
同时,拆分时需要满足以下3 个条件:

(1) 作为消去与的必要条件之一,和的维数必须相同。

(2) 在分解时,约束G中不包含中的任何元素,约束F^ 中不包含任何关于X的元素。且在连续状态方程中没有中的任何元素。在哈密顿量H中不包含与状态向量交叉的项,对应此式即为在状态方程中不存在虚拟输入u及拉格朗日乘子μ。

(3) 为了在某一时间步的输入向量u及拉格朗日乘子μ仅在其对应时间步的哈密顿量H中出现,要求当与任意向量点乘时有解,且计算边界较小。

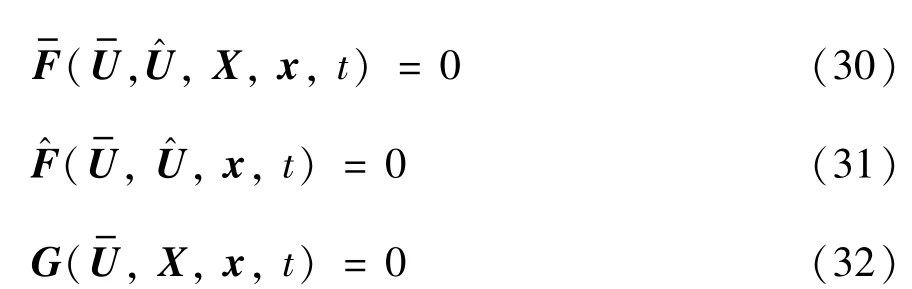
对上述的3 个约束使用延拓法进行关于t的延拓,带入初始条件(0)、(0) 及X(0) 进行积分操作求解,得到:

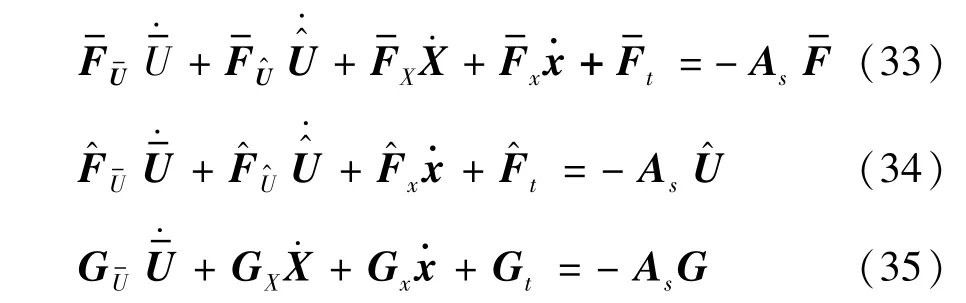
其中As是正稳态矩阵。对式(33)～式(35)进行合并化简带入后,得到关于的线性方程:

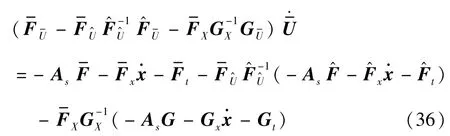
为了避免逆矩阵带来庞大计算量,提出一种消除式(36)中的矩阵方法。引入一个虚拟变量ρk∈R2nN,满足,对其进行移项处理后有:

计算中,为了减少雅可比矩阵与线性方程相乘时带来的计算量,引入前向差分近似概念:

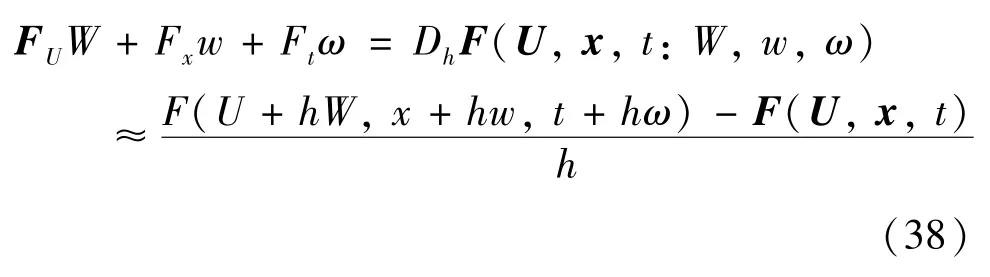
式中,h表示前向差分步长,是一个小的正实数。利用前向差分近似处理式(37)有:

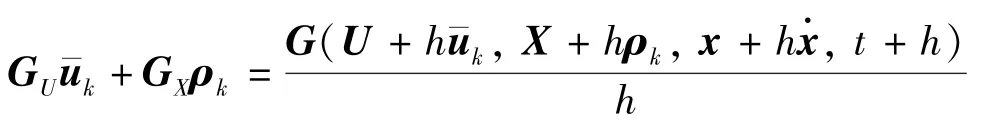
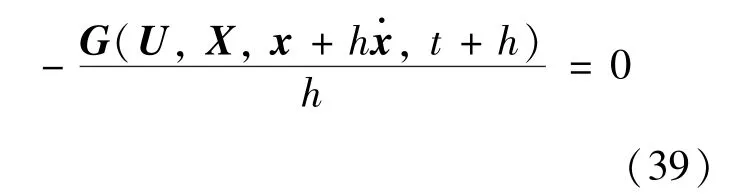
化简可得:

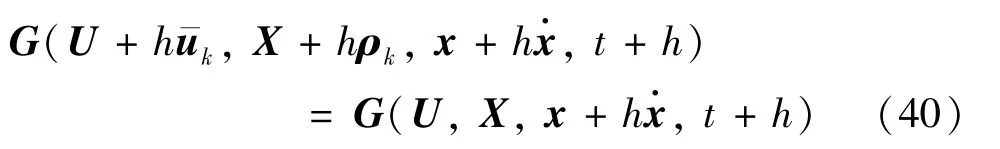
在上述算法中已经提到,多重打靶法相比于原算法的改进之处,在于将误差同时分布到了状态向量和共态向量约束G中来减小整体误差。取误差向量表示为,对X满足:

定义一个映射B:RmN ×R2nN ×Rn ×R →R2nN,当U、x、t均确定时,B即为G的逆映射。由此,根据G的定义可得X=B(,E,x,t),且满足:

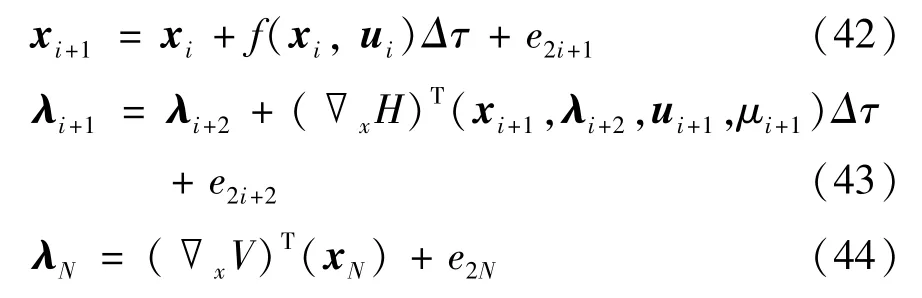
通过此方法分别求得xi、λi后,即可通过递归计算求得B(,E,x,t),结合式(40)可以推导出:

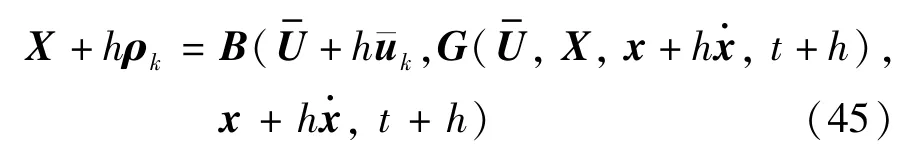
对式(45)进行变换即可求得虚拟变量ρk,即可得到的值为

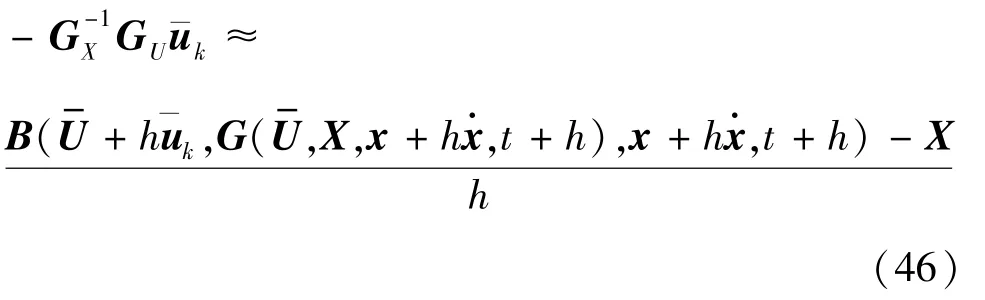
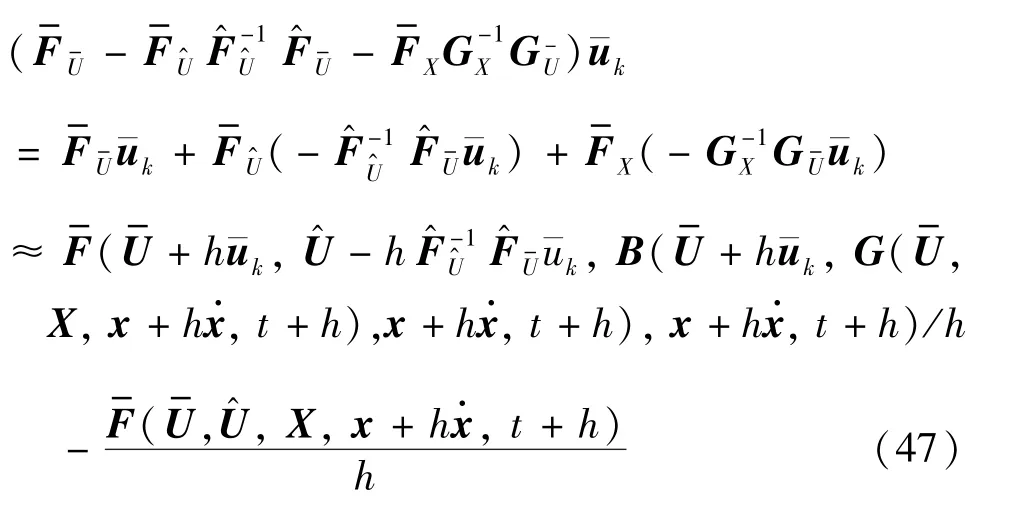
上式虽然看似比较复杂,其实可以仅仅使用和B直接表示获得。

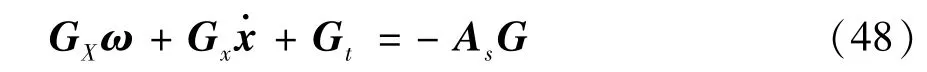
对式(48)前向差分近似处理,得到:

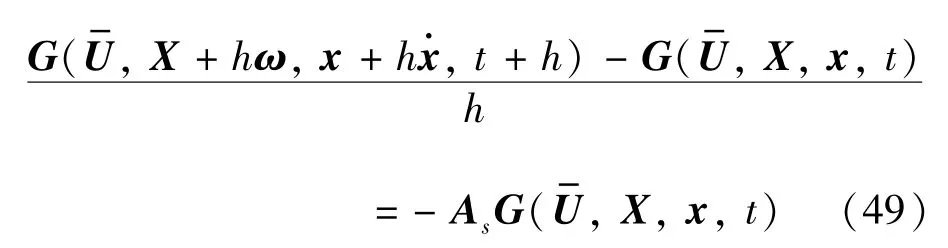
化简后可得:

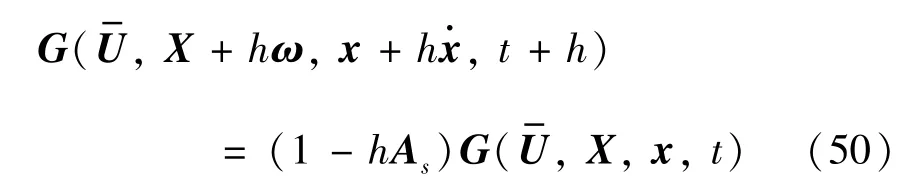
根据上文所提的映射B,可以解得X+hω:

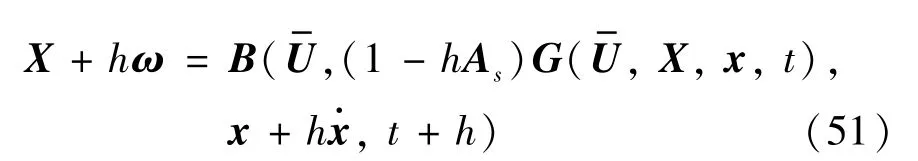
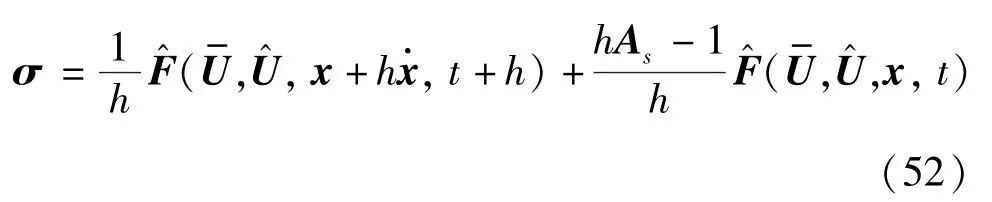
由条件式(3)可知求解时计算边界很小,则式(36)右侧可以化简为

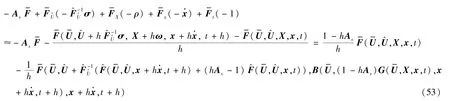
综上,利用GMRES 算法对式(36)计算,快速求解获得。根据映射B及式(51),无需通过GMRES即可求得:

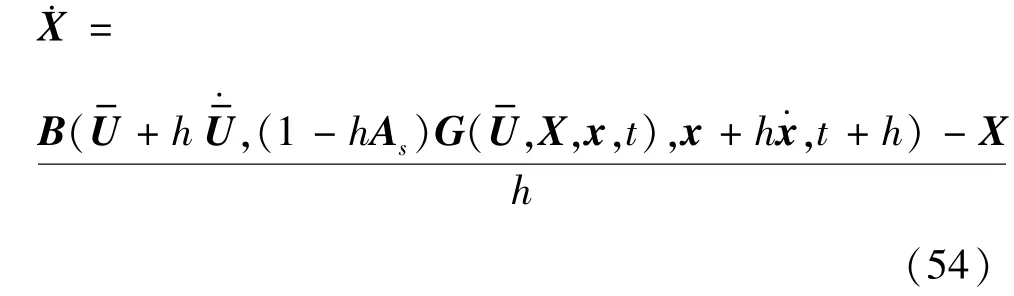
根据式(34)可以解得:

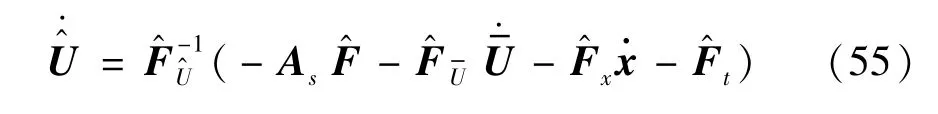
在求得及之后,利用欧拉法(Euier)分别对其积分,更新控制输入U及状态向量X。

2.5 算法优化

多重打靶法的引入提高算法精度的同时,也带入了较为沉重的计算负担,主要集中在对每个时间步上非线性函数的雅可比矩阵的计算,比使用传统的GMRES 算法计算效率大幅提高。然而,该算法在对Hessenberg 矩阵进行正交分解时,依然涉及比较复杂繁琐的计算。因此,此算法在此处仍可进行优化。很多学者都提出了基于GMRES 算法的改进算法[27]。然而在一些情况无法避免地出现震荡现象。本文通过对Krylov 子空间的第2 个元素开始进行Arnoldi 过程处理,将原本的n × m维Hessenberg矩阵,改进为上三角矩阵Wk,避免正交分解处理,就能减少计算量。

考虑非线性方程:

为提高该控制算法的稳定性[28],可将子空间Kk(A,r0)=span{r0,Ar0,…,Ak-1r0} 的元素,即传统GMRES 算法的基替换为如下形式:

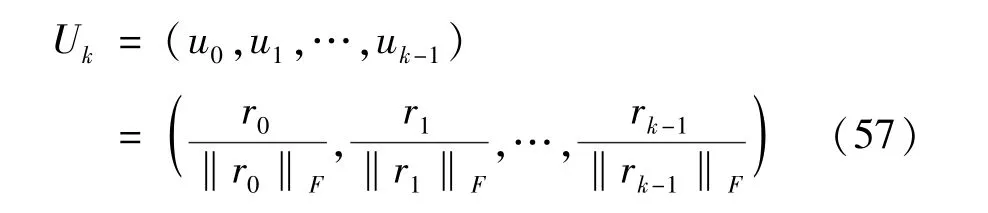
其中初始参量为r0=b -AM0,其余参量满足ri=b-AMi∈Kk(A,r0)。将向量组Uk进行Arnoldi 处理:

式中Vk=(v1,v2,…,vk)T,为AKk(A,r0) 的标准正交基,令wi,j=(Auj,vi) 为上三角矩阵,取‖vj+1‖F=wi,j+1,求得的Wk为上三角矩阵,取Mk=M0+tk,其中tk∈Uk,即tk=Ukyk,yk∈Rk×1。假设经过k次迭代后,有

通过调整yk使得rk与AUkyk垂直时,‖rk‖F取得最小值,即

结合式(59)可得到:

求得近似解:

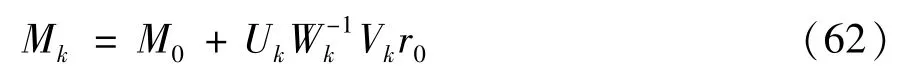
改进之后的GMRES 算法减少了正交分解所带来的额外的计算需求,提高了算法的运行效率与稳定性。

3 仿真结果

在仿真模拟中使用为个人电脑的CPU 为英特尔Core i7 -9750H,6 核,时钟频率为4.5 GHz。在Matlab 2016a 环境下对圆形(固定曲率)与伯努利双纽线(变曲率)路径进行跟踪仿真模拟。

圆形路径定义如下:

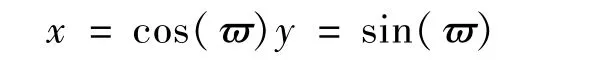
式中,ϖ为路径参数,确定了虚拟目标在世界坐标系下的位置,初始状态和终端状态分别选取为

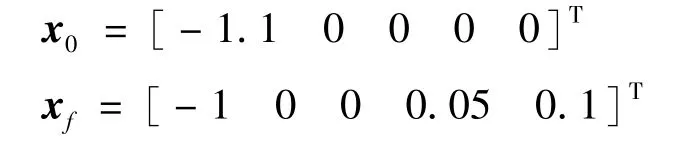
初始输入为u=[0 0]T,仿真参数设置中,T=1 s,N=10,采样时间选择为Δτ=0.1,权重矩阵取:

约束参数中设置vmin=0 m/s,vmax=0.16 m/s,ωmax=0.8 rad/s,u1min=-0.08 m/s2,u1max=0.08 m/s2,u2min=-0.6 rad/s2,u2max=0.6 rad/s2。

伯努利双纽线路径定义为

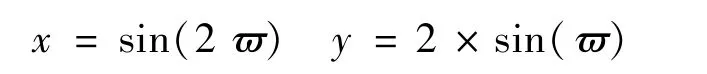
初始状态与终端状态分别选取为

初始输入为u=[0 0]T,仿真参数设置中,T=1 s,N=10,采样时间选择为Δτ=0.1,权重矩阵取:

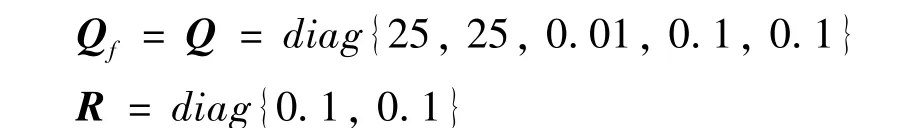
约束参数中设置vmin=0 m/s,vmax=1 m/s,ωmax=0.8 rad/s,u1min=-0.2 m/s2,u1max=0.3 m/s2,u2min=-0.4 rad/s2,u2max=1 rad/s2。

其他相关参数为ε=0.01,h=0.001,As=Dh=1/h=1000,m=1.5,R=0.048,I=0.0348,C/GMRES 算法内部参数设置初始控制输入与乘子的误差容限rtol=1.0e-8,GMRES 的迭代数kmax=10。

仿真中引入另外2 种算法与本文所提算法进行对比。第1 种选择Matlab 自带的SQP 算法;第2 种为MSC[29]算法,通过障碍函数法对不等式进行处理;第3 种为本文提出的改进算法(NMPC)。其中ref 表示虚拟目标的参考路径。跟踪误差表示为,最优性误差‖F‖,定义为式(26)中F的2 -范数。

对圆形路径的跟踪仿真中,设定运行时间为10 s,由图3(b)可知,针对固定曲率的路径进行跟踪,3种算法都表现出良好的跟踪效果,在稳定跟踪后,跟踪误差均能控制在0.01 m 范围内。相比之下,本文所述算法的跟踪结果在0.5 s 时已经跟踪至目标路径且趋于稳定,最优性误差峰值最低,比另外2 种算法更为敏感。从图3(d)～(g)可知,跟踪速度与加速度在接近3 s 时开始收敛,达到期望值,3 种算法表现相当。

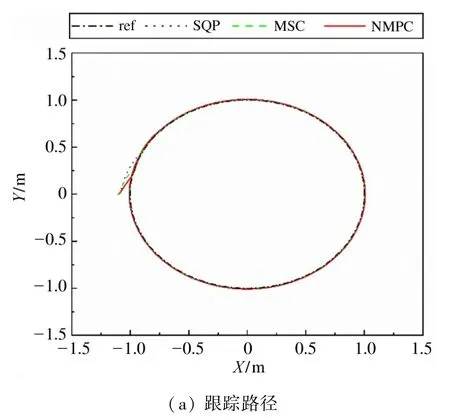
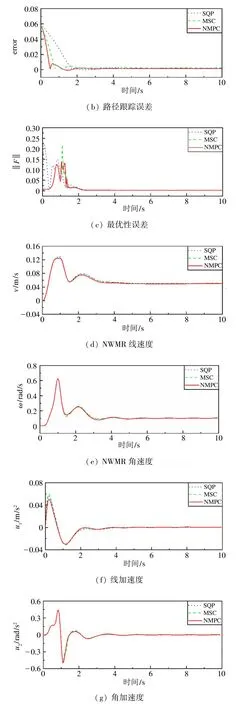
图3 圆形路径跟踪仿真结果

对伯努利双纽线路径跟踪仿真中,设定仿真运行时间为10 s,由图4(a)和(b)可知,针对变曲率路径3 种控制效果差异较为明显。SQP 算法在曲率变化较大的区域会出现较为明显的跟踪误差,且其最优性误差峰值较大,对于拐角区域的路径并不敏感。相比较而言MSC 与本文的算法控制效果更佳,在拐角区域基本可以稳定跟踪。同时针对不同预测步长N,对3 种算法的控制更新平均计算时长和平均误差进行了仿真,结果如表1 和表2 所示。在N=5的条件下,MSC 与SQP 满足在采样周期中进行跟踪。然而,随着采样步长的增加,两种算法的计算速率开始降低,在N=10 的条件下,平均计算时间分别达到了0.132 s和0.2134 s,都超过了采样周期,代表着其无法在采样时间要求0.1 s 内获得NMPC 的最优控制输入,在实际工作时可能无法准确进行路径跟踪。相较而言,本文算法在计算速率上展现出了优势,即使在采样步长N=50 的情况下,依旧可以仅消耗采样时长10% 以内的时间有效求解NMPC,同时满足运行的实时性要求,虽然相比较MSC 其误差有所增加,但依旧满足精度要求。在针对更加复杂的非线性系统时,本文所述算法的提升会更加显著。

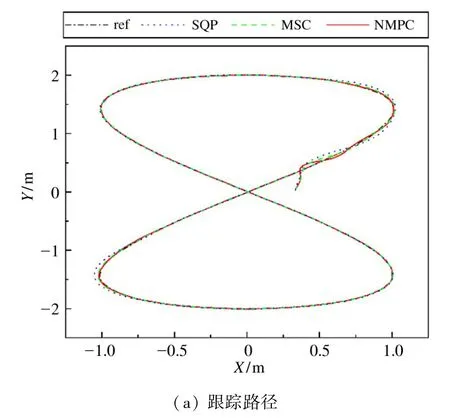
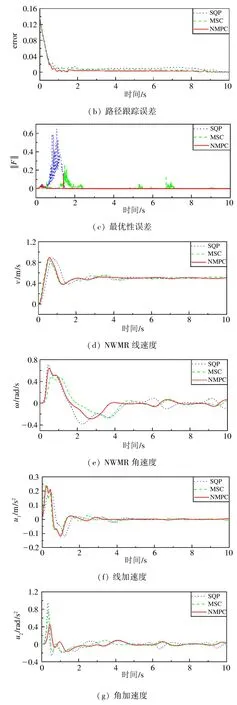
图4 伯努利双纽线路径跟踪仿真结果

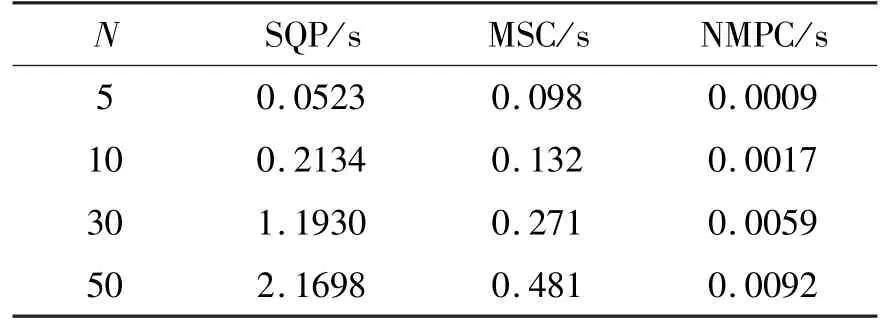
表1 平均计算时长

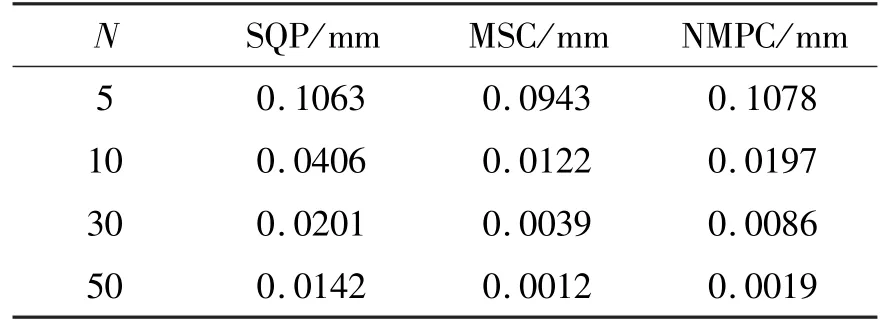
表2 平均跟踪误差

4 结论

针对非完整移动机器人路径跟踪问题,本文通过定义NWMR 与虚拟目标的跟踪误差,建立Bolza形式的NMPC 最优控制问题框架。引入半平滑函数,将不等式约束融入最优化必要条件之中,通过使用GMRES 算法计算求解广义哈密顿函数。同时引入多重打靶法及改变残量求取方式以提高运算精度及运算速率。仿真结果表明,本文所述的控制算法可以在满足实时性的前提下,保证更高的计算效率及精度。

然而本文并未对实际环境中的外界因素,如摩擦圆极限条件下的打滑情况[30]进行考虑,因此针对如何提高该算法的鲁棒性将是未来的研究方向。