区间集非交换剩余格广义Fuzzy滤子的构造性刻画
乔希民,谢小军,罗俊丽,吴洪博
(1.广州工商学院 通识教育学院,广东 佛山 510850;2.商洛学院 数学与计算机应用学院,陕西 商洛 726000;3.陕西师范大学 数学与信息科学学院,西安 710062)
美国计算与控制论专家Zadeh于1965年所创立的模糊集理论[1],极大地促进了建立在模糊集理论上的模糊演绎推理逻辑体系和与之相匹配的模糊逻辑代数分析的发展。波兰数学家Pawlak于1982年提出的粗糙集理论[2],是对知识库研究化为对等价关系的研究,是对知识库的约简化为对等价关系族的约简,最大限度地克服了模糊集中隶属度论域函数同类隶属关系的主观性,从而用知识库中上近似集与下近似集的清晰知识来表述任意“不确定性”与“含糊”的不一致性,讨论基于知识粒度的模糊相似关系的上、下近似及数学结构、模糊粗糙集的数学特征,显现了Zadeh集与Pawlak集的不可区分性、近似空间、知识表达系统等核心概念,在云计算、云模型、云变换(粒计算理论与方法)、云推理、云控制、数据场与拓扑势、三支决策分析等人工智能方面的广泛应用[3-7]。Yao等人从粗糙集的近似结构出发,既将描述部分已知概念的信息不完备性得以精确地给出,又将下近似集和上近似集满足特定条件的语义解释相结合,抽象概括为区间集概念[8-11],完善了区间理论体系。文献[12]主要介绍了三支决策理论、模型与方法,基于模糊集、粗糙集、区间集构造三支决策,基于直觉模糊集与区间集的三支决策研究,形式概念的三支表示,粗糙模糊集与模糊三支决策等。文献[13]研究了基于经典集、模糊集、粗糙集三种语境下的二元关系的模糊粗糙近似算子的构造性数学结构,以及近似算子的公理化刻画等,充分体现区间集理论在三支概念分析与决策计算等领域中的实践[14-16]。滤子理论[17-21]既是研究模糊逻辑演绎推理系统可视为代数滤子的镜像,又是众多学者从不同视域提出性质迥异的滤子概念,拓展了模糊逻辑代数分析的研究路径。文献[22]研究了逻辑代数上的滤子(理想)理论,EQ-代数上的拓扑结构及拓扑EQ-代数,逻辑代数及其超结构上的态理论、内态理论和广义态理论,而基于非可换逻辑代数均含有共同的非交换剩余格这一本质的基础性代数结构。
本文将区间集思想和滤子理论应用于非交换剩余格,在给出区间集非交换剩余格的定义和文献[23-26]的基础上,构造性地研究了区间集非交换剩余格广义Fuzzy滤子的代数结构,又进一步讨论了它们之间的等价性表示定理的特征刻画。
1 预备知识
定义1[9-11]设A=[Al,Au],其中Al,Au是任意经典集合且Al⊆Au。区间集用下近似集和上近似集对来表示,定义如下:设U为论域,2U是U的幂集,那么区间集上2U的子集形式为:A=[Al,Au]={A∈2U|Al⊆A⊆Au},称其为一个闭区间集。闭区间上的所有区间集的集合记为I(2U)={[Al,Au]|Al,Au⊆U,Al⊆Au}。
注1 当Al=Au时,区间集A=[Al,Au]成为经典集合A,其全集U=[U,U],空集∅=[∅,∅]。

引理1 设A,B,C∈I(2U),则下列各式成立:






(2) 〈I(2U),⊗,U〉是以U为单位元的半群;

则称I(2U)为区间集上非交换剩余格。
定义4[23-26]若I(2U)中的算子满足交换性,则称I(2U)为区间集交换剩余格。
性质1[23-26]设∀X,Y,Z∈I(2U),则有
(1) ⊗:I(2U)×I(2U)→I(2U)是单调递增的;













定义5[23-26]设I(2U)是区间集非交换剩余格,J⊆I(2U),J≠∅,如果∀X,Y∈I(2U),有

(2) 若X,Y∈I(2U),则X⊗Y∈I(2U),
那么称J为I(2U)上的一个滤子,所有滤子之集记为J(I(2U))。

命题1[23-26]设I(2U)是区间集非交换剩余格,J⊆I(2U),J≠∅,则J是滤子当且仅当J满足
(1)U∈J;

定义6[23-26]设I(2U)是区间集非交换剩余格,J:I(2U)→[∅,U]是一个映射,则J为I(2U)的模糊子集。全体模糊子集之集记为F(I(2U))。

定义8[23-26]设I(2U)是区间集非交换剩余格,X∈I(2U),J∈F(I(2U)),若J满足
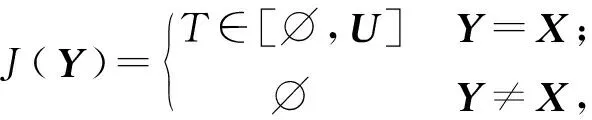
则称J为I(2U)上的一个模糊值,记为XT,其中X是XT的支撑,T为XT的值,记为G(X,T)。


注3P(X)与T的线性和记为P(X)⊕T;P(X)与T的线性差记为P(X)⊖T。
定义9[23-26]设∀X,Y∈I(2U),J∈F(I(2U)),如果J满足以下条件:


则J称为I(2U)上的Fuzzy滤子。
命题2[23-26]设J∈F(I(2U)),则J是I(2U)上的一个广义Fuzzy滤子的充要条件为:


2 I(2U)上广义Fuzzy滤子的构造
定义10[25]设I(2U)是区间集非交换剩余格,F∈F(I(2U)),若满足


则称F为I(2U)上的广义Fuzzy滤子。全体广义Fuzzy滤子之集记为FF(I(2U))。
定理1 设I(2U)是区间集非交换剩余格,F∈F(I(2U)),则F为I(2U)上的一个广义Fuzzy滤子的充要条件是F满足



又对∀X,Y∈I(2U),由性质1中之(6)和定义10中之(1)得


充分性:分以下两步完成:



定理2 设I(2U)是区间集非交换剩余格,F∈F(I(2U)),则下述条件等价:
(1)F是I(2U)上的一个广义Fuzzy滤子;


证明 由(1)推(2)。设F是I(2U)上的一个广义Fuzzy滤子,又设X,Y,Z∈I(2U)且X⟹(Y⟹Z)=U,则由定理1有




由(1)推(3),仿上述由(1)推(2)可得。故定理2成立。
定理3 设I(2U)是区间集非交换剩余格,F∈F(I(2U)),则F为I(2U)上一个广义Fuzzy滤子的充要条件是:∀T∈((CI,U],G(F,T)为I(2U)上的一个广义滤子。这里G(F,T)是非空的。
证明 必要性:假设∀T∈((CI,U],G(F,T)是非空的,分以下两种情形证G(F,T)是一个广义滤子。



故由命题1知G(F,T)是I(2U)上的一个广义滤子。
充分性:分以下两步完成:


故根据定理1知F是I(2U)上的一个广义Fuzzy滤子。

证明 必要性:设∀T∈(∅,CI],且H(F,T)是非空的,分以下两步:



H(F,T)。
故依据命题1知H(F,T)是I(2U)上的广义滤子。
充分性:分以下两步完成:



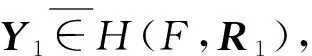
故依据定理1知F是I(2U)上的广义Fuzzy滤子。
3 结语


