Douglas-Rachford分裂算法的Mann迭代形式的收敛性及其应用

赵 旭

(西华师范大学数学与信息学院，四川南充 637009)

0 引言

Lions和Mercier在文献[1]中介绍了Douglas-Rachford分裂算法，这个算法是应用于寻找两个算子和为零的一种有效方法，即

∃x∈H，使得0∈A(x)+B(x).

这里的算子A:H→2H，B:H→2H都是极大单调算子.Douglas-Rachford分裂算法基于如下迭代形式：

其中初始值u0∈H，RA和RB为算子A，B的反射预解算子.

这个强收敛结果补充了文献[2]的结果.

Douglas-Rachford分裂算法是应用于寻找两个次微分算子和为零的一种有效的方法，这样的单调包含问题可以用来表述凸优化问题的原最优性条件、对偶最优性条件、原对偶最优性条件、凸凹对策的平衡条件、单调变分不等式和单调互补问题.Douglas-Rachford算法在信号处理[12]、图像去噪[13]和统计估计[14]等方面显示出了巨大的应用潜力.Douglas-Rachford算法还可以推导出其他重要的分裂方法，如文献[15]中的交替方向乘子法(ADMM)、Spingarn的部分逆法以及文献[16]中的原对偶混合梯度法、线性化ADMM等方法.

在Lions，Mercier和Giselsson的启发下，本文考虑Douglas-Rachford算法的一个凸组合形式和Mann迭代形式的收敛性.基于文献[4]的迭代方法，可以证明得到Douglas-Rachford算法的一个凸组合形式是强收敛的，以及Douglas-Rachford的Mann迭代形式是弱收敛的.这个结论拓展了收敛的Douglas-Rachford算法的形式，并且对这个结论做了一个简单的应用，结合变分不等式，应用于一个法锥与强单调算子的和，可得到Douglas-Rachford算法的Mann迭代形式的弱收敛性.

1 预备知识

整篇文章中，设H是一个实的希尔伯特空间，用符号〈·，·〉表示内积，用符号‖·‖表示范数.用符号A:H→2H，表示A是H到H上的集值算子, 算子A的有效域表示为 dom(A)={x∈H|Ax≠φ},用符号A:H→H表示单值算子，此时dom(A)=H.若{xn}是H中的一个序列，称序列{xn}强收敛于H中一点x，若‖xn-x‖→0，当n→∞时；称序列{xn}弱收敛于H中一点x，∀y∈H,若〈y,xn〉→〈y,x〉，当n→∞时.把算子A的图表示为gra(A)={(x,u)∈H×H|u∈Ax}.算子A:H→2H的不动点集表示为Fix(A)={x∈H|Ax=x}.算子A的预解算子为JA=(Id+A)-1,算子A的反射预解算子为RA=2JA-Id.

定义1[3]称一个单值算子A:H→H为β-Lipschitz连续的，如果

‖Ax-Ay‖≤β‖x-y‖,∀x,y∈H

(1)

定义2[4]称一个单值算子A:H→H是一个非扩张算子，如果

‖Ax-Ay‖≤‖x-y‖,∀x,y∈H

(2)

通过上面，可以看出1-Lipschitz连续也叫做非扩张算子.当算子A:β-Lipschitz连续，并且β系数属于[0,1)，则把A称作一个Banach压缩算子.

定义3[4]称一个单值算子A:H→H为α-averaged，如果它可以被表示为

A=(1-α)Id+αV,并且α∈[0,1)

(3)

这里的Id:H→H表示的是一个恒等算子，V:H→H为一个非扩张算子.

定义4[4]称一个集值算子A:H→2H是β-cocoercive，β>0，如果

〈x-y,u-v〉≥β‖u-v‖2,∀(x,u),(y,v)∈gra(A)

(4)

定义5[3]称一个集值算子A:H→2H是μ-强单调，μ>0，如果

〈x-y,u-v〉≥μ‖x-y‖2,∀(x,u),(y,v)∈gra(A)

(5)

定义6[3]C⊆H的法锥NC定义为：

(6)

定义7[3]称一个集值算子A:H→2H是单调的，如果

〈x-y,u-v〉≥0,∀(x,u),(y,v)∈gra(A).

(7)

2 引理

如下引理在后面的证明中有重要作用.

引理2.1[4]设x∈H,y∈H,α∈R，则有：

‖αx+(1-α)y‖2+α(1-α)‖x-y‖2=α‖x‖2+(1-α)‖y‖2

(8)

引理2.2[4]设集合C是H中的一个非空闭凸子集，算子T:C→H是非扩张的，则T的不动点集Fix(T)也是闭凸集.

引理2.3[5]若{xn}是H中的一个序列，存在一个非空闭凸集C⊆H满足下列条件：

(2)若序列{xn}的子序列{xnj}弱若收敛于x*，且x*∈C,

则存在x0∈C,使得{xn}弱收敛于x0.

引理2.4[2]设β≥μ>0，若算子A、B满足下列四种情况之一：

(c)单值算子A:H→H是β-Lipschitz且μ-强单调的;

(d)单值算子A:H→H是单调且β-Lipschitz连续的，集值算子B:H→2H极大单调且μ-强单调的；

证明：此结论在[3]和[5]中已有详细证明.

引理2.5[4]设集合C是H中的一个非空闭凸子集，算子T:C→H是非扩张的，{xn}是集合C中一个序列，x为集合C中一点.若{xn}弱收敛于x，且xn-Txn→0，则x∈Fix(T).

3 主要结论

定理3.1假设算子A、B满足引理2.4(a)-(d)中任一种条件，且α∈(0,1)，则下列结论成立：

证明：(1)由引理2.4知TDR是关于常数κ的Banach压缩算子，且κ∈(0,1)；即

‖TDRx-TDRy‖≤κ‖x-y‖≤‖x-y‖,∀x,y∈H.

(9)

因此算子TDR:X→X是一个非扩张算子.则可以得到：

‖T′x-T′y‖=‖αx+(1-α)TDRx-αy+(1-α)TDRy‖，

=‖α(x-y)+(1-α)(TDRx-TDRy)‖，

≤α‖x-y‖+(1-α)‖TDRx-TDRy‖，

≤α‖x-y‖+(1-α)κ‖x-y‖，

=[α+(1-α)κ]‖x-y‖.

(10)

根据α∈(0,1)，κ∈(0,1)可知[α+(1-α)κ]∈[0,1)，所以T′是一个Banach压缩算子，由Banach压缩不动点定理知，{un}强收敛于H中一点u.

(1)设xn+1=Tnxn=αnxn+(1-αn)TDRxn，则{xn}弱收敛于S中一点x；

证明：由xn+1=Tnxn=αnxn+(1-αn)TDRxn，则Tn=αnId+(1-αn)TDR，并且TDR是非扩张算子，所以TDR是(1-αn)-averaged算子.由于算子TDR是非扩张的，根据引理2.2可知：算子TDR的不动点集Fix(TDR)是一个闭凸集.

取x*∈Fix(TDR)，由引理2.1及不等式性质有：

‖xn+1-x*‖2=‖αn(xn-x*)+(1-αn)(TDRxn-x*)‖2，

=αn‖xn-x*‖2+(1-αn)‖TDRxn-x*‖2-αn(1-αn)‖xn-TDRxn‖2，

≤αn‖xn-x*‖2+(1-αn)‖xn-x*‖2-αn(1-αn)‖xn-TDRxn‖2，

=‖xn-x*‖2-αn(1-αn)‖xn-TDRxn‖2.

(11)

由前面(11)式移向整理后可得到：

αn(1-αn)‖xn-TDRxn‖2≤‖xn-x*‖2-‖xn+1-x*‖2，

因此由上式得到：

(12)

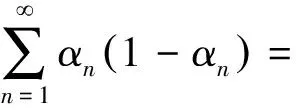
‖xn+1-yn+1‖=‖αnxn+(1-α)TDRxn-yn+1‖=‖αnxn+(1-αn)yn-yn+1‖，

=‖αn(xn-yn+1)+(1-αn)(yn-yn+1)‖，

≤αn‖xn-yn+1‖+(1-αn)‖yn-yn+1‖，

=αn‖xn-yn+1‖+(1-αn)‖TDRxn-TDRxn+1‖，

≤αn‖xn-yn+1‖+(1-αn)‖xn+1-xn‖，

≤αn(‖xn-xn+1‖+‖xn+1-yn+1‖)+(1-αn)‖xn+1-xn‖，

=‖xn-xn+1‖+αn‖xn+1-yn+1‖，

=‖xn-(αnxn+(1-αn)yn)‖+αn‖xn+1-yn+1‖，

=(1-αn)‖xn-yn‖+αn‖xn+1-yn+1‖.

(13)

对上述(13)式进行移向整理得到:

(1-αn)‖xn+1-yn+1‖≤(1-αn)‖xn-yn‖

(14)

由于{αn}⊂(a,b)⊂(0,1)，结合(12)式则可以得到：‖xn+1-yn+1‖≤‖xn-yn‖，

(15)

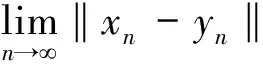
(16)

取序列{xn}的一个子序列{xnj}，使得xnj弱收敛于z.

根据(16)式可以得到：

(17)

结合(17)式和引理2.5知：z∈Fix(TDR)=S.

因此由引理2.3知：∃x0∈S，使得{xn}弱收敛于x0，即{xn}弱收敛于S中一点x0.

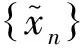
4 应用

设算子A:H→H是单调且β-Lipschitz连续的，β>0，

设算子F:H→2H是μ-强单调的，C⊆H为非空闭凸集.考虑变分不等式问题:

〈(A+F)x,y-x〉≥0，∀y∈C.

那么，若x为上述变分不等式的解，则：〈-A(x)-F(x),y-x〉≤0，

结合C的法锥的定义知：

-A(x)-F(x)∈NC(x)，

即：

0∈A(x)+F(x)+NC(x)，

(18)

命题4.1 设算子A:H→H是单调且β-Lipschitz连续的，β>0，算子F:H→2H是μ-强单调的，x∈C为变分不等式〈(A+F)x,y-x〉≥0的解，∀y∈C.令算子B=F+NC，则算子B:H→2H为极大单调且μ-强单调的.

证明：由于NC为集合C⊆H的法锥，则NC为极大单调算子，也满足单调的性质，即：

〈x-y,u-v〉≥0,∀(x,u),(y,v)∈gra(A).

又因为F为μ-强单调算子，即：〈x-y,F(x)-F(y)〉≥μ‖x-y‖2，因此B=F+NC也是极大单调算子.

〈x-y,B(x)-B(y)〉=〈x-y,F(x)+u-F(x)-v〉=〈x-y,F(x)-F(y)〉+〈x-y,u-v〉，

≥μ‖x-y‖2，

因此算子B为极大单调且μ-强单调的.

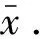
证明：由命题4.1知算子B为极大单调且μ-强单调的.又由于算子A:X→X是单调且β-Lipschitz连续的，β>0，则满足引理2.4中的条件(d).

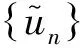
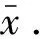
5 结语

在寻找两个算子和为0时，Douglas-Rachford算法是一种有效的办法.本文证明得到了Douglas-Rachford算法的凸组合形式收敛于实的Hilbert空间中一点，Douglas-Rachford算法的Mann迭代形式弱收敛于Douglas-Rachford算法的不动点集中一点.此外，将该方法应用于变分不等式问题，得到了Douglas-Rachford算法的凸组合形式的强收敛性以及其Mann迭代形式的弱收敛性.