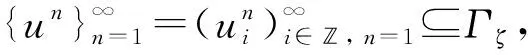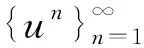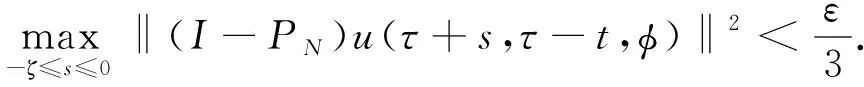一类具变时滞的Hopfield神经网络模型拉回吸引子的存在性
朱 双, 雷 婷
(西南交通大学 数学学院, 成都 611756)
0 引 言
目前, 关于Hopfield神经网络模型[1]动力学行为的研究已有很多结果[2-6], 关于不同格动力系统吸引子的研究也得到广泛关注. 文献[7-9]证明了二阶格动力系统吸引子的存在性及收敛性; 文献[10]考虑非线性时滞格系统, 证明了不存在解唯一性的系统所关联多值过程拉回吸引子的存在性. 本文在文献[11]的Hopfield神经网络模型中加入变时滞项, 对τ∈, 其离散方程为
其中u=(ui)i∈∈l2,μi,γi,λi,j和ζ均为大于0的正常数,n∈,ui,τ为初始值,fj是满足某些条件的非线性函数,ζ0(t)是时滞函数,g(t)=(gi(t))i∈是具有时间依赖性的序列, 并且φi∈C([-ζ,0],). 首先, 证明该方程连续非自治系统的存在性; 其次, 对非自治方程的解进行一致估计; 最后, 证明非自治方程(1)-(2)拉回吸引子的存在唯一性.
1 解的一致估计
首先, 定义
其对应的范数和内积分别为
记ut(t∈)为定义在[-ζ,0]上的函数, 其形式如下:
ut(s)=(ui,t(s))i∈=(ui(t+s))i∈=u(t+s),s∈[-ζ,0].
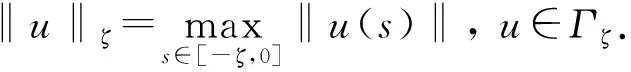
F(u)=-Θu+Υu+G,
其中
则方程组(1)-(2)可写成如下形式: 对∀τ∈,
为证明问题(3)-(4)拉回吸引子的存在性, 需做如下假设:
(H1)fi(0)=0,fi是全局Lipschitz连续的函数, 且具有Lipschitz常数L;
(H2) 存在大于0的常数a,b,B,d,D, 使得
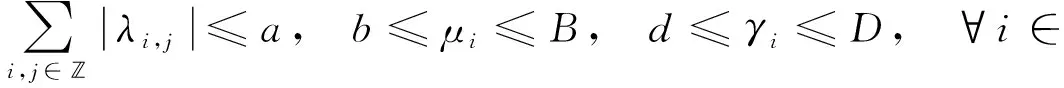
(H3) 令g(t)=(gi(t))i∈, 且

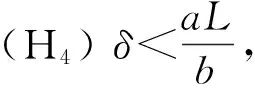
由假设(H1)~(H3)可知, 算子F:l2→l2是全局Lipschitz连续的, 且具有Lipschitz常数L.
显然, 由泛函微分方程理论可证得对每个φ∈Γζ, 均存在T>0, 使得问题(3)-(4)存在唯一的局部解ut(·,τ,φ)∈C([τ,T),Γζ). 因此, 可得:
定理1如果假设(H1)~(H3)成立, 则对任意的φ∈Γζ, 存在T>0, 使得问题(3)-(4)存在唯一的解ut(·,τ,φ)∈C([τ,T),Γζ).
引理1如果假设(H1)~(H4)成立, 则对任意的τ∈,T>0,φ∈Γζ和t∈[τ,τ+T], 均存在一个正常数c=c(τ,T,φ), 使得问题(3)-(4)的解u满足‖ut(·,τ,φ)‖ζ≤c.
证明: 在空间l2中, 对方程(3)与u做内积, 当t>τ时, 得
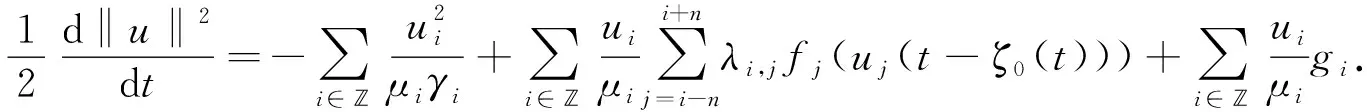
(5)
由假设(H2), 得
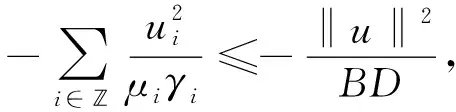
(6)

(7)
将式(6)~(8)代入式(5), 有
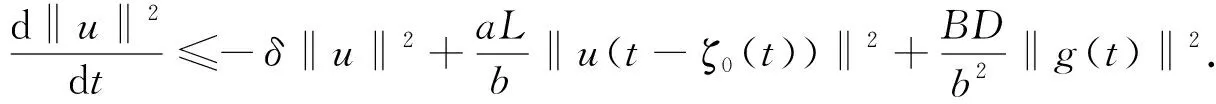
(9)
利用Gronwall不等式, 当t>τ时, 有
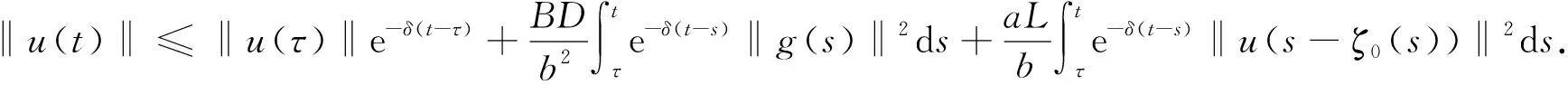
(10)
由假设(H4), 易知存在正常数β和Q, 使得当‖φ‖ζ≤Q时, 有
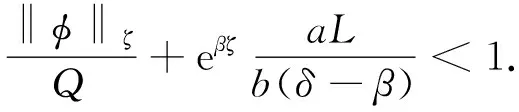
(11)
下面证明当t≥τ时, 下列不等式成立:
‖u(t)‖≤Qe-β(t-τ)+(1-ρ)-1J(t),
(12)
其中
首先, 证明当q>1时, 有
‖u(t)‖ (13) 假设不等式(13)不成立. 事实上, 由于‖φ‖ζ≤Q和‖u(t)‖是连续的, 因此当t*>τ时, 必有如下不等式成立: ‖u(t*)‖≥qQe-β(t-τ)+(1-ρ)-1J(t),t≥τ, (14) 且 ‖u(t)‖≤qQe-β(t-τ)+(1-ρ)-1J(t),t≥τ,τ-ζ≤t (15) 所以, 根据式(11),(12),(14),(15), 有 与式(14)矛盾, 即不等式(13)成立. 其次, 令q→1, 则不等式(12)成立. 证毕. 由引理1可知, 对任意的T>0, 在区间[τ,τ+T)上, 问题(3)-(4)的解都是有定义的, 表明局部解u是一个全局解. 取t∈, 在上定义一个变换: κt(τ)=τ+t, ∀τ∈. (17) 则{κt}t∈作用在上是一个群. 对于问题(3)-(4), 定义映射 Π:+××Γζ→Γζ. 取t∈+,τ∈,uτ∈Γζ, 令 Π(t,τ,uτ)=ut+τ(·,τ,uτ), (18) 其中 ut+τ(s,τ,uτ)=u(t+τ+s,τ,uτ),s∈-[ζ,0]. 由解的唯一性可知, 对任意的t,s∈+,τ∈,uτ∈Γζ, 有 Π(t+s,τ,uτ)=Π(t,s+τ,Π(s,τ,uτ)), 即在Γζ上Π是一个连续非自治的动力系统. 引理2假设(H1)~(H4)成立, 对任意的τ∈且, 问题(3)-(4)的解均满足 (19) 证明: 首先, 在式(9)中分别用ω和τ-t代替t和τ, 则当ω>τ-t时, 有 定义函数: Φ(ω)=eβω‖u(ω,τ-t,φ)‖,ω≥τ-t-ζ, (21) (22) 其次, 证明 Φ(ω)≤Ψ(ω),ω≥τ-t. (23) 假设不等式(23)不成立, 则必有ω*>t-τ, 使得 Φ(ω)<Ψ(ω),ω∈[τ-t-ζ,ω*), (24) Φ(ω*)=Ψ(ω*), 为引导学生进行更加积极有效的讨论,课程论坛分为精彩内容分享、章节讨论、在线客服三大公共版块和各班自由讨论区这一班内版块。其中,“精彩内容分享”这一版块主要汇聚了学习者的精彩讨论内容,供学习者在学习中参考,从而达到知识共享、转化和生成的目的;“章节讨论”版块要求师生讨论具体的章节内容或者某一知识点,缩小讨论范围,让细节更加立体,讨论更有针对性,也更为有效;“在线客服”则主要是平台技术人员对学习者在学习中遇到的系统问题和对课程平台的建议进行及时解答回复。 (25) 其中 ω*≜inf{ω>τ-t|Φ(ω)>Ψ(ω)}, 并且存在一个充分小的正常数Δω, 使得 Φ(ω)>Ψ(ω),ω∈(ω*,ω*+Δω). (26) 计算Φ(t)在ω*时的右上导数, 有 根据式(20), 有 由于在区间[τ-t-ζ,+∞)上,Ψ(ω)是单调递增的, 即根据式(24),(25), 得 Φ(ω*-ζ0(ω*))<Ψ(ω*-ζ0(ω*))<Ψ(ω*)=Φ(ω*), (29) 因此有 ‖u(ω*-ζ0(ω*),τ-t,φ)‖≤eβζ‖u(ω*,τ-t,φ)‖. (30) 根据假设(H1)及式(28),(30)得 (31) 与式(27)矛盾, 即不等式(23)成立. 于是, 当t>ζ, -ζ≤ξ≤0时, 有 证毕. 引理3假设(H1)~(H4)成立, 对于τ∈和, 存在T=T(τ,)>ζ和M=M(τ), 使得对任意的t≥T和φ∈, 问题(3)-(4)的解u均满足 (33) 由假设(H2), 有 (35) (36) 根据式(35)~(37)得 (38) 与引理2的证明过程相似, 对任意的t>ζ和-ζ≤ξ≤0, 有 (39) (40) 再根据假设(H3), 存在一个M=M(τ,ε)>0, 使得对所有的k≥M, 有 (41) 于是, 由式(39)~(41), 得 (42) 证毕. 引理5如果假设(H1)~(H4)成立, 则在l2中对任意的τ∈和)>ζ, 使得问题(3)-(4)的解u满足uτ(·,τ-t,φ)是等度连续的. 证明: 定义Pku=(u1,u2,…,uk,0,0,…),u∈l2且k∈. 由引理3可知, 当ε>0时, 存在T=T(τ,ε)>ρ和足够大的正整数N=N(τ,ε), 使得对所有的t≥T, 有 (43) 令u1=PNu.对所有的t≥T, 有 (44) 其中c=c(τ)是一个正数.不失一般性, 假设s1,s2∈[-ζ,0], 0 即存在一个常数ρ=ρ(ε)>0, 使得如果|s1-s2|<ρ, 则 根据式(43), 对所有的t≥T, 有 证毕. 证明: 对于τ∈, 定义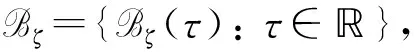
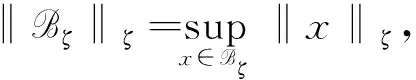
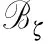
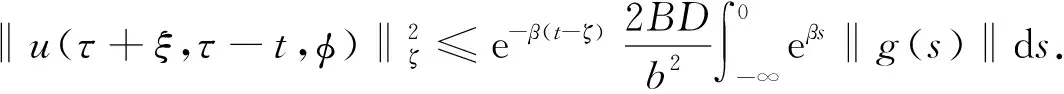
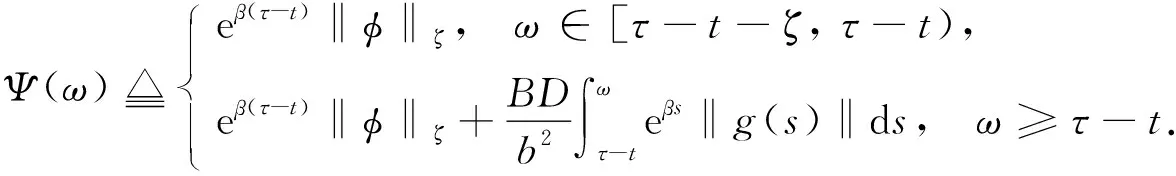
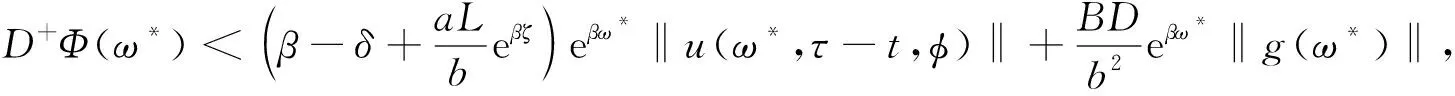
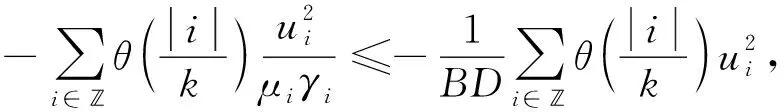
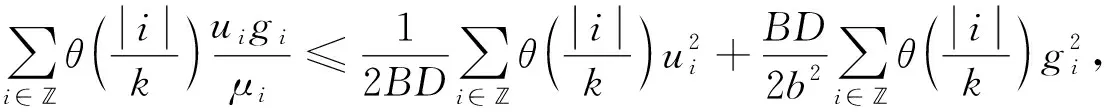
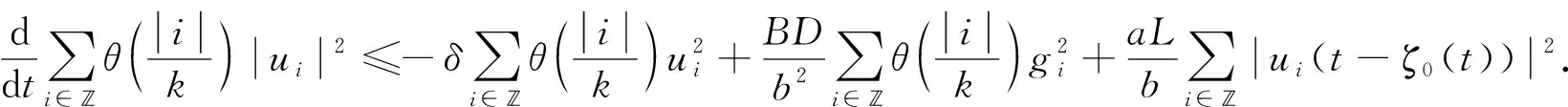
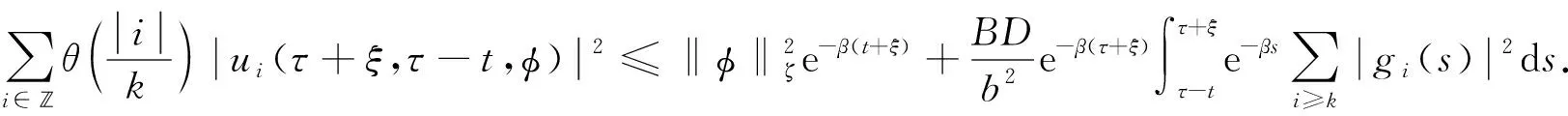

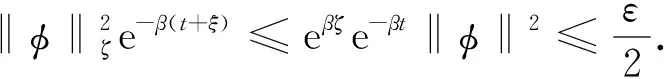
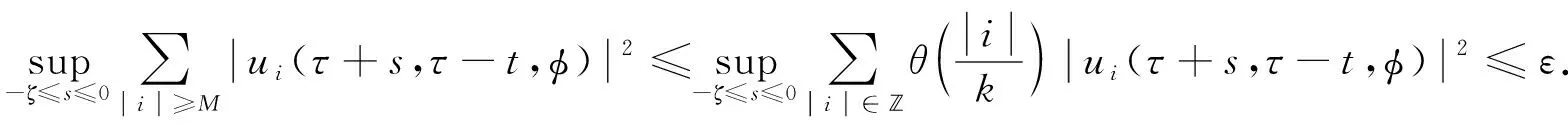
2 拉回吸引子的存在性