带斜向肋板的夹层结构抗侵彻性能研究
沈超明,陈豪杰,周 红,张 飞,谭 坤,王金友
(1. 江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003;2. 江苏现代造船技术有限公司,江苏 镇江 212003;3. 上海涟屹轴承科技有限公司,上海 201400)
0 引 言
当弹体与侵彻目标之间存在一定的倾角和攻角时称为斜侵彻。不同于垂直侵彻,斜侵彻过程中由于弹体所受的非对称力,给予弹体一个偏转力矩,可消耗更多弹体动能[1]。
夹层板作为一种复合材料,相对于单一的船用钢而言,具有强度高、质量轻、结构简单等优点[2-3],近年来在交通运输、工程防护、国防工业等领域得到广泛的应用。目前高分子材料与泡沫金属作为夹层板芯材的热门研究对象,芯材从单一板材演变成阵列结构,如蜂窝状、波纹状、桁架等拓扑结构[4-6]。M.halami-Choobar等[7-8]使用Ls-dyna数值仿真软件,研究了不同结构形式、不同芯材的夹层板在高速弹体冲击下的动态响应。葛超等[9]为研究弹体头部对斜侵彻弹体路径的影响,设计了3种不同头部形状及不同头部组合材料的弹体,并进行了中厚钢靶侵彻实验。结果表明,影响弹体偏角因素的权重由大到小为弹头形状、弹头材料和弹体初速度。
本文提出一种新型夹层结构,以尼龙为芯层,并在夹层中设置与面板相连的斜向钢质肋板,迫使正侵彻弹体在撞击斜肋板后产生一定程度的偏航,同时尼龙芯层吸收大量的弹体动能,从而有效提升夹层结构的抗侵彻性能。本文结合实验,对不同斜向肋板角度下的夹层结构进行数值模拟分析,探究该夹层结构抗侵彻性能与肋板角度、弹头形式的相关性。
1 夹层结构抗侵彻性能数值分析方法
1.1 数值计算模型的建立
夹层结构模型长120 mm、宽120 mm,厚32 mm(上下面板、上下肋板、肋板长度以及尼龙厚度分别为1 mm,1 mm,20 mm,30 mm),肋板角度为面板与肋板夹角,见图1。
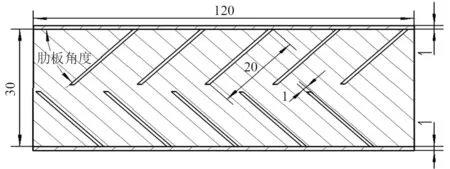
图1 夹层结构尺寸外形图Fig. 1 The dimension of sandwich structure
在Ansys/Ls-dyna程序中进行建模,使用Solid164实体单元建立1/2模型。对称面设置为对称约束,靶板四周设为固定约束。破片与靶体破坏中心区域用0.5 mm网格尺寸,其余网格尺寸为1 mm。接触算法为面面侵蚀接触,在2个相互接触的part赋予抗拉强度和剪切强度,模拟尼龙芯材与钢板、肋板之间的界面影响,数值仿真模型见图2。

图2 数值仿真模型Fig. 2 The model of numerical simulation
1.2 材料动态本构方程的拟合及参数确定
1.2.1 钢材本构模型选择
弹体材料采用工具钢,夹层结构的面板、背板、肋板材料均使用A3钢,夹层材料为尼龙(聚酰胺-6)。2种金属材料模型均使用Johnson-Cook[10]模型描述本构关系,本构模型方程如下式:
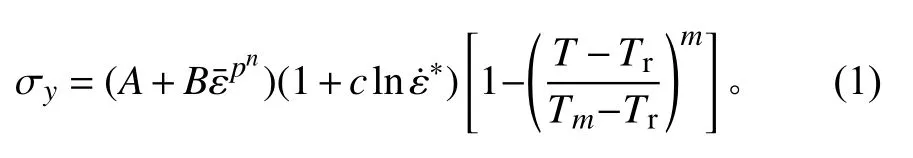
式中:σy为屈服应力;A为静态屈服应力;B为硬化参数;n为硬化指数;C为应变率系数;m为温度软化指数;为等效塑性应变;=为无量纲塑性应变率,T为温度,Tr为室温,Tm为材料熔点。
根据文献[11 - 12]并结合实验得到工具钢和A3钢的材料参数见表1。

表1 工具钢和A3钢的本构与损伤参数Tab. 1 Material constitutive and damage parameters for tool steel and A3 steel
1.2.2 尼龙本构模型选择
通过SPHB实验得到尼龙在不同应变率下的应力应变曲线如图3所示。其屈服强度随应变率的增加而显著提高,表明尼龙是应变率敏感材料。
根据尼龙的实测动态应力应变关系曲线可知,其形态与双线性随动塑形材料模型(Cowper-Symonds[13])吻合度非常高,故本文采用该模型对尼龙的本构方程进行拟合,方程如下式:

图3 尼龙在不同应变率下应力应变曲线Fig. 3 Stress-Strain curve of nylon in different strain rate
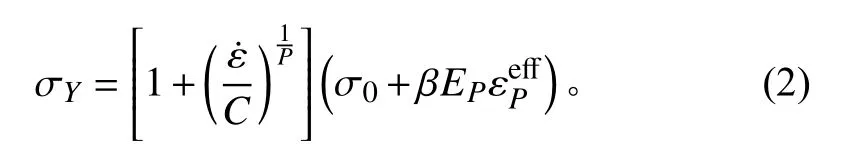
其中:σ0为初始屈服应力;为应变率,C和P为应变率参数;为有效塑性应变;EP为塑性硬化模量。
基于实验数据,通过对尼龙的本构方程拟合得到的相关材料参数见表2。

表2 尼龙的材料参数Tab. 2 Parameters of nylon material
2 数值模型验证
2.1 验证实验方案设计
实验弹体选用工具钢,直径为8.08 mm,质量6.8 g,密度为7.83×103kg/m3,剪切模量为770 MPa,并经过淬火加低温回火热处理后,硬度(HRC)为60,如图4所示。
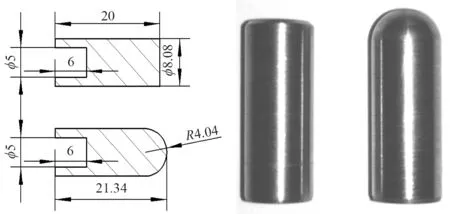
图4 弹体尺寸外形图Fig. 4 The dimension of projectile
实验所使用的炮管内径为25 mm,将弹体装进弹托中,出膛后,弹体和弹托分离,完成实验。钢靶板和尼龙靶板尺寸为200 mm×200 mm,厚度分别为0.84 mm和6.30 mm,四边开圆形孔洞,通过螺栓将靶板与靶板支架连接成一体,如图5所示。
2.2 数值模拟精度分析
2.2.1 钢靶板抗侵彻性能模拟精度对比分析
半圆形弹和平头弹侵彻钢靶板时均产生了冲塞,如图6所示。由钢靶板的应力云图及破口形态可知,平头弹对钢板的破坏形式为剪切破坏,这使得钢板破口处的厚度与钢板本身的厚度几乎相同,破口呈圆帽状且边缘整齐光滑。由图7所示的冲塞形成初期的应力状态及靶板破口形态表明,半圆形弹使钢板产生了拉伸破坏,破口边缘处受拉逐渐变薄直至断裂。观察2种弹头侵彻钢靶板的应力云图与实验产生的破口发现,数值模拟的失效形式与实验高度吻合。

图5 侵彻实验装置示意图Fig. 5 Sketch of experiment set-up

图6 平头弹冲击钢板仿真实验图像对比Fig. 6 Comparison of simulation and experimental images of flat-nosed projectiles impacting steel target plate

图7 半圆形弹冲击钢板仿真实验图像对比Fig. 7 Comparison of simulation and experimental images of hemispherical-nosed projectiles impacting steel target plate
剩余速度是抗侵彻能力的重要参考指标,表3给出了2种弹体侵彻钢靶板的剩余速度的数值模拟和实验结果,误差在±5%左右,精度较高。
2.2.2 尼龙靶板抗侵彻性能模拟精度对比分析
如图8和图9所示,模拟尼龙靶板的破坏形态与实验相吻合,平头弹侵彻尼龙靶板呈剪切破坏,破口处的界面相对光滑;半圆形弹侵彻尼龙靶板时,使尼龙受到的拉应力作用而失效,破口处的界面相对粗糙。2种弹体侵彻钢靶板的剩余速度数值模拟和实验结果见表4,误差同样在±5%左右,具有较好的模拟精度。

表3 弹体垂直侵彻钢板的实验结果对比Tab. 3 Experimental results of vertical penetration of projectile into steel plate

图8 平头弹冲击尼龙仿真实验图像对比Fig. 8 Comparison of simulation and experimental images of flat-nosed projectiles impacting nylon target plate

图9 半圆形弹冲击尼龙仿真实验图像对比Fig. 9 Comparison of simulation and experimental images of hemispherical-nosed projectiles impacting nylon target plate

表4 弹体垂直侵彻尼龙靶板的实验结果对比Tab. 4 Experimental results of vertical penetration of projectile into nylon target plates
通过对钢靶板和尼龙靶板侵彻的数值模拟和实验结果对比,说明采用的仿真模型、材料参数具有较高精度,符合实际情况。
3 夹层结构侵彻响应及性能分析
3.1 肋板角度对抗侵彻性能的影响
弹体接触夹层结构的斜向肋板后,弹体头部受力非对称,从而给予弹体质心一个偏转力矩,造成弹体偏航,增加夹层结构的抗侵彻性能。因此,可将弹体偏角作为夹层结构抗侵彻性能的参考指标。为研究肋板角度对产生偏角大小的影响,采用2种弹体对肋板角度为15°,30°,45°夹层结构进行数值仿真。通过反余弦公式计算弹体剩余速度与剩余速度在竖直方向投映的速度,得到弹体偏角大小。
如图10所示,平头弹侵彻夹层结构时,在相同初速度下肋板角度为15°时的弹体偏角明显大于30°,45°,并且弹体偏角随肋板角度的增大而减小。半圆形弹侵彻夹层结构时,随着肋板角度的增加,弹体的偏角先减小后增加。相同初速度情况下,2种弹体侵彻3种肋板角度的夹层结构,弹体贯穿肋板角度为15°的夹层结构后产生的偏角均为最大。随着弹体初速度的增加,弹体偏角均呈递减趋势,且偏角数值逐渐趋于一致。

图10 弹体初速度与偏角的关系曲线Fig. 10 The curve of the relationship between the initial velocity of the projectile and the deflection angle
3.2 不同弹头形式下夹层结构的响应分析
3.2.1 平头弹侵彻夹层结构
如图11所示,弹体以相同初速度穿透不同肋板角度夹层结构后的剩余速度不同,可知不同倾斜角度的肋板迫使弹体产生偏角,并不同程度地延长弹体在夹层结构内耗能路径。通过弹体的初速度与剩余速度可计算得到弹道极限。平头弹对于肋板角度为15°,30°,45°夹层结构的弹道极限速度分别为820.4 m/s,776.5 m/s和756.0 m/s,即夹层结构抵抗平头弹侵彻的性能与肋板角度的关系为15°>30°>45°。
3.2.2 半圆形弹侵彻夹层结构
不同于平头弹,半圆形弹延性扩孔破坏靶板,穿透过程是一种刺穿性的模式,比平头弹具有更强的侵彻能力。
肋板角度为15°,30°,45°三个工况下,靶板针对半圆形弹的弹道极限速度分别为727.4 m/s,676.2 m/s和683.6 m/s,小于平头弹侵彻夹层结构的弹道极限。如图12所示,半圆形弹侵彻夹层结构肋板角度为15°的靶板时弹体剩余速度与平头弹相同,也明显小于30°和45°的弹体剩余速度,但半圆形弹贯穿肋板角度为45°的夹层结构时的剩余速度小于肋板角度30°的夹层结构。由此可知,对于半圆形弹,肋板角度为15°的夹层结构抗侵彻性能最优,45°次之,30°最弱。

图11 平头弹初速度与剩余速度的关系曲线Fig. 11 The curve of the relationship between the initial velocity of the flat-nosed projectile and residual velocity
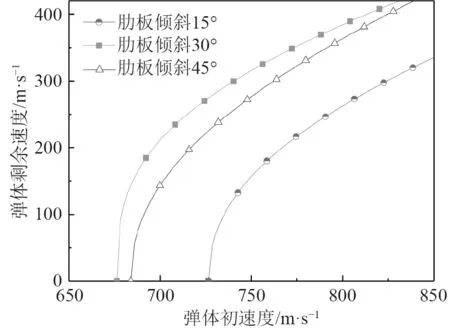
图12 半圆形弹初速度与剩余速度的关系曲线Fig. 12 The curve of the relationship between the initial velocity of the hemispherical-nosed projectile and residual velocity
对比图10~图12,在相同的初速度下,平头弹贯穿不同肋板角度的剩余速度随肋板角度增加而增加,而半圆形弹则先减小后增加。弹体在贯穿不同肋板角度的夹层结构时,弹体偏角的增降趋势与弹体剩余速度的变化趋势相反,即弹体贯穿夹层结构时的偏角与其剩余速度为负相关关系,并且弹体在临界贯穿夹层结构时,产生的偏角最大。
4 结 语
本文对带有3种不同肋板角度的钢/尼龙夹层结构在遭受不同弹头侵彻时的响应情况进行分析,得到以下结论:
1)夹层结构中的斜肋板可以使弹体在侵彻过程中产生偏航,有利于提高夹层结构的抗侵彻性能。
2)弹体在贯穿夹层结构的情况下,弹体偏角随弹体初速度的增加而递减,在贯穿夹层结构的瞬时,弹体偏角达到最大;且弹体贯穿夹层结构时的偏角与其剩余速度呈负相关关系。
3)当肋板角度约为15°时,该夹层结构的抗侵彻性能最优。

