破片撞击下复合夹层板梯度泡沫铝夹芯吸能性能研究

郝高明，陈 震

(上海交通大学 海洋工程国家重点实验室，上海 200240)

0 引 言

多孔泡沫铝是一种既能减轻结构重量，又具有缓冲、吸能、降噪、防火、耐蚀等优良性能的功能性材料[1]，在船舶结构上具有广阔的应用前景。将泡沫铝材料作为夹芯填充到钢质夹层板中，不仅可以减轻结构重量，还可以提高结构的缓冲吸能能力，减轻对船体结构的破坏效果。

当前，国内外对船体泡沫铝夹层板吸能性能的研究基本采用内部孔隙呈均匀随机分布的泡沫铝作为夹芯。但近年来，研究者提出一种密度沿厚度方向存在梯度变化的密度梯度泡沫铝，它兼具优良的能量吸收和极强的可设计性[2]。已有研究结果表明，如能合理地设计密度分布，梯度泡沫铝的冲击吸能性能将会优于均匀随机泡沫铝[3]。因此，密度梯度泡沫铝得到了研究者的普遍关注。

采用数值模拟的方法研究密度梯度泡沫铝的力学性能，基于Voronoi原理，采用Abaqus建立密度呈连续分布的二维Voronoi梯度泡沫铝有限元模型，研究高速破片冲击船体夹层板时，梯度泡沫铝夹芯的变形模式和能量吸收性能，为船舶夹层板芯层结构设计提供参考。

1 数值模型

1.1 模型试验

为验证所采用二维Voronoi模型在力学性能研究方面的可行性，开展泡沫铝准静态压缩试验。试验所用泡沫铝样品尺寸为60 mm×60 mm×100 mm，密度呈均匀随机分布，相对密度ρr（ρr=ρ/ρs，ρ为泡沫铝的密度，ρs为基体材料铝的密度）为0.1。

试验地点为上海交通大学工程力学实验中心，试验仪器采用ZwicK电子万能材料试验机，应变速率为10-4/s。记录载荷-位移数据并计算其对应的应力-应变值，绘制试验应力-应变曲线图。

由于试验样品是三维物体，而模型是二维平面，因此在建模时要考虑维度的影响。根据泡沫铝试样截面特征，定义截面内孔壁面积与截面面积之比为二维模型的相对密度。对泡沫铝试样截面孔隙率进行计算后发现，其对应的二维模型相对密度为0.25。因此，建立相对密度为0.25的二维Voronoi泡沫铝有限元模型，建模时高度还原试样截面特征。

采用Abaqus对试验样件准静态压缩过程进行仿真模拟，铝基材材料的密度为2 700 kg/m3，杨氏模量为70 GPa，泊松比为0.33，屈服应力为70 MPa。应变率与试样试验保持一致。

从图1泡沫铝静态压缩应力-应变曲线实验和模拟结果对比可以看出，试验结果和模拟结果的应力应变曲线数值相近，且应力-应变曲线都是由线弹性阶段、长而平的平台段、密实段3个阶段[4]组成。因此，可以采用二维模型研究泡沫铝的力学性能。

图1 泡沫铝静态压缩应力-应变曲线实验和模拟结果对比Fig. 1 Comparison of experimental and simulated results of static compression stress-strain curve of aluminum foam

1.2 梯度泡沫铝建模

为定量描述梯度泡沫铝，采用线性回归法定义梯度泡沫铝的梯度参数为：

其中：n为模型沿高度方向均分的层数；i为模型各层编号；hi和ρi分别为第i层的高度和相对密度；为各层高度的均值。h方向如图2箭头所示。

图2 梯度泡沫铝二维有限元模型Fig. 2 Two-dimensional finite element model of gradient aluminum foam

根据梯度参数γ符号的差异，可以将梯度泡沫铝分为正梯度泡沫铝（γ>0）、负梯度泡沫铝（γ<0）、均匀随机梯度泡沫铝（γ=0）。γ>0表示梯度泡沫铝密度沿h方向递增，反之为递减。γ=0表示梯度泡沫铝密度呈均匀随机分布。梯度参数γ的绝对值|γ|可反映梯度泡沫铝密度沿h方向变化的快慢。|γ|越大，梯度泡沫铝密度沿h方向变化越快，两端密度差别越大。

根据式（1）规定的梯度参数γ计算式，分别建立了γ分别为0，2.1，1.5，-2.1，-1.5的梯度泡沫铝二维有限元模型，考虑了梯度方向、梯度大小对其力学性能的影响。

1.3 梯度泡沫铝模型的准静态力学性能

对梯度泡沫铝模型进行准静态压缩模拟得到其在应变ε分别为0.2，0.4，0.6，0.8时的泡沫铝压缩变形和应力应变曲线图如图3和图4所示。

由图3所标出的变形圆圈带可以看出，在准静态压缩模式下，梯度泡沫铝的变形带产生于低密度端，并向高密度端逐渐扩展。由Ashby-Gibson公式[5]可得，多孔泡沫铝材料的压缩屈服强度与相对密度ρr1.5成正比。因此，在受到准静态压缩时，梯度泡沫铝的低密度端首先达到屈服应力而屈服。随着屈服区密度渐增，应力也逐渐上升。所以，梯度泡沫铝的应力应变曲线并不像均匀随机泡沫铝那样有应力变化不大的平台段，而是表现为坡度逐渐上升的倾斜直线（见图4），并且，梯度大小|γ|越大，倾斜坡度越大。

图3 梯度泡沫铝模型准静态压缩变形图Fig. 3 Quasi-static compression deformation diagram of gradient aluminum foam model

图4 梯度泡沫铝准静态压缩应力-应变曲线图Fig. 4 Quasi-static compressive stress-strain curve of gradient aluminum foam

2 问题描述

反舰导弹爆炸后产生的破片速度通常可达500～1 000 m/s[6]，虽然破片质量通常只有几克，但高速度使其在几十微秒的冲击时间内具有极大的破坏力。当高速破片冲击夹层板时，夹层板前面板和破片均产生塑性变形，泡沫铝芯层也被压缩产生不可恢复的塑性变形。由于爆炸破片速度较高，通常只是在碰撞处产生局部凹坑或穿透，破坏面积较小，对其他非碰撞处影响较小。

因此，王宇新[7]提出碰撞界面处上面板和破片获得的共同速度vf的方程如下：

其中：ρ材料密度，kg/m3；c为声音在该材料中的传播速度，m/s；ρc为波阻抗，kg/m2s。v为界面处各层材料的初始质点速度。标号1和2分别代表飞片和前面板。

破片材料采用钛合金，其波阻抗ρ1c1为22.6×106kg/m2s。面板材料通常为Q235钢，其波阻抗ρ2c2为40.5×106kg/m2s。将破片速度500～1 000 m/s代入式（3）计算得，碰撞后上面板碰撞处获得的速度vf在179～358 m/s之间。

获得初始速度后，上面板碰撞处开始压缩泡沫铝芯层，受到未碰撞处面板的剪切拉伸力以及泡沫铝芯层的阻力，其速度逐渐衰减至0。在速度衰减过程中，上面板碰撞处受到的阻力[8]也逐渐衰减至0，加速度逐渐下降。因此，可以采用衰减指数函数模拟该速度衰减过程，如下式：

其中：V(t)为t时刻上面板压缩泡沫铝的速度；t为冲击时间；θ为速度衰减时间常数。

对泡沫铝芯层来说，其硬度远低于夹层板面板材料Q235钢。因此，夹层板上下面板均可视为刚体，泡沫铝芯层的压缩过程可以简化为冲击端刚体以指数衰减速度V(t)压缩泡沫铝。

本文主要考虑夹层板在破片冲击下产生局部凹坑时梯度泡沫铝的吸能性能，因此指数衰减冲击过程目标应变设为0.6，即冲击位移为60 mm。冲击刚体速度vf取300 m/s, 经式（S为冲击位移）计算得到，速度衰减时间常数θ为0.2 ms。

图5为冲击端刚体的速度-时间曲线及泡沫铝在冲击 过程中的应变-时间曲线。

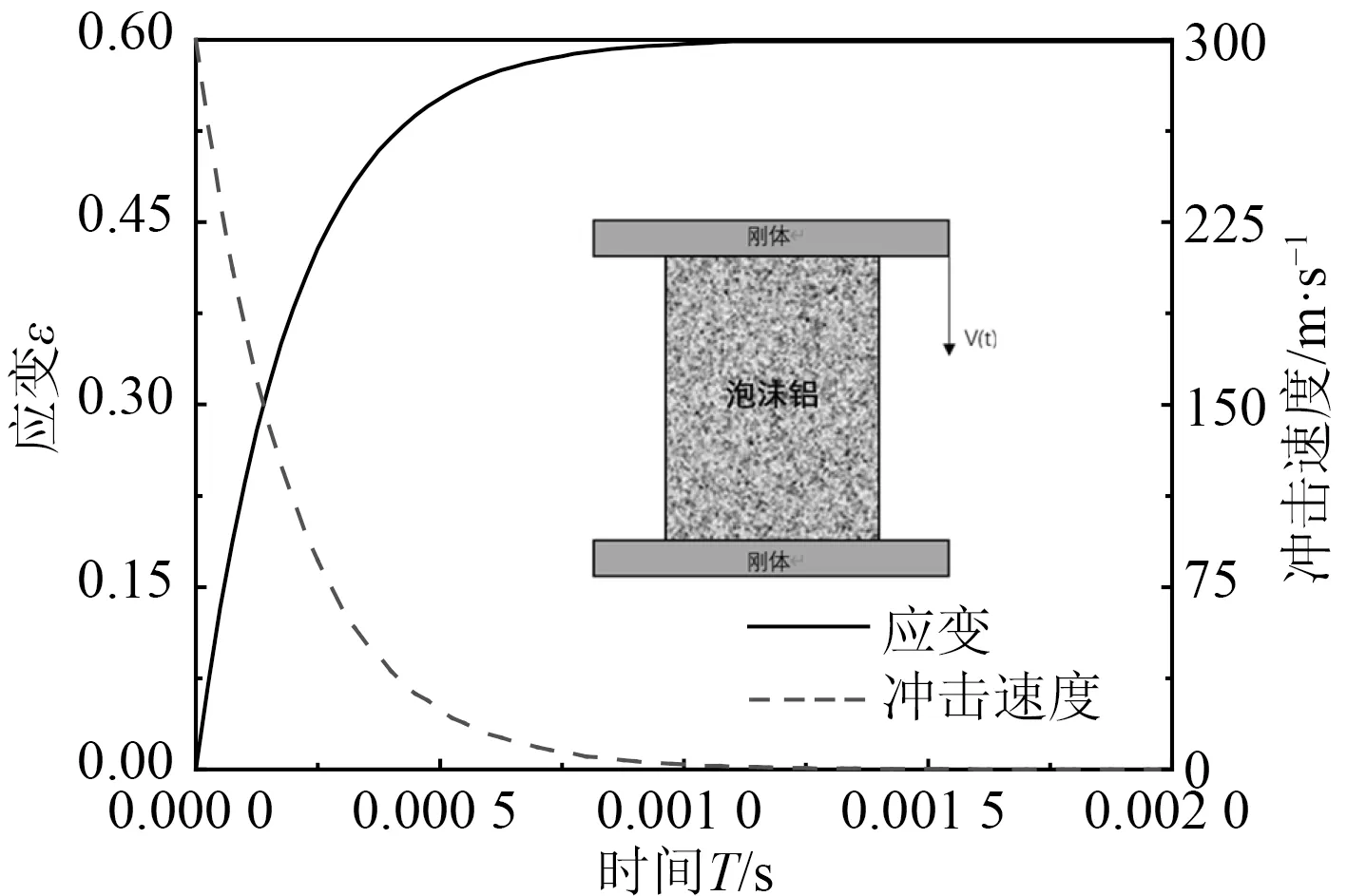
图5 速度-时间曲线和应变-时间曲线Fig. 5 Velocity-time curve and strain-time curve

3 不同类型梯度泡沫铝的变形模式

在准静态压缩模式下，梯度泡沫铝压溃区域产生于低密度端，并向高密度端逐渐扩展。但在指数衰减速度冲击模式下,梯度泡沫铝的变形过程依次为高速冲击段、过渡段、准静态压缩段。本文以梯度参数γ分别为-2.1，0，2.1的梯度泡沫铝为例，分析梯度方向对梯度泡沫铝变形模式的影响。

第1阶段（高速压缩段），梯度泡沫铝靠近冲击端部分的胞孔被逐层压实，且密实程度极高，未压实区域没有出现明显应变，在压实区域与未压实区域之间形成一分界面，如图6所示。

图6 应变为0.2时梯度泡沫铝变形图Fig. 6 Deformation diagram of gradient aluminum foam when the strain is 0.2

第2阶段（过渡段），靠近冲击端的未压实区域继续被压实，但密实程度已有所降低。同时，密度较低的区域开始出现胞壁弯折现象，如图7所示。

图7 应变为0.4时梯度泡沫铝变形图Fig. 7 Deformation diagram of gradient aluminum foam when the strain is 0.4

由于正向梯度泡沫铝低密度端即冲击端，所以在表观上，正向梯度泡沫铝的压溃依旧沿冲击端向支撑端逐渐发展。而负向梯度泡沫铝低密度端为支撑端，所以负梯度泡沫铝除靠近冲击端的孔壁被压溃之外，支撑端区域也出现了明显的胞壁弯折现象。均匀随机梯度泡沫铝则在冲击端外其他区域出现了随机的胞壁弯折。这一阶段，靠近冲击端的未压溃区域仍然贡献了模型整体应变的50%以上，但比例已有所降低，低密度区域贡献的应变逐渐上升。

第3阶段（准静态压缩段），冲击端刚体速度已降低至100 m/s之下，压溃模式变为准静态模式，低密度区域胞壁弯折成为应变产生的主要形式。如图8所示。

图8 应变为0.6时梯度泡沫铝变形图Fig. 8 Deformation diagram of gradient aluminum foam when the strain is 0.6

从最终应变分布情况来看，3种类型梯度泡沫铝60%～70%的总应变由靠近冲击端的上半部分所贡献，如图9所示。由于泡沫铝的吸能能力随相对密度、冲击速度增加而增加[9]，因而不同密度分布的梯度泡沫铝吸能性能必然会有所差异。

图9 γ=0，2.1，-2.1的梯度泡沫铝上下1/2区域应变贡献率曲线Fig. 9 Gradient aluminum foam up and down 1/2 area strain contribution rate curve when γ=0, 2.1, -2.1

4 吸能特性

吸能性能是评估防护结构抗冲击能力的重要指标。冲击端刚体对梯度泡沫铝做的功转化为梯度泡沫铝的动能EK和内能EI，二者之和即为总能量。分析梯度大小、方向对梯度泡沫铝冲击过程中动能、内能变化的影响。

4.1 动能

图10给出了梯度泡沫铝模型在冲击过程中模型总体动能变化图。

由动能公式知，在速度相同的情况下，质量决定物体的动能大小。当受到冲击时，梯度泡沫铝获得动能的区域主要为靠近冲击端的上半部分区域，该区域局部密度的大小决定总体动能的高低。由图10可以看出，在冲击过程中，梯度泡沫铝模型所获动能顺序为：γ-2.1>γ-1.5>γ0>γ1.5>γ2.1，该顺序与各模型靠近冲击端区域密度的顺序相同。负梯度泡沫铝因其“头重脚轻”的密度分布特点获得了更多的动能。另外，在冲击过程中，梯度泡沫铝获得动能后胞壁之间相互碰撞产生塑性变形又将动能转化为内能，因而动能达到极大值后逐渐衰减至0，表现为一凸形抛物线形状（见图10）。

图10 梯度泡沫铝模型的动能曲线图Fig. 10 EK curves of gradient aluminum foam model

4.2 内能

图11给出了梯度泡沫铝模型在冲击过程中的内能吸收曲线图。

图11 梯度泡沫铝模型的内能曲线图Fig. 11 EI curves of gradient aluminum foam model

由图10和图11可知，冲击过程中，梯度泡沫铝所吸收的内能EI与其获得的动能EK呈正比。这是因为在冲击下，梯度泡沫铝内能增加主要是获得动能的冲击端压实层获得速度后，在惯性作用下与未压实界面相互碰撞产生塑性应变从而引起内能增加的结果。因此，梯度泡沫铝模型最终内能的顺序与其在冲击过程中获得动能的顺序相同，即γ-2.1>γ-1.5>γ0>γ1.5>γ2.1。

从最终吸收内能的顺序可以看出，在相同衰减速度冲击模式下，负梯度泡沫铝的吸能能力明显优于随机泡沫铝和正梯度泡沫铝，并且梯度参数绝对值|γ|越大，负梯度泡沫铝的吸能性能越好，正梯度泡沫铝的吸能性能越差。因此，使用负梯度泡沫铝作为船体夹层板芯层，可以大幅提高夹层板的能量吸收能力，从而减小冲击物体对夹层板的毁伤效果，提高夹层板的抗冲击能力。

5 结 语

本文基于Voronoi多边形原理建立二维梯度泡沫铝有限元模型，研究了梯度泡沫铝夹层板受到弹片高速撞击时，梯度大小、方向对梯度泡沫铝夹芯的变形模式和吸能性能的影响，主要研究结论如下：

1）梯度泡沫铝夹芯的变形可分为3个阶段：高速冲击段、过渡段、准静态压缩段。在前2个阶段梯度，泡沫铝塑性变形集中于冲击端。在准静态压缩段，泡沫铝塑性变形集中于低密度段。

2）梯度泡沫铝靠近冲击端区域局部密度越大，获得的动能越大，最终吸收的内能也就越多。梯度泡沫铝最终吸收内能排序为：γ-2.1>γ-1.5>γ0>γ1.5>γ2.1。负梯度泡沫铝的吸能能力明显优于随机泡沫铝和正梯度泡沫铝，并且梯度参数|γ|越大，负梯度泡沫铝吸收的内能越多。