基于干净数据的流形正则化非负矩阵分解

李 华，卢桂馥，余沁茹

（安徽工程大学计算机与信息学院，安徽芜湖 241000）

（∗通信作者电子邮箱luguifu_jsj@163.com）

0 引言

随着信息社会进入大数据时代，高维数据的增长给数据处理带来了极大的挑战，有效的数据表示不但能够提升算法的性能，而且有助于人们发现高维数据背后隐藏的低维本征结构。如何找到原始高维数据的有效低维表示是近年来的一个研究热点［1-4］。很多研究者做了大量的工作来挖掘蕴含在原始数据的内在结构，其中矩阵分解是一种常用的技术。通过矩阵分解算法可以获取高维数据的低秩表示，从而有效地挖掘出蕴含在原始图像数据中的有用信息，使新的数据表示具有更好的识别能力［5-8］。常见的矩阵分解算法有：正交三角分解（QR分解）［9］、非负矩阵分解（Nonnegative Matrix Factorization，NMF）［10-12］等。其中，NMF 是由Lee 等［11］于1999年在《Nature》杂志上提出的，其心理学和生理学的构造依据是对整体的感知是由组成整体的部分感知所构成的，这也恰恰符合人类大脑对事物的直观理解。它基于数据的局部特征提取数据信息，分解之后的矩阵中所有元素都是非负的，是一种有效的图像表示工具。

NMF 自提出之后便得到学者的广泛关注并对其进行了深入的研究。为了提高算法的识别率和有效性，研究人员在NMF 的基础上提出了许多原始NMF 算法的变体，试图从不同的角度对NMF进行改进。Hoyer［13］把稀疏编码和标准NMF算法结合，提出非负稀疏编码（Non-negative Sparse Coding，NSC）算法，使得矩阵分解后系数矩阵的稀疏性较好，这样可以用更少的有用信息来表达原有信息，在一定程度上提高了运算的效率。Zhou 等［14］在图正则化非负矩阵分解（Graph regularized Nonnegative Matrix Factorization，GNMF）算法的基础上为NMF 添加了额外的约束，进一步提出了局部学习正则化NMF（Local Learning regularized NMF，LLNMF）。Wang等［15］提出了一种降维局部约束图优化（Locality Constrained Graph Optimization for Dimensionality Reduction，LC-GODR）算法，将图优化和投影矩阵学习结合到了一个框架中，由于图是预先构造并保持不变的，使得其在降维过程中的图形可以自适应更新。为了能够同时利用数据的全局信息和局部信息来进行图形的学习，Wen 等［16］提出了一种自适应图正则化的低秩表示（Low-Rank Representation with Adaptive Graph Regularization，LRR-AGR）方法。为了同时考虑数据空间和特征空间的流形结构，Meng等［17］提出了一种具有稀疏和正交约束的对偶图正则化非负矩阵分解（Dual-graph regularized Non-negative Matrix Factorization with Sparse and Orthogonal constraints，SODNMF）。万源等［18］提出了一种低秩稀疏图嵌入的半监督特征选择方法（semi-supervised feature selection for Low-Rank Sparse graph Embedding，LRSE），充分利用有标签数据和无标签数据，分别学习其低秩稀疏表示，在目标函数中同时考虑数据降维前后的信息差异和降维过程中的结构信息，通过最小化信息损失函数使数据中的有用信息尽可能地保留下来，从而可以选择出更具判别性的特征。Tian 等［19］提出了一种总方差约束图正则化凸非负矩阵分解（Total Variation constrained Graph-regularized Convex Non-negative Matrix Factorization，TV-GCNMF）算法，将总方差和拉普拉斯图及凸NMF 结合起来，既保留了数据的细节特征，又揭示了数据特征的内在几何结构信息。

为了揭示数据内在的流形数据，考虑到数据所携带的几何信息，Cai 等［20］在标准NMF 的基础上提出了图正则化非负矩阵分解（GNMF）算法，并在实验数据集上获得了较好的实验结果。为了获得原始图像数据集的低秩结构，Li 等［21］提出了图正则化非负低秩矩阵分解（Graph Regularized Nonnegative Low-Rank Matrix Factorization，GNLMF）算法，该算法虽然考虑了利用低秩信息来增强算法的鲁棒性，但其本质上是一种两阶段方法，且由于不能循环迭代，使得其得到的解不是最优的。为了获得数据的局部和全局表示，Lu 等［22］提出了低秩非负分解（Low-Rank Nonnegative Factorization，LRNF）算法。虽然LRNF 的性能较为优异，但它并没有考虑数据的流形结构信息，并且在求解过程中没有明确说明是如何来保证数据非负性的。

研究表明，一方面，原始图像的有效信息常隐藏在数据的低秩结构中，数据通常从嵌入在高维中的低维流形上进行采样；另一方面，在NMF 中添加额外的正则化项可以在一定程度上提高算法抗噪声干扰的能力和算法的鲁棒性。为了解决上述问题，本文提出一种基于干净数据的流形正则化非负矩阵分解（Manifold Regularized Non-negative Matrix Factorization with low-rank constraint based on Clean Data，MRNMF/CD）算法，该算法将含有噪声的原始图像数据进行清洗，使用干净数据进行学习，并且将有效低秩结构和数据的几何信息引入到NMF，使其鲁棒性有了进一步提高。通过在ORL、COIL20 和Yale 三个公开数据集上进行实验，验证了本文MRNMF/CD 算法比现有的其他算法优异。

1 相关工作

1.1 鲁棒性主成分分析（RPCA）

作为最重要的降维方法之一，主成分分析（Principal Component Analysis，PCA）已应用于很多领域。但由于数据中的噪声和异常值，PCA 的性能及应用受到了限制。为了克服PCA 的这些不足，人们提出了鲁棒性PCA（Robust PCA，RPCA）［23-24］用于恢复带有误差的数据原子空间结构［25-26］。

RPCA 假定原始数据为X=(A+E)T∈Rn×m，A∈Rm×n为低秩数据矩阵，E∈Rm×n为添加的噪声误差矩阵。RPCA 的目标是恢复数据的噪声部分，其优化模型为：

其中：α为正参数；‖ · ‖0为矩阵的l0范数。由于模型（1）为非凸的，所以很难得到有效的解。通过将秩函数与l0范数转换为核范数与l1范数，则式（1）转化为下式：

其中：α为正参数，‖ · ‖*表示矩阵的核范数，‖ · ‖1表示矩阵的l1范数。

1.2 图正则化非负矩阵分解（GNMF）

现实世界中，许多数据是嵌入在高维欧氏空间中非线性低维流形上的，然而，NMF 算法和许多改进的NMF 算法在处理原始数据时，没有考虑数据的内蕴几何结构。为了能够发现数据隐藏信息的表示方法，同时又考虑数据内在的几何信息，Cai 等［20］通过将图正则化项融入标准的NMF 框架中，提出了图正则非负矩阵分解算法。该算法假设2 个数据点在原始数据空间中的几何距离如果是邻近，则其在基于新的基向量低维表示中相对应的数据点也应该离得很近。与传统的降维算法相比，流形学习算法能够揭示原始数据内在的几何结构，寻找高维数据在低维空间中的紧致嵌入。GNMF 的目标函数为：

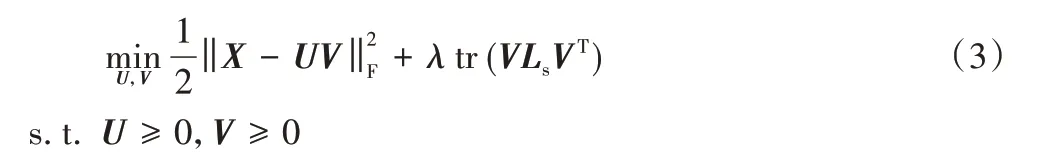
其中：tr(VLsVT)是图正则化项，Ls是图拉普拉斯矩阵，图正则化参数λ＞0。

Cai等在文献［20］中给出了如下的迭代规则：

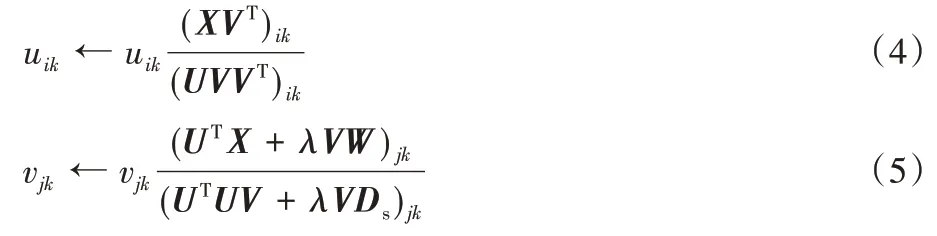
其中：Ds是对角矩阵，W是数据点间的相似度矩阵，Ls=Ds-W。

2 基于干净数据的流形正则化非负矩阵分解

研究表明，使用去噪声的干净数据进行学习有利于恢复数据的原子空间结构，提高算法的鲁棒性和抗干扰能力；并且，原始图像的有效信息常常隐藏在它的低秩结构中，而流形正则化可以保留数据的局部几何结构信息。本文提出的算法，不仅考虑了数据的鲁棒性，使用了去除噪声的干净数据进行低秩非负矩阵分解，而且加入了流形正则化项，从而保留了数据的局部几何结构信息。

2.1 算法模型

给定一个训练集X=[x1，x2，…，xn]∈Rm×n，设E为噪声矩阵，令X=A+E，称A为不含噪声的干净数据。使用训练的干净数据矩阵A进行NMF 分解，将其分为两个非负因子矩阵的乘积，得到：

上式仅学习了局部信息而忽略了数据的低秩信息，于是引入低秩约束，得到：

其中：α＞0，是衡量低秩矩阵A的权值。考虑到此式是NP 难问题，结合RPCA理论，进一步使用下式代替求解：

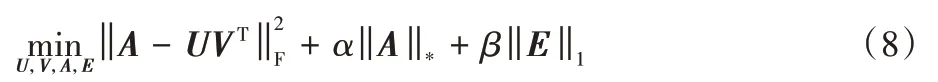
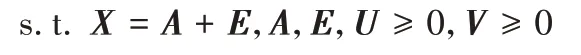
最后，为了利用数据的局部几何结构信息，加入局部图拉普拉斯约束，得到本文算法的最终目标函数：

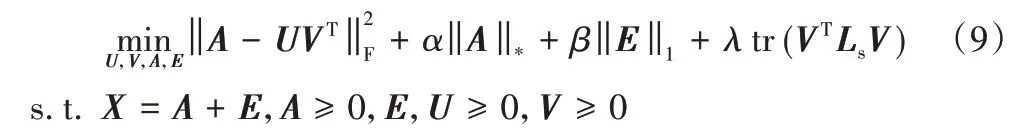
其中权值系数α、β和λ均大于0。目标函数的第一项执行干净数据矩阵A的低秩非负矩阵分解；第二项和第三项表示原始数据经清洗，去掉噪声E，确保用于非负矩阵分解的数据矩阵A是干净的；第四项是图正则化项，保留了图的几何信息。

2.2 模型求解

本节考虑如何对目标函数式（9）进行求解。通过引入辅助变量B，则目标函数式（9）变为：

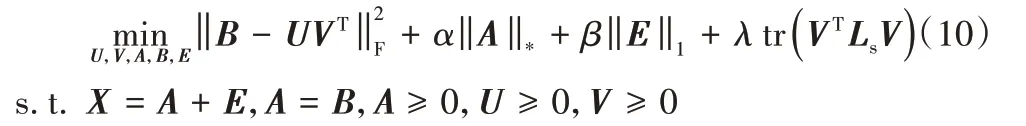
接下来使用增广拉格朗日法对式（10）进行求解，其增广拉格朗日函数为：

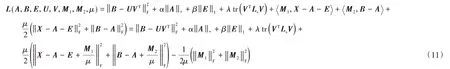
2.2.1 变量A的求解

固定其他变量来计算A，求解式（10）等价于求解：

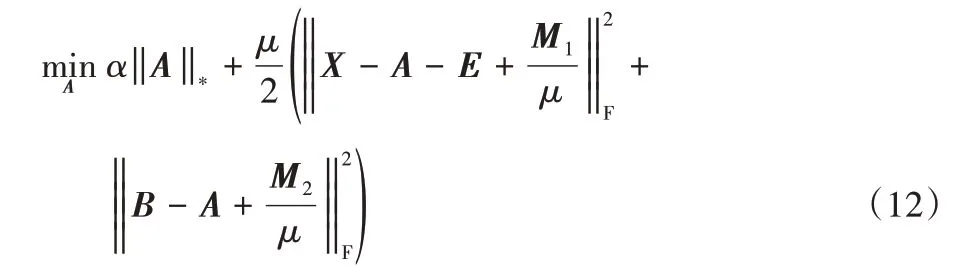
进一步推导，可得：

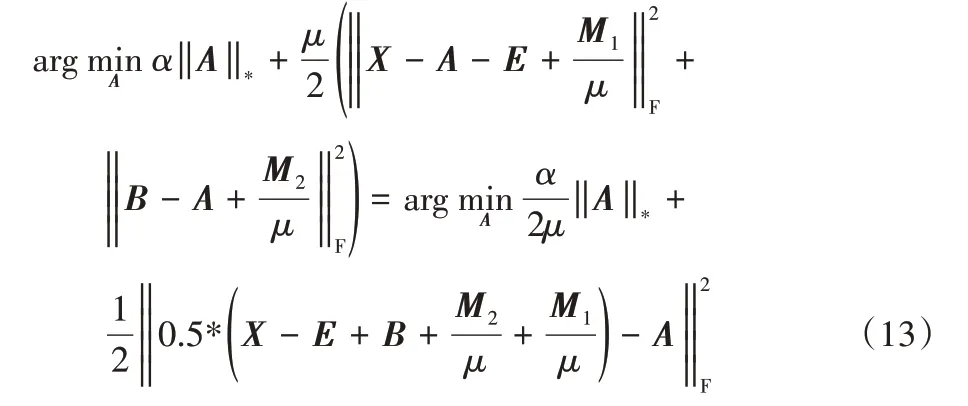
该式可用奇异值阈值法（Singular Value Thresholding，SVT）［27］求解，设的SVD［28］为：

2.2.2 变量E的求解

固定其他变量来计算E，求解式（10）等价于求解下式：

该问题可用shrinkage operator［24］求解。

2.2.3 变量B的求解

固定其他变量来计算B，求解式（10）等价于求解下式：

进一步推导得到：

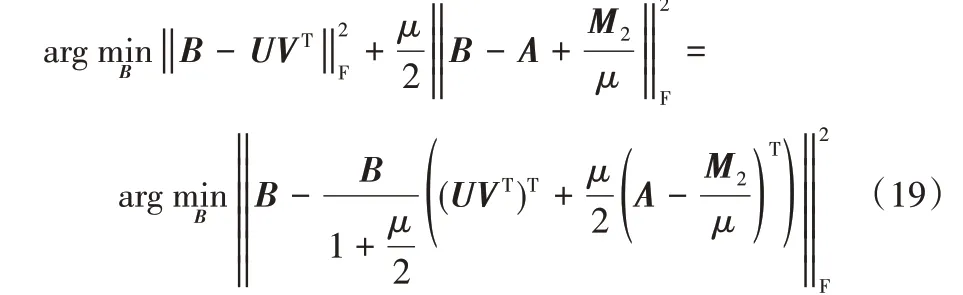
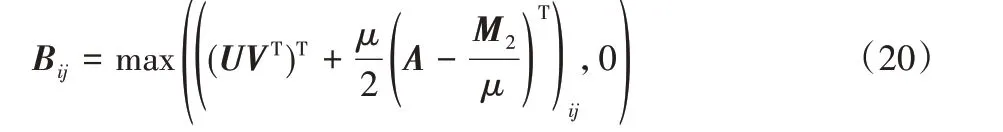
2.2.4 变量U的求解

固定其他变量来计算U，求解式（10）等价于求解下式：

根据矩阵迹的性质，tr(AB)=tr(BA)和tr(A)=tr(AT)，得到：

令φik为约束uik≥0 的拉格朗日乘子，定义Φ=[φik]，则拉格朗日函数L(U)为：

通过式（23）对U求偏导，得到：

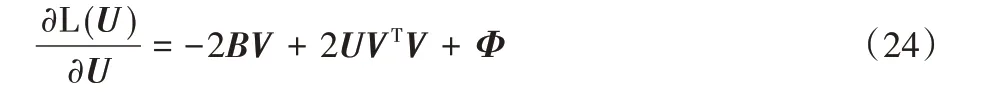
根据Karush-Kuhn-Tuchker（KKT）条件［29］，φikuik=0，得到以下方程：

因此得到uij的更新规则：

2.2.5 变量V的求解

固定其他变量来计算V，求解目标函数式（10）等价于求解下式：

根据矩阵迹的性质，tr(AB)=tr(BA)和tr(A)=tr(AT)，得到：

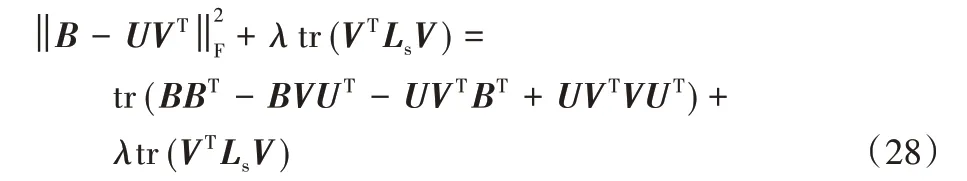
令φjk为约束vjk≥0的拉格朗日乘子，定义Ψ=[φjk]，则拉格朗日函数L(V)为：

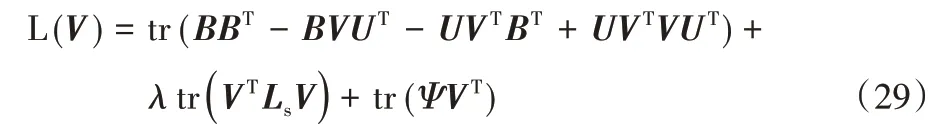
通过式（29）对V求偏导，得到：

根据KKT条件［29］，φjkvjk=0，得到以下方程：

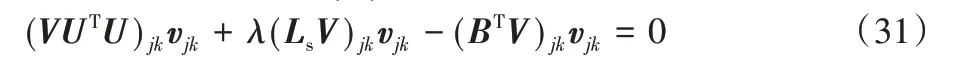
因此得到vjk的更新规则

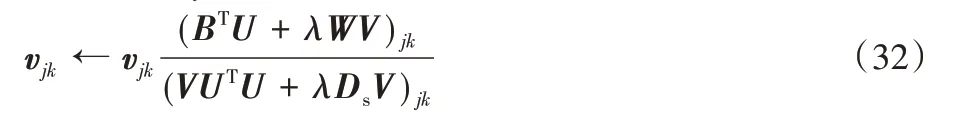
2.2.6 更新变量μ，M1，M2

最后，按照式（33）更新变量μ、M1、M2：

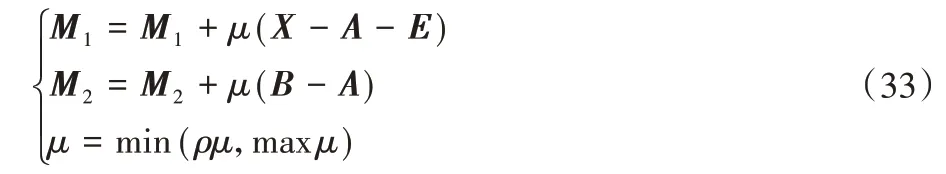
2.3 收敛性分析

本节讨论MRNMF/CD算法的收敛性。

定理1 对于U≥0，V≥0，式（10）中的目标函数值在式（15）、（17）、（20）、（26）、（32）中的更新规则下不增加，因此MRNMF/CD算法收敛。

证明 显然，式（15）、（17）、（20）可分别用第2.2.1 节、2.2.2节和2.2.3节中描述的闭式解来解决。因此，只需要证明式（26）和式（32）在每次迭代中的更新规则下目标值是不增加的。此外，因为式（10）中目标的第二项与U无关，第一项在计算V时不涉及U值的更新，且计算得出V后的操作符合标准NMF，所以MRNMF/CD中的U更新规则与原始NMF完全相同，因此，可以使用NMF 的收敛性证明来证明在等式中更新规则下目标没有增加。有关详细信息，可参考文献［30］。

现在，只需要证明在式（32）中的更新规则下，目标函数不会增加即可。而式（32）中更新规则其实等价于文献［31］中式（26），式（32）的收敛证明可参考文献［31］附录中证明过程，此处不列出。

2.4 时间复杂度分析

本节讨论本文算法的计算复杂度。在算法MRNMF/CD中，第1 步的复杂度为O(mn2)，第2 步的主要步骤的复杂度为O(mn)，第3 步的计算复杂度为O(mnk)，第4 步的计算复杂度为O(mnk)+O(mnk)=O(mnk)，因此算法MRNMF/CD 的总计算复杂度为O(t(mn2+mnk))，其中t为迭代次数。表1 给出了ORL 数据集上NMF、GNMF、MRNMF/CD 算法的实际运行时间。从表1中可以看出，MRNMF/CD 算法复杂度比较高，这主要是因为在MRNMF/CD 算法中，需进行多次SVD，而SVD 的算法复杂度相对较高。这可能会限制应用程序使用具有大量样本的数据。降低算法复杂度的常用方法之一是使用PROPACK进行部分SVD，或者使用文献［32］中的方法，即：

表1 不同算法在ORL数据集上的运行时间对比Tab.1 Running time comparison of different algorithms on ORL dataset

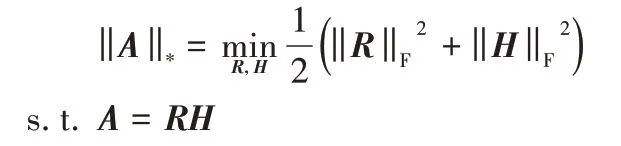
此方法避免了多次SVD，从而降低算法的时间复杂度。在其他数据库中，MRNMF/CD 算法与其他比较方法在运行时间上的差异与ORL数据集类似。

算法 MRNMF/CD。

输入 训练集数据矩阵X∈Rm×n+，参数α、β和λ；

初始化：

B=A，E=0，U=0，V=0，M1=M2=0，μ＞0，λ=0，ρ=0；

迭代：

1）分别使用式（15）、（17）、（20）、（32）、（26）更新A、E、B、V和U；

2）使用下式更新拉格朗日乘子：

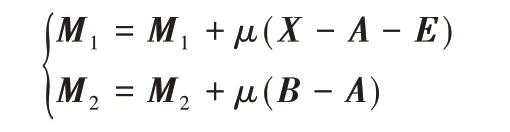
3）更新μ，μ=min(ρμ，maxμ)；

4）t=t+1；

5）得到最优的A、E、B、U、V；

输出 非负矩阵U和V。

3 实验及结果分析

为了评估本文提出的基于干净数据的流形正则化的低秩非负矩阵分解算法MRNMF/CD 的性能，在ORL 人脸数据集、Yale 人脸数据集和COIL20 图像数据集三个图像数据集上进行实验，表2 给出了各数据集及其特征，部分示例图见图1。本文实验条件为11th Gen Intel Core i7-1165G7 @ 2.80 GHz，16 GB DDR3 内存，Matlab2018b。以聚类准确率（ACCuracy，ACC）、标准互信息（Normalized Mutual Information，NMI）两个指标作为参考，实验的对比算法为k-means、PCA、NMF 和GNMF，实验中所用算法的参数已结合原论文根据需要调节至最优。

图1 ORL、Yale和COIL20数据集中的部分图像示例Fig.1 Some examples of images in datasets ORL，Yale and COIL20

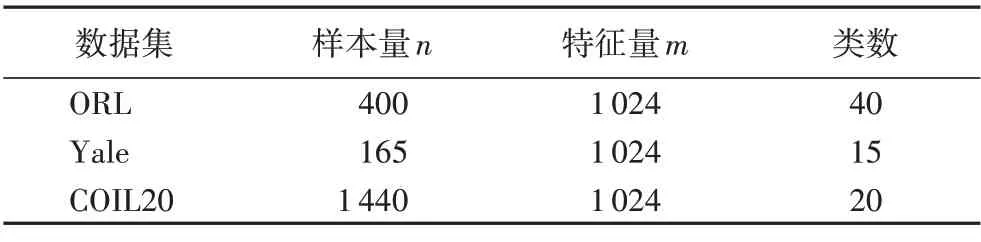
表2 实验数据集及其特征Tab.2 Experimental datasets and their characteristics

在每个数据集上都进行了算法精度测试，每个数据集均进行5 次聚类实验，簇数根据各数据集特征量均匀选取，并对5 次测试取平均值来获得最终的性能得分。对于每个测试，首先应用比较算法中的每个算法，以学习数据的新表示形式，然后在新的表示空间中应用k-means。用不同的初始化将k-means 重复20 次，并记录关于k-means 的目标函数的最佳结果。

3.1 比较算法

对比算法介绍如下：

1）k-means：在原始数据集上进行，不使用样本中包含的任何信息；

2）PCA：能够有效地提取原始数据集中的主要成分；

3）NMF：试图找出2个非负低维矩阵，其乘积近似为原始矩阵；

4）GNMF：试图通过构造一个简单的图来包含数据中的内在几何结构信息；

5）MRNMF/CD：使用去噪声的干净数据进行非负低秩矩阵分解，并且考虑了数据内在几何结构信息，实验中，参数α和β均设为0.1，图正则化参数设置为10。

3.2 图像聚类实验

3.2.1 ORL数据集上的测试

ORL 数据集上的测试结果如表3 所示。可以看出MRNMF/CD 的ACC 和NMI 均值分别为64.61%和77.24%，与GNMF 相比，分别提高了11.91 和19.89 个百分点；与NMF 相比，分别提高了29.01 和39.99 个百分点；与PCA 相比，分别提高了27.61 和38.34 个百分点；与k-means 相比，分别提高了25.11和36.19个百分点。

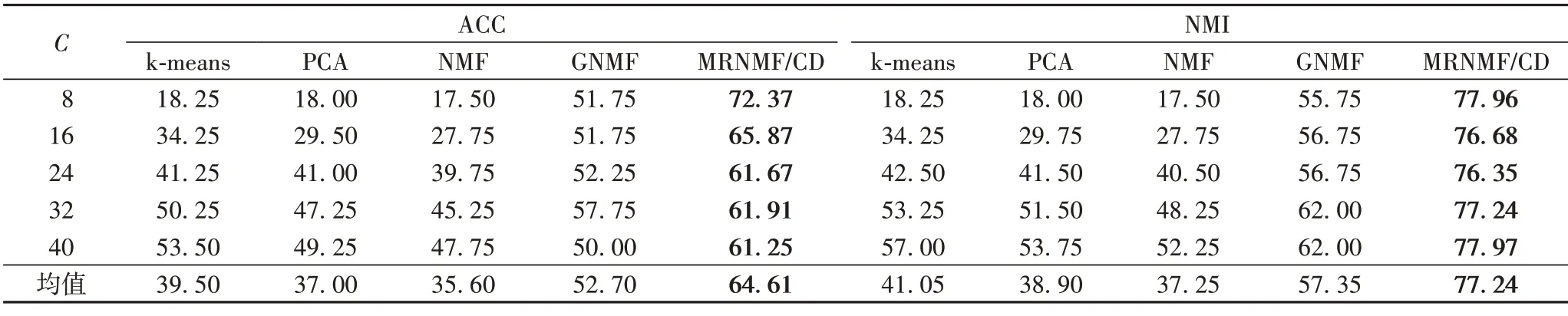
表3 ORL数据集上的聚类结果对比 单位：%Tab.3 Clustering results comparison on ORL dataset unit：%

3.2.2 Yale数据集上的测试

Yale 数据集上的测试结果如表4 所示。可以看出MRNMF/CD 的ACC 和NMI 均值分别为48.90%和42.33%，与GNMF 相比，分别提高了9.14 和1 个百分点；与NMF 相比，分别提高了20.17 和12.63 个百分点；与PCA 相比，分别提高了20.29 和12.87 个百分点；与k-means 相比，分别提高了20.43和13.48个百分点。

表4 Yale数据集上的聚类结果 单位：%Tab.4 Clustering results on Yale dataset unit：%

3.2.3 COIL20数据集上的测试

COIL20 数据集上的测试结果如表5 所示。可以看出MRNMF/CD 的ACC 和NMI 均值分别为59.91%和64.63%，与GNMF相比，分别降低了2.55和0.58个百分点；与NMF相比，分别提高了16.16 和20.34 个百分点；与PCA 相比，分别提高了19.13 和22.67 个百分点；与k-means 相比，分别提高了17.22和20.85个百分点。

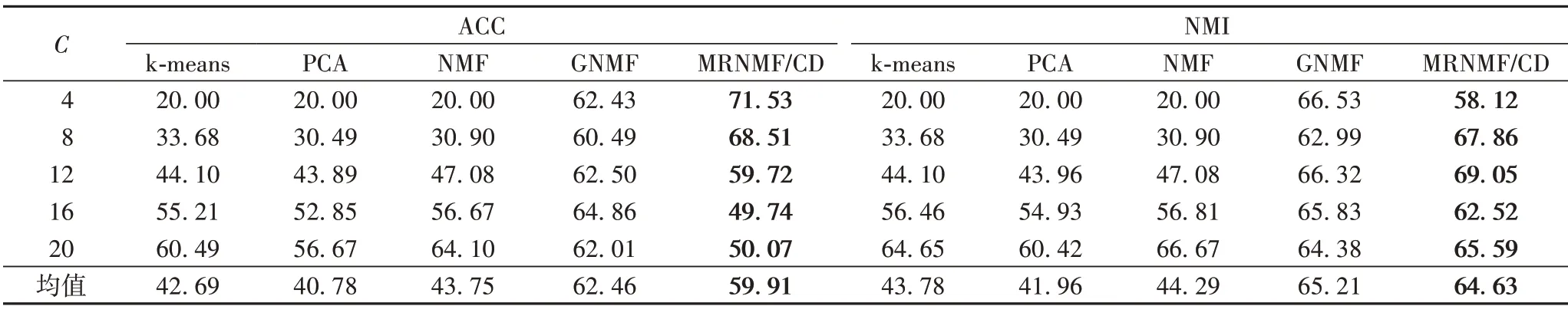
表5 COIL20数据集上的聚类结果 单位：%Tab.5 Clustering results on COIL20 dataset unit：%

3.3 参数选择实验

本节对算法中参数α、β和γ的选择进行讨论，分别在ORL、Yale 和COIL20 三个数据集上测试参数α、β和γ对MRNMF/CD 算法性能的影响。所有实验均使用ACC 指标作为算法评价的标准。为了公平地比较，在每个参数设置下，均会独立重复实验20 次。同时，记录了所有比较方法的最佳平均结果。本节所有方法的迭代次数都根据经验设置为50，聚类的数量设置为等于真实类的数量。在三个数据集上，分别测试参数α、β和γ值在{0.01，0.1，1，10，100}范围的聚类精度变化。实验结果如图2 所示。可以看出，对于参数α，在ORL数据集上当α=1 时可获得较好结果，在Yale 数据集上当α=0.1时可获得较好结果，在COIL20 数据集上当α=1时可获得较好结果；对于参数β，在ORL 数据集上当β=100 时可获得较好结果，在Yale 数据集上当β=0.1 时可获得较好结果，在COIL20 数据集上当β=1 时可获得较好结果；对于参数γ，在ORL 数据集上当γ=0.01 时可获得较好结果，在Yale 数据集上当γ=0.01时可获得较好结果，在COIL20数据集上当γ=1时可获得较好结果。

图2 MRNMF/CD算法中各参数对性能的影响Fig.2 Influence of each parameter on accuracy in MRNMF/CD algorithm

3.4 收敛性研究

本节通过实验验证MRNMF/CD 方法的收敛情况。图3呈现了MRNMF/CD 算法在Yale、COIL20 和ORL 三个数据集上的收敛情况。可以看出，当迭代次数大于35 时，MRNMF/CD算法的目标函数值在Yale 数据集上趋于平稳；当迭代次数大于650 时，MRNMF/CD 算法的目标函数值在COIL20 数据集上趋于平稳；当迭代次数约大于10 时，MRNMF/CD 算法的目标函数值在ORL 数据集上趋于平稳。因此，MRNMF/CD 算法在几个数据集上均收敛，且速度较快。

图3 MRNMF/CD算法在Yale、COIL20和ORL数据集上的收敛曲线Fig.3 Convergence curves of MRNMF/CD algorithm on datasets Yale，COIL20 and ORL

4 结语

本文提出的基于干净数据的流形正则化非负矩阵分解（MRNMF/CD）算法，考虑原始图像数据集噪声干扰和异常值，使用去噪声的干净数据进行矩阵分解，具有一定的鲁棒性，并且在图嵌入和数据重构函数中考虑了有效低秩结构和几何信息，提高了算法的性能。本文还给出了MRNMF/CD 的迭代公式和收敛性证明。最后，MRNMF/CD 在ORL、Yale 和COIL20数据集上的实验表现出比较好的识别率和优越性。