超拓扑空间的超局部紧性

张 敏，王小霞，刘媛媛

(延安大学 数学与计算机科学学院，陕西 延安 716000)

1983年，Mashhour等人去掉了拓扑空间中有限交的条件，在文献[1]中提出了超拓扑空间的定义，将拓扑空间中的连续映射拓展到超拓扑空间中，给出了超拓扑空间中S连续映射、S*连续映射的定义，并给出超Ti(i=1,2)空间的概念，研究了他们的若干性质。2008年，Jassim在文献[2]中提出了超紧空间，并对超紧空间的一些性质进行了研究。AL-shami等在文献[3-5]中引入了超极限点、超闭包算子、超α开集等概念并研究了他们的性质，介绍了超紧(超Lindelöf)、几乎超紧(几乎超Lindelöf)和弱超紧(弱超Lindelöf)、超α紧(超α-Lindelöf)、几乎超α紧(几乎超α-Lindelöf)、超正规等空间的性质及他们之间的关系，并且研究了超R开集和超α开集之间的关系，讨论了超R开集在超R分离公理上的应用。文献[6-8]研究了超拓扑空间中的超可数紧性、超仿紧性、超α-可数紧性的概念及若干性质。

本文在此基础上，主要讨论超拓扑空间中的超局部紧性及其性质，研究了超局部紧空间与超紧空间、超正则空间之间的关系。文中未作其他说明的专业术语均见文献[9]。

1 预备知识

定义1[1]若X上的子集族τ满足：(1)φ,X在τ中；(2)τ中元素的任意并仍然在τ中。则称τ为X上的超拓扑，偶对(X,τ)称为超拓扑空间。τ中的任意一个元素都称为超拓扑空间(X,τ)的超开集，超开集的补集称为超闭集。

定义2[1]设(X,τ)是一个超拓扑空间，x∈X，如果U是X的一个子集，满足条件：存在一个超开集V∈τ使得x∈V⊂U,则称U是点x的一个超邻域。若U是包含着点x的一个超开集，那么他一定是x的一个超邻域，则称U是点x的一个超开邻域。

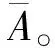
定义4[2]一个超拓扑空间(X,τ)，若对于X的每一个超开覆盖有一个有限超子覆盖，则称超拓扑空间X是超紧空间。

定义5[2]若超拓扑空间X中的任意两个不相同的点x,y，分别存在x,y的两个超开集U,V使得U∩V=φ，则称X为超T2空间。

定义6[3]超拓扑空间(X,τ)中,如果x∈X和A∈X是一个超闭集，使得x∉A，则存在A和x的超开集U,V，使得U∩V=φ，则称X为超正则空间。

定义7[3]设A是超拓扑空间(X,τ)的一个子集，那么包含A的所有超开集的并叫作A的超内部，记作A°。

2 主要结果

定义8 设X是一个超拓扑空间，如果X中的每一个点都有一个超紧致的超邻域，则称超拓扑空间X是一个超局部紧空间。

定理1 超局部紧空间的每一个超闭子空间都是超局部紧的。

证明设X是超局部紧空间，A⊂X，A在X中是闭的，那么A中的任一点x则存在超紧致的超邻域U，所以U∩A为U的超闭子集，并且又因为x∈U∩A，所以U∩A为x在A中超紧致的超邻域，即A是超局部紧的。

定理2 设X1,X2是两个超局部紧空间，则积空间X1×X2也是超局部紧空间。

证明设X1,X2为超局部紧空间，x=(x1,x2)∈X1×X2，那么分别存在x1,x2在X1,X2中的超邻域U1,U2，使U1,U2分别为X1,X2的超紧集，而U1×U2为x的超邻域，并且U1×U2为X1×X2的超紧集，所以X1×X2是超局部紧空间。

定理3 每个超紧空间都是超局部紧空间。

证明设X是超紧空间，x∈X，那么存在x在X中的超邻域U。因为X是一个超紧空间，所以U是超紧集，所以X是超局部紧空间。

定理4 每个超局部紧的超T2空间都是超正则空间。

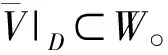
定理5 设X是一个超局部紧的超正则空间，x∈X，则点x的所有超紧的超邻域构成的集族是超拓扑空间X在点x处的超邻域基。

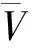
推论1 若X是一个超局部紧的超T2空间，x∈X，则点x的所有超紧的超邻域构成的集族是超拓扑空间X在点x处的超邻域基。

证明设(X,τ)是一个超局部紧的超T2空间，由定理4可知，(X,τ)是一个超正则空间。对任意x∈X，以及x的超开邻域U，都存在x的超紧邻域D，由于D是超紧集，根据定理5，命题得证。

3 结论

本文在超拓扑空间的基础上定义了超局部紧空间，把拓扑空间的一些局部紧性推广到超拓扑空间的超局部紧性上，并给出证明，得到超局部紧空间的每个超闭子空间都是超局部紧的等性质。从而丰富了超拓扑空间的内容。