电力系统中数据-物理融合模型的并联模式性能分析

胡健雄，汤 奕，李 峰，王 琦，赵 璇

（1. 东南大学电气工程学院，江苏省南京市 210096；2. 东南大学数学学院，江苏省南京市 210096）

0 引言

随着交直流混联电网规模的不断扩大，以及新能源等电力电子化设备的大规模并网，现代电力系统呈现出以新能源为主体的新型电力系统发展态势［1-3］，对电力系统分析与运行控制方法提出了更高的要求［4-5］。

由于难以通过实际电力系统试验研究分析电力系统动态特性，通过机理构建物理模型并进行仿真分析成为研究电网特性的重要手段［6-7］。基于详细物理模型的仿真计算，可以在离线状态下对电力系统遭受人为设定扰动后的动态特性进行分析，从而制定电力系统控制策略，但面临着建模困难、计算难度大等问题［8-9］。因此，对于所研究的特定问题，往往通过对研究对象的机理分析，建立具有针对性的物理模型，如功角稳定分析中的扩展等面积准则（extended equal area criterion，EEAC）［10-11］、频率稳定分析中的系统频率响应模型（system frequency response，SFR）［12］等。基于机理分析的物理模型具有机理明确、可解释性好及适应性高的优点，但针对复杂问题也存在建模困难，计算精度与计算效率之间的矛盾等问题［13］。

随着以深度学习为代表的数据科学的快速发展，出现了一批以数据方法为基础的电力系统分析控制方法［14-18］。这类数据方法包括统计分析方法、人工智能方法等，其利用试验或历史数据挖掘数据特征与所研究问题之间的关联关系，避免了对电力系统物理模型的依赖，因此在对复杂场景的分析处理速度上表现出显著优势［14］。如在暂态稳定分析领域，近年来以图神经网络为基础的各类数据方法在分析速度、精度以及对电网拓扑结构变化的适应能力上表现出优异的性能［16］。然而，数据方法虽摆脱了物理模型的限制，但其高度依赖于数据规模和质量，且其结果往往缺乏可解释性［18］，这也制约了其在电力系统领域的大规模实际应用。

对比电力系统物理方法与数据方法，前者基于详细的机理分析，构建电网特征与待研究问题间的因果关系，可解释性高，无历史数据依赖，具有全局性，但难以平衡复杂问题下计算精度与速度间的矛盾；后者基于数据间的关联分析，构建特征与研究问题间的关联关系，计算效率高，可处理复杂问题，但可解释性差，且受限于有限场景下的数据，具有局部性特点。因此，若可以将物理方法与数据方法进行融合，将可以实现两者特点的互补，构建性能更佳的数据-物理融合模型［19］。文献［20］首次提出了数据-物理融合思想在电力系统中的应用，随后融合方法在暂态稳定分析［14，21］、暂态频率分析［15，22］、电力系统模型参数辨识［23-24］等领域均已取得了较好的效果。但现有的数据-物理融合模型的研究往往偏重应用效果，如何将融合模型的构建从定性分析向定量分析提升亟待深入研究。

本文基于电力系统中数据方法与物理方法的特点，总结数据-物理融合模型的构建模式与各自的特点。提出并联模式下物理、数据模型的适用性条件，并在此基础上对并联模式进行理论分析，研究并联模式应用的充分条件，提出融合模型参数的选取方法，确定融合模型泛化误差上限并依据泛化误差上限提出提高融合模型性能的可行性建议，为并联模式下的数据-物理融合模型的构建提供理论支撑。最后，通过并联模式下数据-物理融合模型在暂态功角稳定分析中的应用效果验证了所提假设与分析结论的正确性。

1 基于数据-物理融合的模型构建

1.1 基于数据-物理融合建模的典型模式

电力系统研究中的主要问题一般可以概括为由实际电网采集的状态量等组成的特征域到所研究特定问题的解组成的目标域间的映射f。依据构建电网特征域到目标域间映射f的方法，电力系统问题的研究方法大致可以分为2 类:物理方法与数据方法。

1）物理方法通过对研究对象深层机制和原理的理解来推断其特点，并结合具体应用以合适的表达式描述特征域与目标域间的因果关系，构建电力系统特征x到待研究问题的解y间的映射g:x→y。

2）数据方法避免了对研究对象内部机理的严格分析，其通过大量的测试试验积累反映模型特征的数据，采用不同的数据处理算法，构建特征域与目标域间的关联关系，实现电力系统特征x到待研究问题的解y间的映射h:x→y。

物理方法能够将研究者人为总结的全局知识抽象为具体的机理模型，有助于寻找问题本质和开发新理论；而数据方法通过有限的数据样本，构建相关的经验模型，从数据中挖掘问题的特征。因此，若能够将二者有机结合，综合全局和局部特征、规则与经验，将有助于提出性能更优的联合方法。

数据-物理融合方法的具体联合方式需要结合场景需求进行设计。综合现有研究，指导数据-物理融合应用的主要有并联模式、串行模式、引导模式、反馈模式等4 种融合模式［25］，如图1 所示。

图1 典型数据-物理融合模式Fig.1 Typical data-physical fusion modes

1.2 数据-物理融合模型几种典型模式的特点

1.2.1 并联模式

在电力系统中，由于建模时对部分已知或未知因素的忽略，知识驱动的机理模型与实际对象之间总是存在差异，从而导致机理模型结果的误差难以避免。这种难以用机理模型表达的误差可通过数据驱动的方法进行描述，从而辅助提升机理模型的准确性。并联模式主要适应于物理方法与数据方法均有较好效果的场景，通过将两者结果综合处理后作为最终的输出结果，从而进一步提高模型精度。具体的处理方法包括加权求和、开关函数控制等。

1.2.2 串联模式

电力系统在线业务往往有较高的时效性要求，因而通常采用较简化的物理模型牺牲部分计算精度以满足时效性的要求。电网中大量的可量测特征有利于数据方法的应用，但较大的量测冗余增加了针对特定问题构建经验模型的难度。串联模式通过机理模型高效筛选提取输入特征，进一步采用数据方法可以对机理模型的结果进行直接校正，从而实现数据与知识驱动方法应用的协调。串联模式通过数据驱动的经验模型，修正知识驱动的机理模型的输出结果，从而提高结果准确性。该模式主要适合于简化程度相对较大的机理模型，通过数据方法构建简化机理模型输出结果与实际结果的关联模式，从而校正机理模型结果。

1.2.3 引导模式

传统的数据方法依赖于数据样本中蕴含的关联关系，对于样本数据质量和数量依赖度过高，难以保证生成经验模型的泛化性能。同时，由于数据方法生成的经验模型往往不具备明确的物理意义，缺乏实际指导意义。引导模式以物理方法指导构建合理的数据模型。其基于机理明确的物理模型，指导数据模型的构建与训练，如基于物理机理修改数据方法的训练目标。引导模式适用于希望数据方法结果更符合先验知识的场景，通过修改数据方法设置的方式，将物理模型蕴含的先验知识融入数据模型，从而提高数据方法性能。

1.2.4 反馈模式

电力系统物理模型在构建中往往存在着模块的简化与等效，同时基于离线整定的模型参数往往无法准确反映在线工况下特性的变化。而在实际电力系统运行中，能够依靠各种信息采集设备，对电力系统的状态进行量测。因此，可以通过数据方法调整物理模型中部分模块或主要参数，以提高模型精度。反馈模式适用于物理模型中存在部分机理未知或过于复杂以及参数不确定的场景，其通过数据方法替代或修正物理模型的相关模块或参数，在维持机理模型可解释性的基础上，提高对实际场景的适应能力。

4 种典型融合模式及其应用场景如表1 所示。

表1 典型融合模式及其应用场景Table 1 Typical fusion modes and their application scenarios

通过采用不同融合方法构建数据-物理融合模型，实现二者的有机结合，在各自应用场景表现出更好的性能。但现有的数据-物理融合模型的构建，往往基于定性分析，缺乏定量的理论分析支撑。

本文以并联模式为例，基于对并联模式应用场景的合理假设，提出物理模型与数据模型的适用性条件，并分析并联模式泛化误差，研究并联模式条件，提出融合模型参数的选取方法，确定融合模型泛化误差上限并总结提高模型性能的可行性建议。

1.3 并联模式融合模型定义与适用性条件

1.3.1 并联模式下融合模型定义

假设电力系统n维特征空间中的特征向量x=［x1，x2，…，xn］T∈Rn是满足概率密度函数D0（x）的分布。定义特征向量对应待研究问题的解为y∈R，其由映射f:Rn→R 确定，满足y=f（x）。

基于从D0（x）分布中采样所得的满足D1（x）分布、样本数量为n的数据集T={(x(i)，y(i))|i=1，2，…，n}，数据方法y=h（x）通过在数据集T上训练拟合的映射h:x→y，依赖于数据集T及其分布D1（x）。而基于人为总结机理构建的物理方法y=g（x）则不依赖于采样样本及其分布。

基于物理方法与数据方法，通过不同的融合模式，在分布为D1（x）的数据集T的基础上，将物理方法与数据方法进行融合，从而获得近似于映射f的映射H:x→y。由于融合方法y=H（x）中包含了数据方法，其同样受到数据集T的分布D1（x）的影响。

本文主要分析通过加权求和构建并联融合模式下数据-物理融合模型y=H（x），H（x）定义为:

式中:a∈［0，1］为融合系数。当a取0 时，融合模型H（x）为:

即融合模型退化为纯数据模型。

为方便表述，在不引起歧义的前提下，分别用实际结果y表示实际映射f（x）的输出，g表示物理模型g（x）的输出，h表示数据模型h（x）的输出。

1.3.2 物理模型适用性条件

由于并联模式主要适应于物理方法与数据方法精度较高的场景，则在所融合模型的选择方面，被选用的物理模型本身应具有一定的准确性，采用物理模型输出值g（x）与实际值y=f（x）的相对误差评价物理模型的准确性，对物理模型假设如下:

即物理模型的绝对相对误差小于100%。显然，在满足式（3）的条件下，y与g同号。

1.3.3 数据模型适用性条件

并联融合模式下数据-物理融合模型中的数据模型训练目标可表示为:

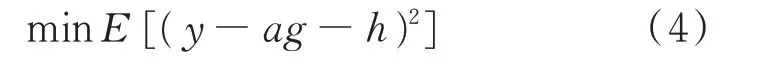
式中:E［·］为求期望函数。

训练完成后数据模型的输出h将受融合系数a的影响，因此h在任意分布D上的期望ED［h］是受a影响较大的函数。设h满足式（5）:

则λ满足式（6）:

分析h/（y-ag），其分母是数据模型h的标签，h为数据模型的输出，其比值λ在D上的期望ED［λ］以及包含λ的函数φ（λ）在D上的期望ED［φ（λ）］主要由所选数据模型的复杂程度与训练效果决定，受a的影响较小。因此，对融合模型中的数据模型做出假设:λ与a无关。

1.3.4 泛化误差定义

基于融合模型的定义以及融合模型中物理模型与数据模型的假设，分别就融合模型与物理模型以及融合模型与数据模型的泛化误差进行比较分析。本文采用平方损失函数计算泛化误差，在忽略采样与传输过程中的误差后，定义融合模型的泛化误差M0为:基于上述假设与定义，下面分别通过融合模型与物理模型、数据模型泛化误差的对比，分析并联模式适用条件，提出融合模型参数的选取方法，并通过推导融合模型泛化误差上限总结提高融合模型性能的措施。

2 融合模型与物理模型误差对比分析

参考式（7）定义的融合模型泛化误差，定义纯物理模型在分布D0（x）下的误差M1为:

定义物理模型系数k（x），同时考虑到对物理模型的假设，有

为表述方便，在不引起歧义的条件下g(x)、y(x)和k(x)简化为g、y和k。将式（9）代入式（8），物理模型误差M1可表示为:

同理，将式（5）与式（9）代入式（7），有

采用做商法比较融合模型误差M0与纯物理模型误差M1，有

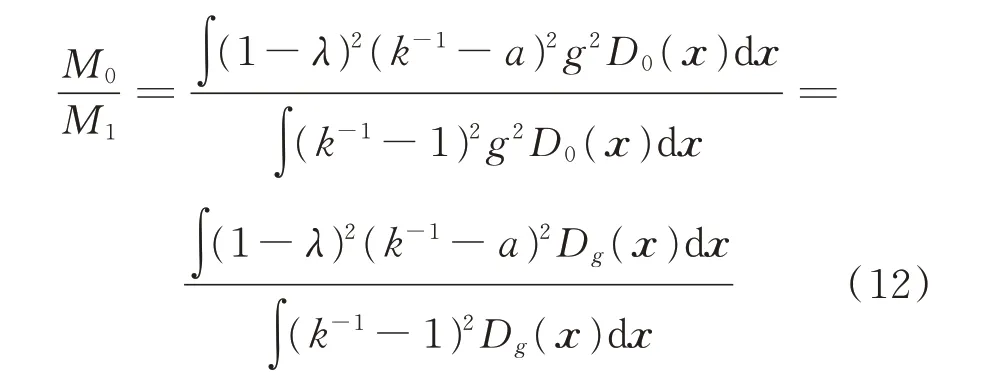
其中，∫g2D0(x)dx为非负常数，概率密度Dg（x）的定义为:

分析式（12）可知:若满足条件k-1∈（0.5，1），总可以取某个融合系数a＜1，使得(k-1-a)2小于(k-1-1)2；若不满足条件k-1∈（0.5，1），则取a=1，保证（k-1-a）2等于（k-1-1）2。

由上述分析可以发现，通过对融合系数a的选取，总能使得（k-1-a）2不大于（k-1-1）2，若在此基础上再满足条件（1-λ）2＜1，则总能保证式（14）成立。进一步考虑式（6）定义以及融合模型中数据模型的相对误差εhr的定义，有

则可得融合模型泛化误差小于纯物理模型的充分不必要条件为:

由式（16）可以看出，融合模型的泛化误差小于纯物理模型的充分不必要条件是融合模型中数据模型的相对误差绝对值|εhr|＜100%。因此，若满足|εhr|＜100%，则融合模型的泛化误差必然小于纯物理模型。

3 融合模型与数据模型误差对比分析

式（1）和式（2）分析了融合模型与纯数据模型的关系，即纯数据模型是融合系数a取0 时的特殊情况。定义纯数据模型泛化误差为M2，有

可见，比较纯数据模型与融合模型的泛化误差等价于分析融合系数a对融合模型泛化误差的影响，即比较融合模型在融合系数a取0 时的泛化误差M0|a=0与a取非0 值时的泛化误差M0|a≠0。经推导变换，M0可变换为如式（18）所示a的函数，具体推导过程见附录A。

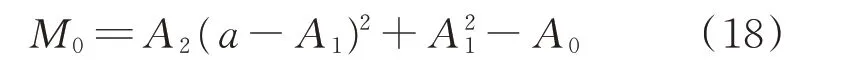
式中:A0、A1和A2的定义见附录A 式（A3）。

由式（18）可以看出，融合模型泛化误差M0是关于a的二次函数，将M0记为M0（a），其开口向上（由于A2＞0），在对称轴a=A1处取极小值。显然，对于泛化误差M0（a），若满足条件A1＞0.5，则必有M0（0）＞M0（a）。对A1进行分析，有

引入类似于式（13）的概率密度变换，并定义概率密度函数Dλg（x）为:

将式（20）代入式（21），则A1可改写为:

由式（9）可知，k-1∈（0.5，+∞），即有:

则融合模型泛化误差M0（a）的极小值点A1∈（0.5，+∞），结合式（18）可知，在融合系数a的定义区间［0，1］上始终有:

即融合模型泛化误差小于纯数据模型。

同时，由于极小值点A1∈（0.5，+∞），则融合系数a取0.5 时，在不知道极值点A1具体取值的情况下，总能保证融合模型精度相较于数据模型具有较大的提升。

进一步分析式（22）可知，M0（a）的极小值点A1是k-1在概率密度函数Dλg（x）下的期望，其中Dλg（x）未知，式（9）对k-1的定义说明k-1是实际结果y与物理模型输出g的比值，虽然对物理模型的假设给出了k-1宽泛的取值区间（0.5，+∞），但依据对一般物理模型的经验，物理模型在大多数情况下误差并不会过大，即k-1应当主要分布在1 附近。

基于上述分析，给出不同融合系数a的取值建议。

1）直接依据对物理模型的经验认识将融合系数a始终设置为1。在融合模型所选用的物理模型性能较好时（即k-1主要分布在1 附近），可以获得效果最佳的融合模型，而在其他情况下，即使不能保证融合模型性能达到最佳，但能保证融合模型优于纯数据模型。

2）利用训练集测试设置融合系数a。在已知训练集上利用式（9）计算并统计k-1的分布，若k-1集中分布于某数a0附近，则设置融合系数a=a0以期获取效果最佳的融合模型（若a0＞1 则取1）；若k-1分布较为分散，则设置融合系数a=0.5，以保证融合模型精度相较于纯数据模型具有较大的提升。

4 融合模型泛化误差上限分析

第2、3 章分别对比分析了融合模型与纯物理模型和纯数据模型的泛化误差。本章分析了融合模型本身的泛化误差，以确定融合模型泛化误差上限并总结提高融合模型性能的可行性建议，为构建高性能并联模式下的数据-物理融合模型提供理论支撑。

参考式（7）所定义融合模型泛化误差，为方便后续表述，此处定义融合模型平方损失函数L（x）为:

则定义基于满足D1（x）分布的训练集S的融合模型训练误差Mtrain为:

再对式（7）所描述融合模型泛化误差进行变换，有

式中:Mtrain在训练中通过优化算法可以达到一个较小的正值。虽然在训练过程中可以采用不同的优化算法，但在训练完成后Mtrain总为一个已知且较小的定值。

通过对式（26）进行推导变换与合理放缩，可构建出不依赖于实际分布（仅依赖于训练和已知的训练集分布）的融合模型泛化误差上限M0max，如式（27）所示，详细的推导过程见附录B。

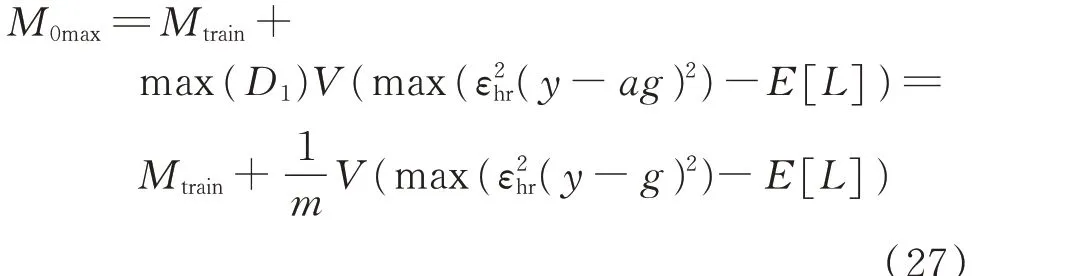
式中:V为特征向量的可行域空间大小。

分析由式（27）所得泛化误差上限可知:

1）训练样本的采样应尽量平均。若采样过于集中，将导致max（D1）增大，即增大融合模型泛化误差上限；相反，采样较为平均可以降低max（D1），从而降低融合模型的泛化误差上限；

2）应尽量将物理模型误差较大的样本纳入训练集。在训练集中的样本通过训练可以有效减少相对误差，通过将物理模型误差较大的样本纳入训练集，降低拥有较大物理模型误差（即（y-g）2较大）的样本的εhr，从而降低max(ε(y-g)2)，有利于融合模型泛化误差上限的降低。

5 算例分析与验证

基于文献［26］中提出的基于数据-物理融合模型的电网暂态临界切除时间（critical clearing time，CCT）在线预测方法，采用本文所提融合模式重新构建针对电网CCT 预测的数据-物理融合模型，并在IEEE 10 机39 节点系统中对所提理论进行测试验证。

5.1 基于并联模式下数据-物理融合模型的CCT预测方法

以集成扩展等面积准则（integrated extended equal area criterion，IEEAC）为代表的EEAC 方法在实际电力系统暂态稳定分析中获得了广泛应用［10-11，26］。该类方法通过互补集群惯性中心和相对运动（complementary-cluster center-of-inertia and relative-motion，CCCOI-RM）变换，将电网暂态轨迹投影到单机无穷大系统上，然后应用等面积准则分析系统稳定性。

为兼顾计算效率，IEEAC 在计算CCT 时通常基于经典的发电机模型，其计算结果存在可能的简化误差。因此，可以采用数据驱动模型来校正这种简化误差，在保证计算效率的同时进一步提高CCT预测精度。本文选择IEEAC 作为CCT 预测的机理模型方法与数据模型根据式（1）进行融合。

在数据模型的选择方面，考虑到极限学习机（ELM）在训练速度以及泛化性能上的优势，本文主要选用ELM 作为融合的数据模型［27］。需要指出的是，数据模型并不限于ELM，也可以选用其他机器学习算法，如k临近算法［28］等。

数据模型不直接使用融合模型的训练集进行训练，而是使用通过式（2）对训练样本的CCT 标签进行处理后的训练集。同时，数据模型的输出值需通过式（1）与物理模型输出的CCT 预测值结合后形成融合模型的CCT 预测值。

5.2 算例设置

采用IEEE 10 机39 节点系统作为测试系统，应用Monte-Carlo 方法生成测试所用样本，其中，Monte-Carlo 方法的参数设置与文献［24］相同，具体设置见附录C 表C1。基于上述方法共生成1 500 组数据用于验证本文理论分析。

基于生成的1 500 组数据样本，构建不同融合系数下的融合模型并在不同样本数训练集下对融合模型进行测试。同时，考虑到本文选用ELM 构建了所测试融合模型中的数据模型，进一步测试了不同融合系数、不同训练集容量的融合模型在不同ELM 隐层节点数下的性能，下文主要对比分析各测试场景下最优ELM 隐层节点的融合模型。融合模型的测试场景的具体参数设置见附录C 表C2。

在评价模型性能时，采用系统受扰后CCT 的实际值与预测值的平均绝对误差（mean absolute error，MAE）和均方根误差（root mean squared error，RMSE）作为具体的评价指标。

依据设计的测试场景与算例设置方法对不同模型进行测试，下面结合实验测试结果分别就不同模型对系统受扰后CCT 的预测效果、本文所提假设以及理论分析结果进行具体分析。

5.3 结果分析

5.3.1 测试结果对比

表2 展示了不同训练集容量下不同融合模型以及物理模型在测试集样本上预测CCT 的MAE 指标、RMSE 指标。其中当融合模型融合系数取0 时，融合模型退化为数据模型。分析测试结果可以发现，融合模型的性能随着训练样本容量的增加而逐渐提升，但随着融合程度（融合系数a）的增加呈现先提升后降低的趋势。在训练集样本数m=1 000，融合系数为0.5 时，融合模型的MAE 指标相较于物理模型提升了41.11%，RMSE 指标相较于物理模型提升了32.50%；相较于物理模型MAE 指标提升了63.32%，RMSE 指标提升了61.15%。

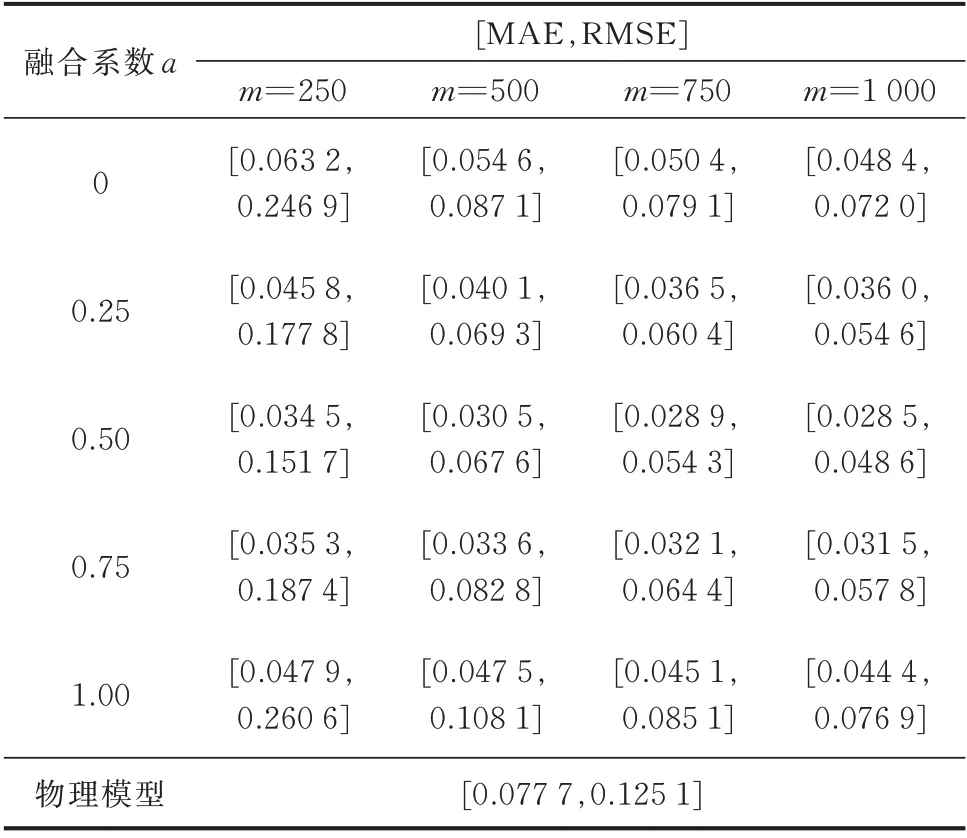
表2 不同训练集下不同融合模型MAE 和RMSE 对比Table 2 Comparison of MAE and RMSE of different fusion models with different training sets

测试结果表明，在训练样本充足时，融合模型性能优于物理模型，而在相同训练集容量下，融合模型优于纯数据模型（a=0 时的融合模型）。但当训练集容量较小时，融合方法的MAE 指标优于物理方法，RMSE 指标普遍低于物理方法，说明在训练样本数量不足时，物理方法具有更好的稳定性。

5.3.2 并联模式适用性条件验证

基于生成样本与上述模型评价方法对所提模型假设进行验证。基于物理模型对全部样本进行测试的相对误差统计结果如图2 所示。

图2 物理模型相对误差统计分布Fig.2 Statistical distribution of relative errors in physical model

由图2 可知，物理模型的相对误差绝对值主要集中于0.25 附近，分布在［0，0.35］内，小于假设中所提出的［0，1］分布范围，满足物理模型假设。

由表3 展示的不同融合系数、不同训练集容量下λ的平均值可知，不同融合系数a下λ均值都接近于1，a对λ影响较小，数据假设成立。图3 展示了全部训练样本的λ统计结果。可见，随着融合系数a逐渐接近于1，式（6）的分母逐渐接近于较小的物理模型误差，使数据模型输出h的波动过度放大，造成了λ分布范围逐渐增大。

图3 λ 的统计分布Fig.3 Statistical distribution of λ

表3 λ 平均值Table 3 Mean value of λ

5.3.3 与物理模型对比

针对本文中提出的融合模型优于物理模型的充分不必要条件，测试并统计训练样本容量为1 000 的条件下，不同融合系数下融合模型中的数据模型相对误差绝对值的分布情况，其统计分布见图4。

图4 数据模型相对误差的统计分布Fig.4 Statistical distribution of relative errors in data model

由图4 可以知道，在a∈［0，0.5］时不同融合模型的数据模型相对误差绝对值主要分布在20%以下，a∈（0.5，1］时相对误差绝对值主要分布在100%以下，均满足式（16）所示的充分不必要条件，融合模型优于纯物理模型，与测试结果相符。其中，在融合系数a接近1 时，会有少量测试样本的数据模型相对误差绝对值超过100%，而测试结果显示此时融合模型同样优于物理模型。造成该现象的主要原因是物理模型的精度较高使得当融合系数取1 时数据模型的输出h的相对误差被过度放大。

5.3.4 融合系数设定分析

由式（18）与式（22）可知，融合模型的最佳性能（即最小泛化误差）由k-1的分布决定。通过式（9）计算并统计k-1的分布情况，结果如图5 所示。

图5 k-1的统计分布Fig.5 Statistical distribution of k-1

由图5 可知，k-1集中分布于0.725 附近，依据式（18）与式（22）可以推测融合模型在融合系数为0.725 附近达到最佳性能。为便于比较，图6 展示了不同训练集及不同融合系数时融合模型的MAE 指标对比。

图6 不同融合模型MAE 对比Fig.6 Comparison of MAE of different fusion models

由图6 可见，融合模型的泛化性能随融合系数a的变化情况与式（18）的二次函数形式基本相符，且在a∈［0.5，0.75］时达到最小值，此时融合模型性能优于a在区间外的性能。此外，a取0.5 时的模型性能优于更接近0.725 的0.75，这是由于k-1的分布并不完全集中于0.75，且式（22）中期望的概率密度分布非平均分布，即融合系数a在0.725 附近时模型性能较好，虽然不能保证融合系数a在0.725 时式（22）取最小值，但依据文中分析取融合系数为0.75 时，融合模型仍能取得较好性能。

6 结语

本文针对数据-物理融合方法理论研究问题，总结了数据-物理融合模型构建模式与各自的特点。针对并联模式提出了合理假设，研究了并联模式适用条件与融合参数的选取方法，并进一步确定了融合模型泛化误差上限，提出了降低泛化误差上限的可行性建议，为并联模式下的数据-物理融合模型的构建提供了理论支撑。通过在电力系统暂态功角稳定分析中的应用验证了所提假设与分析结论的正确性。

并联模式主要适应于物理方法与数据方法效果较好的场景，根据应用场景不同，还有串联模式、引导模式和反馈模式需要详细的理论分析，有待于进一步研究以完善数据-物理融合方法的应用。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。