二维自相似变换理论和线怪波激发*

张解放 俞定国 金美贞

1)(浙江传媒学院智能媒体技术研究院,杭州 310018)

2)(浙江省影视媒体技术研究重点实验室,杭州 310018)

3)(浙江传媒学院媒体工程学院,杭州 310018)

4)(浙江传媒学院网络数据中心,杭州 310018)

我们提出了二维自相似变换理论,以聚焦的(2+1)维NLS 方程(数学称为抛物型的非线性微分方程)为模型,构建了它被转变为聚焦的(1+1)维NLS 方程的二维自相似变换,深入研究了它的空间怪波激发,发现除了(1+1)维NLS 方程的Peregrine 孤子、高阶怪波和多怪波诱导的线怪波所具有的短寿命特征外,由Akhmediev 呼吸子(AB)和Kuznetsov-Ma 孤子(KMS)诱导的线怪波也具有这种短寿命特征.这与由亮孤子(包括多孤子)诱导的空间相干结构保持形状和幅值不变的演化特征完全不同.通过图示展现了本文例举的各类线怪波的演化规律.本文揭示的线怪波激发新机制,有助于提升对高维非线性波动模型的相干结构的新认识.

1 引言

怪波是一种典型的自然现象,可以出现在多种不同的环境中,研究领域包括流体力学[1-3]、非线性光学系统[4,5]、等离子体[6,7]、玻色-爱因斯坦凝聚[8,9]、湍流[10]、微波[11]、超流体[12]、大气[13]、通讯[14]、毛细管系统[15]、金融系统[16]、颗粒物质[17]和磁性材料[18].怪波,源于海洋的粗糙背景下的局部大海浪而得名,具有大波幅、高陡峭、无预兆、短寿命等显著特征,是一种能量高度集中的灾难性波浪,已有大量的实测报道[19,20],严重威胁船舶的航行安全和海洋结构物的运作稳定.

Peregrine 在(1+1)维(one spatial dimensions and one temporal dimension)非线性薛定谔方程(1DNLSE)中首先发现一种时空双重局域的新型Peregrine 孤子(PS)[21],验证了“来无影去无踪”特征,因此将PS 作为怪波的原型成为共识,自然将1DNLSE 作为产生怪波的一个理想模型.Akhmediev教授等指出1DNLSE 的怪波是一种非奇异的有理形式解,是Akhmediev 呼吸子(AB)[22]和Kuznetsov-Ma 孤子(KMS)[23,24]的极限情形,并相继发现了NLS 方程的高阶怪波和多怪波解[25-31].

怪波的奇异特征、独特物理机制和有价值应用背景,一直是学术界的研究热点.尽管在开放的海洋中怪波是危险和不受欢迎的,但在光学中却是有用的,为产生峰值能量集中的强大超短脉冲开辟了途径.近20年来,关于怪波的研究既有丰富的理论成果[32-41],又有不断丰富的实验验证[42-48].值得指出,对二维空间怪波的认识和表征相比较一维空间怪波似乎少的多,因此寻求二维空间的非线性演化模型的怪波激发仍然引起学者的强力兴趣.最近我们建立一种自相似变换方法,得到了非自治KP 方程有理函数表示的二维单、双、三怪波解[49]和Fokas 系统的二维怪波激发[50].本文进一步发展自相似变换理论,以(2+1)维NLS方程[51]为模型,构建了它的二维自相似变换,深入研究了它的线怪波激发,发现由AB 和KMS 诱导的空间相干结构与PS 诱导的空间一样相干结构是线怪波,具有短寿命特征.而由孤子(包括多孤子)诱导的空间相干结构是线孤子,保持形状和幅值不变.

2 二维自相似变换理论

(2+1)维(two spatial dimensions and one temporal dimension)NLS 方程(2DNLSE)具有如下无量纲形式[52]

其中α,β和γ是实常数,ψ=ψ(x,y,t)是复函数.如果α＞0,2DNLSE(1)在x方向被说为聚焦的或吸引的;如果α＜0时,2DNLSE(1)在x方向被被说为散焦的或排斥的.类似地,β的符号导致在y方向是聚焦或散聚焦的.如果αβ ＜0,2DNLSE(1)称为双曲型方程;如果αβ ＞0,2DNLSE(1)称为椭圆型方程.椭圆型2DNLSE(1)可以作为描述模拟光脉冲在光纤中[53]的传播、等离子体[54]中的Langmuir 波以及玻色-爱因斯坦凝聚[55,56]等模型;双曲型2DNLSE 可以作为描述深水中的重力波[57]、等离子体中的回旋波[58]和平面波导中的光波等模型[59,60].

为了研究方程(1)的怪波解,我们引入了下列相似变换[61]

其 中ρ(t),ϕ(ξ,τ),φ(x,y,t)和ξ=ξ(x,y,t),τ=τ(t)分别是指定变量的待定函数.将(2)式代入方程(1)导出

若ρ(t),ξ(x,y,t),τ(t),φ(x,y,t)满足下列关系

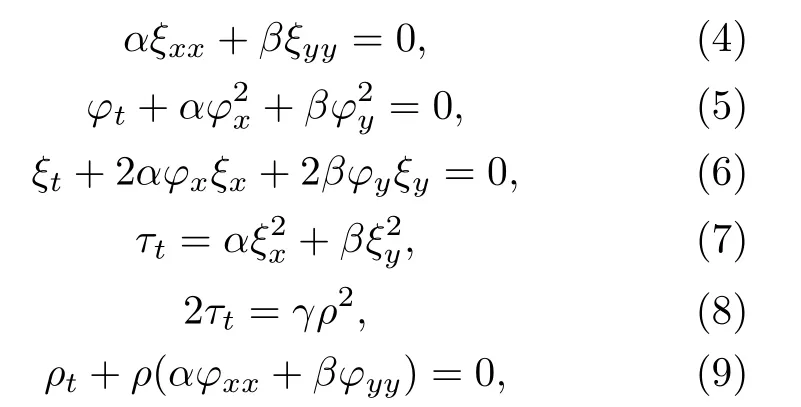
那么(3)式就可转化为标准的(1+1)维非线性薛定谔方程

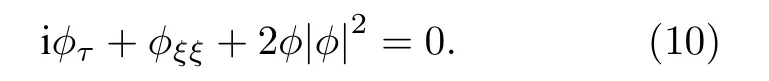
从(4)式和(5)式可假定相似变量ξ(x,y,t)和φ(x,y,t)具有如下形式:

其中κ(t),ι(t),ω(t),a1(t),a2(t),b1(t),b2(t),c(t),都是变量t的待定实函数.考虑到 (11)式和(12)式,从(5)式和(6)式可以求得

由(8)式和(9)式,我们分别得到

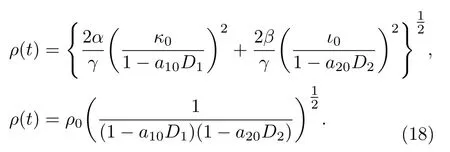
考虑到ρ0是一个常数,要求(18)式成立,存在以下两类情况.

(i)当α=β=λ时,则可得到

值得说明,我们之所以把方程(1)通过自相似变换转化到方程(10),在于方程(10)已有诸多的解析解研究成果,诸如行波解、亮孤子解、暗孤子解、呼吸子解和有理数解等.下面我们主要研究空间怪波激发,并限定讨论α,β,γ符号相同的情形.

3 线怪波激发

这里我们直接基于已知(1+1)维NLS 方程(10)的相关相干局域结构,讨论(2+1)维NLS方程(1)线怪波激发.考虑到(19)—(22)式比(23)—(26)式更有一般性.本节我们仅讨论带有(19)—(22)式的自相似变换(2)式下的情形,并取ξ0=τ0=φ0=0.

3.1 PS 诱导的线怪波

文献[62]中,已知(1+1)维NLS 方程(10)的有理多项式解φ(ξ,τ)具有如下基本形式:

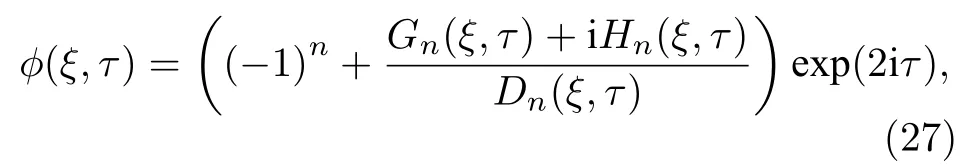
其中n∈N表示解的阶数.不同阶的怪波具有不同的Gn(ξ,τ),Hn(ξ,τ),Dn(ξ,τ),越高阶的怪波,有理多项式的形式更复杂.

基于自相似变换(2)和(19)—(22)式和(1+1)维NLS 方程(10)的一阶怪波[62],即PS,我们导出(2+1)维NLS 方程(1)的一阶线怪波

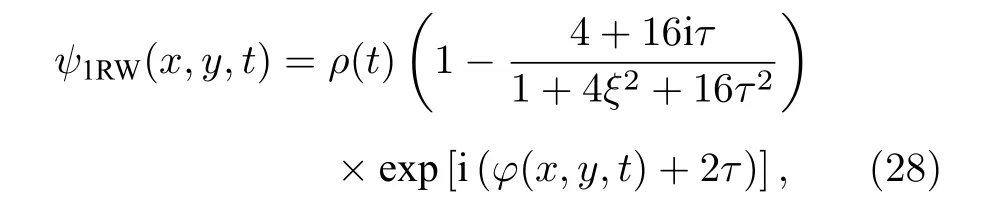
其 中ξ(x,y,t),τ(t),φ(x,y,t),ρ(t)由(19)—(22)式给出.

图1 展示了(2+1)维NLS 方程(1)的一阶线怪波(2)随传播变量t的演化图,图中的自由参数选为λ=1,γ=2,κ0=ι0=-a0=b0=1.可见,一阶线怪波在 (x,y)-平面上呈现出类似线孤子,可称为线怪波,但与线孤子不同,它大振幅、短寿命显著特征.

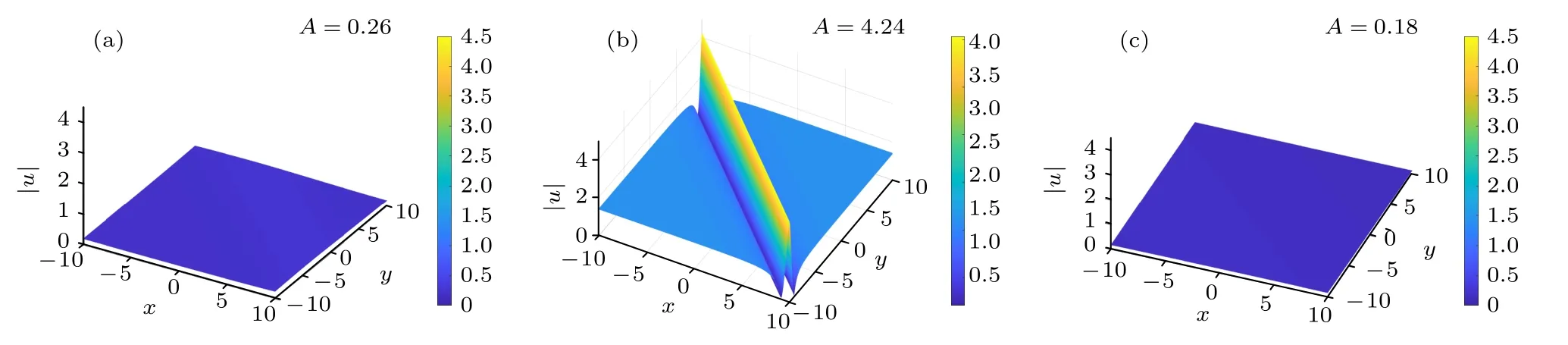
图1 一阶单线怪波(28)在 (x,y) -平面上随t 的演化图:(a) t=-3 ;(b) t=0 ;(c) t=5,自由参数选取为 α=β=λ=1,γ=2,κ0=ι0=-a0=b0=1Fig.1.Evolution plots of the first-order single line-rogue wave (28)with the t on the (x,y) -plane.(a) t=-3 ;(b) t=0 ;(c) t=5.The free parameters are chosen as α=β=1, γ=2,κ0=ι0=-a0=b0=1.

3.2 二阶怪波诱导的线怪波

基于自相似变换(2)与(19)—(22)式和(1+1)维NLS 方程(10)的二阶怪波[28],我们导出(2+1)维NLS 方程(1)的二阶线怪波

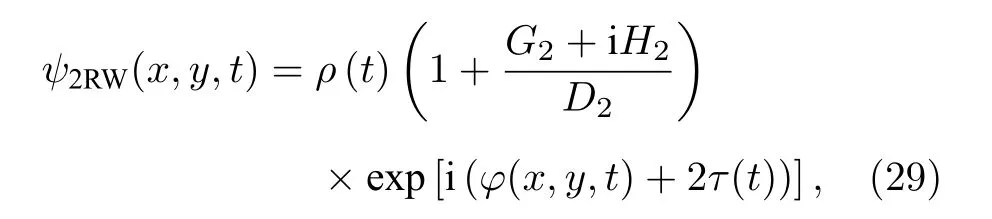
表达式中G2,H2,D2分别为:

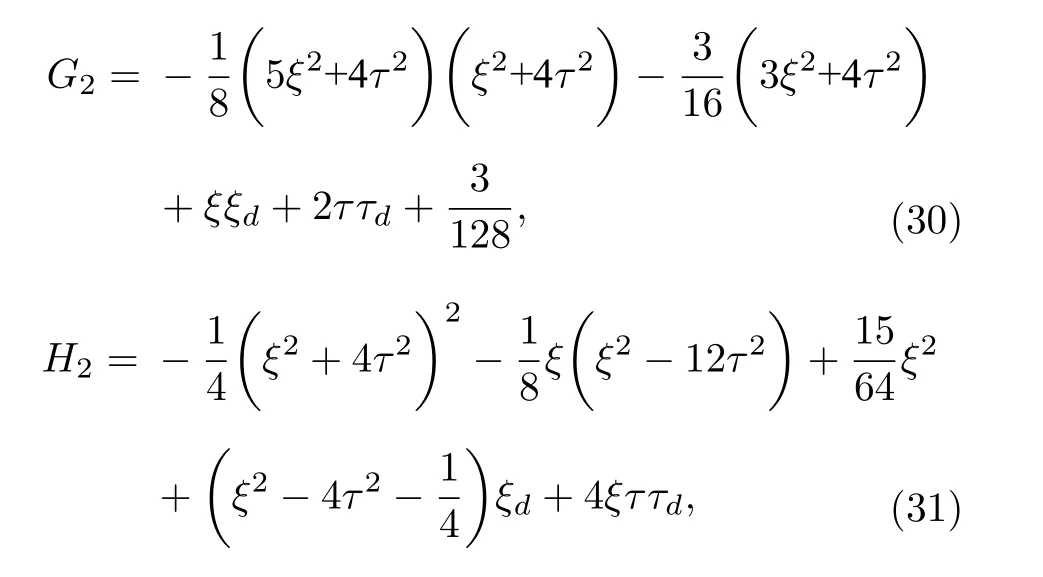
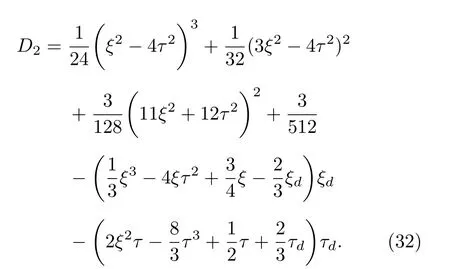
其中ξ,τ,φ,ρ由(19)—(22)式给出.

图2 展示了(2+1)维NLS 方程(1)的二阶线怪波解(29)随传播变量t的演化图,自由参数选为自由参数选取为α=β=λ=1,γ=2,κ0=ι0=-a0=b0=1,ξd=τd=0.从图2 可见,二阶线怪波和一阶线怪波的特征也类似,但幅值更大、局域性更强.至于(2+1)维NLS 方程(10)的更高阶怪波,可以同理讨论,限于篇幅从略.

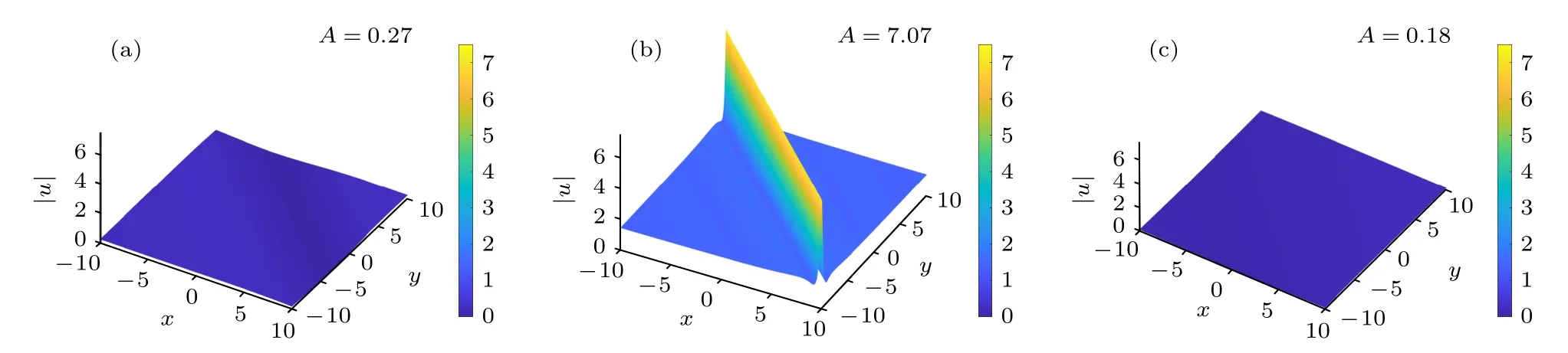
图2 二阶单线怪波(29)在 (x,y) -平面上随 t 的演化图:(a) t=-3 ;(b) t=0 ;(c) t=5,自由参数选取为α=β=λ=1,γ=2,κ0=ι0=-a0=b0=1,ξd=τd=0Fig.2.Evolution plots of the second-order single line-rogue wave (29)with the t on the (x,y) -plane.(a) t=-3 ;(b) t=0 ;(c) t=5.The free parameters are chosen as α=β=1, γ=2,κ0=ι0=-a0=b0=1,ξd=τd=0.

3.3 怪波簇诱导的多线怪波

我们知道怪波簇(rogue wave cluster)是(1+1)维NLS 方程(10)的一些特殊高阶怪波.其本质是高阶怪波可以分解为一系列低阶PS.这些低阶PS 在 (ξ,τ)-平面上相互联系并相互作用,形成各种各样的怪波簇结构,譬如著名的怪波三连体、环形怪波簇和三角怪波级联等,已有很多关于怪波簇的文献[29,62-64]研究.这里我们仅讨论最简单的怪波簇类,即三PS 怪波簇诱导二线怪波.它们可由选取二级线怪波(29)中的自由参数ξd,τd不同时为零得到.为了更清楚的呈现相关特征,我们分别将G2,H2,D2替换为A2,B2,C2[62]

(29)式变为

其中ξ,τ,φ,ρ由(19)—(22)式给出,δ,µ自由参数.

图3 展示了(2+1)维NLS 方程(1)的双怪波(37)随t的演化图,自由参数选为自由参数选取为α=β=λ=1,γ=2,κ0=ι0=-a0=b0=1,δ=25,µ=100.从图3 可见,二阶单线怪波转化为双线怪波.至于(2+1)维NLS 方程(10)的其他形态的怪波簇诱导的多线怪波,可以类似讨论,限于篇幅从略.

图3 双线怪 波(37)在 (x,y) -平面上随 t 的演化图:(a) t=-3 ;(b) t=0 ;(c) t=5,自由参数选取为α=β=λ=1,γ=2,κ0=ι0=-a0=b0=1,δ=25,µ=100Fig.3.Evolution plots of the double line-rogue wave (37)with t on the (x,y) -plane.(a) t=-3 ;(b) t=0 ;(c) t=5.The free parameters are chosen as α=β=1, γ=2,κ0=ι0=-a0=b0=1,δ=25,µ=100.

3.4 AB 诱导的多线怪波

基于相似变换(2)与(19)—(22)式和(1+1)维NLS 方程(10)的Akhmediev 呼吸子解[65],可以导出(2+1)维NLS 方程(1)的多线怪波

其中ξ,τ,φ,ρ由(19)—(22)式给出,a＜0.5是一个正的参数,B=[8a(1-2a)]1/2,ω=2(1-2a)1/2.

图4 展示了由(1+1)维NLS 方程(1)Akhmediev 呼吸子诱导(2+1)维NLS 方程(1)的多线怪波随变量t的演化图,图中的自由参数选为自由参数选取为α=β=λ=1,γ=2,κ0=ι0=-a0=b0=1,a=0.45.这种情况下,参数a决定多线怪波的数目,随a取值趋近 1/2,就转变成一阶单线怪波.

图4 多线怪波(38)在 (x,y) -平面上随 t 的演化图:(a) t=-3 ;(b) t=0 ;(c) t=5,自由参数选取为α=β=λ=1,γ=2,κ0=ι0=-a0=b0=1,a=0.45Fig.4.Evolution plots of the multi-line rogue wave (38)with t on the (x,y) -plane.(a) t=-3 ;(b) t=0 ;(c) t=5.The free parameters are chosen as α=β=1, γ=2,κ0=ι0=-a0=b0=1,a=0.45.

3.5 KMS 诱导的单线怪波

基于相似变换(2)与(19)—(22)式和(1+1)维NLS 方程(10)的Kuzenetov-Ma 孤子解[65],可以导出(2+1)维NLS 方程(1)的单线怪波其中ξ,τ,φ,ρ由(19)—(22)式给出,1 ≥a ＞0.5是一个正的参数,A=i[8a(2a-1)]1/2,Ω=2i(2a-1)1/2.

图5 展示了由(1+1)维NLS 方程(10)的Kuzenetov-Ma 孤子诱导的(2+1)维NLS 方程(1)的单线怪波在x-y平面上的演化图,自由参数选为α=β=1,γ=2,κ0=-a0=b0=1,a=0.8.这种情况下自由参数a的取值不影响单线怪波的形态,但对线怪波的幅值有影响.

图5 线怪波(39)在 (x,y) -平面上随 t 的演化图 (a) t=-3,(b) t=0,(c) t=5,自由参数选取为α=β=λ=1, γ=2,κ0=ι0=-a0=b0=1,a=0.45Fig.5.Evolution plots of the line rogue waves (39)with t on the (x,y) -plane.(a) t=-3 ;(b) t=0 ;(c) t=5.The free parameters are chosen as α=β=1, γ=2,κ0=ι0=-a0=b0=1,a=0.45.

4 讨论和结语

为了比较,基于(1+1)维NLS 方程(10)的单亮孤子和自相似变换(2)式及(19)—(22)式,我们给出(2+1)维NLS 方程(1)的单线孤子

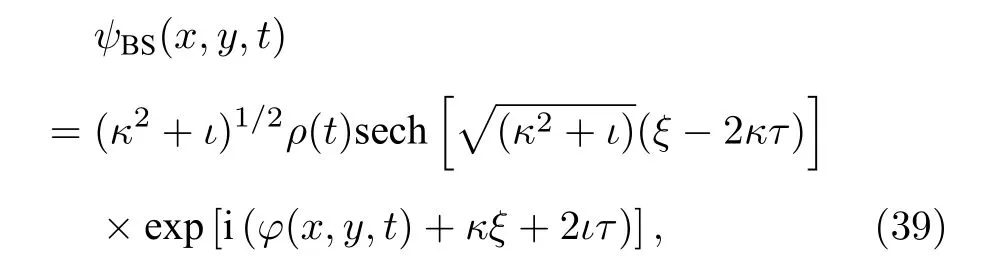
其中ξ,τ,φ,ρ由(19)—(22)式给出,κ,ι是自由参数.可以发现(1+1)维NLS 方程的亮孤子(40)诱导的线孤子具有保持形状和幅值不变的演化特征(图形讨论从略),这和我们讨论的(1+1)维NLS方程的PS、AB、KM 和其他高阶怪波诱导的单(包括双、多)线怪波所具有的短寿命特征完全不同.在(1+1)NLS 模型中AB、KM 是一类时间或空间周期性演化的孤子,它们的极限形态就是PS.但在(2+1)维NLS 方程中可以作为诱导线怪波激发的原型,这为讨论高维非线性模型的怪波问题提供了一个有启迪的途径.

值得指出,我们给出(2+1)维NLS 方程的自相似变换(2)式,其系数α,β,γ在满足(22)式或(26)式下可以自由选取,因此可以讨论包括聚焦(抛物)或散焦(双曲)型的(2+1)维NLS 方程的怪波激发.鉴于在(1+1)维情形,只有聚焦的(1+1)维 NLS 方程才存在怪波激发,深入研究散焦的高维模型显然有很好的理论价值和实际应用,相关的研究进行中.

总之,本文以(2+1)维NLS 方程为模型,发展自相似变换理论,构建了它的二维自相似变换,深入研究了它的多类线怪波激发,并通过图示展现了本文例举的各类线怪波的演化规律.本文揭示的高维怪波激发新机制,丰富了我们对怪波的了解,有助于提升对高维非线性波动模型相干结构的新认识.