结构面特征及应力边界对岩体渗透系数的影响研究
任志善,郭雨非,刘和艺,刘立健,刘 恒
(1.北京市市政工程设计研究总院有限公司,北京 100082;2.中国水利水电科学研究院,北京 100048)
1 研究背景
岩体孕育的大量断层、裂隙、节理等结构面使得岩体的力学特性和水力学特性异常复杂[1-2]。自1970年代以来,国内外大量学者针对裂隙岩体的渗流特性问题展开研究[3-6]。KENJIAOKI等[7]利用节理岩石的若干钻孔估算了岩体三维的渗透系数与单位储水量。张金才等[8]将裂隙岩体假设为互相平行的裂隙网络,研究了岩体的渗透系数随埋深和水力梯度的变化规律。刘才华等[9]针对低围压下节理岩体的渗流提出了半经验理论公式,并通过室内试验与数据分析论证了公式的合理性。随着计算机技术的兴起,数值计算[10-12]方法越来越多地应用于岩体渗流问题研究中。杨天鸿等[13-14]利用自主开发的岩石破裂过程渗流-应力耦合分析系统(F-RFPA),研究了岩体的渗透率在岩石破坏过程中的变化过程。杨金宝等[15]通过随机裂隙网络法计算了节理岩体的渗透张量。张燕等[16]利用两相流理论计算了大开度裂隙网络中渗流速度的分布与变化过程。王玮等[17]针对渗透系数估算模型的影响因子问题,通过整理对比正负相关系数,提出了拟合效果更好的渗透系数估算模型PNC(Positive and Negative Correlation)。李崴等[18]通过研究节理间距、迹长等对反应区域内平均渗透性的表征单元体(REV)及渗透系数的影响,对比了平行流和辐射流情况下二者的异同。
近年来,从岩体结构和形态出发,基于大量野外实测资料,应用概率与统计理论研究岩体中随机结构面[19-21]的方法在工程中得到了广泛应用,然而现有研究中将裂隙产状进行系统考虑,并研究应力边界对节理岩体渗透系数的影响较少,因此本文针对裂隙岩体渗透特性问题,考虑结构面几何形态(倾角、迹长、间距、隙宽)的随机性,利用Monte Carlo[22-23]模拟技术,生成二维结构面分布模型,在此基础上运用渗流等效性[24-25]的相关理论,研究了结构面的几何特征和应力边界对渗透张量的影响规律,为实际工程的应用提供理论和数据支撑。
2 研究方法与模型构建
2.1 计算模型 目前,一般基于流量等效,对裂隙岩体渗透性进行等效化处理,进而分析地下洞室工程、大坝工程、边坡工程等渗流量和渗流压力情况,即利用能够反映研究区域平均渗透性的表征单元体(REV)来表征岩体的连续性。本文利用借用这一方法,通过离散单元软件UDEC(Universal Distinct Element Code)计算不同结构面岩体处于不同地应力环境下的渗透张量变化情况,其计算流程如图1所示,采用的表征单元体见图2,其中图2(a)、图2(b)、图2(c)分别为单组裂隙、双组裂隙和随机裂隙的表征单元体,图2(d)、图2(e)、图2(f)分别为上述表征单元的网格划分。

图1 UDEC的计算流程

图2 计算中采用的表征单元体(REV)
2.2 水力边界条件 为研究几何特征和应力边界的影响,计算中采用相同的水力边界如图3所示:

图3 水力边界条件
以x方向的流量测试为例,左侧为恒定水头边界ΔP;上下两侧是对称的由ΔP减为0的梯度水头边界;右侧为0水头边界。x方向的流量为qyx,单位为m2/s,通过下式计算:

式中:k为渗透系数;i为水力梯度。
对于两组垂直的水力梯度Px,Py,达西定律又可表示为矩阵形式:
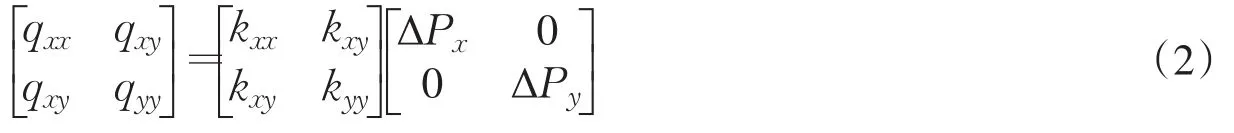

其中:

式中:qxL和qxR分别为x方向流量测试时左侧和右侧的单宽流量;qxT和qxB分别是x方向流量测试时上侧和下侧单宽流量。其余变量同理。计算中各模型取相同的水力边界条件:ΔPx=ΔPy=1 kPa·m-1,当改变模型的节理参数或应力边界条件时,通过UDEC的计算获得各方向的流量,将流量结果与水力边界带入式(3)得到相应的渗透系数。
3 结构面的几何特征对渗透系数的影响
3.1 倾角 针对结构面倾角对渗透系数的影响问题,分别设置了单组裂隙、2组相互垂直的双组裂隙和3组相互间夹角为45°的三组裂隙,研究二维渗透张量随倾角的变化规律,模型参数如表1所示。
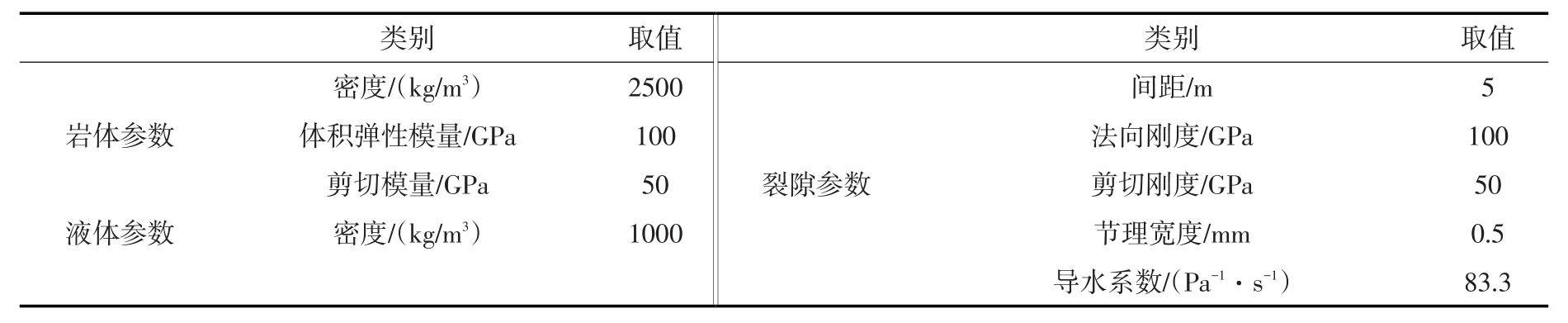
表1 模型参数取值
渗透系数变化情况如图4所示。
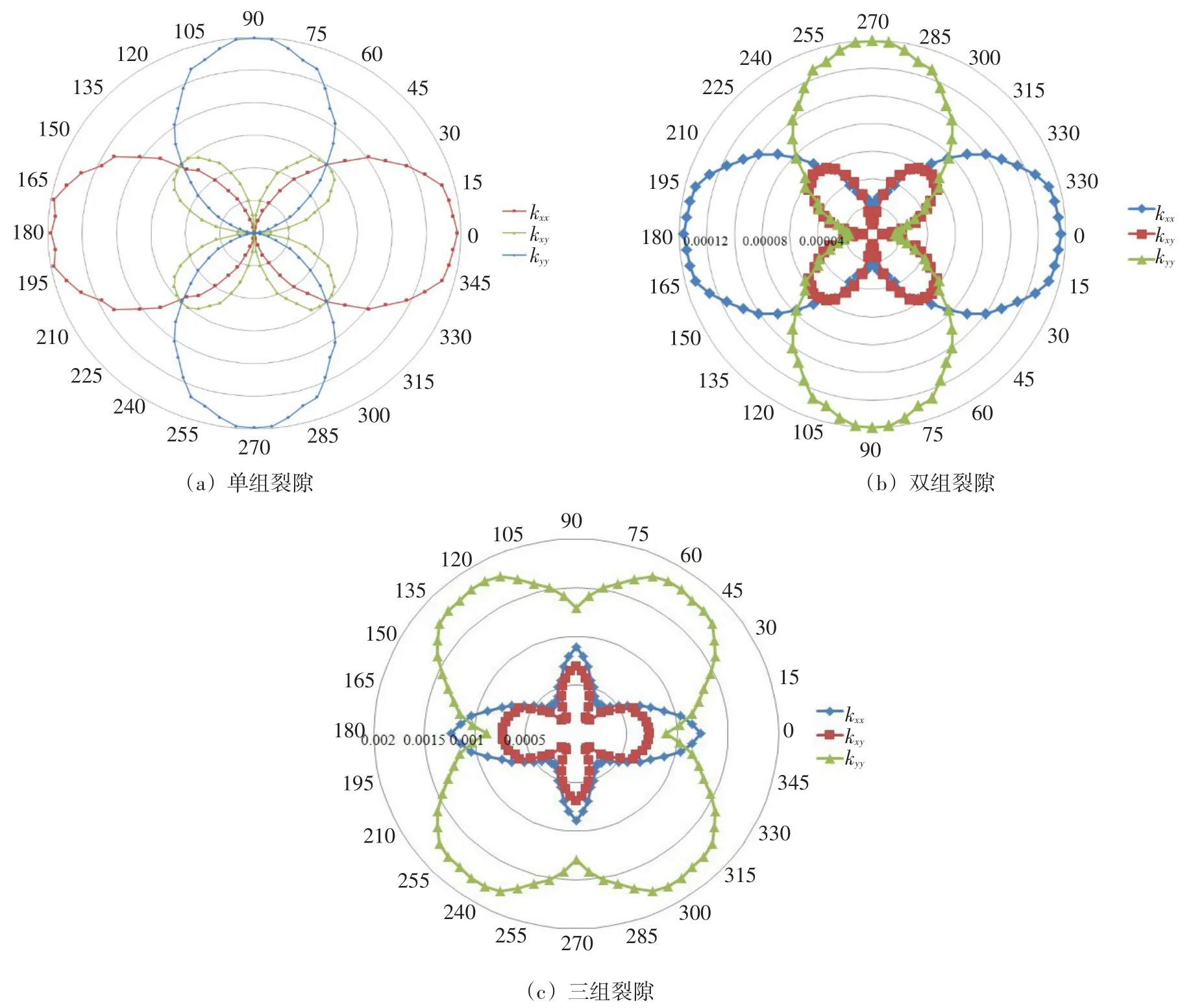
图4 渗透张量随倾角的变化
由图4可知,裂隙倾角对于岩体的渗透性有较大影响。单组裂隙与双组裂隙的变化趋势相似:x方向的渗透系数kxx在倾角为0°和180°时分别达到最大值9×10-5和1.2×10-4,在倾角为90°和270°时分别达到最小值0和4×10-5;y方向的渗透系数kyy在倾角为90°和270°时分别达到最大值9×10-5和1.2×10-4,在倾角为0°和180°时分别达到最小值0和4×10-5;kxy在倾角为45°、135°、225°和315°时分别达到最大值3×10-5(单边裂隙)和6×10-5(双边裂隙),在倾角为0°、90°、180°和270°时达到最小值0。对于三组裂隙,kxx在倾角为0°和180°时达到最大值1.3×10-3,在倾角为90°和270°时为次大值9×10-4,在倾角为60°、120°、240°、300°时为最小值3×10-4。kyy在倾角为60°、120°、240°、300°时达到最大值1.8×10-3,在倾角为0°和180°时达到最小值8.5×10-4;kxy在倾角为0°、90°、180°和270°时达到最大值7.5×10-4,在倾角为60°、120°、240°、300°时达到最小值1×10-4。
可见,岩体的渗透性与裂隙倾角和渗流的主方向相关,节理组的倾角与渗流主方向较为接近时,该方向的岩体渗透系数较高,而与节理成一定角度相交的其他方向的岩体渗透系数较低,同时裂隙组数的增多,会影响岩体各方向的渗透系数,即增加组数会增大渗透张量极值分布的均匀性。
3.2 间距 以倾角60°为例,分别计算单组裂隙与双组裂隙模型在裂隙间距为3 m、5 m、7 m和9 m时的渗透系数,计算结果见图5。
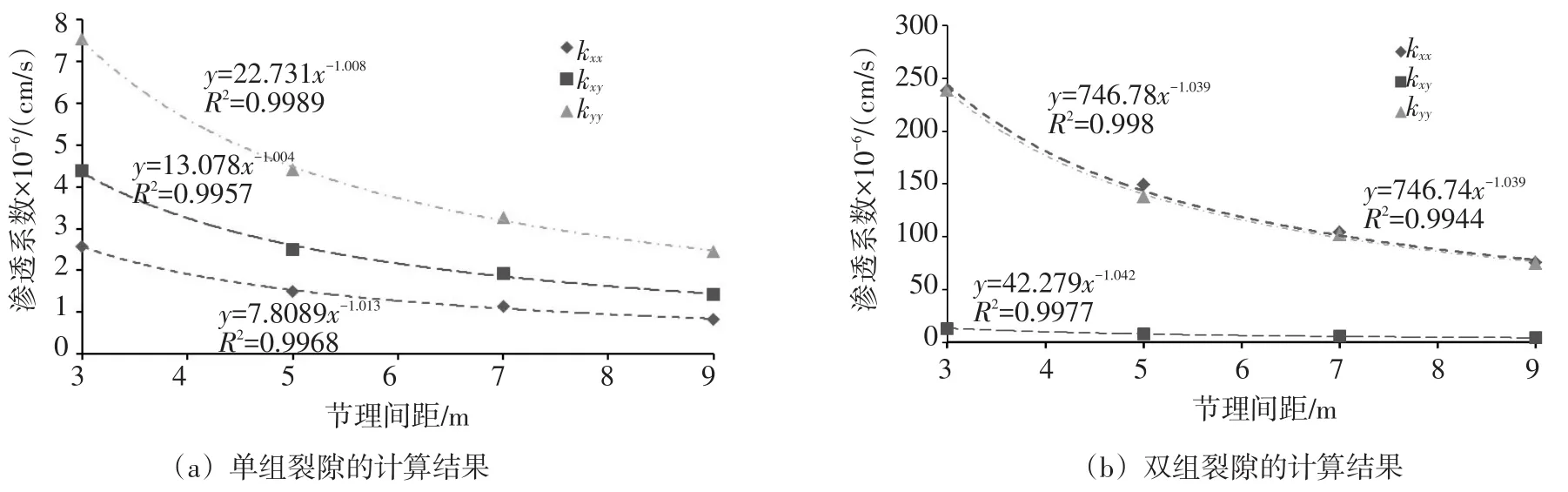
图5 渗透张量随间距的变化
由图5可知,当裂隙倾角为60°时,随着裂隙间距增加,岩体的渗透系数呈幂函数降低趋势。单组裂隙模型中,kxx、kyy、kxy的系数分别为7.8089、22.731和13.078,但三者的指数相差极小,表明在一定距离范围内,kyy对裂隙间距变化的敏感性最强;kxx受裂隙间距变化的影响最弱。双组裂隙模型中,kxx与kyy的系数分别为746.78和764.74,二者受间距变化的影响较大,且变化规律基本一致;kxy的系数为42.279,其对间距变化的响应不明显。在一定的间距变化范围内,双组裂隙的渗透系数量值大于单组裂隙,且变化幅度更大,表明裂隙组数的增多会提高渗透系数随间距变化的敏感性。
3.3 隙宽 研究表明,岩体内部结构面的张开度(隙宽)对岩体的透水性也有较大影响,这里分别计算单组裂隙与双组裂隙模型在不同隙宽时岩体的渗透系数,计算结果见图6。
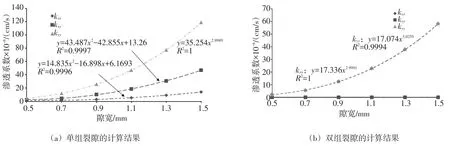
图6 渗透张量随隙宽的变化
可以看出,岩体各渗透分量均随着隙宽的增加而增大,但表现出的变化形式有一定的不同。对于单组裂隙模型,kyy与隙宽基本呈现系数为35.254的幂函数关系(接近立方定理关系),表明其对隙宽变化的敏感性较强;而kxx与kxy的变化规律呈多项式函数关系,受隙宽变化的影响相对较弱。双组裂隙模型中,各分量与隙宽均呈幂函数关系,其中kxx与kyy的系数分别为17.336和17.074,二者受隙宽变化的影响较强,且变化规律基本一致;kxy的幂指数与系数分别为1.9231和0.0206,表明隙宽的变化对其影响不大。隙宽在一定的变化范围内,单组裂隙的渗透系数量值与变幅略大于双组裂隙,表明裂隙组数的减少会增大渗透系数对隙宽变化的敏感性。
3.4 符合统计规律的结构面几何特征影响 实际研究结果表明,自然界中岩体节理的分布符合一定的统计规律,这里采用假设结构面特征服从一定的统计概率模型,根据统计数据(表2),设置随机裂隙的表征单元体的间距服从均值为0.3 m的负指数分布,同时设置倾角和迹长分别服从正态分布(均值为60°)和对数正态分布(均值为8 m),通过分别改变其均值,研究倾角和迹长对于渗透特性的影响。
3.4.1 倾角 结构面的间距和迹长满足表2所示的概率模型,倾角则服从正态分布,均值由0°开始增大至90°,标准差为10°,计算结果如图7和图8所示。

表2 计算倾角影响时的统计概率模型(改变倾角均值)

图7 渗透张量随倾角的变化(服从统计规律)
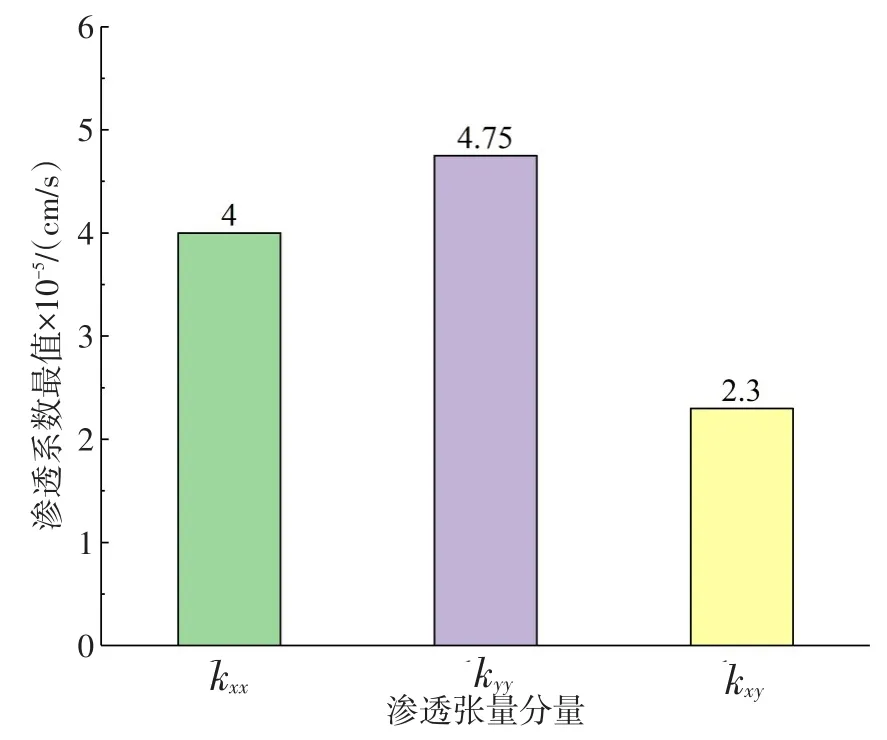
图8 各渗透张量分量的最值
由图7和图8可知,kxx与kyy随倾角与其渗流主方向的接近而增大,kxx在倾角为0°和180°时达到最大值,在倾角为90°和270°时达到最小值;kyy在倾角为0°和180°时达到最小值,在倾角为82°~98°和262°~278°时达到最大值,kxy在倾角为 45°、135°、225°和315°时达到最大值,在倾角为0°、90°、180°和270°时达到最小值。对比各渗透分量的最值,kxy的最大值是kxx的57.5%,是kyy的48.4%,因此在满足一定的统计规律条件下,kyy受倾角的影响最大,kxy受倾角的影响较小。
3.4.2 迹长 在非完全贯通的裂隙情况下,裂隙作为导水通道,其迹长势必影响岩体的透水性。在倾角和间距满足表2所示的概率模型条件下,以1 m为间隔计算渗透张量随迹长的变化过程,计算结果如图9所示。

图9 渗透张量随迹长的变化(服从统计规律)
可以看出,裂隙迹长为1~2 m时,水平及竖直方向的渗透分量均为0,即未有渗流通道存在。各渗透张量分量均随裂隙迹长的增加而增大,其中kxx对迹长变化的敏感性较强;各分量的增长速度由快变慢,当迹长增加至7 m后,渗透系数变幅较小,原因是裂隙迹长增加至一定长度后相互贯通,在计算范围内已形成透水通道。
4 应力边界对渗透系数的影响
4.1 特定节理 自然界中岩体在地应力的作用下,深部裂隙可能部分闭合,同样开挖卸荷情况下,洞壁岩体历经应力路径不同,对裂隙的闭合度也产生相应的影响,进而影响岩体渗透特性。这里通过应力-渗流耦合模型,分别计算单组裂隙和双组裂隙模型在水平和垂直方向上的应力边界由0增大至10 MPa时渗透张量的变化过程,其中特定节理下的计算模型采用图2(a)、图2(b)所示的贯穿单、双组裂隙单元体,材料参数的取值为表1,倾角则以60°为例,统计规律的节理计算采用图2(c)的随机裂隙单元体,参数取值见表2,计算结果如图10所示。
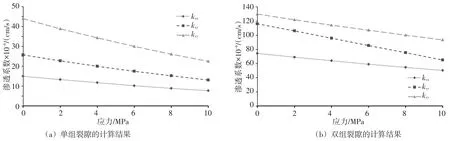
图10 渗透张量随应力边界的变化
由图10可知,随着应力水平的提高,节理岩体的渗透系数逐渐降低,近似呈线性函数关系,原因是高应力导致有效水力隙宽减小,进而降低了岩体的透水性。单组裂隙模型中,kyy的斜率以及y轴上的截距均大于其余的渗透分量,表明该方向上的透水性更强,对应力变化的响应更剧烈。双组裂隙模型中,kxx与kyy的斜率接近,但kyy在y轴上的截距更大,同时kxy的斜率明显更高,表明其受应力变化的影响更大。对比不同裂隙组数的计算结果,双组裂隙模型渗透系数的量值与变幅均大于单组裂隙模型,表明裂隙组数的增多提高了边界应力对岩体渗透特性的影响。
4.2 符合统计规律节理 根据3.4节确定的结构面几何特征概率模型(表2),计算应力边界对岩体渗流特性的影响,如图11所示。
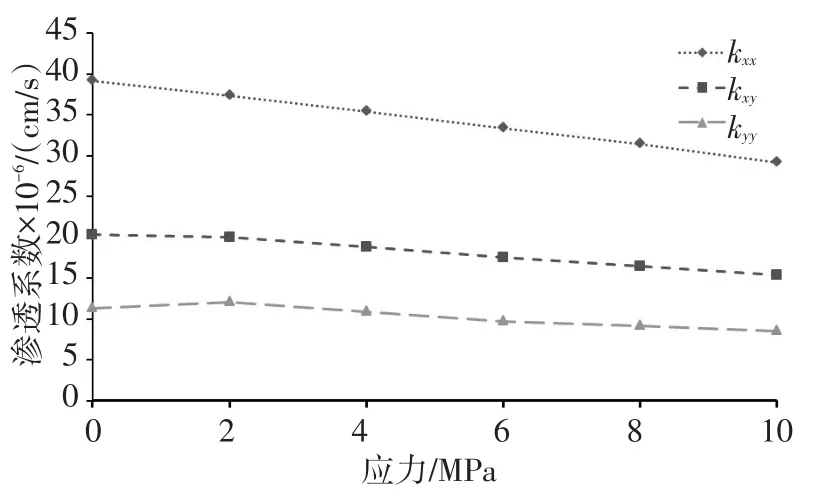
图11 渗透张量随应力边界的变化(服从统计规律)
由图11可知,虽然随机节理的生成具有一定的不确定性,但渗透分量随应力边界的变化基本保持线性关系,渗透系数随应力水平的提高而减小。其中kxx的降幅速度较快,且该分量在y轴上的截距更大,表明其对应力变化的敏感性较强,该方向上的透水性也较强。kxy分量则整体基本保持不变,受应力变化影响较小。
5 结论
本文利用UDEC软件,通过多个数值分析模型,分析了结构面的几何特征和应力边界条件的改变对裂隙岩体等效渗透性的影响,结果表明:
(1)裂隙倾角、间距、迹长及隙宽等对于岩体渗透特性均有较为明显的影响。倾角与渗流主方向较为一致时,一般与裂隙平行方向的方向渗透系数较高。裂隙间距越大,岩体渗透系数越低,各渗透张量分量与间距基本呈幂函数关系。岩体各渗透分量均随着隙宽的增加而增大,但表现出的变化形式有一定的不同。节理迹长为1~2 m时,水平及竖直方向的渗透分量均为0;迹长为2~7 m时,岩体渗透系数随迹长的增加而增大,但增加趋势由快变慢;迹长增加至7 m后,由于透水通道的形成,各渗透系数变幅较小。
(2)岩体所赋存环境的地应力场环境对于岩体的渗透系数具有明显影响,当地应力量值增加时,一般会降低岩体渗透特性,且岩体渗透系数与地应力量值基本呈线性关系。

