椭圆曲线y2=x3+(m-4)x-2m的整数点
高志鹏,牟全武
(西安工程大学 理学院, 陕西 西安 710048)
1 引言及主要结论
1987年, ZAGIER构造了一批具有大整数点的椭圆曲线[1]。例如, 他指出椭圆曲线
y2=x3+27x-62
(1)
有大整数点
(x,y)=(28 844 402,±154 914 585 540)
运用代数数论与p-adic分析方法, 文献[2]证明了椭圆曲线(1)仅有整数点
(x,y)=(2,0),(28 844 402,±154 914 585 540)
文献[3-4]对文献[2]的结果给出了简化证明。一般地, 设m为任意整数, 求椭圆曲线
y2=x3+(m-4)x-2m
(2)
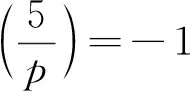
定理1设p,q为奇素数,且满足p≡17(mod 24),m=6p-8=3q+1, 则椭圆曲线(2)除整数点(x,y)=(2,0)外,至多只有2个整数点:
(x,y)=(24pu2v2+2,±12puv(u4+12qv4))
这里u,v∈N+且满足(u2-6v2)2-24pv4=1。
推论1椭圆曲线y2=x3+234x-476,y2=x3+666x-1340,y2=x3+810x-1628,除了整数点(x,y)=(2,0)外, 至多只有2个整数点。
2 引 理
引理1[22]若D是一个非平方的正整数,则不定方程
x2-Dy2=1
(3)
得出,其中n是任意正整数。
引理2若D是一个非平方的正整数, 则不定方程x2-Dy4=1至多有2组正整数解(x,y), 而且该方程恰有2组正整数解的充要条件是
D∈{1 785,28 560}
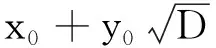
证明见文献[23]中的引理2。
推论2若D为正偶数且D≠28 560, 则不定方程
x2-Dy4=1
至多有1组正整数解(x,y)。
证明可由引理1及引理2直接推出, 或见文献[24]中的引理3。
3 定理1的证明
由p、q为素数,且满足p≡17(mod 24),m=6p-8=3q+1,得p≡1(mod 8),q=2p-3,q≡7(mod 8)。设(x,y)是椭圆曲线(2)的整数点,因为
y2=x3+(m-4)x-2m=(x-2)(x2+2x+m),
x2+2x+m>0
所以x≥2。 显然椭圆曲线(2)有平凡整数点(x,y)=(2,0), 下面仅考虑x>2的情况。
设d为x-2与x2+2x+m的最大公因数, 则
d=gcd(x-2,x2+2x+m)=
gcd(x-2,m+8)=gcd(x-2,6p)
且存在正整数a与b使得
(4)
由d|6p知d∈{1,2,3,6,p,2p,3p,6p}。由式(4)消去x得
(5)
以下分8种情况讨论:
情形1若d=1, 由式(5)得b2-(a2+3)2=3q, 解得:a2=3p-8,b=3p-4; 或者a2=p-6,b=p。注意p≡1 (mod 8), 所以a2≡3 (mod 8)。与a2≡1 (mod 8)矛盾。
情形2若d=2, 由式(5)得b2≡2a4+6a2+3p≡2a2(a2-1)+3≡3 (mod 8),不成立。
情形3若d=3, 由式(5)得b2≡3a4+6a2+2p≡3a4-2a2+2≡2,3 (mod 8),不成立。
情形4若d=6, 因为p≡2 (mod 3), 所以由式(5)得b2≡6a4+6a2+p≡p≡2 (mod 3), 不成立。
情形5若d=p, 由式(5)得b2≡pa4+6a2+6≡a4-2a2+6≡5,6 (mod 8),不成立。
情形6若d=2p, 由式(5)得b2≡2pa4+6a2+3≡2a4-2a2+3≡3 (mod 8),不成立。
情形7若d=3p, 由式(5)得b2≡3pa4+6a2+2≡2 (mod 3), 不成立。
情形8若d=6p, 由式(5)得b2=6pa4+6a2+1, 即b为奇数。如果a为奇数, 那么从p≡1 (mod 8)及a2≡1 (mod 8)可推出b2≡5 (mod 8), 不成立。故a为偶数, 进而得知b+3a2+1与b-3a2-1都是偶数。注意2p-3=q, 由b2=6pa4+6a2+1得
(6)
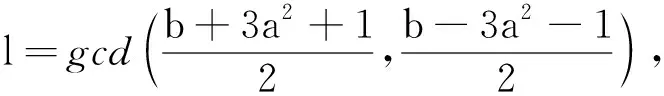
情形8.1b+3a2+1=6qr2,b-3a2-1=2s2,a2=2rs。
由前2个式子得3a2+1=3qr2-s2, 等式两边模3得s2≡2 (mod 3), 不成立。
情形8.2b+3a2+1=6r2,b-3a2-1=2qs2,a2=2rs。
由前2个式子得3a2+1=3r2-qs2,显然3不整除s。等式两边模3并利用q≡1 (mod 3)及费马小定理得1≡-1(mod 3), 不成立。
情形8.3b+3a2+1=2qr2,b-3a2-1=6s2,a2=2rs。
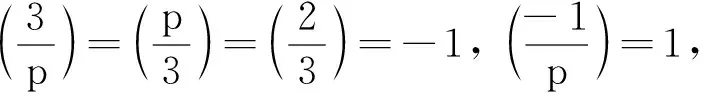
情形8.4b+3a2+1=2r2,b-3a2-1=6qs2,a2=2rs。
由上面3个式子及q=2p-3得
6ps2+1=(r-3s)2
(7)
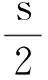
(u2-6v2)2-24pv4=1
(8)
根据推论2, 不定方程X2-24pY4=1最多只有一组解(X,Y)。当方程(8)有解时, 有
x=da2+2=24pu2v2+2
y=±dab=±12puv(u4+12qv4)
即此时椭圆曲线(2)至多有2个整数点(x,y)=(24pu2v2+2,±12puv(u4+12qv4))。
综上, 定理1得证。

