智能循迹货车与乘用车小角度侧碰速度推算模型研究

都雪静，梁文智，沈亚敏

(东北林业大学 交通学院， 哈尔滨 150040)

截至2019年底，我国拥有的公路营运载货汽车已达1 087.82万辆，约占民用机动车保有量的3.87%，而2019年因汽车类交通事故导致的死亡为56 924人，约占道路交通事故死亡人数的90.69%。在中国“严重交通事故”(SRTCs)与“特别严重交通事故”(PSRTCs)成因统计中，超速和超载是事故发生的主要原因，分别占交通事故的66.3%和32.6%[1]。由此可见，超速是交通事故发生的关键问题之一。在事故成因调查方面，事故现场车辆位置、底盘变形、设施损坏、天气状况等细节信息收集能力通常较为有限[2]，因此，分析事故发生时的车速，成为道路交通事故成因和事故认定的重要依据[3]。

在碰撞事故车速推演方面，Iwata K等[4]采用三维扫描事故现场，还原事故发生前的车辆运动状态；Vangi D[5]与Mchenry B G等[6]采用研究车辆碰撞后变形量的方法求解汽车碰撞车速；刘永涛等[7]采用道路交通事故分析与再现系统(crash view)推算实际场景的车速，但在实际货运车辆事故运用方面时效性不佳。车辆碰撞事故发生后，散落物大量存在，其特征参数可以为碰撞发生时速度的推算提供线索，有学者对车辆发生碰撞后的散落物运动特征进行研究，运用抛射距离对碰撞速度进行推演，并建立了汽车碰撞散落物广义运动理论模型[8]，但最远抛距这一参数在实际应用中条件有限，相较于货车碰撞后的散落物分布形状、面积及质量等特征，获取难度较大。

5G网络相较于4G可以为智能货车提供更加稳定的信号连接[9]，利用5G网络的特点，可以对智能货车进行部署定位、路径规划、任务调度、运动控制、信息融合等应用[10]，因此，近年来，为了提高生产效率，智能载货汽车开始普及。2018年里约热内卢的Tinto集团在1 700 km的道路上运营了世界上第一批智能驾驶货车[11]；日本机械制造商Komatsu在加拉曼岛进行了100 t大型无人矿用自卸车的试运行[12]；Salem等[13]利用1∶24的装载机及自卸货车进行了基于web平台的云计算能力进行了装载、托运及卸货试验；刘西等[14]以真实车辆1∶10的缩微智能车辆模型，对基于模糊控制算法和PID控制算法实际的缩微智能车巡航控制器进行了验证。在车辆路径规划方面，Zhang等[15]使用基于支配排序的遗传算法(DBCDP NSGA-I1)对无人驾驶矿车的作业路线、调度方案进行多目标优化；高伟健等[16]利用GPS和BDS测量的轨迹，提出了基于CORS定位的无人驾驶路径跟踪方法。因此，智能货车是今后的主要应用方向，而智能循迹货车的碰撞事故再现，更是亟待解决的问题。

基于以上问题，以散落物分布形状、面积及质量为对象，选取事故中驾乘人员生命安全威胁极大的小角度侧面碰撞环境[17]，采用1∶20的智能循迹货车与乘用车模型进行碰撞试验，运用坐标法分析4种散落物的分布特性，运用数学建模的方法对货车散落物特征参数进行建模，并对碰撞时发生的速度进行推算。为今后智能循迹载货汽车碰撞事故的再现提供依据。

1 货车与乘用车侧面小角度碰撞试验

1.1 实验设备

图像采集设备PH-210NW型号摄像机(图1)性能参数：焦距f=6 mm/8 mm/12 mm，帧速=25 fps，质量为2 500 g，像素为210万像素，可见光有效距1～30 m，最高分辨率为Full HD/1080P(1 920×1 080)+Full D1。

图1 PH-210NW型号摄像机

试验车辆模型采用由环保材料ABS制成的1∶20的满载质量为3.4 kg的载货汽车(图2(a))和质量为0.34 kg的乘用车车模(图2(b))。

图2 车辆模型

其中，货车车模采用STM32F103RCT6为控制芯片，电路原理如图3所示。

图3 控制芯片电路原理图

电机驱动模块(图4(a))采用双H桥L298N逻辑电路，5路光电红外循迹模块(图4(b))采集道路信息，380航模马达(图4(c))后轮驱动TBSN-K20数字舵机(图4(d))。

图4 货车驱动与循迹部分零件

循迹货车的传感器模块采用ATK-MPU6050三轴加速度加三轴陀螺仪的六轴传感器模块(图5)。

乘用车车模的控制精度要求略低，所以采用了两路光电传感器的设计方案，控制芯片使用工作电压范围宽、消耗电流小的LM393双路差动比较器。

1.2 模拟碰撞群体散落物试验方案

考虑到在汽车碰撞事故中，影响群体散落物分布的主要有碰撞类型、碰撞速度和散落物材料3个影响因素，且本文主要研究的是小角度侧面碰撞，因此，将智能循迹货车碰撞时的运行速度、散落材料2个因素作为模拟碰撞试验的影响因素。

图5 ATK-MPU6050六轴传感器模块电路原理示意图

货车载荷高，冲击力大，且在实际碰撞事故中，对基础设施及被撞击车辆造成的损伤更大，因此，将智能循迹货车设定为主动碰撞方，将乘用车设定为被动碰撞方。

针对现有L3级别自动驾驶循迹车辆普遍速度不高的情况，且对山东派蒙公司生产的智能循迹车辆研究后，将本实验中货车模型的速度上限定为10 km/h，乘用车模型的速度恒定设为1.2 km/h，在保证车辆有足够碰撞能量，能够在碰撞时产生足够大的碰撞力的条件下，设定最低速度6 km/h。在此速度区间以0.5 km/h的间隔取9组速度，进行不同速度下的碰撞试验。

货车所装载散体的选取：为了研究常见的车载群体散落物对分布特征的影响，选用颗粒间只具有内摩擦力而无黏聚力的无黏性散粒体作为散落物材料，选择大豆、玉米、大米和瓜子4种材料进行散落试验，研究不同材料对分布特征的影响。试验方案如表1。

表1 模拟碰撞试验方案

1.3 模拟碰撞群体散落物试验条件

选择干燥、水平的实验室地面作为试验场地，实验室内比较宽阔无阻挡群体散落物的障碍物，整个试验在无风的条件下进行，搭建试验跑道如图6所示。

图6 试验跑道示意图

1.4 模拟碰撞群体散落物试验流程

碰撞场地跑道铺设，应注意跑道不宜过宽且保证长度、平滑度与完整性，碰撞处缓冲区面积尽量大，保证散落物能自由散落及车辆碰撞完后停车。碰撞试验流程如图7所示。碰撞过程用高速摄像机拍摄散落物的散落范围，如图8所示。

碰撞后用每小格5 cm×5 cm的坐标纸覆盖，如图9所示，排除有较大离群趋势的单个颗粒强影响点，以碰撞点为原点建立坐标系，勾勒出群体散落物分布的形状，称量散落物质量。

图7 碰撞试验流程框图

图8 实验碰撞实景

图9 散落物记录实景

2 散落物分布特征分析

2.1 散体颗粒力学分析

2.1.1货箱受力分析

散体中力的传递规律不同于液体，散体在无侧向膨胀的条件下受压时，其所受压力以一定比例向其垂直方向传递。

货箱中散体的垂直压力Pz为散体的自身重力作用，因此有：

Pz=zγu

(1)

式中：γu为散体的容量；z为距散体表面深度。

货箱壁所受由Pz产生的侧压力Px为：

(2)

式中：ξ为侧压力系数;φ为散体处于应力最大偏角。

2.1.2货箱内散体切向摩擦力分析

因所选散落物种类可视为刚体，货车货箱内两颗粒件的受力如图10所示，颗粒i与j之间的切向相互作用力为库仑摩擦力，为：

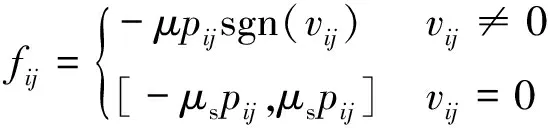
(3)

式中：μ为颗粒i和j之间的滑动摩擦系数，而μs为静摩擦系数。pij为接触点O处i对j的法向压力，而vij为接触点处切平面内物体i相对于物体j的滑动速度，sgn为符号函数。

图10 刚体i与j碰撞受力示意图

由牛顿第三定律可知，当位于货箱z深处时，pij与Pz分散到单个颗粒上的Ps数值相等。

(4)

式中：n为货箱横截面颗粒的个数。

因此，将式(4)代入式(3)可得fij(z)表达式：

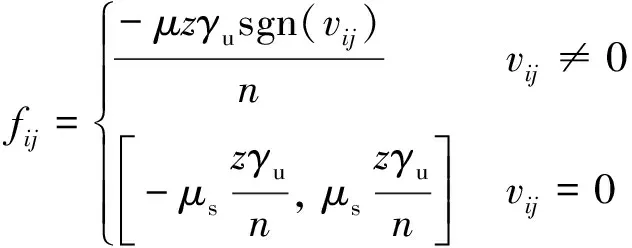
(5)

式中：fij为散体颗粒间的切向摩擦力。

由式(4)可以看出，随着货箱深度的减少，颗粒间的切向摩擦力数值减少，货箱内货物表层颗粒更易脱离，与实验中显示出的效果一致。

2.1.3散落物与地面单点碰撞

在颗粒脱离货箱后，本文根据所需要的领域与颗粒几何形状的不同，以大豆颗粒为例，将其视为二维偏心圆盘来分析颗粒与地面单体碰撞，颗粒与地面滑动摩擦系数为μ1，静摩擦系数为μs。

如图11中半径为r的圆盘，其圆心为O1点，其质心为Oc点，初速度为v0和初角速度为ω0。

图11 颗粒与地面之间的二维碰撞示意图

设质心Oc位于O1x1轴，颗粒在重力作用下与地面发生碰撞，则由圆心的平动和绕圆心的转动角度建立坐标系q=[x，y，θ]T，圆盘的运动方程为：

(6)

式中：f与p分别为切向的摩擦力和法向的接触力。

当y≥r时，颗粒与地面无接触，f与p均为0，将运动方程积分可得运动状态。

通过以上分析，还原了颗粒从货箱到与地面碰撞的过程，从中可以看出，颗粒与地面接触后若发生滚动弹跳，其位移较大，从宏观角度考虑，散落物散落面积与形状也会发生较大变化。

2.2 散体分布特征分析

以(0，0)为两车碰撞点，将同一材料不同速度碰撞后的分布形状绘制出来，如图12～15所示。可以看出，4种材料散落区域面积随碰撞速度的增加而增大，且散落区域逐渐远离碰撞点。

图12 不同碰撞速度下瓜子散落物分布

图13 不同碰撞速度下大米散落物分布

图14 不同碰撞速度下玉米散落物分布

图15 不同碰撞速度下大豆散落物分布

瓜子分布呈长条状，延X轴的分布宽度变化较小，这是因为瓜子有4种材料中最小的密度和弹性模量，所以在抛射过程中易受空气阻力影响，而与地面单点碰撞后几乎不发生弹跳，多为滑动摩擦，所以损耗的动能较高，其沿Y轴分布的最远点也是4种材料中最小的。

大米分布形状呈长圆状，大米的弹性模量为257～297 MPa，且密度较大，形状较为规则，在抛射过程中动能损失较小，接触地面后发生弹跳后便处于滑动摩擦状态。

玉米与大豆随碰撞速度增大分布变化较大，扩散较为明显，玉米弹性模量为27 MPa，但是其密度较高，抛射距离远；而大豆弹性模量最高，其与地面接触后，产生多次弹跳运动，随后便是较长时间的滚动运动，造成了大豆的散落面积更大。

3 散落物特征参数与速度模型

3.1 回归分析的基本理论

散落物分布特征研究中，多应用回归分析建立不同参数与碰撞车速的数学关系。

回归模型的一般形式为：

y=f(x1,x2,…,xn)+ε

(7)

式中：x1，x2，…，xp为随机变量(自变量)，ε为随机误差，y为因变量。

最小二乘法(又称最小平方法)是一种数学优化技术，使建立的回归方程更好地描述变量间的关系。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使这些求得的数据与实际数据之间误差的平方和为最小。

当需要拟合直线方程形式为：

Y=Ax+B

(8)

则设方程为：

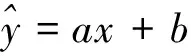
(9)

离差的平方和求解，有方程为：

(10)

展开整理得：

(11)

(12)

因此，离差的平方和为：

(13)

推导后可得:

(14)

观察可得后2项为常数，因此，令：

(15)

即可得到最小值Q，因此：

(16)

当需要进行多项式拟合时，有：对于给定的1组数据(xi，yi)(i=0，1，…，m)，求作n次多项式n≤m，其形式有：

(17)

使其满足条件Q的值最小，Q表示为：

(18)

整理可得：

(19)

SPSS在曲线回归分析中，可以拟合11种常见曲线的回归方程。本文通过观察各个参数的散点图，选取合适的曲线模型进行拟合。

在一元非线性回归中，通常根据剩余残差平方和Se(残差平方和)、剩余标准差σ或复相关系数R2这3个量中的任何一个来决定回归方程的优劣，Se、σ小者为优，R2大者为优。

根据回归统计分析相关知识，可以得知：

(20)

(21)

(22)

其中lyy为：

(23)

本文只要以R2为参考，选取拟合曲线，为了方便计算尽可能选取次数低的多项式。

3.2 散落物面积与速度的数学模型

通过测量与计算可得到散落物面积与速度的数值，如表2所示。

表2 散落物面积与碰撞速度的数值

以碰撞速度(V)为解释变量，以散落物的散落面积(S)为被解释变量对4种散落物材料(大豆如图16、玉米如图17、大米如图18以及瓜子如图19)分别进行线性模型、对数函数模型、二次曲线模型、三次曲线模型、幂函数模型及指数函数模型6种曲线的拟合，选取符合各种材料的散落物的实际情况的最优函数模型。

图16 大豆S1与V的拟合曲线

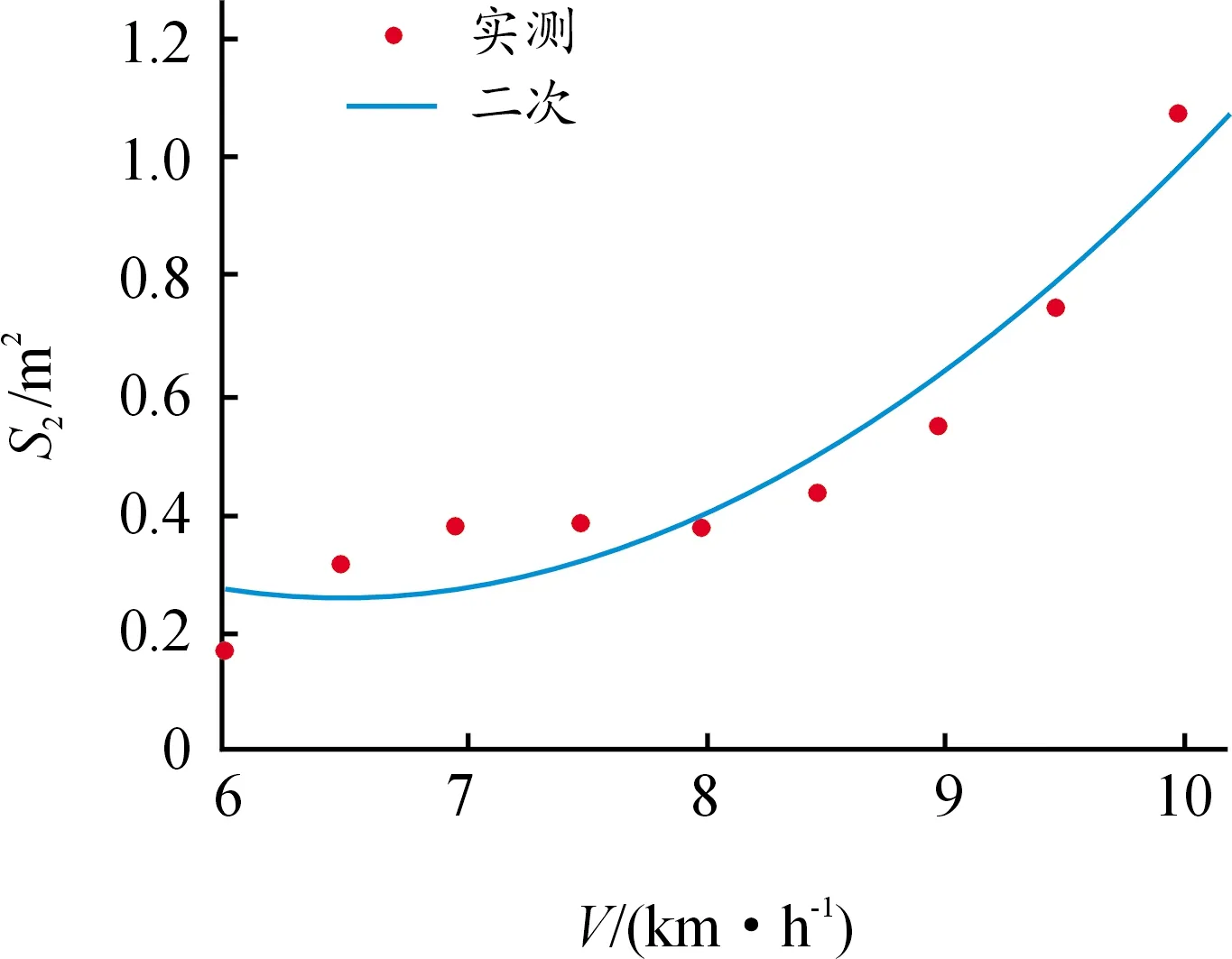
图17 玉米S2与V的拟合曲线

图18 大米S3与V的拟合曲线

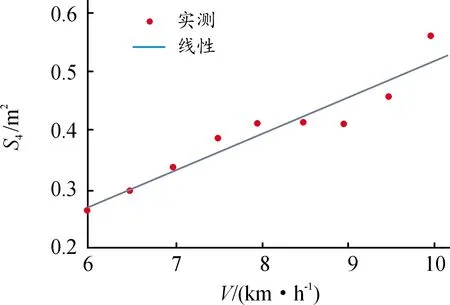
图19 瓜子S4与V的拟合曲线

大豆散落面积与速度建立回归方程为：

S1=6.879-1.839V+0.131V2

(24)

玉米散落面积与速度建立回归方程为：

S2=2.683-0.75V+0.058V2

(25)

大米散落面积与速度建立回归方程为：

S3=0.935-0.192V+0.018V2

(26)

瓜子散落面积与速度建立回归方程为：

S4=-0.095+0.061V

(27)

式中：S1为大豆的散落面积，S2为玉米的散落面积，S3为大米的散落面积，S4为瓜子的散落面积，单位均为m2；V为散落试验的碰撞速度，单位为km/h。

3.3 散落物质量与速度的数学模型

散落物质量与速度的实验数值如表3所示。

表3 散落质量与碰撞速度的数值

以碰撞速度(V)为解释变量，以散落物的散落质量(m)为被解释变量对4种散落物材料(大豆如图20、玉米如图21、大米如图22以及瓜子如图23)进行6种曲线的拟合，选取最优函数模型。

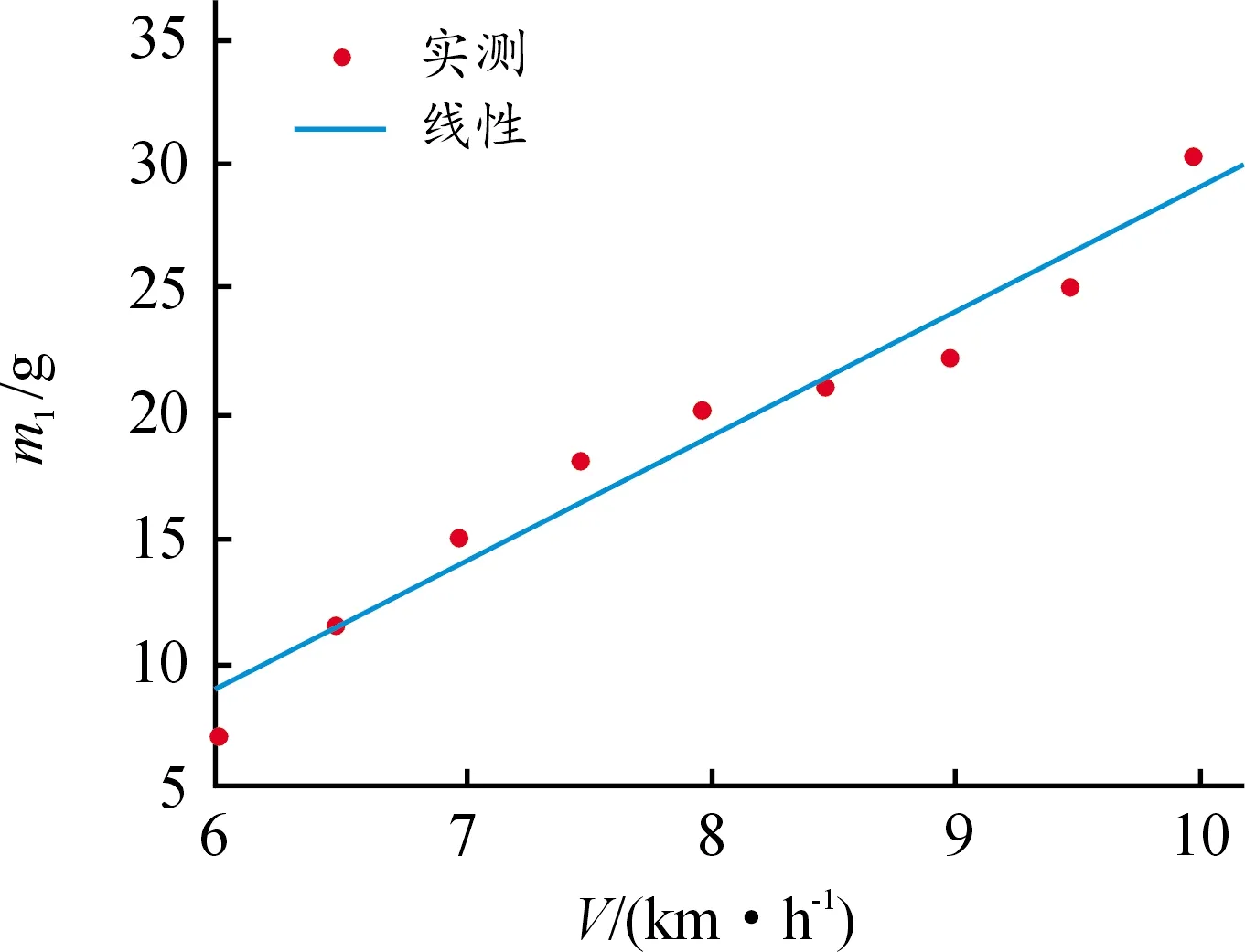
图20 大豆m1与V的拟合曲线

图21 玉米m2与V的拟合曲线

图22 大米m3与V的拟合曲线

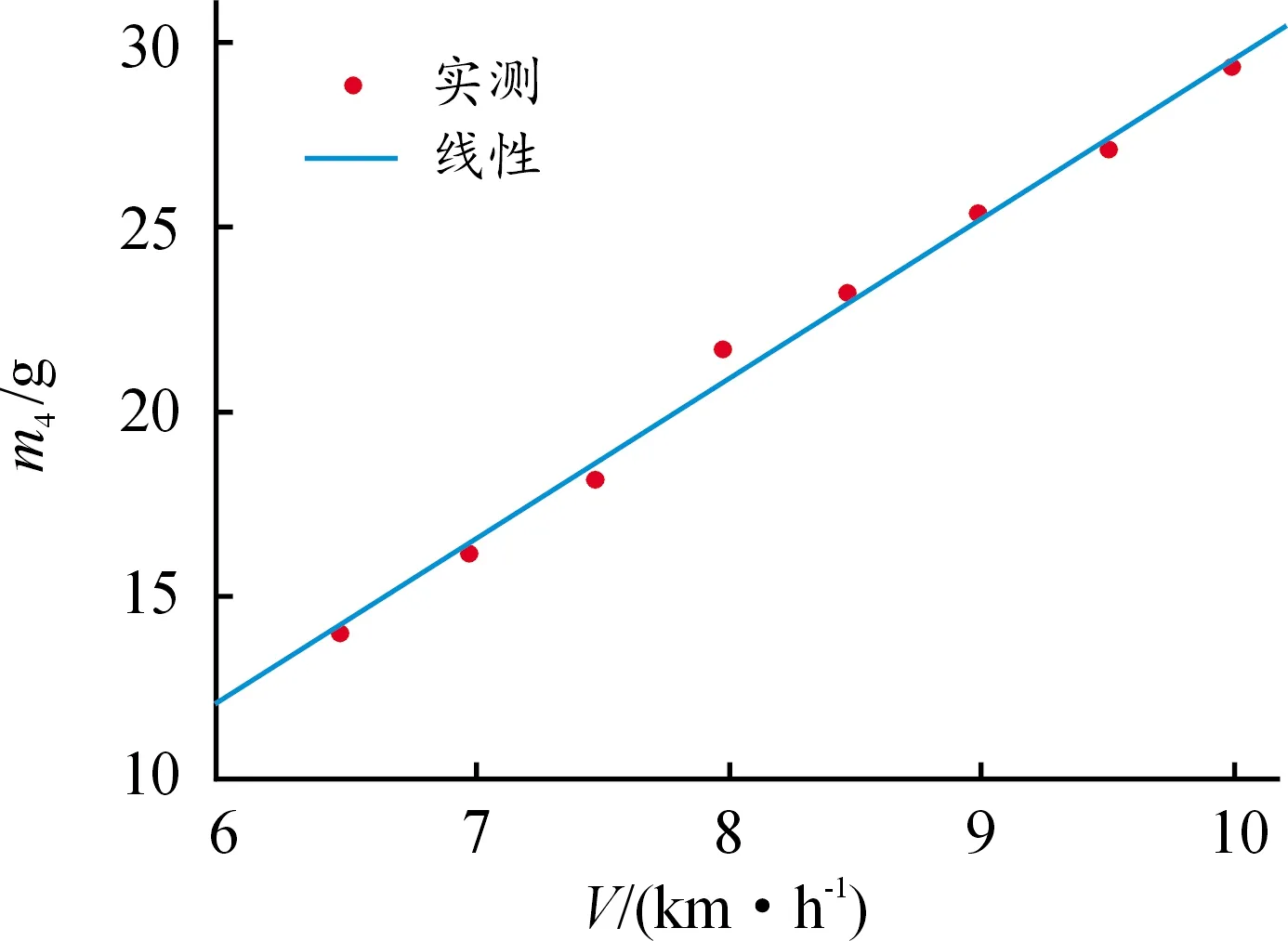
图23 瓜子m4与V的拟合曲线

大豆散落质量与速度建立回归方程为：

m1=-21.218+5.102V

(28)

玉米散落质量与速度建立回归方程为：

m2=-19.136+4.506V

(29)

大米散落质量与速度建立回归方程为：

m3=-20.79+4.706V

(30)

瓜子散落质量与速度建立回归方程为：

m4=-14.11+4.347V

(31)

式中：m1为大豆的散落质量，m2为玉米的散落质量，m3为大米的散落质量，m4为瓜子的散落质量，单位均为g；V为散落试验的碰撞速度，单位为km/h。

3.4 散落物特征参数推算模型

针对4种材料的散落物质量、面积与货车行驶速度三者之间的关系进行探究，采用Matlab R2019a软件中的Curve Fitting Tool拟合工具进行三维的多项式拟合，得到的图像如图24～27。

图24 大豆拟合三维曲面

图25 玉米拟合三维曲面

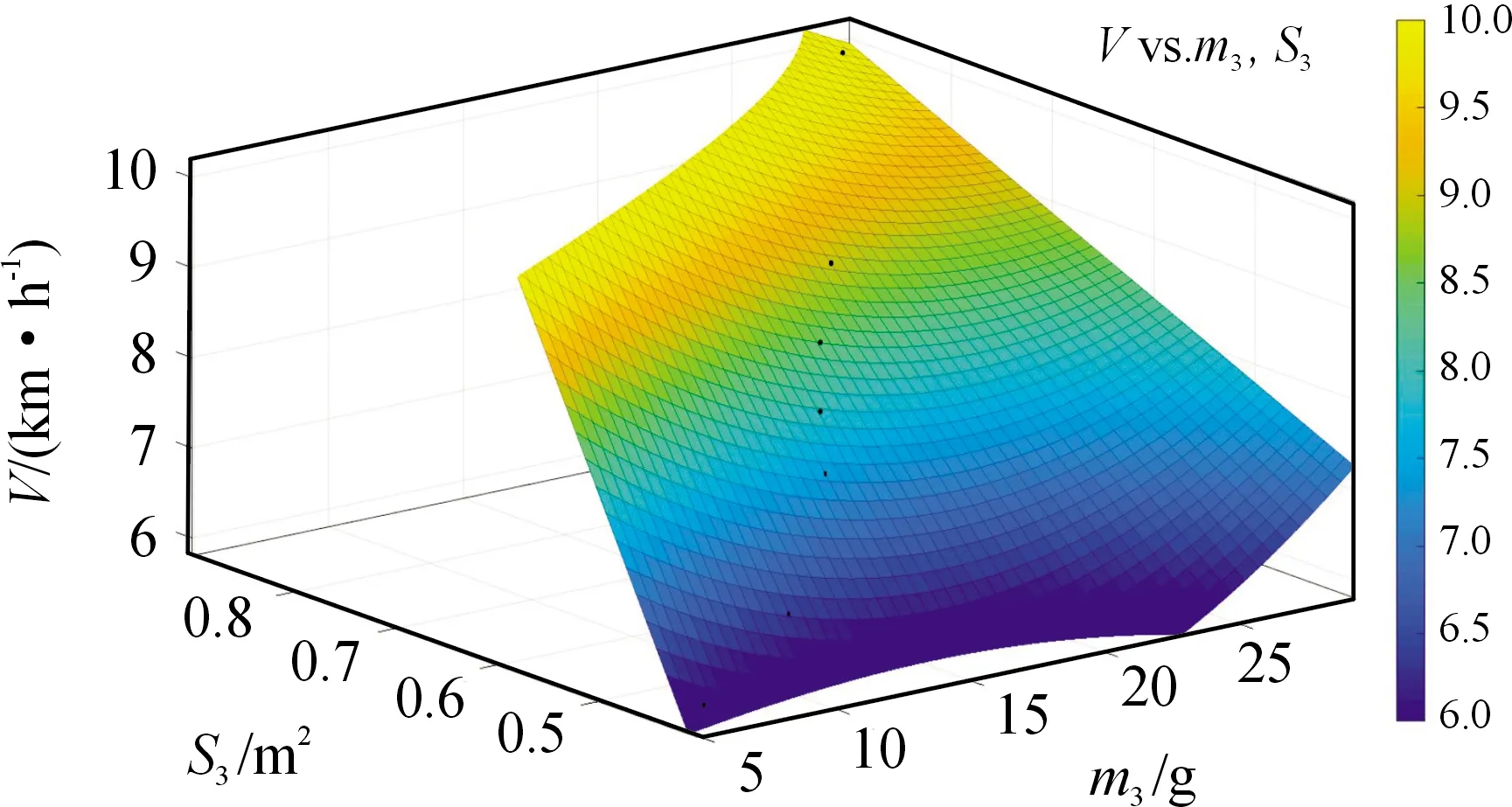
图26 大米拟合三维曲面

图27 瓜子拟合三维曲面

矩阵形式为：

(32)

所拟合数学模型形式(以二次多项式为例)为：

f(x，y)=a20x2+a02y2+a11xy+

a10x+a01y+a00

(33)

在公式选取方面，参照CFTool工具箱结果中给出的参数：误差平方和SSE、确定系数R-square综合考虑确定关系公式。

因计算量和计算难度随多项式次数的升高而变大，在保证拟合精度的前提下，应优先选用低次多项式，因此经筛选后，选用2次多项式。

大豆建立多项式拟合方程为：

0.073m1+7.216S1+3.64

(34)

玉米建立多项式拟合方程为：

V=0.183m2+0.443S2+4.692

(35)

大米建立多项式拟合方程为：

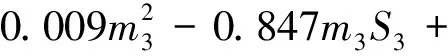
0.107m3+30.28S3-5.654

(36)

瓜子建立多项式拟合方程为：

21.81S4+2.374

(37)

4 结论

采用1∶20的智能循迹货车模型模拟侧面小角度碰撞试验，可有效避免实车碰撞试验成本高及软件仿真不理想的问题，为研究智能货车碰撞提供了新的思路。通过对4种散体的散落形状研究，发现散体颗粒的密度、体积、弹性模量等参数影响散落物的分布形状，因此，对实际智能循迹货车碰撞事故再现时，应当对所装载散体分类。运用最小二乘法理论，建立的智能循迹货车的碰撞速度与散落物的散落面积之间呈二次函数关系，与散落物的质量之间呈线性关系；建立了以碰撞后散落物散落面积及质量为依据的智能循迹货车碰撞速度推算数学模型。相较以往运用散落物最远抛据进行车速推算的模型，数据更易获取，实用性更强，为智能循迹货车发生碰撞事故时的速度鉴定推算提供重要参考。

应关注车辆碰撞后散体的散落过程中颗粒间的相互作用及散体颗粒的弹跳运动等运动学特征；同时智能循迹车辆的主动避障系统的介入对散落特征有很大影响，后续研究中应着重考虑。