基于挥发性成分定量预测风味茶油掺浸出茶油的偏最小二乘回归模型的建立
孙婷婷,陈志清,钟瑾璟,刘剑波,任佳丽,钟海雁,周 波
(林产可食资源安全与加工利用湖南省重点实验室1,长沙 410004)(中南林业科技大学食品科学与工程学院2,长沙 410004)(海普诺凯营养品有限公司3,湖南 长沙 410004)(岳阳市质量计量检验检测中心食品检验所3,岳阳 414000)
油茶(CamelliaOleiferaAbel.)属山茶科(Theaceae)山茶属(Camellia)的常绿小乔木或灌木,与油棕、油橄榄和椰子齐名为世界四大木本食用油料树种[1]。油茶籽油又名山茶油、山茶籽油或茶油,是一种营养和功能丰富的高品质食用油[2-4]。基于茶油营养和经济价值高,以次充好、掺杂使假、以假顶真的市场现象较普遍[5],故建立科学、快速、有效的茶油掺伪检测方法是维护茶油正常市场秩序,保护合法生产经营者和消费者权益的必然要求。
茶油掺伪鉴别主要是采用先进的实验仪器和检测技术,运用数学统计分析方法,从大量复杂的结构化量测数据中挖掘提取出掺伪鉴别所需的特征信息[6]。目前研究充分的量测数据包括脂肪酸、挥发性成分、活性伴随物及其他理化指标。茶油掺伪鉴别研究大多集中在检测手段和分析方法上探讨,如常规理化检测法[7]、色谱法[8-10]、核磁共振法[11]、近红外光谱法[12,13]、拉曼光谱法[14]、荧光光谱法[15]、电子鼻技术[16]及时间分辨荧光技术[17]等,这些技术能很好地实现茶油掺伪其他油脂的定性判断和较好的定量鉴别,但难以实现压榨风味茶油掺浸出茶油的定性和定量鉴别。采用红外光谱技术结合不同统计分析方法,如红外光谱透射模式与透反射模式结合判别分析(DA)[18]和主成分分析(PCA)[19],傅里叶变换红外光谱仪结合偏最小二乘法(PLS)、支持向量机(SVM)和BP人工神经网络(BPANN)[20]等,可实现压榨纯茶油与浸出茶油的定性判别,但难以实现定量鉴别。基于我国风味茶油产品分类分级体系缺乏、感官品质评价技术不完善、茶油风味品质调控不精准和风味茶油相关的结构化量测数据难以确定,导致风味茶油掺浸出茶油的相关研究鲜见报道。本研究提出了茶油的风味和嗜好的定位,定义了茶油原香、浓香(烤香)和果香等8种正面描述语和糊味等10余种负面描述语[21-24],创制了清香型、果香型和浓香(烤香)型3种风味茶油的双适度(籽适度烘焙调风味、榨后适度精炼保风味)制油新工艺[25-30]。
风味茶油和浸出茶油的主要区别在于其挥发性成分的组成及其含量不同,其受油茶栽培品种、环境和加工工艺影响,所以定性和定量判断风味茶油掺浸出茶油的关键在于采用何种检测技术和数据统计分析方法来挖掘和提取出掺伪鉴别所需的信息。本研究基于通过HS-SPME-GC-MS获得的茶油挥发性成分组成及含量,运用Python语言构建了定量预测风味(原香和浓香)茶油掺浸出茶油的偏最小二乘回归(PLSR)模型,以期为风味茶油掺浸出茶油的鉴别研究提供参考,为风味茶油的精准定级分类生产和评价提供技术支持。
1 材料与方法
1.1 实验材料
油茶籽自然晒干后物理冷榨(≤60 ℃),再通过纱布过滤即得原香茶油。原香茶油油样来源于湖南生产的茶油(编号YX1、YX2、YX3)以及本实验室制备(编号YX4)。
油茶籽烘烤干后物理冷榨(≤60 ℃),再通过纱布过滤即得浓香茶油。本研究中的浓香茶油油样分别来源于湖南生产的古茶油(编号KX1)、山柚油(编号KX2)以及实验室制备,具体制备方法:油茶籽120、150、180 ℃下热炒1 h后进行制备的油样分别为KX3、KX4、KX5;150℃下分别热炒10、20、30、40、50 min后制备的油样分别为KX6、KX7、KX8、KX9、KX10。
浸出茶油是油茶饼通过有机溶剂浸提后获得,浸出茶油(编号JC1)来源于于湖南某公司。
1.2 实验方法
1.2.1 实验仪器
7890B/5977A气相色谱-质谱联用仪,毛细色谱柱(HP-5MS,30 m×250 μm×0.25 μm),SPME固相微萃取头(57348-U,50/30 μm DVB/CAR/PDMS),CP224C电子天平,RCT basic加热搅拌器,CA59G榨油机。
1.2.2 茶油挥发性成分的HS-SPME-GC-MS分析
茶油挥发性成分的HS-SPME-GC-MS分析方法及结果参考朱晓阳等[30]的报道,原香茶油及浸出茶油样品共检测出45种挥发性物质成分,浓香茶油样品共检测出56种挥发性物质成分。
1.3 掺伪实验及模型的设计
原/浓香茶油掺浸出茶油设置2个质量分数梯度,自定义为高掺伪梯度(5%、10%、15%、20%、40%、60%、80%)和低掺伪梯度(2%、4%、6%、8%、10%)。高/低掺伪梯度设计的原香和浓香茶油掺伪样本标签设置都为“1”,纯原香和浓香茶油样本标签设置都为“0”。各类样本数据数量及标签设置见表1。

表1 各类样本数据数量及标签设置
1.4 据预处理及编程平台
本研究模型和算法均基于Python 3.7编程语言在PyCharm 2018 IDE平台(JetBrains(Prague), Czech Republic)进行程序编写苹果(Apple Computer Inc.)笔记本,配置为因特尔酷睿i5 CPU(Intel(R)Core(TM)@1.70 GHz),4 GB内存,NVIDIA GeForce 320M显卡。
2 实验结果与分析
2.1 偏最小二乘回归模型掺伪量预测精度分析
利用sklearn.cross_decomposition库中的PLSRegression函数对数据构建PLSR模型,并通过留一法交叉验证,得到不同掺伪梯度下PLSR模型掺伪量预测精度分析结果,见表2。高掺伪梯度下原/浓香茶油掺浸出茶油的掺伪量预测PLSR模型的平均R2值分别为0.998/0.998,平均RMSE值分别为1.127/1.166,决定系数取值较高且均方根误差较低(表2)。低掺伪梯度下原/浓香茶油掺浸出茶油的掺伪量预测PLSR模型的平均R2值分别为0.956/0.999,平均RMSE值分别为0.592/0.094,决定系数取值较高且均方根误差较低(表2)。与高掺伪梯度下的实验结果相比,浓香茶油的平均R2值基本持平,平均RMSE值下降;原香茶油的平均R2值降低,平均RMSE值明显提高(表2)。结果表明PLSR模型定量鉴别原/浓香茶油掺浸出茶油的精准率较高,且对于浓香茶油掺浸出茶油的定量鉴别效果优于原香茶油掺浸出茶油。

表2 不同掺伪梯度下PLSR模型掺伪量预测精度分析
2.2 偏最小二乘回归模型掺伪量预测结果分析
留一法交叉验证下PLSR模型预测原香茶油的掺伪量预测结果分析见表3,PLSR模型预测浓香茶油的掺伪量预测结果分析见表4。PLSR模型对绝大部分样本的掺伪量预测较为准确,预测值与真实值之间的相对误差在0.65以内(表3和表4),但对个

表3 PLSR模型预测原香茶油的掺伪量预测结果分析
别低掺伪质量分数样本的预测效果都较差,如2号真实掺伪质量分数为5%和2%的样本的预测掺伪质量分数与真实掺伪质量分数的相对误差分别达到了0.628和0.612(表3),4号真实掺伪质量分数为5%的样本的预测掺伪质量分数与真实掺伪质量分数的相对误差达到了0.608(表4)。但PLSR模型对浓香茶油低掺伪梯度样本的掺伪量预测比原香更为准确,所有样本的预测的相对误差都比较小,均在0.14以内(表4)。

表4 PLSR模型预测浓香茶油的定量掺伪结果分析
2.3 偏最小二乘回归模型掺伪量预测结果的“真实掺伪量-预测掺伪量”散点图分析
为了能更为直观展示掺伪量预测结果,绘制“真实掺伪量-预测掺伪量”散点图,高掺伪梯度下PLSR模型的掺伪量预测结果散点图如图1所示,低掺伪梯度下PLSR模型的掺伪量预测结果散点图如图2所示。在理想情况下,模型对样本的掺伪量预测完全正确时所有样本点应当全部落在直线y=x上,当样本点越接近直线y=x,模型对样本掺伪量的预测效果越好。
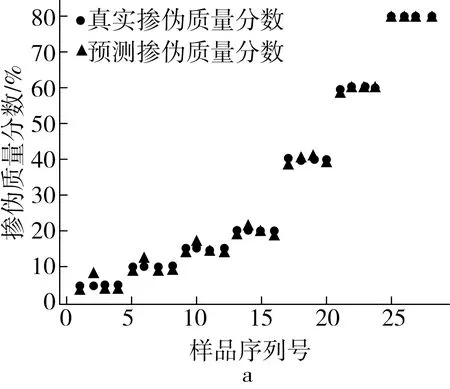
图1 高掺伪梯度下PLSR模型的掺伪量预测结果散点图
如图1所示,高掺伪梯度下,PLSR模型对原香和浓香茶油样本中浸出茶油掺伪量的预测值相对于真实值都存在一定程度的浮动,掺伪质量分数为5%、10%、15%、20%的样本浮动范围较大,掺伪质量分数为40%、60%、80%的样本的浮动范围较小(图1)。在本研究中,PLSR模型对原香和浓香茶油中浸出茶油掺伪量的预测能力随着掺伪质量分数的提高而增强,鉴别精准度提高(图2a和2b),但PLSR模型针对浓香茶油掺浸出茶油的定量鉴别的准确性和稳定性都优于原香茶油掺浸出茶油(图1和图2)。

图2 低掺伪梯度下PLS模型的掺伪量预测结果散点图
2.4 偏最小二乘回归模型掺伪量预测结果的箱型图分析
本研究进一步以箱型图的形式统计了PLSR模型对掺入浸出茶油的压榨原/浓香茶油的掺伪量预测实验中真实值与预测值间的相对误差,不同掺伪梯度下PLS模型的掺伪量预测相对误差箱型图如图3所示。在高/低掺伪梯度下,PLSR模型对原香茶油样本浸出茶油的掺伪量预测较为准确,高掺伪梯度下大部分样本的相对误差集中都在0~0.1之间(图3a),低掺伪梯度下大部分样本的相对误差集中在0~0.15之间,但都仍存在少量离群点的相对误差较高(图3b)。在高/低掺伪梯度下,PLSR模型对浓香茶油中浸出茶油的掺伪量预测较为准确,高掺伪梯度下大部分样本的相对误差集中在0~0.1之间(图3c),低掺伪梯度下大部分样本的相对误差集中在0~0.02之间(图3d),但都仍存在少量离群点的相对误差较高。结果表明,本研究建立的PLSR模型对于浓香茶油掺浸出茶油的定量鉴别的精准率较高,这可能是由于浓香茶油的挥发性成分多,训练集数据多。

图3 不同掺伪梯度下PLS模型的掺伪量预测相对误差箱型图
3 结论
基于高掺伪梯度(5%、10%、15%、20%、40%、60%、80%)及低掺伪梯度(2%、4%、6%、8%、10%)的掺浸出油的压榨油茶籽油的挥发性成分数据,利用偏最小二乘回归算法对原香与浓香压榨油茶籽油掺浸出油茶籽油的掺伪量进行定量预测。
实验结果表明,本研究构建的基于挥发性成分定量预测风味茶油掺浸出茶油的偏最小二乘回归模型的预测能力较强,体现在R2值较高,平均RMSE值较小,相对误差较小。对于原香油茶籽油,PLS模型对高掺伪梯度样本的掺伪量预测的平均R2值达到了0.998,平均RMSE值为1.127,大部分样本的相对误差集中在0~0.1之间;PLS模型对低掺伪梯度样本的掺伪量预测的平均R2值为0.956,平均RMSE值为0.592,大部分样本的相对误差集中在0~0.15之间。对于浓香油茶籽油,PLS模型对高掺伪梯度样本的掺伪量预测的平均R2值达到了0.998,平均RMSE值为1.166,大部分样本的相对误差集中在0~0.25之间;PLS模型对低掺伪梯度样本的掺伪量预测的平均R2值为0.999,平均RMSE值为0.094,大部分样本的相对误差集中在0~0.04之间。

