基坑抢险斜撑撑脚稳定性模型实验及数值分析

黄华，王胜，刘晓明，谭鑫*，周业

(1.中建五局第三建设有限公司，长沙 410116; 2.湖南大学土木工程学院，长沙 410082)

随着中国城市化水平的快速提高，城市地下空间的开发和利用已经成为解决人口、资源、环境问题的重要措施和实施城市可持续发展的重要途径[1]。各类地下空间工程诸如地铁车站、地下停车场、地下商场、人防工程等都需要进行深大基坑的开挖，保证基坑工程的安全成为开发利用城市地下空间的重要前提。尽管目前基坑支护技术和相关理论日趋完善，但由于基坑工程具有强烈的区域性、个体性及高风险性等特点[2-5]，各类基坑事故难以避免。

基坑失稳事故[6-8]可能造成严重的生命财产安全损失，一旦基坑变形达到预警值必须立即对基坑进行抢险加固。朱琦等[9]以实际深基坑项目为依托，阐述了常用的支护结构在基坑施工过程中的力学变形特性。目前常采用的基坑抢险加固措施有两种，一种是在坑底大量回填土方，但通常受限于在市区短时间内获得大量土源。另一种是采用钢管斜撑进行支护[10]，将钢管一端固定于坑底稳定区域，另一端支撑于基坑侧壁，形成斜撑。斜撑能够及时对坑壁形成有力支持，被大量基坑抢险工程所首选采用[11-15]。刘晓玉等[11]通过工程实例介绍了斜撑支护体系在深厚淤泥区域基坑中的应用。刘燕等[12-13]研究了斜撑体系的协同变形承载机理及相应施工方法。但斜撑加固的稳定性往往受到斜撑撑脚地基土体的强度限制，当基坑坑壁稳定需要的抗力过大时易发生撑脚处局部地基失稳。采用浇筑混凝土或钢结构基座能提高斜撑撑脚稳定性[14]，但基座浇铸养护或钢结构焊接施工过程会增加基坑暴露时间，无法满足及时抢险的需求。大量基坑临时抢险采用将无基座斜撑撑脚插入地基，然后装配上部斜撑的方法来迅速处置险情。因此斜撑撑脚地基的稳定性往往成为控制斜撑整体承载能力的关键问题。

目前中外研究主要集中在斜撑结构自身受力状态和对基坑变形的限制效果[14-15]，然而对斜撑撑脚受力变形特征及承载机理问题研究则相对较少，理论体系也并不完善。为此，针对现有研究的不足，选取基坑抢险工程中最为常用的浅埋斜撑撑脚稳定性问题开展了室内物理模型试验和数值分析研究，获得了荷载位移曲线和地基土变形特征，并揭示了斜撑撑脚地基承载机理及破坏模式。

1 物理模型试验

1.1 试验装置

基坑抢险工程应用中使用斜撑进行临时抢险支护时，斜撑与地基土表面的夹角范围大多在30°～60°。因此室内模型实验[图1(a)]的斜撑倾斜角度设置为45°。模型箱净空间尺寸为770 mm(长)×520 mm(宽)×500 mm(高)，模型箱的两侧分别安装透明钢化玻璃，以便观察撑脚地基失稳形式。

h′为加载块竖向位移；s为斜撑轴向位移

根据模型箱尺寸，缩尺模型斜撑钢管选用304不锈钢无缝钢管，直径为50 mm，长度为900 mm，壁厚为2 mm。试验竖向荷载由竖向加载框架上部伺服电机提供，电机最大推拉力能达到50 kN。采用YSF-I/25-4型电动伺服控制系统进行加载控制，可以通过位移、载荷及手摇3种加载方式进行加载的控制，伺服电动缸中安装有压力和位移传感器，可以实现对加载力、速度和位置的精密伺服控制。如图1(b)所示，通过楔形加载块和可以将竖向加载转换为斜撑的轴向荷载。试验的加载采用位移控制，控制竖向传力杆以0.167 mm/s的速度推动楔形加载块匀速下降，直至达到斜撑轴向位移行程(40 mm)或者撑脚地基出现明显破坏。加载过程中传感器每隔1 s采集一次对应时刻的位移和荷载值。模型试验中对埋置长度分别为1倍、2倍、3倍和4倍钢管直径的斜撑进行竖向加载试验。

1.2 模型用土

地基土选用干燥中砂，试验前将所有试验砂放置烘箱内烘干24 h。所选砂土粒径级配曲线如图2所示，其界限粒径d10、d30、d60分别为0.21 mm、0.43 mm 和1.29 mm，平均粒径d50为0.81 mm，不均匀系数Cu为6.14。为保证试验地基的密实度和均匀性，往模型箱内填筑时采用分层压实填筑。试验砂的最大和最小干密度分别为1.951 g/cm3和1.523 g/cm3，通过分层压实后，试验地基土的密度为1.681 g/cm3，此时地基土的相对密实度为0.428，属于中密砂。为保证每次试验时地基的密实度和均匀性，往模型箱内填筑时采用砂雨法进行分层压实填筑，通过控制每层砂土的密度来控制整体的密实度。试验用砂的主要性质参数如表1所示。

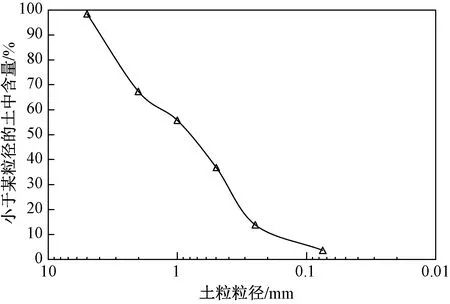
图2 模型土粒径分布曲线

表1 模型土基本物理参数

2 模型试验结果

对不同埋置长度h下的斜撑承载试验的位移和轴向压力进行处理后，得到斜撑承载的荷载-位移曲线如图3所示。斜撑在进行加载试验前即受到来自于上部楔形加载块的重力，这部分荷载转换为斜撑的轴向压力为61.25 kPa，因此曲线起点不处于坐标原点。

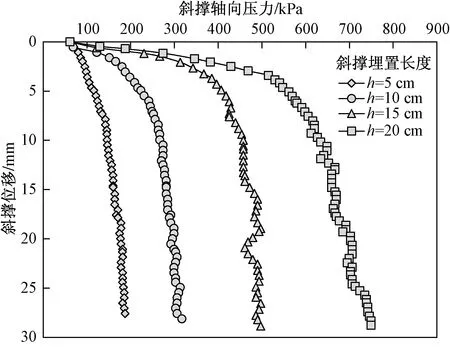
图3 斜撑承载荷载-位移曲线

从图3可以看出，随着斜撑埋置长度的增加，在相同位移时所对应的轴向荷载逐渐增大，说明斜撑的承载能力逐渐提高。参考《建筑基桩检测技术规范》(JGJ 106—2014)中单桩竖向抗压静载试验的单桩极限承载力确定方法，本试验中的荷载-位移曲线属于陡降型，故应取其发生明显陡降的起始点对应的荷载值为极限承载力Pu。对应于不同斜撑刺入深度的斜撑极限承载力分别如下：斜撑埋置长度5 cm时，Pu=127.62 kPa，对应的斜撑轴向位移L=6.46 mm；斜撑埋置长度10 cm时，Pu=241.41 kPa，对应的斜撑位移L=6.01 mm；斜撑埋置长度15 cm时，Pu=425.17 kPa，对应的斜撑位移L=8.21 mm；斜撑埋置长度20 cm时，Pu=605.32 kPa，对应的斜撑位移L=9.26 mm。可以看出，随着斜撑埋置长度的增加，极限承载力逐渐增大，每增加1倍钢管直径的初始埋置长度，斜撑的承载力分别增大了113.79、183.76、180.15 kPa。初步分析承载力增大的原因来源于两方面：一是由于埋置长度的增加，斜撑与地基土的接触面积增大；斜撑所受的侧摩阻力增大，二是由于更深的地基土能为斜撑提供更大的端阻力。

图4为不同埋置深度下斜撑达到极限承载能力时地基土破坏情况。斜撑达到极限承载能力时地基破坏形式为地表隆起开裂破坏，在斜撑埋置长度较浅时，结束加载时的地基土表面隆起较高，地表开裂现象比较明显，裂纹的宽度较大。斜撑埋置长度1倍管径时，地表最大隆起量达16 mm，最大裂纹宽度为8 mm；随着斜撑埋置长度的加大，地基土表面的隆起和开裂破坏现象则越来越轻微，斜撑埋置长度4倍管径时，地表仅出现轻微隆起，且地表处开裂的中心位置也距离斜撑刺入处最远，但地表的隆起范围较前者有所扩大。

3 数值模拟

3.1 计算模型及参数

为了进一步从土体内部变形及端阻力发挥情况等方面分析斜撑撑脚地基破坏模式，利用FLAC3D建立了斜撑承载试验的数值模型。数值模型的尺寸均与上节物理模型一致，考虑到模型的对称性，取1/2进行建模如图5所示。

模型试验中的斜撑模型采用的是304不锈钢材质，可认为整个实验过程中斜撑钢管处于线弹性变形状态，故使用弹性本构模型进行模拟，斜撑钢管的相关模型参数如表2所示。地基土体选用摩尔库伦本构模型，参数如表3所示。为更准确反映钢制斜撑与地基土之间的接触和滑移作用，在斜撑与地基土之间建立接触面单元进行模拟(图5)。地基土和接触面的相关参数取值应根据室内模型试验所得数据进行反推得到，如表4所示。数值模型采用逐级加载方式计算，在斜撑的上表面施加均布法向压力，在该级荷载作用时计算平衡后，读取该级荷载作用下的斜撑轴向位移，最终绘制斜撑承载数值模拟获得的荷载-位移曲线。

蓝色网格为斜撑部分

表2 钢管模型材料参数

表3 地基土体力学参数

表4 接触面单元力学参数

3.2 数值模拟结果及分析

图6为不同埋置长度斜撑模型试验结果与数值模拟结果的对比。图7为刺入长度为200 mm的斜撑在受到700 N和1 000 N轴向荷载作用时的轴力分布曲线。可以看出，除了斜撑埋置长度为1倍管径时数值模拟所得到荷载-位移曲线趋势存在一定差异外，数值计算结果与模型实验所得曲线吻合较好，可以认为此前所建立的模型和相关参数的取值是合理可靠的。利用数值模型计算能够得到斜撑承载过程中地基土的变形特征，可对室内模型试验结果进行有效解释。

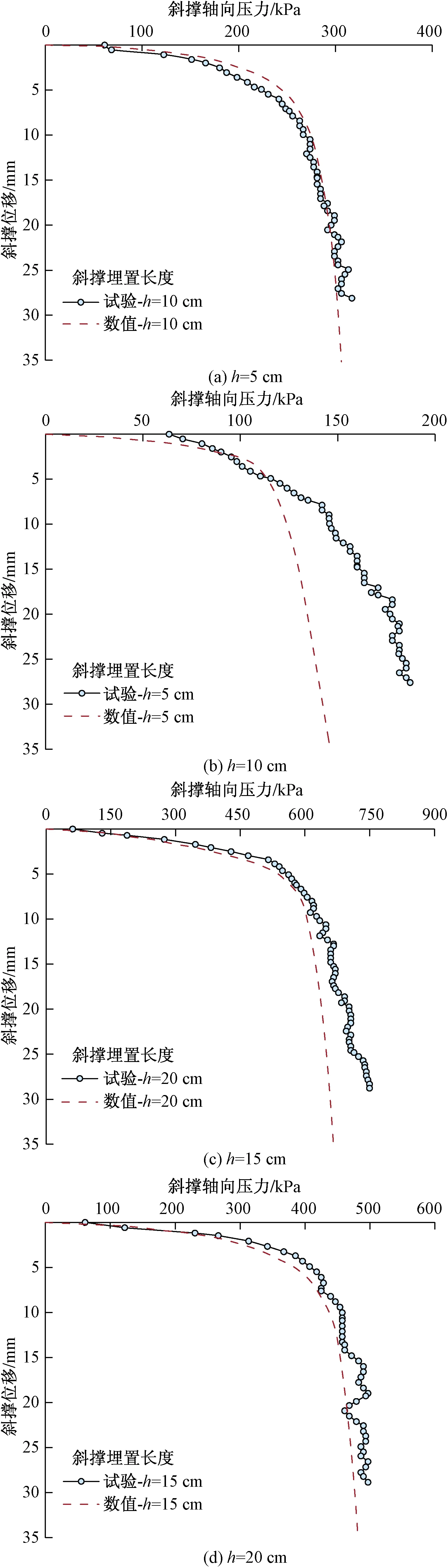
图6 数值模拟与模型试验的荷载-位移曲线对比

图7 数值模拟与模型试验的斜撑轴力对比

图8为不同斜撑埋深下地基土在破坏状态时的变形情况(非最终荷载阶段)。为便于对比分析，各模型均选取斜撑轴向位移约为10 mm时地基土的状态，此时斜撑的荷载-位移曲线已发生拐点，已经达到了极限承载能力，撑脚地基土均可认为达到其极限破坏状态。可以看出，位于斜撑端部附件地基土体受到斜撑轴向荷载的推力，将发生剪切破坏。斜撑端部的土体位移最大，随后位移向周围土体扩散，大小随着与斜撑端部的距离增加而不断衰减。因此，对于埋置长度较浅的斜撑[图8(a)和图8(b)]，由于地表距离斜撑底端距离小，斜撑的推力很容易让撑脚侧的土体达到被动土压力的极限平衡状态，从而形成贯通地表的连续滑动面；而对于埋置长度大于两倍管径的斜撑[图8(c)和图8(d)]，则难以形成贯通地表的连续滑动面，因此地表隆起量非常小；同时可以观察到随着斜撑的埋置长度增加，地表处的最大隆起位置也逐渐远离斜撑插入点的位置，这些规律都与室内模型试验相符合。

图8 不同撑脚长度下地基破坏状态的土体位移场

为分析埋置在地基内的斜撑在承载过程中荷载传递机理，对模型中斜撑承载时的斜撑轴力进行了监测。在斜撑埋入土体的部分等间距设置了5个监测点，读取各级荷载作用时每个监测点以下各节点沿斜撑轴线方向的承载力并进行累加，从而可得到斜撑在该点的轴力值，进而绘制沿斜撑埋置长度变化的轴力分布曲线，如图9所示。同时将斜撑顶面所作用的压力值乘以斜撑截面积即为斜撑的轴力值。斜撑顶部轴力减去某截面处的轴力值为该截面以上斜撑所受到的摩阻力之和，故斜撑底部的轴力值即为斜撑受到的端阻力值。从图9中可以看出，在荷载较小时，荷载主要由斜撑侧摩阻力承担，且摩阻力会随着荷载的增加而提高，而增加到一定荷载值后，由于斜撑位移较大，此时的摩阻力已完全发挥，至此摩阻力的大小将保持稳定，而端阻力的占比开始增大。随着斜撑的埋置长度增大，斜撑摩阻力和端阻力都不断增大，表明侧摩阻力和端阻力都将有所提升，这也与试验所得规律相符。

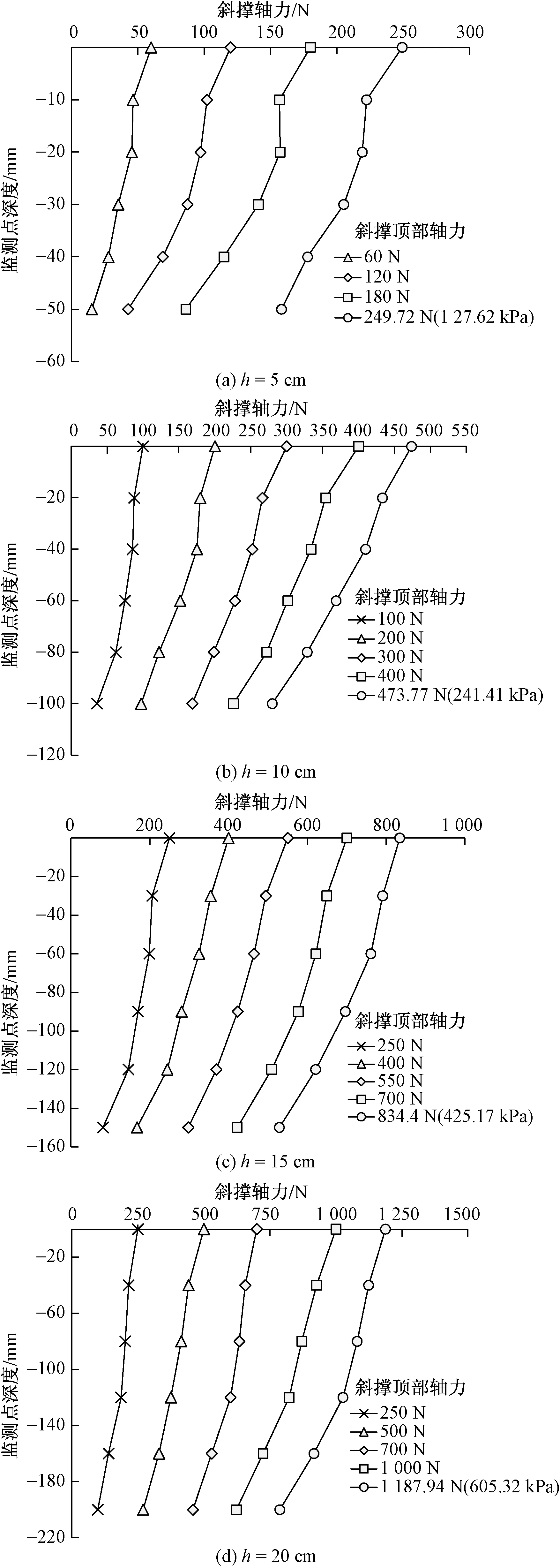
括号内数值为换算后的斜撑顶面处的轴力值；括号外数值为斜撑顶面所作用的均布压力

斜撑的端阻力占顶部荷载的比重变化曲线如图10所示。可以看出，在荷载较小时，荷载主要由斜撑侧摩阻力承担，端阻力的占比较小，而增加到一定荷载值后，端阻力的占比开始增大。可以看出，随着荷载的增大，端阻力所占比重越来越大，表明由斜撑端部土体所分担荷载比例越来越大。且端阻力所分担荷载比例随着斜撑的埋置长度增大而不断变大。在斜撑埋置长度为1倍管径时，端阻力最大占比约为50.95%；2倍管径时，约为59.05%；3倍管径，约为68.11%；4倍管径时，端阻力最大占比则达到了为72.2%。可见在本试验的地基土条件下，斜撑撑脚地基承载力主要来自于斜撑端部土体提供的端阻力。随着撑脚埋置深度的加大，撑脚端阻力的绝对值大小与所占相对比重均随之增加。

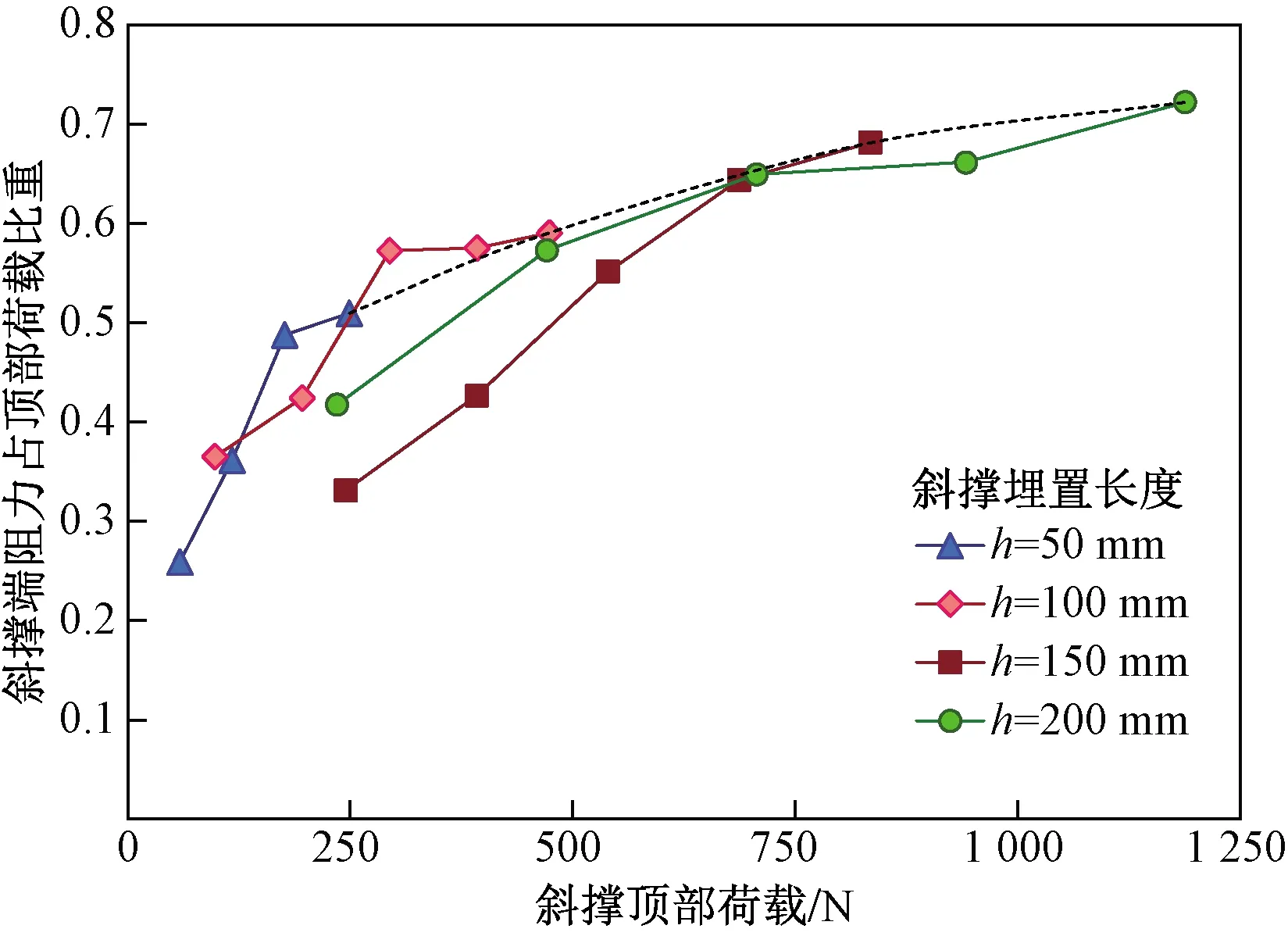
图10 端阻力占顶部荷载比重

4 承载机理及破坏模式

通过上述模型试验和数值模拟分析可以解释斜撑撑脚地基的荷载传递、承载机理以及破坏模式。在斜撑撑脚具有一定埋置深度的情况下，斜撑传递给地基的轴向推力将由撑脚侧面摩阻力qs和底端的端阻力qp两部分平衡，如图11(a)所示。

图11 斜撑撑脚稳定性的承载机理及破坏模式

当撑脚地基土体达到其极限承载能力时，侧摩阻力和端阻力均达到其极限值，此时端阻力将提供绝大部分的承载能力。但当斜撑撑脚埋置深度较浅时，撑脚一侧地基土体在斜撑推力的作用下将率先达到其抗剪强度τs，形成贯通地表的连续滑动面，此时撑脚的端阻力由浅层地基土体的被动土压力大小控制，故将远小于埋置深度较大情况下的端阻力。斜撑撑脚地基的极限承载能力因此将随着撑脚埋置深度的增加而增加；但当埋置深度大于一定长度时，由于端阻力发挥充分且侧阻力非主要抗力，极限承载能力将趋近其最大值。

5 结论

针对目前基坑抢险工程中经常使用的斜撑撑脚地基受力特点设计并制作了斜撑撑脚地基受荷的室内模型。对不同埋置深度的斜撑撑脚地基进行了加载试验，获得了荷载位移曲线和地基土变形特征。建立了能够考虑斜撑与地基土体相互作用的数值模型，通过对比模型试验结果验证了数值模型及相关参数的合理性。结合室内模型试验及数值模拟结果分析了斜撑撑脚地基的变形特征、承载机理及破坏模式。得到以下结论。

(1)斜撑地基的极限承载力由斜撑端阻力和侧摩阻力组成，其中端阻力占主要部分，在埋置深度较大的情况下达到承载力70%以上。

(2)斜撑撑脚埋置深度较浅时，撑脚的端阻力由浅层地基土体的被动土压力决定，因此会远小于埋置深度较大情况下的端阻力。

(3)当撑脚埋置大于一定深度时，由于端阻力发挥充分且侧阻力非主要抗力，极限承载能力将逐渐趋近其最大值。

(4)根据试验及数值分析揭示的成果，建议在实际工程应用中要确保斜撑撑脚有2倍管径以上的埋置深度，防止撑脚地基发生浅层被动土压力破坏。