“引导教学”视角下一道高考题的剖析——以2021年高考数学北京卷第9题为例

李红云 伍春兰

(北京教育学院 100120)

高考评价体系明确了“立德树人、服务选才、引导教学”的核心功能，将考察内容确定为“核心价值、学科素养、关键能力、必备知识”[1]，如何以高考题“引导教学”，落实学科核心素养，值得探究. 以2021年普通高等学校招生全国统一考试(北京卷)数学(以下简称高考数学北京卷)第9题(表1)为例，分享我们的研究.

表1 2021年高考数学北京卷第9题

1 学生调研

在北京某两校高二和高三各一个班，就第9题进行调查.学生独立解决并写出简要过程，选择典型作答的学生进行访谈.通过调研了解学生的解决思路及困难，主要有三种解决思路：运算求解、图形分析与运算求解、图形的直观想象.

1.1 运算求解

解析几何问题的通性通法，即联立圆和直线的方程，消元整理得到含参数k和m的关于x的一元二次方程：

(k2+1)x2+2kmx+(m2-4)=0.

①

利用两点间的距离公式表示弦长，运算中借助韦达定理整理为关于k和m的表达式，根据题干条件“弦长的最小值为2”，分析弦长表达式得到m的值.

调研发现，选择该思路的学生，有的只列出联立方程，最多到写出方程①.学生的表现反映出其面对稍复杂解析几何问题的信心不足，另外也说明其数学运算的训练不够，特别是含参数运算的训练.针对只能想到运算求解且无法解决的学生，教师要关注学生数学运算的训练，另外要引导学生从几何图形进行分析.

1.2 图形分析与运算求解

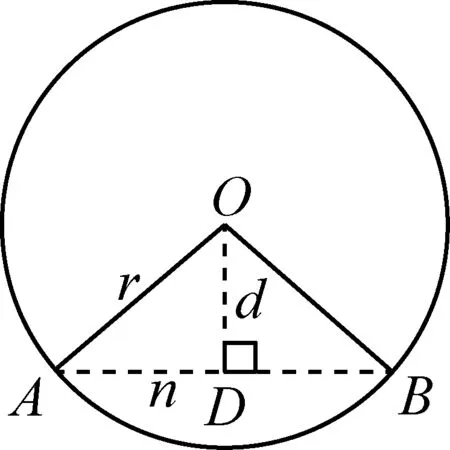
图1

借助弦心距求弦长的学生比较多，其中有的是开始想到联立方程求解，但是觉得计算很麻烦，转而借助弦心距求弦长.利用点到直线的距离公式表示出弦心距

②

进而表示出弦长

③

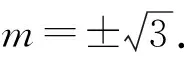
专家与新手解决问题的不同点在于，专家不是从目标往回走，而是扩展已有知识去解决问题，即想办法充分利用已有的条件[2].专家这种解决问题方式，对日常解题教学的启示是引导学生对题目的信息，包括“暗示”条件的有效读取、加工和转换.当解题遇阻，尝试等价转换是重要策略.波利亚怎样解题表的拟定计划中，多处提到转换问题，如“你能知道一道与它有关的题目吗？你能利用它吗？你能利用它的结果吗？你能利用它的方法吗？”特别地提到等价转换：“你能以不同的方式叙述它吗？”第9题将不同数学对象转换，即将弦长问题等价转换为弦心距问题，从而简化数学运算.

1.3 图形的直观想象

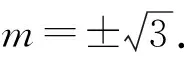
(1)无法想象弦长或弦心距的变化

当k变化时，学生能够想象出直线为过定点(0,m)的一直线族，并且能够顺利排除选项A和D.如果m=±2，过定点(0,±2)的直线族截得圆C的弦长最小值为0，因为k=0时，直线l与圆相切(图2)，可以排除选项A.

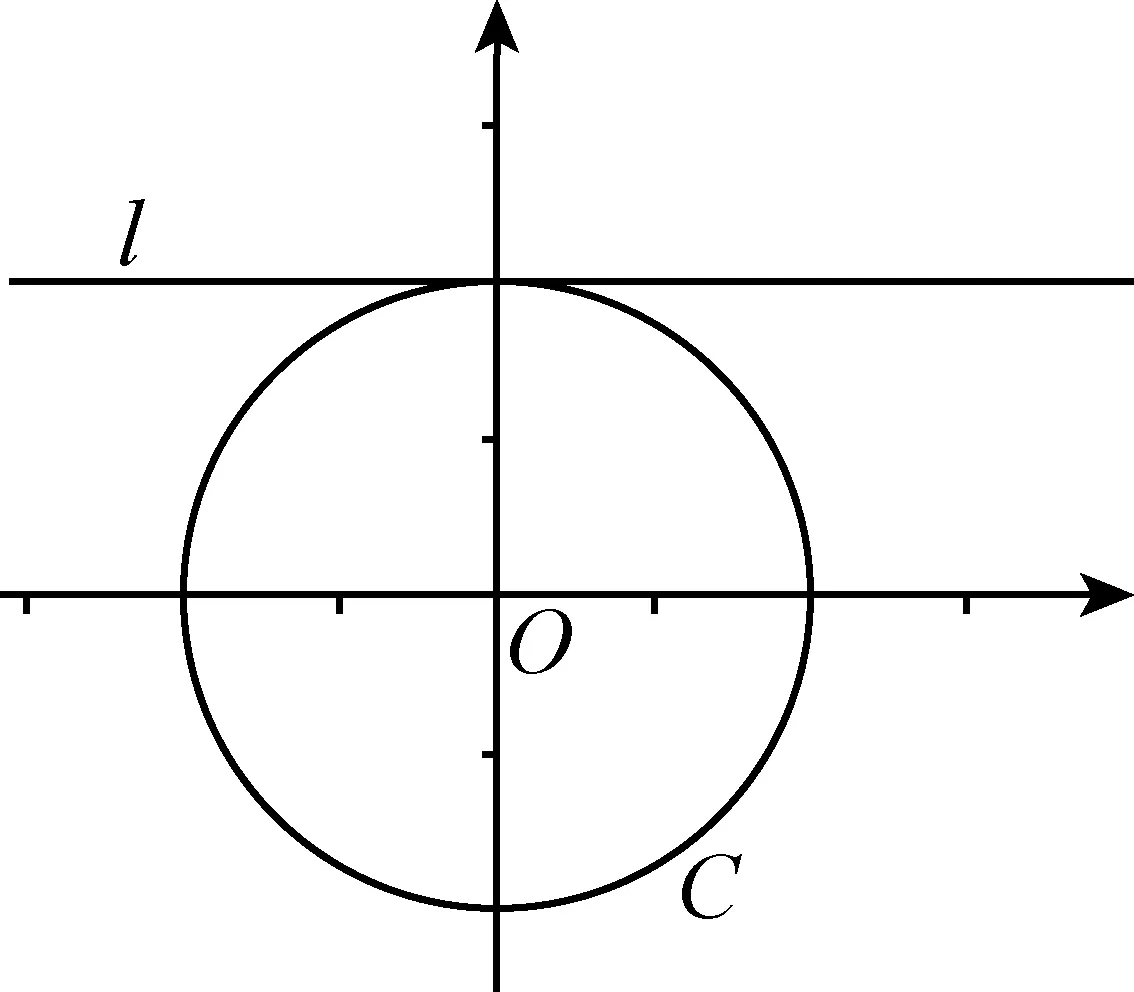
图2

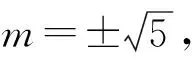
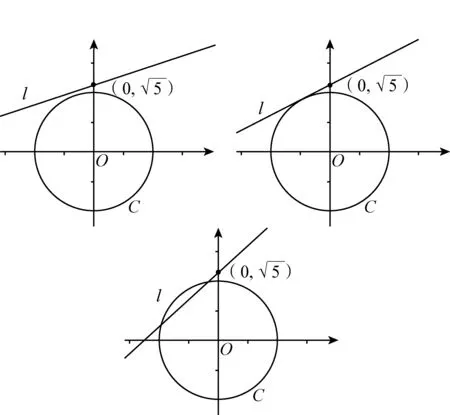
图3

无法进一步确定B或C，因为想象直线族截圆C的变化有困难，截得弦长如何变化的？何时弦长取得最小值？弦心距如何变化？弦心距何时取得最大值？即单个参数k变化，直观想象直线如何变化是容易的，直线变化所派生的圆C中弦长或弦心距如何变化是有困难的.

(2)猜想特殊位置，无法说明理由

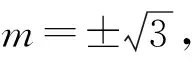
2 题目拓展

题目拓展的探究，需要跳出题目进行思考，题目有哪些条件？题目是否可以简化或变复杂？条件可以如何改变？条件改变后所考察侧重点是什么？等.

2.1 改变数值或表征

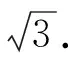
2.2 改变固定参数

由上述分析可知，m是定值这个隐藏条件，在题目解答中起着举足轻重的作用.若m不是定值，“弦长最小为2”简化为“弦长为定值2”，可否求得m的取值范围？这个改变引起问题结构的变化.

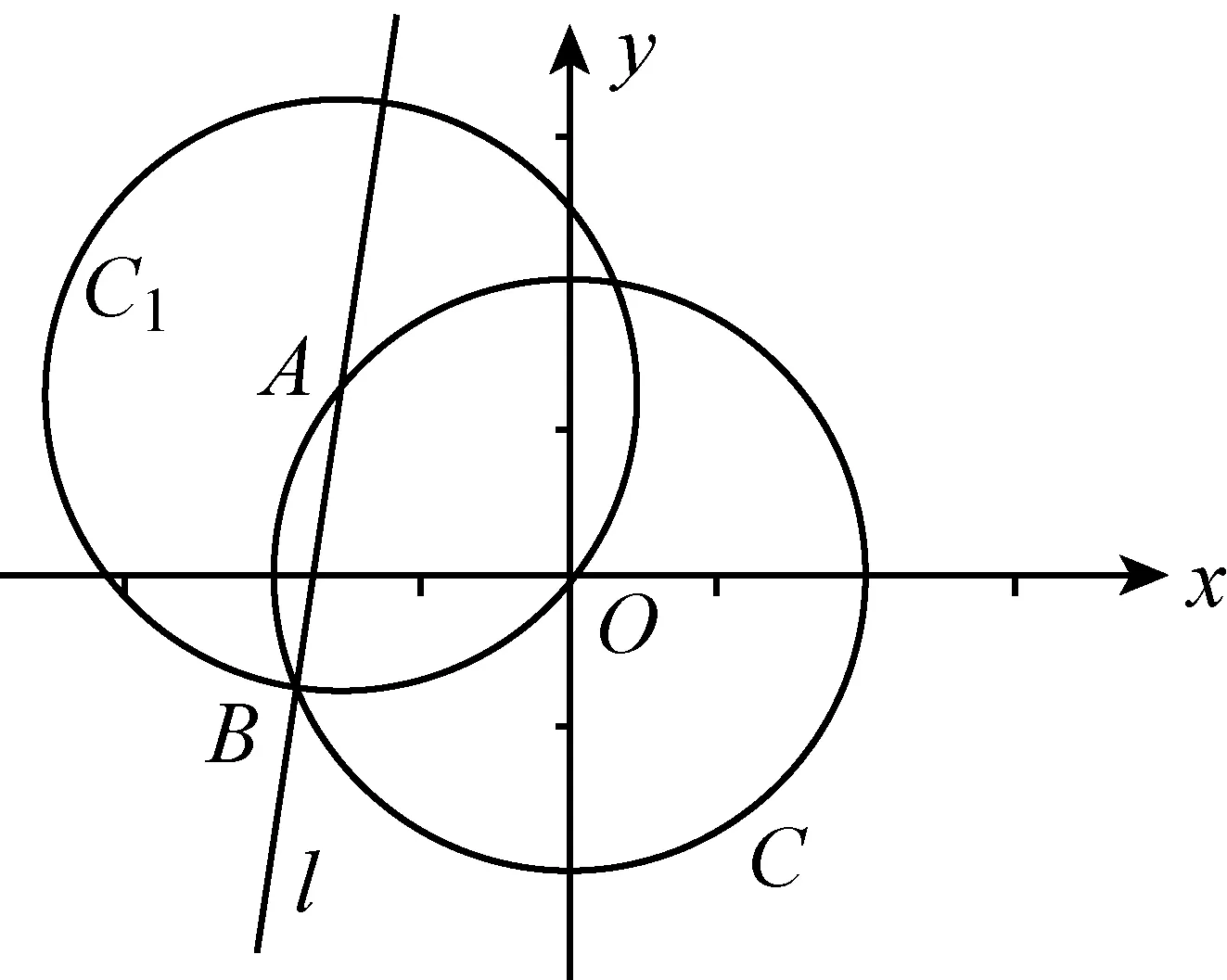
图4

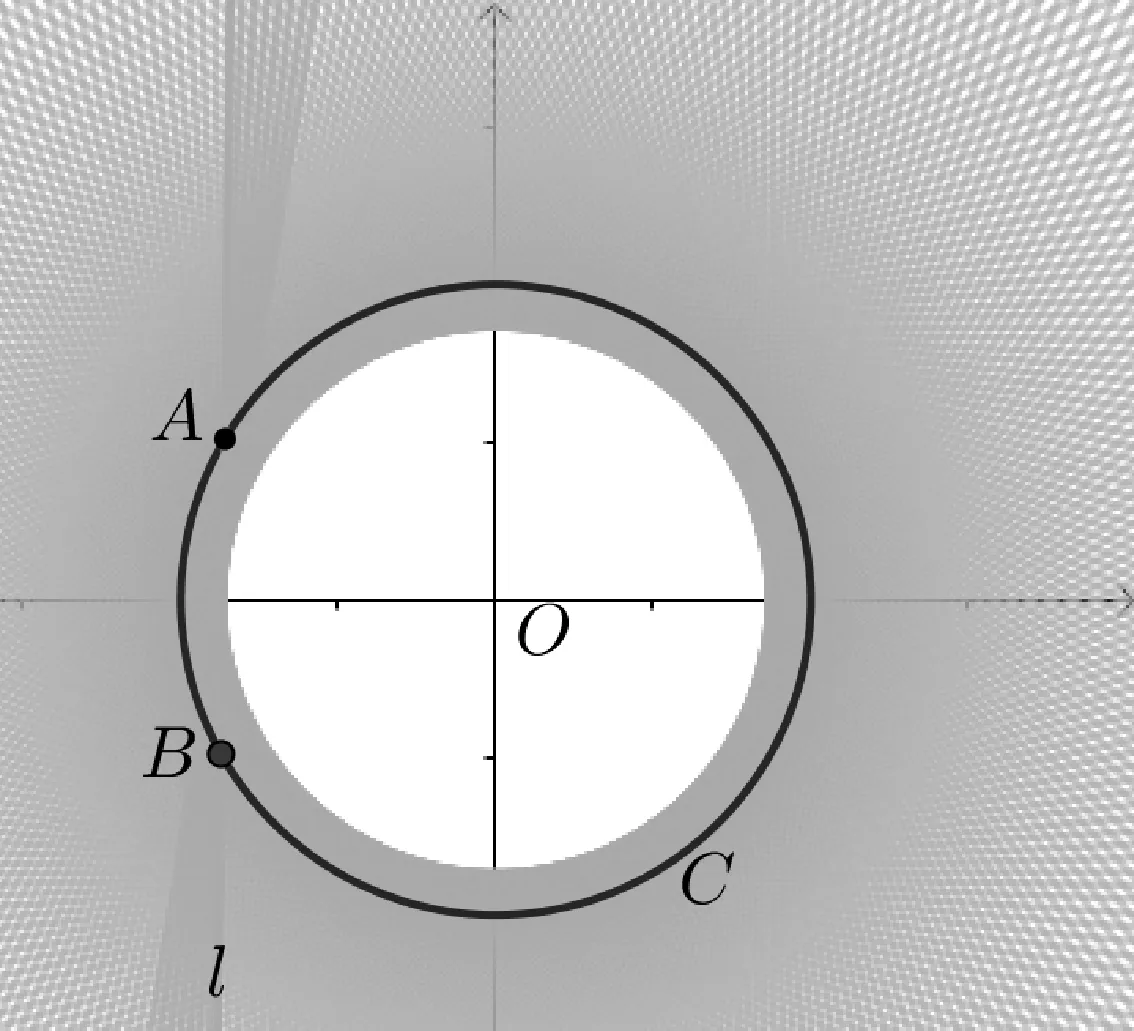
图5

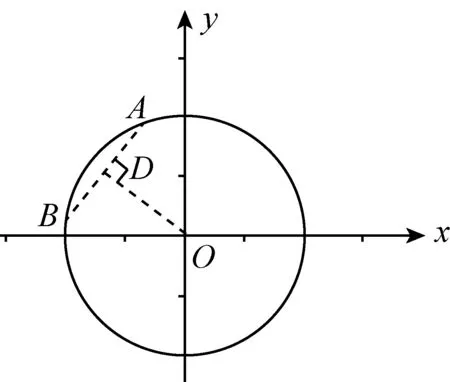
图6

由式②或③整理都可得

④

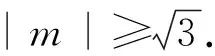
2.3 突破固定参数

将2.2中的“弦长为定值2”恢复到原题条件“弦长最小为2”.

依据2.2的探究，直线l:y=kx+m过小圆x2+y2=3上某点D.过点D的直线l与圆C相交的弦长范围为[2,4]，其中与小圆x2+y2=3相切时，弦长最小为2.当k变化且与小圆不相切时，此时容易观察或想象直线l与y轴可以相交在任意位置，即m可取任意值(图7).

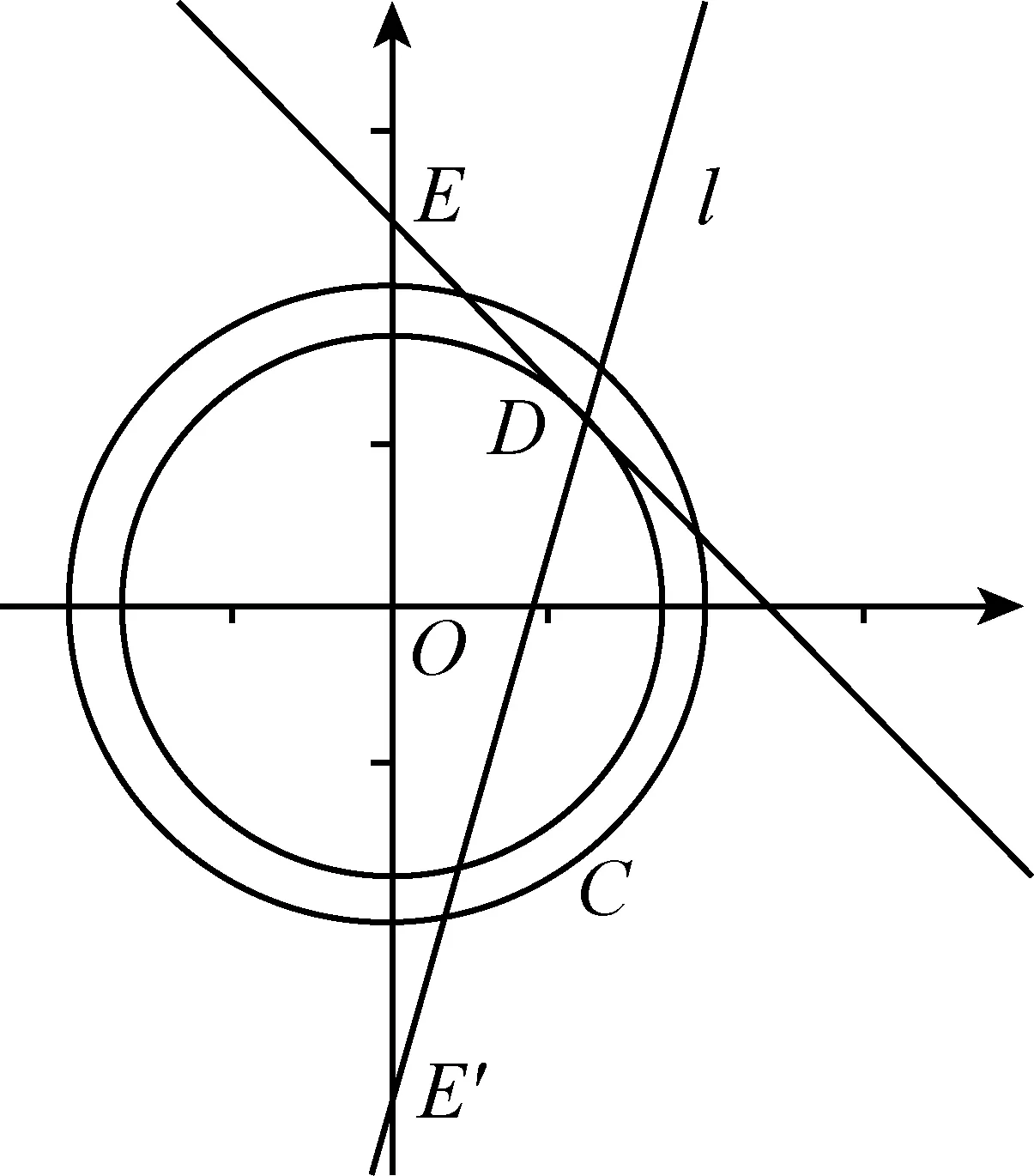
图7

⑤

⑤式中，k可以取到任意值，因此m可以取任意值.

因此，当弦长n最小值为2时，直线l一定过圆x2+y2=3上某个点，m可以取到任意值.

3 小结

3.1 学生研究

教师做学生研究，不仅仅是学生解题的表现，更为重要的是了解思维过程，正确解答学生的解题思路过程，错误解答的原因.如此才能找到帮助学生解决问题的对策.

与两个班级的执教教师交流过这个题目，都提到解决这个问题的思路主要是数形结合，调研发现学生表现与教师预期是有差异的，很多学生选择了通过运算方式解决，并且尝试联立方程表示弦长的学生都没有做出来.那么学生选择运算方式的原因是什么？没有做完的原因是运算能力问题，信心问题，还是时间不够？等，都是值得研究的.

3.2 解题回顾

解题是数学活动的基本形式和主要内容，解题在数学学习和教学中占比颇高，具有不可替代的作用.[4]波利亚在《怎样解题》中提出四步解题法：理解题目；拟定方案；执行方案；回顾.[5]解题后的回顾也是教学中容易忽略的环节.解题回顾，包括解决问题的经验是什么？是否充分理解题目条件？条件之间的关系？能否进行转化等？有没有其他解决思路？解决过程中遇到的困难？通过这个题目反映出自身数学知识和思考的哪些不足？等等.

调研中发现，通过运算解决问题的学生，并没有思考图形是什么样的，或者无法想象图形；通过直观图形解决的学生，有猜测对的，也有猜测错的，但是都没有再回到问题中反思结论是否正确.对于运算思路，要引导如何通过形的分析简化运算，从形的角度思考k=0在图形角度是什么？为什么这个位置弦长取得最小值？对于通过直觉猜想的学生，教学中要引导学生反思的意识，分析得到结论的合理性等.

3.3 题目研究

数学题目的研究，也是数学教师必备的基本功之一.教师对题目进行探究，经历发现、提出、分析和解决问题的完整过程，也有利于培养学生发现问题、提出问题的能力.

通过对第9题的剖析，得到弦长n、斜率k及截距m三个参数之间的依赖关系.将其中的一个参数固定，可以使其成为高中生可求解的封闭题目，正如第9题利用选项支让m成为了定值.

题目拓展研究中，经历了小改动、中变化、更大拓展的过程.小改动是对原题条件数值或数学对象表征进行改变，有利于学生建立数学对象的联系，发展数学思维的灵活性.中变化是改变固定参数，参数k和m都是变化的，将“弦长最小值为2”退化为临界条件“弦长为2”，通过借助信息技术的动态变化，得到问题的解决思路.更大拓展则是三个参数都在变化，此时信息技术起到了支持数学思考的作用.

3.4 技术融入

调研发现学生对复杂图形的直观想象能力较弱.教学中可以借助信息技术的优势，帮助学生建立动态变化的直观表象，这是信息技术最基本的应用.当涉及多个参数变化不容易直观想象出图形的变化时，借助信息技术的探究成为了“雪中送炭”.教师通过信息技术的呈现，也可以激发学生兴趣，体验图形动态变化所带来的魅力，积累动态直观想象的经验，从而达到不畏惧动态变化的问题.

师生借由信息技术分析、解决问题，继而发现、提出、分析和解决新问题，是教师专业成长和学生思维发展的一条可行路径.