三次样条插值及其在第一类积分方程求解中的应用

唐锦萍

(黑龙江大学 数据科学与技术学院，哈尔滨150080)

1 引 言

在实际问题中，有很多数学物理问题的求解，都可以归结为如下形式的第一类Fredholm积分方程的求解问题：

(1)

其中，A(x，y)，g(y)假定为连续有界函数，f(x)为待求解的未知函数.方程(1)的求解，积分方程的离散是关键.根据离散方式的不同，积分方程的离散策略可以分为两类，一类是采用数值积分公式，如复化梯形公式等，直接在离散节点上对方程(1)进行离散[1]；另一类是先对区间分段，并给出未知函数f(x)的逼近函数，如分段Hermit插值函数，由于每个区间上逼近函数的解析形式是给定的，因此(1)式左端的积分在每一个小区间上可以被解析的计算出来，进而将所有区间上的积分整合到一起，就可以得到方程(1)的离散形式[2].本文将采用第二类离散方式，利用三次样条插值函数近似f(x).三次样条函数具有分段、低阶、光顺的特性，经常被用来作为光滑函数的近似[3-4].

由于第一类Fredholm积分方程的求解通常是不适定的，因此常采用正则化策略来克服，进而得到稳定的数值解.注意到在以往的利用三次样条函数进行积分方程离散的文献中[5]，作者一般采用的是先正则化后离散的方式.这种方式先将积分方程的求解转化为带约束的优化问题：约束条件就是积分方程(1)，优化目标是一个极小化泛函，通常可以为未知函数f(x)的L2范数，或者其一阶导数f′(x)、二阶导数f″(x)的L2范数，其中后两种优化目标能起到光滑化的作用.然后将带约束的优化问题转化成无约束优化问题，并用三次样条函数离散，这样就得到了关于未知函数在离散节点上的函数值的线性方程组.该线性方程组的解通常是存在的，且其解是稳定的.与先正则化后离散的策略不同，本文将采用先离散后正则化的思路进行求解，先对f(x)利用三次样条函数进行插值逼近，得到方程(1)的离散化线性方程组的形式后[6]，通过引入未知解的离散化光滑条件，将方程(1)的求解转化为求解关于线性方程组的带约束优化问题.为得到方程(1)的稳定数值解，本文采用了多重离散化光滑条件，所采用的方法更直观、灵活.具体的理论方法见本文的第2部分和第3部分，第4部分的数值模拟验证本文所采用方法的可行性和有效性.

2 积分方程的离散化

下面将利用三次样条插值函数对积分方程(1)进行离散.首先，将积分区间[a，b]进行等距剖分成n段，步长为h，每一个分点xi=a+ih，i=0，1，…，n，相应地yj=a+jh，j=0，1，…，n，则在整个区间[a，b]上，积分方程(1)可以写成如下形式

下面对未知函数f(x)应用三次样条插值函数S(x)进行逼近，由于S(x)∈C2[a，b]，于是可设S(x)在xi处的一阶导数值为mi，即S′(xi)=mi.在小区间[xi，xi+1]上，S(x)是一个不高于三次的多项式，记S(x)在区间[xi，xi+1]上的表达式为S3(x)，于是有

S3(xi)=f(xi)，S3(xi+1)=f(xi+1);S′3(xi)=mi，S′3(xi+1)=mi+1.

实际上，S3(x)为满足以上条件的一个三次Hermit插值，则根据Hermit插值的形式得

S3(x)=hi(x)fi+hi+1fi+1+Hi(x)mi+Hi+1(x)mi+1，

(2)

其中，fi和fi+1分别为f(x)在xi和xi+1上函数值，hi(x)，hi+1(x)，Hi(x)，Hi+1(x)分别为三次Hermit插值的基函数，形式为

hi(x)=(h+2(x-xi))(x-xi+1)2/h3，hi+1(x)=(h+2(x-xi+1))(x-xi)2/h3，

将S3(x)的表达式(2)带入方程(1)中可得

(3)

其中

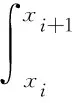
将方程(3)写成如下的矩阵向量的形式：

H(f0，f1，…，fn)T+H*(m0，m1，…，mn)T=(g0，g1，…，gn)T.

(4)

由S″(x)的表达式，可得

2m0+m1=3f(x0，x1)-h1M0/2，mn-1+2mn=3f(xn-1，xn)+hnMn/2，

其中f(x0，x1)表示x0，x1两点处的一阶差商，f(xn-1，xn)表示xn-1，xn两点处的一阶差商.当M0，Mn值都为0时，称为自然边界条件，适合自然边界条件的样条称为自然样条.此时，方程(3)可以写为

(5)

其中

将λi，μi带入式(5)，并将差分格式f(xi-1，xi)展开，有

B(m0，m1，…，mn)T=K(f0，f1，…，fn)T，

(6)

其中

则

(m0，m1，…，mn)T=B-1K(f0，f1，…，fn)T，

将上式代入到式(4)，有

(H+H*B-1K)(f0，f1，…，fn)T=(g0，g1，…，gn)T.

(7)

不妨将(7)式简记为

Af=g，

(8)

其中A=(H+H*B-1K)，f=(f0，f1，…，fn)T，g=(g0，g1，…，gn)T.方程(8)就是具有二阶连续导数的积分方程的数值求解模型，不难发现，这是一类第一类算子方程.求解(8)式就可以得到积分方程(1)的近似解.

3 正则化策略

由于第一类Fredholm积分方程的不适定性，导致其离散化后得到的线性方程组(8)的解在Hadarm意义下是不适定的，因此为了得到方程(8)的适定解，一般采用Tikhonov正则化策略，即将对(8)的求解转化成如下的无约束极小化问题

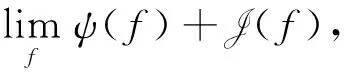
(9)

(10)

也可以采用单一罚项的约束.本文将在下一节对不同约束进行对比.对公式(10)右端的三项采用离散近似，即

并将近似表达式带入到(9)中，则重构出来的光滑解实际上就是使下式达到最小值的f

(11)

其中λ1，λ2，λ3是三个正则化参数.对(11)中的目标泛函关于f求极小，并用矩阵形式表示，则有

AT(Af-g)+λ0H0f+λ1H1f+λ2H2f=0，

(12)

其中H0就是单位阵，Hi，i=1，2为加入的1阶和2阶导数约束所对应的光滑矩阵，其形式分别如下：

求解方程(12)，整理可得

f=(ATA+λ0H0+λ1H1+λ2H2)-1ATg，

即为积分方程(1)的数值近似解.

4 数值模拟计算

通过数值模拟来检验本文提出的方法的可行性与稳定性.首先生成数据，即先给定积分方程的精确的解析形式f(x)，并计算出积分方程的右端函数g(y)，及其在不同的离散点上的值g(yi)，i=1，…，n.值得指出的是，本文中主要考虑精确解是光滑连续函数的情形.适当地对数据加入人为的干扰误差，以模拟实际数据中的测量误差.在下面的例子中，对g(yi)加入了0～1%的高斯白噪声.

以相对误差RE=(‖f*-f‖)/‖f‖，和残差RESIE=‖Af*-g‖为评价指标，对比了多重约束与单一约束对重构解的不同影响.同时，由于算法中有三个不同的正则化参数，为了找出最优的参数，首先经验地给出H2前的正则化参数λ2，在此基础上，对H0和H1前面的参数设计了循环遍历算法，以找出能使相对误差达到极小的参数组合.

例1真解f(x)=sin(x)，核函数A(x，y)=exy，x∈[1，2]，不同约束条件下的重构结果见图1所示，其中单独约束的情况正则化参数均为0.005，剖分的节点总数n=30. 混合约束中，二阶导数H2前面的正则化参数为0.005，在此基础上，对0阶导数和1阶导数前面的正则参数各循环遍历10次，参数遍历的范围为初值为0.5，公比为0.1的等比数列.根据这100种(λ0，λ1，λ2)的组合，可以得到相应的重构解，并可以计算每一种重构解的相对误差.选择相对误差最小的，对应的组合为

λ0=5×10-6，λ1=5×10-8，λ2=0.005.

根据图1，不难看出混合约束的重构效果是最好的，精确解与重构解几乎是重合的.在采用单独约束的方法中，二阶导数由于具有较强的光滑性，因此其重构效果相较图1(c)和图1(d)要好.为了更好地量化对比的结果，列出了不同方法下重构解的相对误差和残差，见表1.通过表1，可以看出多重约束方法具有最低的相对误差，这也说明了采用多重约束确实能提高重构解的精度.

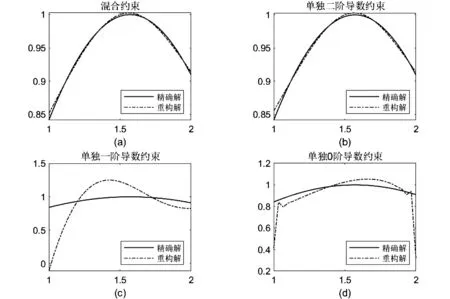
图1 不同约束下精确解与重构解的对比

表1 不同约束下重构解的相对误差和残差

例2真解f(x)=sin(5x)，核函数A(x，y)=exy，x∈[1，2]，通过例1可以发现混合约束与二阶导数约束的重构均优于一阶导数约束和0阶导数约束.本例中仅对比混合约束与二阶导数约束，结果见图2(a)，其中二阶导数约束前面的正则化参数为0.005，混合约束的正则化参数组合为λ0=5×10-6，λ1=5×10-6，λ2=0.005.两种罚项约束下得到的相对误差和残差见表2的第二行.

表2 例2和例3不同精确解下重构解的相对误差和残差

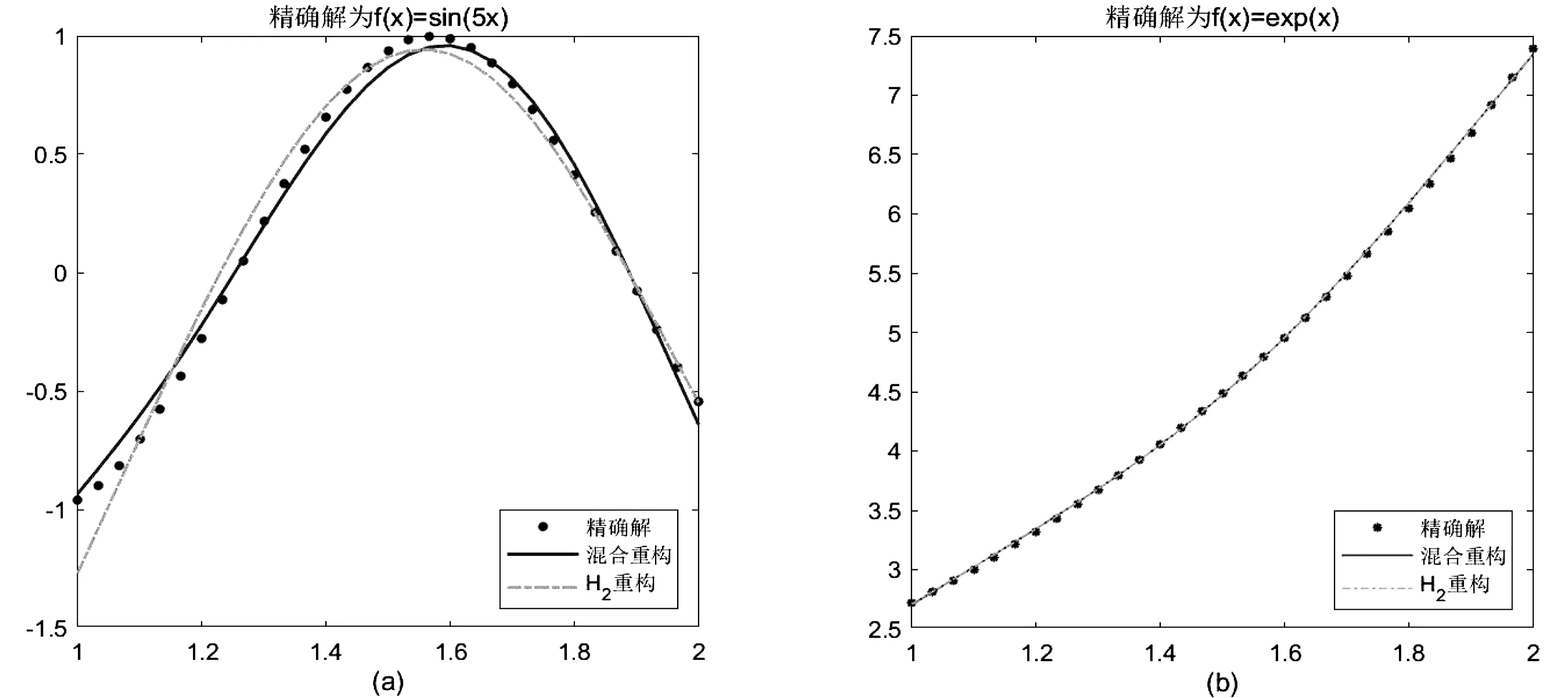
图2 例2和例3的重构结果

例3真解f(x)=ex，核函数同上.仍然对比混合约束与二阶导数约束的重构效果.结果见图2-(b)，其中二阶导数约束前面的正则化参数为0.005，混合约束的正则化参数组合为λ0=5×10-7，λ1=5×10-8，λ2=0.005.两种罚项约束下得到的相对误差和残差见表2的第三行.

通过例2和例3，可以发现，当精确解在重构区间上，满足单调性时，如例3，多重光滑约束和二阶导数约束的结果几乎无异，甚至二阶导数的误差量化结果要优于多重光滑约束；但当精确解在重构区间上，虽然连续光滑，但不满足单调性时，如例2，则多重光滑约束的重构效果要优于二阶导数约束，特别是在相对误差的量化上，多重光滑约束的相对误差几乎是二阶导数约束相对误差的2倍.

5 结 论

本文利用三次样条插值函数对积分方程进行离散，并对离散得到的线性方程组采用光滑约束，以得到稳定解.得到结论如下：

(i) 当精确解的光滑性较高时，采用三次样条函数对其进行近似符合对解的光滑性的要求，且方法简单易行，转化成无约束问题后直接求极小解线性方程组即可，不用进行迭代求解；

(ii) 当精确解的光滑性较高，且满足一定的单调性时，采用多重光滑约束可以得到精度较高的重构解；

(iii) 方法中的正则化参数的选取，要视对解的要求而定，针对不同要求，选取不同的光滑参数，如果解的光滑性要求较高，则应以高阶导数约束为主，适当减小其他低阶导数约束前面的正则化参数.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.