微分在代数证明中的两个应用

申 静， 刘 欢

(1.河南工业大学 理学院，郑州450001； 2.郑州大学 数学与统计学院，郑州450001)

1 引 言

数域P上n阶方阵A的特征值λ0是其特征多项式|λE-A|的根，根的重数是特征值λ0的代数重数，而几何重数是属于该特征值λ0的特征子空间Vλ0={x∈Pn|Ax=λ0x}的维数.几何重数小于等于代数重数是线性代数的一个结论，在判断矩阵是否与对角矩阵相似这一问题上发挥着重要作用.众所周知，数域P上n阶方阵A相似于对角矩阵的一个充要条件是A的所有特征子空间的维数之和等于n[1].考虑到代数重数和几何重数的关系，充要条件可换为A在数域P上有n个特征值，且所有特征值的代数重数和几何重数对应相等[2].换言之，如果A的某一特征值的代数重数不等于几何重数，则A不与任何对角矩阵相似，不必验证所有特征值的几何重数之和是否等于n，这样就大大减少了计算量.因此，证明几何重数小于等于代数重数显得尤为重要.与现有的证明思路不同，本文不再是单纯的利用线性代数知识，而是结合行列式函数的微分，给出一个新的证明过程.此外，本文通过构造辅助函数，并利用微分证明一个关于线性变换和向量积的恒等式.

2 主要结果和证明

2.1 基础知识

引理1[1]设α1(λ)，α2(λ)，…，αn(λ)是数域P上关于λ的n维列向量函数，则

引理2设数域P上n阶方阵A的特征多项式为f(λ)=|λE-A|，将λE-A按照列分块为

λE-A=(β1(λ)，β2(λ)，…，βn(λ))，

对任意的正整数m≤n，则

其中Λ={(x1，x2，…，xm)|1≤x1，x2，…，xm≤n，且是互不相等的整数}，ej表示n阶单位矩阵的第j列元素组成的列向量.

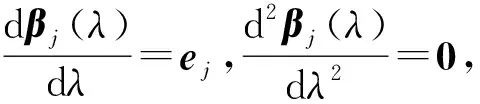
det(β1，…，βj1-1，ej1，βj1+1，…，βjm-1，ejm，βjm+1，…，βn)，

(j1，j2，…，jm)∈Λ的线性组合，且组合系数是一一映射{1，2，…，m}{j1，j2，…，jm}的个数m!.即证.

推论1特征多项式f(λ)的导数和主子式之间满足下述关系

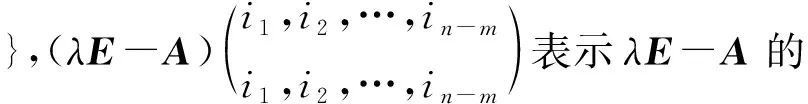
定义1对任意的u，v∈3，则向量积

其中e1，e2，e3是3的标准正交基.

2.2 应用案例一

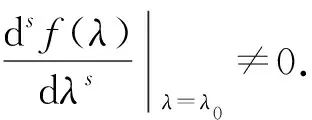
定理1设n阶方阵A的特征值λ0的几何重数为t，则s≥t.

证根据推论1和引理3可知

(1)

断言：λ0E-A至少有一个非零的n-s阶主子式.否则，n-s阶主子式全为0，与(1)式矛盾.根据矩阵秩的判定准则可知方阵λ0E-A的秩r≥n-s，从而可得特征值λ0的几何重数t=n-r≤n-(n-s)=s.即证.

下面给出判定代数重数等于几何重数的两个充分条件：

推论2n阶方阵A的特征值λ0的代数重数为1，则λ0的几何重数也为1.

证由于λ0为A的特征值，则|λ0E-A|=0，从而有rank(λ0E-A)0，再根据定理1可知t≤1.即证t=1.

推论3实对称矩阵的每一个特征值的代数重数等于几何重数.

2.3 应用案例二

定理2对任意的u，v∈3，A∈3×3，则

(Au)×v+u×(Av)=trace(A)(u×v)-AT(u×v).

(2)

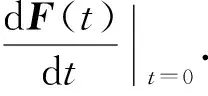
存在δ>0，对任意的|t|<δ，使得det(E+tA)>0.当|t|<δ时，令

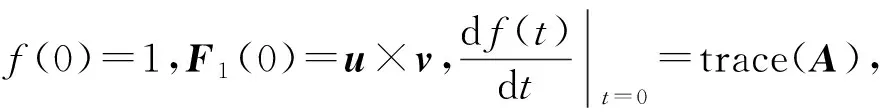
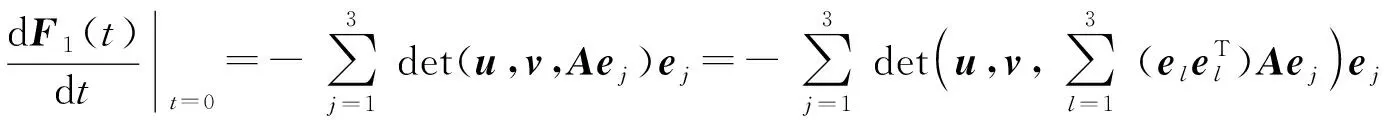
3 结 论

本文从微分的角度出发，证明了代数中的两个结论：矩阵的特征值的代数重数大于等于几何重数，关于线性变换和向量积的一个恒等式.本文给出了微分在代数中应用的两个案例，更多交叉应用的案例可以参见文献[3，4].

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.