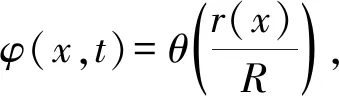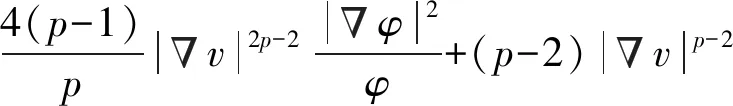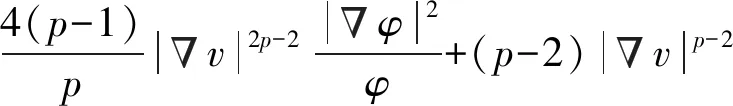一类非线性p-Laplace方程的Liouville定理
蒋群群,王林峰
(南通大学 理学院,江苏 南通 226019)
假设M是一个带度量g的n维完备流形。本文研究如下非线性p-Laplace方程
Δpu+aup-1lnu+λup-1=0,
(1)

如果p=2, 式(1)为
Δu+aulnu+λu=0。
(2)
文献[1]得到Ricci曲率为负下界的完备流形上正调和函数的一个最优微分不等式。λ为正时方程Δu+λu=0的微分不等式的证明方法类似于文献[1],也可参看文献[2]。文献[1]不等式中的等号能够取到,因此这个微分不等式是最优的,这也意味着著名的Yau的Liouville定理[3], 即在具有非负Ricci曲率的完备流形上不存在非常数正的调和函数。光滑度量测量空间上类似的最优微分不等式在文献[4]中被建立。
当a<0时,Ma[5]得到式(2)的正解的一个微分不等式,还通过观察式(2)与膨胀梯度Ricci孤立子之间的关系,说明该微分不等式最优。膨胀梯度Ricci孤立子由下式定义[6]
(3)
式中:f为势函数;a<0。Ma观察到如果f是式(3)的势函数,则对某个常数λ,u=e-f满足式 (2)。
注意式(2)也与Perelman的W函数有关。定义
式中
文献[7]证明在紧流形上λ可以由满足
4Δu+2ulnu+λu=0
的正光滑函数u取到。文献[6]利用这个最小化结果来排除紧致流形上非平凡收缩的梯度Ricci孤立子的存在性。在其他情况下W泛函的研究可以参看文献[8-9]。由文献[7]可知,式(2)也与著名的Gross对数Sobolev不等式密切相关。
对p>1,Kotschwar等[10]在截面曲率有下界的假设下建立p-调和函数的局部微分不等式。由这个微分不等式能推出Liouville定理,该定理表明在截面曲率非负的完备流形上不存在非常数正的p-调和函数。Wang等[11]在截面曲率有下界的非紧流形上证明方程 Δpu+λup-1=0正解的一个最优微分不等式。与p-Laplace相关的Liouville定理的研究还可以参看文献[12-13]及其中的参考文献。
对于p>1和某个给定常数a,定义
式中
在紧致流形上能使λa,p取到的函数u满足Euler-Lagrange方程(1),式中λ=λa,p。关于p-Laplace方程的微分不等式已有不少研究[14-15]。本文将建立非线性p-Laplace方程(1)正解的微分不等式。
1 本文主要结果及预备知识
为方便起见,设
(4)
以及
(5)
下面结果是紧流形上的微分不等式。
定理1设M为Ricci曲率以-(n-1)K为下界的n维紧致流形,式中K≥0。假设u是式(1)的正解,令u=v,并且则
① 对a>0,如果p≥2,则
(6)
如果 1 (7) ② 对a<0,如果p≥2,则 (8) 如果1 (9) 定理1能推出如下Liouville定理。 定理2设M为Ricci曲率以-(n-1)K为下界的n维紧致流形,式中K≥0。假设u是a<0 时式(1)的正解。对p≥2,如果 (10) 流形非紧时也可以建立式(1)的微分不等式。引入截断函数时计算中包含距离函数的Hessian,所以假设截面曲率有下界[10]。 (11) 如果a<0,则 (12) 如第3章推论2所述,由定理3能得到关于截面曲率为负的非紧流形的Liouville定理。 up-1|lnu|≤C(p,δ)max{1,up-1+δ}≤C(p,δ)max{1,Mp-1+δ}, (13) 对给定的满足式(13)的函数v,定义算子L为 下面引理可以看作是Bochner公式的推广(见文献[17]式(2.5))。 (14) 式中 基于引理1可以推导出以下估计。 引理2设M为Ricci曲率以-(n-1)K为下界的n维完备非紧流形,式中K≥0。假设v=u是式(13)的解,则 (15) 证明由式(13)得 (16) 易知, (17) 把式(16)、(17)代入式(14),得 (18) 假设δ满足 (19) (20) 这里最后一个等式来自式(19)。因此式(20)在所有点都成立。由式(19), 从而得到式(15)。证毕。 注1式(4)中选择的是最优的,因为 在式(18)的条件下达到最大值。 本章证明定理1和定理2。 (21) 首先考虑a>0的情况。如果p≥2,容易看出 (22) 把式(22)代入式(21),得 因此,对任意x∈M, 从而得式(6)。 如果1 (23) 将式(23)代入式(21),并与p≥2的情况类似进行讨论,得到式(7)。 对a<0的情况,当p≥2时,将式(22)代入式(21),得 现在证明定理2。 在定理2中令p=2得到对式(2)的Liouville定理。 本章将利用截断函数给出非紧致流形上式(1)正解的微分不等式。由于计算涉及到距离函数的Hessian,需要假设截断曲率有下界。首先证明定理3。 定理3的证明设O∈M为定点,r(x)=dist(O,x)为由O决定的距离函数。对足够大的R>0,用B(O,R)表示中心为O半径为R的测地球。 考虑如下函数[15] 使得 (24) (25) (26) 在x0点,还有L(G)≤0。对任意σ∈(0,1),有 (27) 令 以及 假设δσ满足 与式(15)类似,有 由式(25)、(26)、 (27),以及在x0处L(G)≤0,得在x0处有 易见 及 由0≤φ≤1,得 (28) 式中Ci,i=1,2,3,…是依赖于n、p、σ、K、σ的常数。由1 (29) 首先考虑a>0的情形。易知 (30) (31) 将式(30)、(31)代入式(29),得 因此,对所有x∈B(O,R), 令R→∞,对所有x∈M, (32) 注意当σ1时,σ→,Aσ→A,在式(32)中令σ1,得 这个不等式意味着式(11),通过类似讨论可以得到式(12)。证毕。 推论2在具有非负截面曲率的n维非紧流形上,当a<0,且1

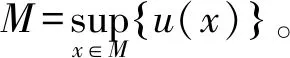
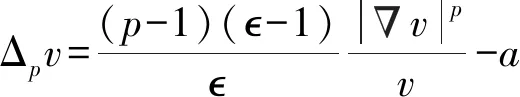







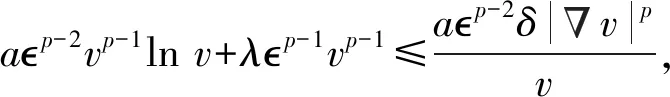




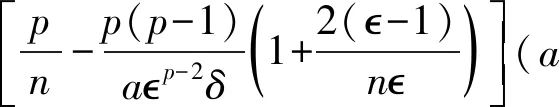
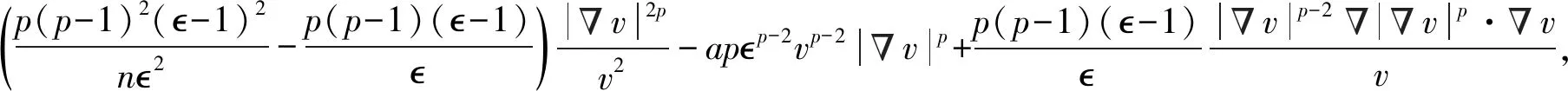

2 紧致流形


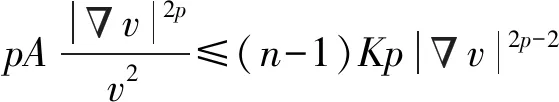


3 非紧流形