A General Framework to Construct High-order Unconditionally Structure-preserving Parametric Methods
Zhang Hong Liu Lele Qian Xu Song Songhe
(Department of Mathematics,National University of Defense Technology,Changsha 410073,China)
Abstract High-order accurate and stable explicit methods are powerful in solving differential equations efficiently.In this work,we propose a systematic framework to trade off accuracy for stability,especially the unconditional preservation of strong stability,positivity,range boundedness and contractivity.The whole algorithm consists of three steps:(1)Introducing a stabilizing term in the continuous system; (2)Integrating the system using an explicit exponential method; (3) Substituting the exponential functions with suitable approximations.We first show that a class of first-and second-order exponential time difference Runge-Kutta schemes are capable to preserve structures unconditionally when suitable stabilization parameter is chosen.Then by adopting the integrating factor approach with high-order Runge-Kutta and multi-step schemes as underlying schemes,three different approximation techniques are developed to make high-order schemes unconditionally structure-preserving,i.e.,(1) a Taylor polynomial approximation; (2) a recursive approximation; (3) an approximation using combinations of exponential and linear functions.The proposed parametric schemes can be deployed to stiff problems straightforwardly by treating the stiff linear term as an integrating factor.The resulting time integration methods retain the explicitness and convergence orders of underlying time-marching schemes,yet with unconditional preservation of structures.The proposed framework using the second and third approximations has relatively mild requirement on underlying schemes,i.e.,all coefficients are non-negative.Thus the parametric Runge-Kutta schemes can reach up to the fourth-order,and there is no order barrier in parametric multi-step schemes.The only free parameter-the stablization parameter in the framework can be determined a priori based on the forward Euler conditions.Unlike implicit methods,the parametric methodology allows for solving nonlinear problems stably and explicitly.As an alternative to conditionally structure-preserving methods,the proposed schemes are promising for the efficient computation of stiff and nonlinear problems.Numerical tests on benchmark problems with different stiffness are carried out to assess the performance of parametric methods.
Key words Strong stability Positivity Fixed-point-preserving Stabilization technique Parametric method
1 Introduction
Many scientific and engineering problems are modeled by differential equations that have essential constraints on solution components.For example,the diminishing of total variation in fluid dynamics[1],positivity of density and pressure[2],range boundedness of solution in hyperbolic equations[3,4],and maximum principle of order parameter in phase field models[5].As is well known,preserving these structures is not only important for solutions to be physically meaningful,but also relevant for the numerical stability of time integration methods.Consequently,many efforts have been devoted to the development of high-order accurate and efficient algorithms that can preserve such structures[5-13]To the best of our knowledge,few explicit methods can unconditionally guarantee these requirements.In this paper,we take a step towards high-order-accurate and highly-stable explicit schemes that can unconditionally preserve the above structures in specific settings.
Consider an initial value problem for a system of ordinary differential equations(ODEs)of type
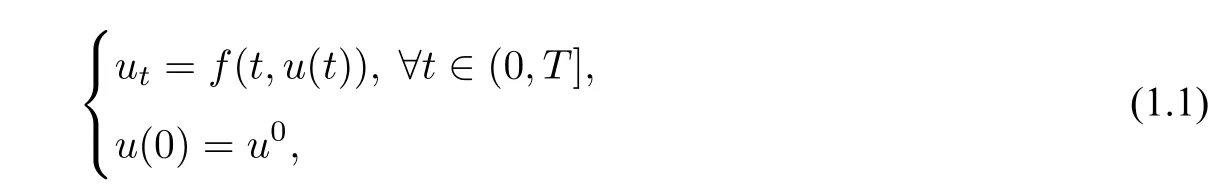
whereu0∈RN,f:R×RN →RNis a continuous function.We assume that the problem(1.1)has a unique solutionu:[0,T]→RN,and‖·‖:RN →R is a convex functional(e.g.,a norm,a seminorm,etc.):

We present definitions of several structures[14,15,16]relevant for the numerical stability of time integration methods for(1.1).
Definition 1.1(Strong stability preservation) Ans-step method is said to be strong-stabilitypreserving (SSP) with respect to the functional‖·‖if‖un+1‖ ≤maxi=1,···, s‖un+1-i‖,∀n ≥s-1 under the assumption that
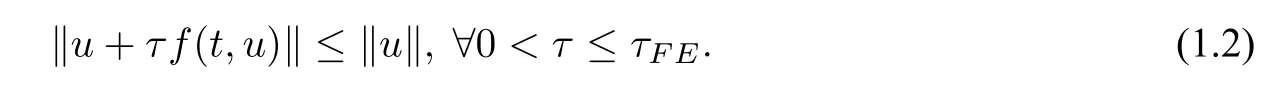
Definition 1.2(Positivity preservation) Ans-step method is said to be positive if,wheneverui ≥0,i=0,···,s-1,it guarantees thatun ≥0,n ≥sunder the assumption that
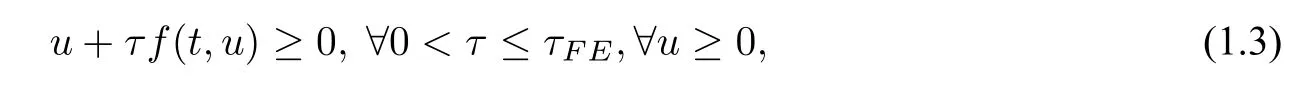
where the inequalities are element-wise.
Definition 1.3(Range boundedness preservation) Ans-step method is said to be range bounded in[m,M]if,wheneverm ≤ui ≤M,i=0,···,s-1,it guarantees thatm ≤un ≤M,n ≥s,under the assumption that

where the inequalities are element-wise.
Definition 1.4(Contractivity preservation) Ans-step method is said to be contractive if‖un+1-vn+1‖≤maxi=1,···,s‖un+1-i-vn+1-i‖,n ≥s-1,under assumption that

The research of Hundsdorfer et al.[17],Ferracina and Spijker[18,19],Higueras[20,21]and Gottlieb et al.[15] suggests that all these structures are strongly related.Consequently,they can be preserved using the same integration method in most situations.For convenience of presentation,we consider the preservation of strong stability in Definition 1.1 as an example.In the literature,the first scheme that can unconditionally preserve the strong stability is the implicit Euler formula(p.74 in[15]and[14,17,22]):
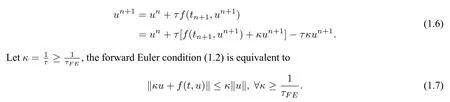
This so-called circle condition[14,15,22]means thatf(t,u)is bounded by a‘circle’measured by‖·‖that is centered at-κu ∈RNwith radiusκ‖u‖.It has been proven that such circle conditions are also necessary for the preservation of strong stability[14,15,23].By taking‖·‖on both sides of(1.6),we have
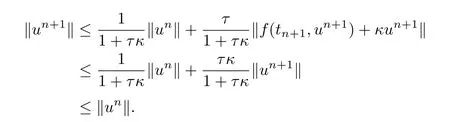
Although the implicit Euler method can preserve the strong stability without a time-step restriction,it is not surprising that high-order implicit Runge-Kutta(RK)or linear multi-step(MS)methods can not achieve this goal[17,22].Hence,significant efforts on the preservation of strong stability have been placed on developing methods that admit the largest possible SSP coefficientC,such that a method can preserve the strong stability under the condition 0<τ ≤CτF E.For research on conditionally SSP methods,we refer interested readers to[1,15,24-28]and references therein.
The unconditional strong-stability-preservation is a stringent,but very practical property,as it allows one to choose a time step as large as accuracy requirement permits.To obtain high-order unconditionally SSP methods,the diagonally split Runge-Kutta methods (DSRK) which were originally introduced to unconditionally preserve the contractivity[29,30],have been adopted to preserve the strong stability by Macdonald et al.[31].Unfortunately,it was shown that although second-and third-order unconditionally contractive DSRK methods do preserve the strong stability for all time-step sizes,they suffer from order reduction at large steps.By incorporating negative coefficients and downwind-biased spatial discretization,Ketcheson[32]developed a class of second-order RK methods with arbitrarily large SSP coefficient.Bonaventura and Della Rocca [16] proposed two unconditionally SSP extensions of the TR-BDF2 (trapezoidal rule-backward differentiation formula 2) method,based on a hybridization with the unconditionally SSP implicit Euler method that can be activated using a sensor detecting violations of relevant functional bounds.Very recently,by enforcing the backward derivative condition,Gottlieb et al.[33]proposed up to fourth-order unconditionally SSP implicit two-derivative RK methods.
In the spirit of developing explicit unconditionally SSP schemes,let us tackle the problem from another perspective.Consider adding anO(τ2)termτκ(un-un+1),instead of the zero termτκ(un+1-un+1) in (1.6),to the forward Euler formulaun+1=un+τf(tn,un).We construct a first-order implicit-explicit(IMEX)Euler scheme
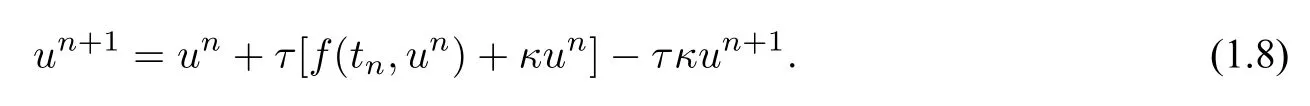

The stabilized system of scalar hyperbolic equations with stiff source terms was first introduced by Huang and Shu [4].Starting from traditionalpth-order integrating factor Runge-Kutta formulas,they proposed to replace exponential functions withpth-degree polynomial functions to weaken the exponential effects produced by the stabilization exponential term without destroying the convergence.Thus they obtained high-order bound-preserving modified exponential RK schemes that only require the time-step size to satisfy the forward Euler condition on the nonlinear term.In [13],Du et al.developed a Taylor polynomial approximation for stabilized integrating factor multi-step schemes.They constructed up to third-order conservative,and bound-preserving schemes for stiff multispecies detonation.Later,Du et al.[34,35] proposed up to third-order modified exponential RK schemes by using conservative approximations that were combinations of exponential and linear functions.Still,we have not seen the introduction of circle condition in the stabilization.
Meanwhile,as a variant of preserving the strong stability,the development of high-order unconditionally maximum-principle-preserving (MPP) schemes for Allen-Cahn-type (AC-type)semilinear parabolic equations in the form

where Ω∈Rdis an open,connected and bounded region with Lipschitz boundary∂Ω,has been a serious research objective in recent years.Du et al.[5]investigated two sufficient conditions,i.e.,
1.the linear operatorLis dissipative in the sense that if a functionwreaches it maximum onatx0∈Ω,then it must holdLw(x0)≤0.SuchLcould be the standard Laplace operator [36],nonlocal diffusion operator[37],or fractional Laplace operator[38],for example.
2.the nonlinear operatorNis assumed to act as a composite function,i.e.,N[w](x)=f(w(x))for any functionwandx ∈,wherefis a one-variable continuously differential function satisfying

for the abstract framework(1.9)to have a maximum principle:if the supremum norm‖·‖L∞of initial and boundary conditions are bounded byβ,then the solution will always satisfy‖u(t)‖L∞≤β,∀t >0.The above conditions imply the following lemmas that are important in deriving the maximum principle of AC-type equations,and developing MPP schemes.
Lemma 1.1([5]) The linear operatorLwith periodic or homogeneous Neumann boundary conditions generates a contraction semi-group{SL(t)=etL}t≥0with respect to the infinity norm‖·‖L∞on the subspace ofC().Moreover,forκ ≥0,letLκ:=L-κ,it holds that

where‖u‖L∞=
Lemma 1.2([5]) Assumeκ ≥max|ξ|≤β|f′(ξ)|.It holds that

for anyξ(x)∈C()with‖ξ‖L∞≤β.
Different from the development of SSP schemes,the circle condition (1.12) of AC-type equations has frequently been incorporated to develop high-order unconditionally MPP schemes.As demonstrated by Shen and Yang [39],as well as in earlier papers [40-45],a concise and effective technique for improving the stability of a numerical method is to add and subtract a linear term to the right-hand-side,e.g.,κ(u -u) for AC-type equations [39],the Douglas-Dupont regularizationκ(Δu -Δu) for the mean-curvature or Cahn-Hilliard equations [41,42,46].This stabilization technique is also known as explicit-implicit-null (EIN) method in [47].Such linearly stabilized schemes have been widely used to solve stiff equations.Tang and Yang [36] proposed the first unconditionally MPP scheme,in which the first-order implicit-explicit Euler scheme was combined with a stabilization technique.By using the energy factorization together with the stabilization approach,Wang and the coauthors[48,49]developed first-order semi-implicit schemes with small stabilization parameters to preserve the maximum principle unconditionally.However,traditional high-order temporal integrators fail to preserve the maximum principle unconditionally,because of lack of strategies in dealing with the stabilization term.By utilizing the exponential time difference methods and the stabilization technique,Du et al.[37] developed two unconditionally MPP exponential time difference (ETD) schemes for the non-local AC equation,i.e.,the stabilized first-order ETD1 scheme and the second-order ETD2 scheme.The ETD schemes have become popular in recent years.Du et al.[5] further proved that the ETD schemes can preserve the maximum-principle unconditionally for a class of semilinear parabolic equations.The success of the stabilized ETD schemes lies in the fact that the contraction property of the semi-group generated by the diffusion operator can be directly incorporated with the stabilization paramter in the temporal integrators,i.e.,The stabilization technique has also been introduced to the integrating factor Runge-Kutta(IFRK)framework.Li et al.[50]developed a first-order unconditionally MPP stabilized integrating factor Euler scheme.However,the strong exponential decay effect caused by the exponential components prevented it from being used in practical simulations.To weaken such an exponential decay effect,high-order schemes are preferable.Li et al.[51] proposed a class of up to third-order unconditionally MPP stabilized IFRK(sIFRK)schemes.The numerical experiments showed that the high-order sIFRK schemes greatly reduced the exponential decay.Nevertheless,the exponential effect is still a significant problem when facing large time-step sizes.
To remove the exponential effects,Zhang et al.[52]proposed to approximate exponential functions appeared in the sIFRK framework[50,51]using different Taylor polynomials.The resulting schemes can not only preserve the maximum-principle unconditionally,but also conserve the mass for conservative AC-type equations.However,because of the limitation of Taylor polynomial approximations,the obtained schemes can only reach third-order.In [53],Zhang et al.developed two arbitrarily high-order MPP parametric integrating factor multi-step (pIFMS) approaches to eliminate the exponential decay introduced by stabilized integrating factor multi-step methods,i.e.,a Taylor polynomial approximation and a combination of exponential and linear functions.Recently,a recursive approximation is introduced in[54]to develop up to fourth-order unconditionally structure-preserving parametric IFRK(pIFRK)schemes.The aforementioned approaches simplify the design of explicit,high-order accurate schemes,and bypass those typical challenges such as exponential effects and stability issues,to readily arrive at high-order unconditionally MPP single-and multi-step schemes.Moreover,they are capable to unconditionally preserve a wide range of structures.
The aim of this paper is to extend the stabilization techniqueκ(u-u)used in the IMEX Euler scheme(1.8),and the high-order approximations in[34,52,53,54],to the development of explicit,stable methods.Our goal is to increase the order and,at the same time,preserve structures in Definitions 1.1-1.4 without a time-step size restriction.Compared with the existing literature,new contributions of this work include:
· In Section 2.1.1,a series of up to second-order stabilized ETDRK schemes are proved to preserve the structures unconditionally.
· In Sections 2.1.2 and 2.1.3,three approximation techniques are proposed to develop unconditionally structure-preserving parametric RK schemes:(1)a Taylor polynomial approximation;(2)a recursive approximation;(3)an approximation using combinations of exponential and linear functions.
· In Section 2.2,arbitrarily high-order unconditionally structure-preserving parametric multi-step schemes are constructed using by different approximations,i.e.,a Taylor polynomial approximation,and a combination of exponential and linear functions.
· In Section 3,a series of explicit unconditionally structure-preserving schemes are developed for stiff,nonlinear systems.
· The unconditional structure-preservation of proposed schemes has relatively mild requirements on the stabilization parameter and underlying schemes,i.e.,stabilization parameterand all coefficients are non-negative.
· The proposed parametric schemes are explicit,free of limiters,cut-off post-processing and exponential effects.
The rest of this paper is organized as follows.In Section 2,we start with the preservation of structures by using a series of up to second-order stabilized exponential time difference RK schemes.Then,we consider a fixed-point-preserving improvement over the traditional integrating factor approach,and illustrate the main algorithms to construct high-order unconditionally structure-preserving single-step,and multi-step schemes.In Section 3,we consider a class of stiff,nonlinear systems,and illustrate the strategy of developing structure-preserving methods by incorporating proposed parametric schemes with integrating factors.In Section 4,some experiments are performed to demonstrate the effectiveness and advantages of the proposed schemes.Some concluding remarks are presented in Section 5.
2 Unconditionally structure-preserving parametric methods
To construct time integration methods for general nonlinear differential equations,three key design principles have been considered previously[55,56,57]:
1.Fixed points of the system are preserved.
2.The nonlinear term is handled simply and inexpensively.
3.The time-step size is selected to reflect the accuracy requirement,rather than restricted by stability requirement.
It is acknowledged that the more principles a numerical method can fulfill,the better is its applicability.In this section,we present a series of parametric methods that take care of the above principles,and are unconditionally structure-preserving.To avoid excessive introduction of symbols,we remark that some symbols have different meanings in different contexts.
2.1 Parametric Runge-Kutta-type schemes
2.1.1 Stabilized ETDRK schemes
For the exponential time difference integrators,the unconditionally structure-preserving framework consists of two steps.
Step 1By introducing a stabilization term-κu,κ >0 to the semi-discrete system(1.1),we obtain an equivalent system

To briefly illustrate the exponential time difference schemes,we introduce the functions[58]
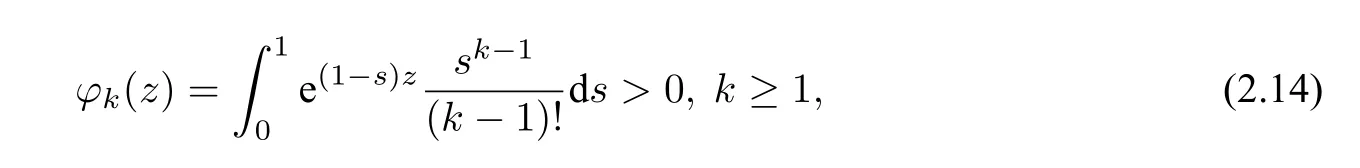
which satisfy the recursion
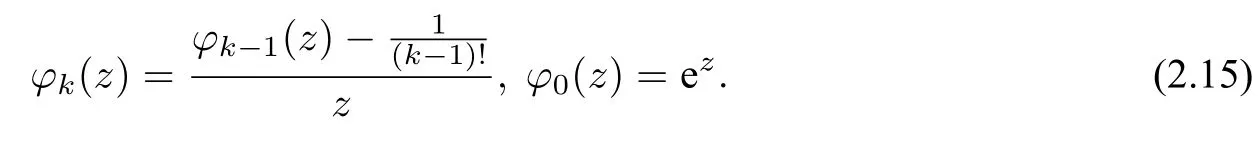
Consider some first-and second-order explicit ETDRK schemes[58,59]with Butcher-like tableaux

Step 2Lettn,j=tn+cjτ,by treating the nonlinear functionf(t,u)and linear termκuexplicitly,we outline the formulation of ETDRK schemes for(2.13)in the form

whereai,j(-τκ)are given by the Butcher tableau in(2.16).
The scheme with Butcher tableau(I)is known as the first-order ETD1 scheme[37].The ETD2[37]and RKMK2e[60]

are particular schemes in the second-order families of(II)and(III),respectively.It has been proven that ETD1 and ETD2 can unconditionally preserve the maximum-principle of(1.9)[5,37]under conditions in Lemmas 1.1 and 1.2.We present some preliminaries and provide a unified way to show that schemes(IIV)are capable to preserve structures in Definitions 1.1-1.4 unconditionally.
Whenk=1,the recursion relationship(2.15)immediately yields the following Lemma.
Lemma 2.1For anyz/=0,it holds thatφ0(z)-zφ1(z)=1.
Lemma 2.2For anyκ >0 andτ >0,it holds that
1.φk(-τκ)>0,k ≥1;
2.φ1(-τκ)->0,∀c1≥1.
ProofUsing the definitions ofφk(z),we obtain

This completes the proof.
Theorem 2.1For system(2.13)with,assumef(t,u)meets conditions(1.2)-(1.5).Then,the ETDRK schemes(I-IV)unconditionally preserve structures in Definitions 1.1-1.4 for anyτ >0,respectively.
ProofWe prove this by induction.Consider the preservation of strong stability in Definition 1.1.By applying Lemma 2.2 to Butcher tableaux in(2.16),we can derive

Assuming‖un,j‖≤‖un‖,j=0,1,···,i-1,by using equalities(2.18),(2.19),the circle condition(1.7),and Lemma 2.1,we obtain
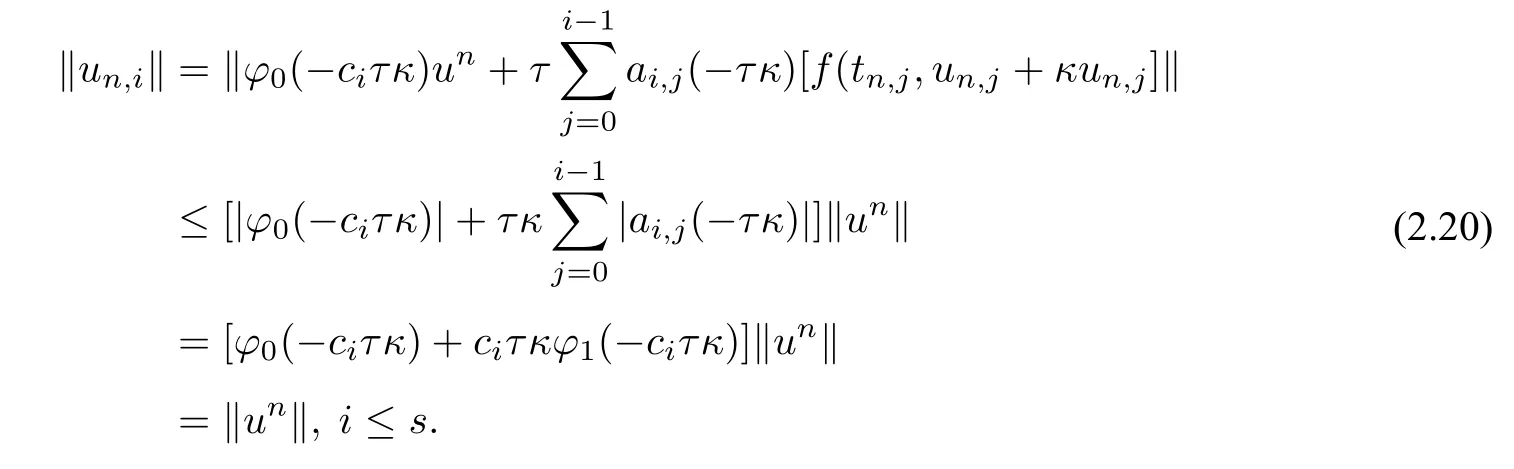
Thus‖un+1‖=‖un,s‖ ≤‖un‖.The proofs for the preservation of other structures in Definitions 1.2-1.4 can be performed similarly.

Although the ETDRK scheme of order greater than two that fulfills the conditionsai,j(-τκ)≥0,∀τκ >0,i=1,···,s;j=0,···,i-1 has not been found in the literature,given that the reformulation(2.21)can be treated as a parametric Runge-Kutta(pRK)scheme with new coefficients(-τκ)and old abscissasci,we propose to construct new high-order parametric schemes that can unconditionally preserve structures by utilizing the integrating factor approach.
2.1.2 Up to third-order single-step approach using Taylor polynomial approximation
Assume the initial conditionu0=u*is a steady state to(2.13),i.e.,f(t,u*)=0.It is expected that a numerical method will not move a solution away from the steady state.
Consider ans-stage,pth-order explicit RK scheme defined by the Butcher tableau,

whereai,j=0 (i ≤j),ci=(i=0,1,···,s),cs=1,and the Butcher coefficients are constrained by certain accuracy and stability requirements.
To develop higher-than-second-order unconditionally structure-preserving methods,two new steps are needed following Step 1 in Section 2.1.1.
Step 2Consider the Lawson transformation[61]to the unknownu(t),letv(t)=eκtu(t),we obtain an equivalent system of the stabilized formulation(2.13)

Applying a RK method to problem(2.23)and using the inverse transformationu(t)=e-κtv(t)yield the IFRK method:

Assumingun,j=u*,j=0,···,i-1,we get


We denote(2.27)[equivalent to(2.26)]as the first parametric RK method(pRK1).To preserve fixed points and strong stability,we enforce some restrictions on the RK Butcher tableau.
Assumption 2.1The underlying RK Butcher tableau satisfies
2.non-negative coefficients:ai,j ≥0,i=1···,s;j=0,···,i-1.
Lemma 2.3Assumeu*satisfiesf(t,u*)=0,and the underlying Butcher tableau satisfies the first condition in Assumption 2.1.Then pRK1 schemes(2.27)preserve the fixed points of(1.1)in the sense that ifun=u*,the solution of pRK1 satisfiesun+1=u*.
ProofBy applying the mathematical induction to(2.27),the proof can be directly carried out using the conditions≡1,i=1,···,s.
Ref.[52]shows that the conditions≡1,i=1,···,sare fulfilled by all explicit RK(s,s)(s ≤2)schemes; RK(3,3) schemes are required to satisfya2,1a1,0=,and Heun’s third-order scheme meets this condition.No higher than third-order RK(s,s)scheme meets requirements in Assumption 2.1.The derivation process is represented in Appendix A.We list some Butcher tableaux satisfying Assumption 2.1 which will be used in the numerical experiments as below.

Forward Euler scheme Ralston’s second-order scheme[62] Heun’s third-order scheme[63]
The order conditions and linear stability analysis for pRK1 were considered in[52].For completeness of this work,we present and verify those order conditions in Appendix B.It shows that if the underlying RK coefficients meet the first condition in Assumption 2.1,then the pRK1 schemes retain original convergence orders,and we have the following results.
Corollary 2.1Assumeu ∈Cp+1([0,T],RN)is the exact solution to(1.1),andun=u(tn).Then the pRK1 method with an underlyings-stage,pth-order(p=s,s ≤3)RK Butcher tableau satisfying the first condition in Assumption 2.1,has truncation errorO(τp+1),i.e.,
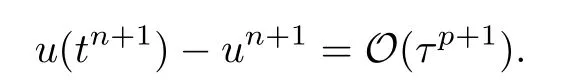
Theorem 2.2For system(2.13)withκ ≥,assumef(t,u)meets conditions(1.2)-(1.5),and the underlying RK Butcher tableau satisfies Assumption 2.1.Then,the solution obtained from pRK1(2.27)with coefficients(2.28)and abscissasci,unconditionally preserves structures in Definitions 1.1-1.4 for anyτ >0,respectively.
ProofConsider the proof of strong-stability-preservation in Definition 1.1 using mathematical induction.Assuming‖un,j‖ ≤‖un‖,j=0,···,i-1.Taking‖·‖on both sides of the equivalent formulation(2.26),and applying conditions in Assumption 2.1 and the circle condition(1.7)give

Applying the first condition in Assumption 2.1 yields

Then we obtain‖un+1‖ ≤‖un‖.The proofs for the preservation of other structures in Definitions 1.1-1.4 can be performed similarly.
Remark 2.1When considering the RK(1,1)Butcher tableau in(2.29)as the underlying scheme,the obtained first-order pRK1 scheme

is indeed a reformulation of the implicit-explicit(IMEX)Euler scheme(1.8).
2.1.3 Improved up to fourth-order single-step approaches
To derive fourth-order schemes that can unconditionally preserve structures in Definitions 1.1 -1.4,we modify Step 3 and first consider a recursive approximation [54] of eciτκusingψi(τκ) :=1 +i=1,···,s,withψ0(τκ)=1.Then the stage solutions of (2.24) are approximated by


We denote the formulation (2.32) [equivalent to (2.31)] with new coefficients(2.33) and old abscissascias the second type parametric RK method(pRK2).
In[34],Du et al.proposed to approximate the exponential functions appeared in the Shu-Osher-type IFRK formulation using combinations of exponential and linear functions.We borrow this idea and denoteBy approximating eciτκusingψi(τκ)in Step 3,we obtain the third type parametric RK method(pRK3):

Using definitions ofψi(τκ),it can be verified that both pRK2(2.32)and pRK3(2.35)preserve fixed points of(1.1).
Lemma 2.4Assumeu*satisfiesf(t,u*)=0.Then pRK2/3 schemes preserve fixed points of(1.1)in the sense that ifun=u*,the solution of pRK2/3 satisfiesun+1=u*.
We present and verify order conditions for pRK2/3 in Appendix B.Then we have the result on truncation errors.
Corollary 2.2Assumeu ∈Cp+1([0,T],RN)is the exact solution to(1.1),andun=u(tn).Then pRK2/3 schemes with an underlyings-stage,pth-order(p ≤4)RK Butcher tableau have truncation errorO(τp+1),i.e.,

Compared with restrictions on the underlying Butcher tableau of pRK1 in Assumption 2.1,the requirements on pRK2/3 are less restrictive.We show that when the underlying RK coefficients are non-negative,pRK2/3 unconditionally preserve structures in Definitions 1.1-1.4.
Theorem 2.3For system(2.13)withκ ≥,assumef(t,u)meets conditions(1.2)-(1.5),and the underlying RK Butcher tableau satisfies the second condition in Assumption 2.1.Then,pRK2(2.32)and pRK3(2.35)unconditionally preserve structures in Definitions 1.1-1.4 for anyτ >0.
ProofThe proof can be similarly carried out as Theorem 2.2 by using the second condition in Assumption 2.1,and the definitions ofψi(τκ)in pRK2 and pRK3,respectively.
Note that the classical RK(4,4)scheme with Butcher tableau
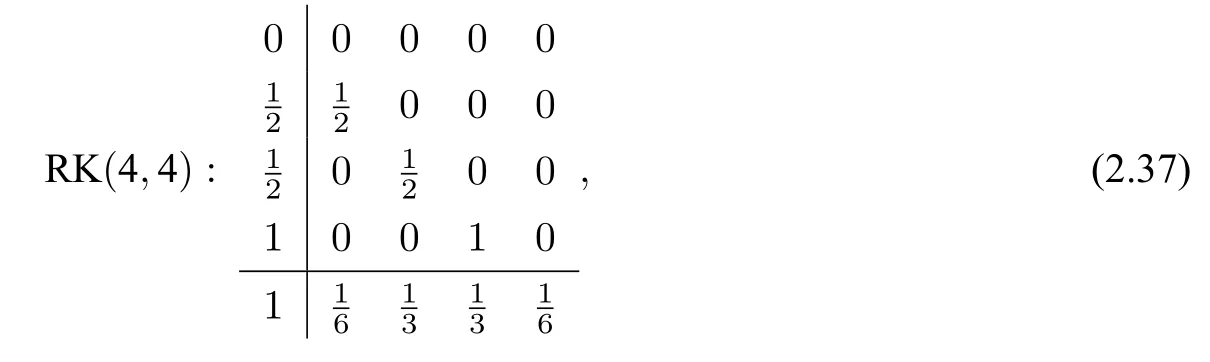
is the unique one of fourth-order accuracy with four stages satisfying the second condition in Assumption 2.1(p.521 in[14]).In addition,no explicit method of order greater than four meets the requirements of non-negative coefficients(Corollary 8.7 in[14],Theorem 4.4 in[64]).Therefore,the pRK2/3 approaches can only give at most fourth-order accurate unconditionally structure-preserving integrators.An extensive but incomplete list of non-negative RK Butcher tableaux is provided in Appendix C.
2.2 Parametric multi-step schemes
The above studies on single-step methods show that one barrier to developing high-order unconditionally SSP schemes is the non-negative restriction on coefficients.Lenferink[24]and Sand[65]proved that there is no order barrier in the explicit SSP multi-step schemes with non-negative coefficients.To derive high-order schemes,we consider the multi-step approach.We keep Step 1 unchanged and update Step 2 and Step 3 as below.
Step 2An integrating factor multi-step(IFMS)method applied to stabilized formulation(2.13)takes the form:
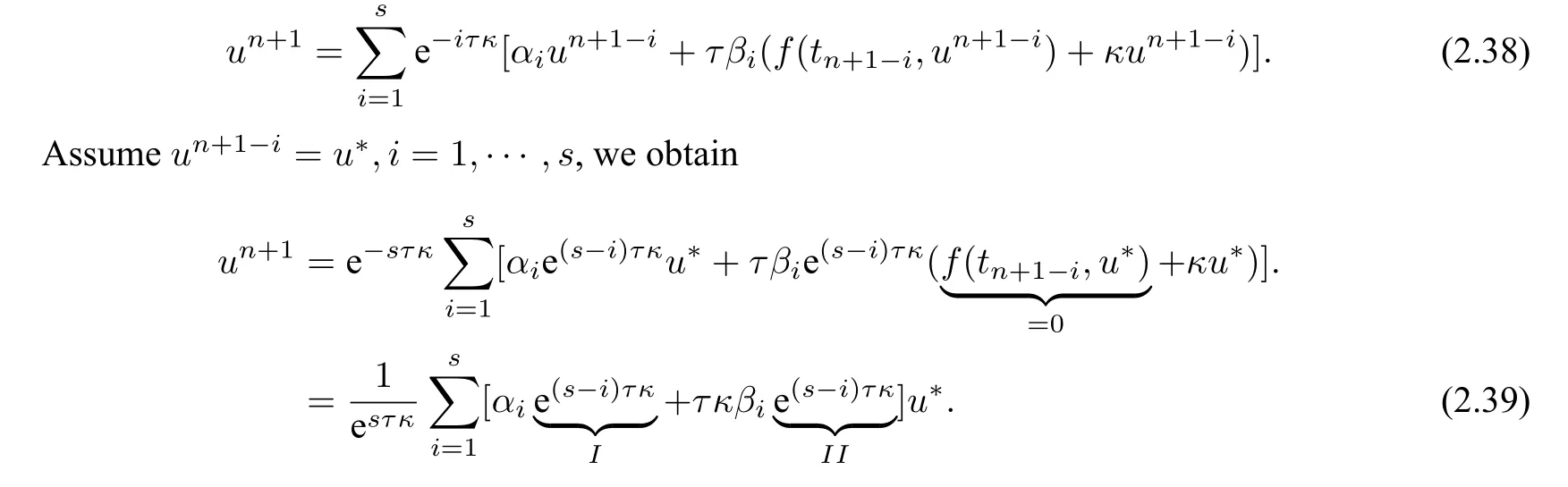
Step 3To preserve fixed-point,there are different ways [53] to approximate the exponential functions appeared in(2.39).Consider the following approximations using Taylor polynomials:
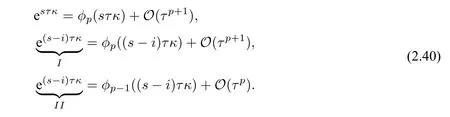
We then denote the first approximation to formulation(2.38)as parametric MS method(pMS1):

For the second approximation to the exponential function esτκ,we consider

then we get a new parametric MS method(pMS2):
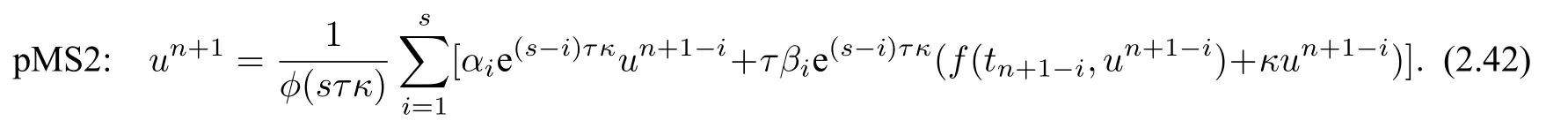
The pMS1/2 methods can be written in a unified framework:


This completes the proof.
Theorem 2.4For system(2.13)with,assumef(t,u)meets conditions(1.2)-(1.5),and coefficients of the underlying MS scheme are non-negative.Then pMS1 scheme(2.41)and pMS2 scheme(2.42)unconditionally preserve structures in Definitions 1.1-1.4 for anyτ >0.

The proofs for other structures and pMS2 can be performed similarly.
Noting that the multi-step schemes with non-negative coefficients require many steps to reach a given order,we only present some up to sixth-order underlying multi-step schemes with non-negative coefficients below.

Table 1 Multi-step methods with non-negative coefficients[6]
3 Parametric methods for stiff nonlinear systems
In this section,we consider stiff,nonlinear ODE systems in the form

with a stiff constant coefficient linear termLu,L ∈RN×Nthat satisfies the forward Euler condition

which is equivalent to the circle condition

and the nonlinear termf(u)satisfies the circle condition(1.7).We assume that the allowable time-step for the forward Euler condition on the linear component is significantly smaller than the one for the nonlinear component,i.e.,The SSP integrating factor approaches for (3.48) have been previously studied by Isherwood et al.[67,68,69].Their studies showed that the integrating factor approach only requiresτ ≤CτF E,which greatly relaxed the requirementson explicit SSP schemes;andτ ≤minon IEMX SSP RK schemes[70],whereCand ¯Care SSP coefficients of the explicit and implicit parts,respectively.
Isherwood et al.[67]proved that when the linear term satisfies the forward Euler condition(3.49),the following Lemma holds.
Lemma 3.1([67]) AssumeLusatisfies(3.49)for some value ofThen
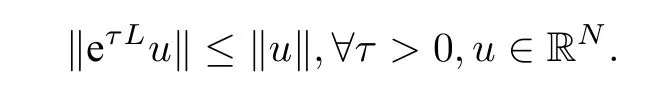
By introducing the termκ(u-u)to(3.48),we obtain
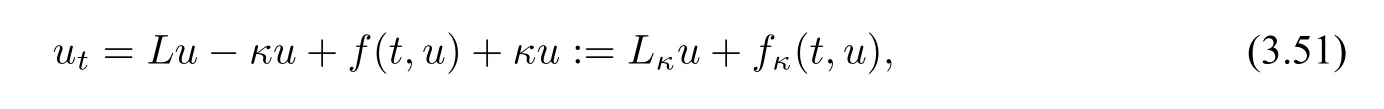
whereLκ=L-κI,I ∈RN×N,fκ(t,u)=f(t,u)+κu.Then taking the stiff matrixLκas the variable ofφjfunctions in(2.16),we obtain the stabilized ETDRK schemes
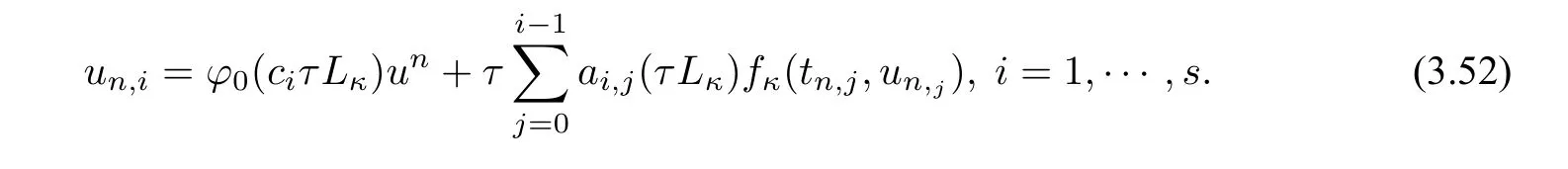
Lemma 3.2For anyκ >0 andτ >0,it holds that

This completes the proof.
Before showing properties of the stabilized first-and second-order ETDRK schemes with Butcher tableaux(2.16),we present the following lemma.
Lemma 3.3Assume the linear termLu,u ∈RNsatisfies following conditions:


where the inequalities are element-wise.
ProofConsider the result on positivity as an example.We carry out the proof by adopting the approach used in Theorem 1 of[67].
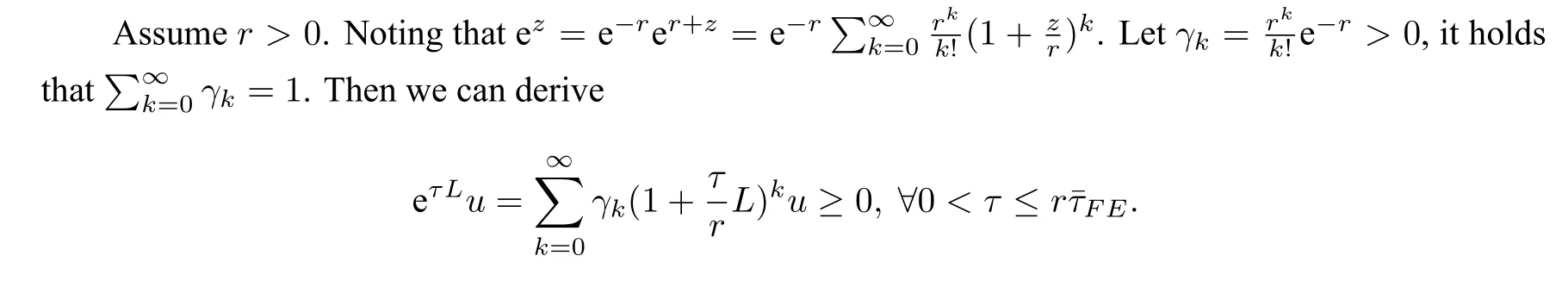
Sincercan be arbitrarily large,we have eτLu ≥0,∀τ >0,u ≥0.
The other results can be proved in the same way.
Theorem 3.1For system (3.48) with,assumeLusatisfies one or more conditions in(3.49),(3.53)-(3.55),andf(t,u)satisfies the corresponding conditions(1.2)-(1.5).Then,the ETDRK schemes(I-IV)unconditionally preserve structures in Definitions 1.1-1.4 for anyτ >0,respectively.
ProofWe prove this by induction.Consider the preservation of strong stability in Definition 1.1.
Assuming‖un,j‖ ≤‖un‖,j=0,1,···,i-1.By using Lemmas 3.2,2.1,and equalities (2.18),(2.19)we obtain
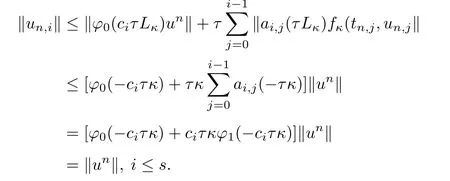
Thus‖un+1‖=‖un,s‖ ≤‖un‖.The proofs for preservation of other structures in Definitions 1.2-1.4 can be performed similarly.
For other parametric methods proposed in Sections 2.1 and 2.2,let us consider the pRK1,pRK2 and pMS1 schemes.By applying the integrating factor method (with integrating factor e-tL) with the underlying parametric schemes,we obtain
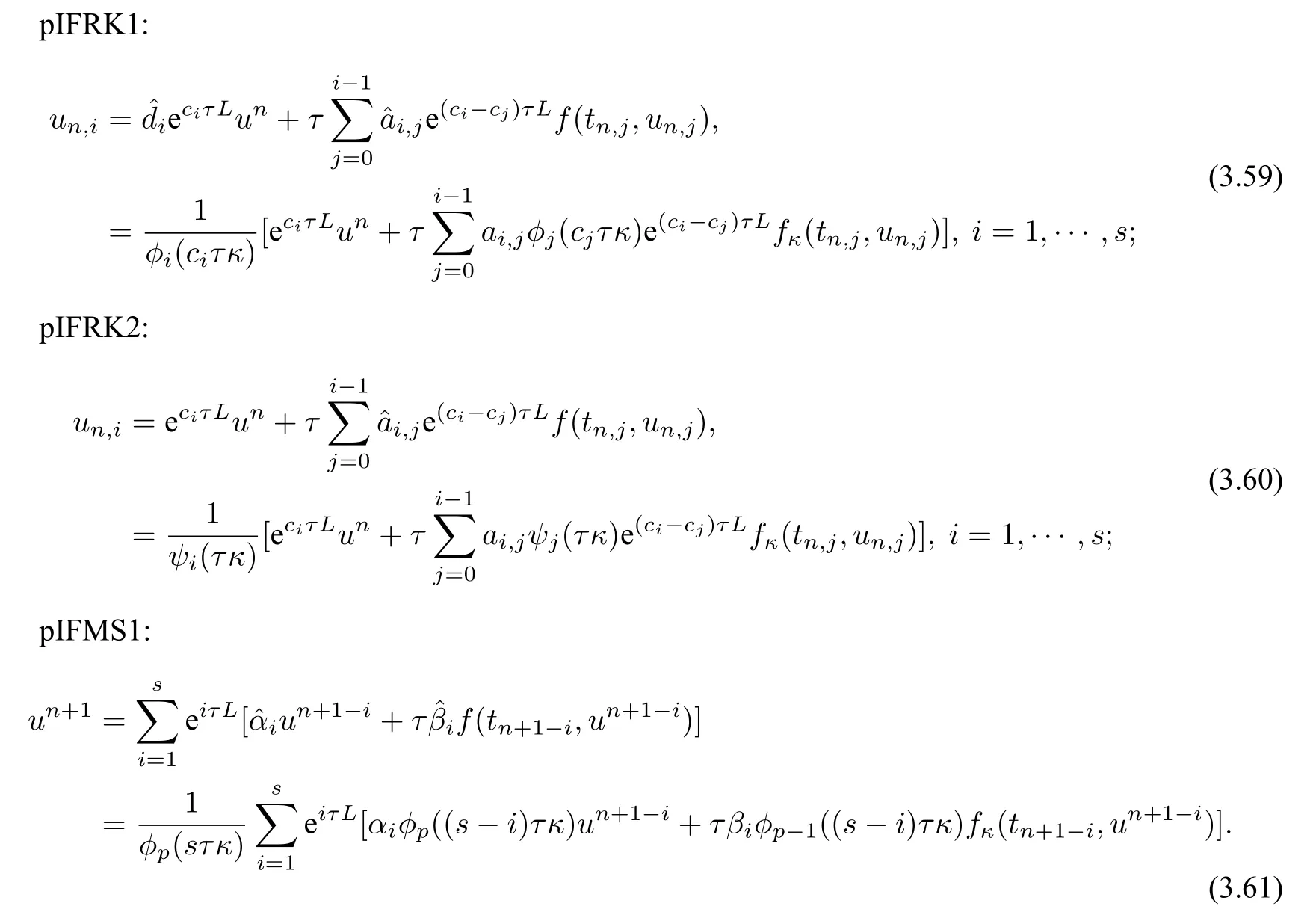
Then we have unconditional preservation of structures in Definitions 1.1-1.4.
Theorem 3.2For system(3.48)with,assumeLusatisfies one ore more conditions(3.49),(3.53)-(3.55),andf(t,u)satisfies corresponding conditions in(1.2)-(1.5),respectively.If
1.pIFRK1:the underlying RK Butcher tableau satisfies Assumption 2.1,and non-decreasing abscissas:0=c0≤c1≤c2≤···≤cs=1;
2.pIFRK2/3:the underlying RK Butcher tableau satisfies the second condition in Assumption 2.1,and non-decreasing abscissas:0=c0≤c1≤c2≤···≤cs=1;
3.pIFMS1/2:coefficients of underlying MS scheme are non-negative;then the proposed pIFRK1/2/3 and pIFMS1/2 schemes unconditionally preserve structures in Definitions 1.1-1.4,respectively.
ProofBy applying Lemmas 3.1,3.3 and assumptions in Definitions 1.1-1.4,the proofs can be done similarly as Theorem 3.1.
Remark 3.1When both linear and nonlinear terms satisfy the circle conditions,we point out that by treating bothLuandf(t,u) explicitly,the stabilized ETDRK (depending onφk(-τκ)),pRK1/2/3,and pMS1/2 can unconditionally preserve those structures when.However,a larger stabilization parameter will lead to more truncation errors.Thus,the strategies proposed in this section is preferable than those presented in Section 2 when considering stiff systems in the form(3.48).
4 Numerical experiments
In this section,we underline our theoretical analysis with numerical experiments.For the convenience of discussion,we consider the preservation of strong stability as an example.Because of limitation of space,an extensive investigation on other applications with respect to positivity,range boundedness and contractivity will be carried out in a future work.When adopting the ETDRK and parametric integrating factor schemes,we compute products of matrix exponentials with vectors via the fast Fourier transform to accelerate the computations[37].We adopt the Butcher tableaux in(2.29)as the underlying RK schemes for pRK1/2/3.
4.1 Convergence study
Example 4.1To demonstrate the convergence orders of the proposed schemes,we consider a linear advection equation with periodic boundary conditions:

We seta=1,and employ a standard first-order upwind finite difference method for the advection term.LetNdenote the number of grid points,and the mesh size beh=.Denote the grid points as Ωh={xj|xj=jh,j=0,1,···,N -1}.Let VN={v|v=(vj),xj ∈Ωh} ⊂RNbe the space of grid functions defined on Ωh.The first-order differentiation matrix is denoted asD.Then we solve the resulting linear systemut=f(t,u):=-aDuusing the time integration schemes proposed in Section 2.The numerical errors are computed using
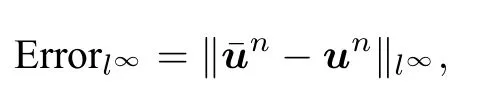
Resultsof a numerical convergence study atT=2-4obtained by ETDRK,pRK1/2/3 and pMS1/2 for the linear advection equation (4.62) are shown in Fig.1.Each of the proposed schemes converges with the expected order of accuracy.Noting that ETDIV(c1=2)scheme satisfies part of the third-order conditions[58],thus it is much more accurate than those second-order schemes in Fig.1(a).By comparing results in Fig.1(c)and(d),it shows that the numerical errors of pRK3(resp.pMS2)schemes are smaller than those of pRK2(resp.pMS1),because of the approximations using a combination of exponential and linear functions.Note that the first-order pRK1/2/3 schemes are indeed the same,thus the error curves of pRK2/3 in Fig.2(c)overlapped.

Figure 1 Time accuracy tests of ETDRK,pRK1/2/3,and pMS1/2 schemes.Reference slopes in(a),(b)and(c)are fixed.Colored dashed curves in(c)and(d)denote errors obtained using pRK3 and pMS2 schemes,respectively
4.2 Strong-stability-preserving tests
Example 4.2The strong-stability-preservation of the proposed schemes will be tested on a linear advection equation with discontinuous initial data and periodic boundary conditions:

We denote the semi-discrete system obtained by upwind scheme asut=Lu+N(u),whereL=-aDandf(t,u)=-Du.Since Fig.1 demonstrates that pRK3 and pMS2 are more accurate than pRK2 and pMS1,respectively.For comparison and simplicity,we test the strong-stability-preservation using the high-order pIFRK3 and pIFMS2 schemes.When the stabilization parameterκ=0,the resulting pIFRK3 and pIFMS2 schemes become the traditional IFRK and IFMS schemes.We setN=1000,τF E==1000,and solve this problem for 100 time steps.The results of maximum rise in TV obtained by second-to fourth-order RK-type schemes,and fourth-to sixth-order MS-type schemes witha=0,5,10 are presented in Fig.2.It can be observed that the allowable time steps of IFRK and IFMS schemes become larger with increasinga.This phenomenon agrees well with the conclusion of[67]that significant damping occurs due to the exponential terms,thus reduce the oscillation and its associated rise in total variation.The results computed by parametric schemes are noteworthy.Because of the introduction of stabilization parameter,we can clearly observe that all pIFRK3 and pIFMS2 schemes preserve the strong stability without restriction onτ.
In Fig.3,we present the solution profiles computed by different schemes witha=0 att=0.15.We choose a critical time-step sizeτ=0.00102 for IFRK and pIFRK3 schemes.Fig.3(a)demonstrates that the standard IFRK(2,2) generates oscillations for this time step,while the pIFRK3(2,2) scheme eliminates the spurious oscillations,but time delay appears because of introduced truncation errors.With the increasing of temporal order,the solution delay becomes weaker,and the fourth-order pIFRK3(4,4)gives very accurate solution.The time step for IFMS(5,4)and pIFMS2 are chosen asτ=0.0000277>CτF Eandτ=0.000277,respectively.Again,the pIFMS2 scheme not only gives very accurate solutions,but also accelerates the computation by allowing a ten times larger time-step size.
5 Concluding remarks
This is the first work to develop high-order accurate and explicit methods that can unconditionally preserve strong stability,positivity,range boundedness and contractivity,by trading off accuracy for stability.
By taking the circle condition into account when adopting the stabilization technique,a series of high-order accurate and unconditionally structure-preserving schemes are constructed using newly developed approximation techniques,i.e.,(1) a Taylor polynomial approximation adopted in pRK1 and pMS1; (2) a recursive approximation adopted in pRK2; (3) a combination of exponential and linear functions adopted in pRK3 and pMS2.
Theoretical analysis and numerical tests demonstrated the accuracy,stability and strong-stabilitypreservation of proposed schemes.Noting that the conditionensures the preservation of structures for any time-step sizeτ.In practice,we can only choose a finite time-step size because of the limitation of accuracy.Consequently,a value ofκthat is no larger than,but depends onτ,τF Eand the SSP coefficientCof underlying schemes can be expected to preserve the structures.In addition,from order conditions(2.47)and those in Appendix B of parametric schemes,we observe that apth-order parametric scheme indeed re-scales the time step size fromτtoτ+O(τp+1).
Since it is not a trivial task to adaptively decide the stabilization parameter,eliminate the time-delay phenomenon or investigate other stabilization terms,e.g.,the Douglas-Dupont regularization termκΔ(uu),we leave these issues to our future work.
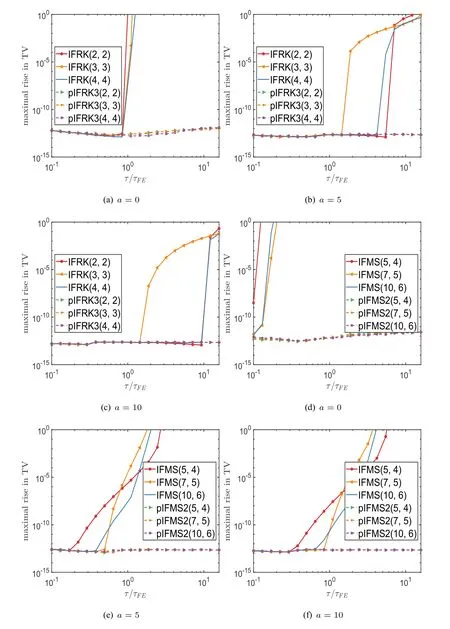
Figure 2 Example 4.2:The maximum rise in TV computed by different RK-type schemes(top row),and MS-type schemes(bottom row)for 100 time steps.Parameters: N=1000,κ=N for parametric schemes

Figure 3 Example 4.2:Solutions computed by IFRK (τ=0.00102),pIFRK3 (τ=0.00102),IFMS (τ=0.0000277),pIFMS2(τ=0.000277).Solutions of pIFMS2 overlapped.Parameters: a=0,N=1000,κ=1000
Appendix
A.Derivation of pRK1 schemes


Table A1 Order conditions for explicit RK(s,p)schemes(ci=ai,j)

Table A1 Order conditions for explicit RK(s,p)schemes(ci=ai,j)
By using the order conditions for underlying RK schemes presented in Table A1,we conclude the following:
3.RK(3,3)satisfies1,i=1,3.The equality1 holds whena2,1a1,0=.In the literature,we find that Heun’s method[RK(3,3)in(2.29)]meets this condition;
B.Order conditions for pRK1/2/3 schemes
The Butcher tableaux of pRK1/2/3 schemes can be written in a unified form

By performing tedious expansions,we verified that first-to third-order pRK1 schemes with RK Butcher tableaux satisfying the first condition in Assumption 2.1,meet the order conditions in Table B1.For better illustration and to save space,we verify order conditions for pRK1(3,3)as below.
Verification of pRK1(3,3):

For the up to fourth-order pRK2 and pRK3 schemes,we consider the third-order pRK2 scheme as an example.The verifications of fourth-order conditions of pRK2/3 schemes were carried out using Matlab in[54].
Verification of pRK2(3,3):

C.An incomplete list of RK Butcher tableaux that have non-negative coefficients and non-decreasing abscissas


