热/声耦合方程的解耦分析和数值求解

朱丽艳 邓又军 段超华 李滔

(中南大学数学与统计学院,分析数学及其应用湖南省重点实验室,长沙,410083)

1 引言

热弹性力学作为固体力学的一个分支,具有重要的工程实际意义,其耦合理论受到了国内外学者的关注和研究[1,2].本文研究均匀各向同性介质中的相互耦合的热弹性波动方程和热传导方程的解耦分析和有限差分法的数值实现.相对于其他方程而言,双曲型方程的数值求解存在诸多困难,如出现数值振荡现象,难以得到稳定的差分方法[3].孙卫涛在[4]中给出了二维均值同性介质弹性波动方程的差分格式,得到了显示差分格式,并分析了稳定性条件.对于热声耦合下的热弹性波动方程,并未有学者进行差分研究.目前波动方程的数值方法主要有伪谱法[5],有限元法[6],边界元法[7],谱元法[8],有限差分法等.有限元法和有限差分方法相比,有限元法耗时长,而有限差分法具有简单灵活、计算效率高以及占用内存小等优势,广泛应用于地震波场数值模拟[9].随着科研及工程应用中对数值模拟精度的要求不断提高,近年来,传统有限差分法在数值频散、稳定性方面的不足逐渐显现.紧致差分格式是一种精度和分辨率高的格式,并且具有很好的稳定性[10].

本文参考周诚尧等[9,11,12]对地震波方程的五点CDD8 差分格式,以及[3]中数值黏性修正理论,推导得到数值黏性项,并使用迭代的方法求取四阶导和带混合项的高阶导,对CDD8 格式进行推广,对热声耦合的热弹性波动方程进行差分实现.

2 耦合原理

在高温固体介质内部,声波的传播受到热声固多物理场控制,由热弹性力学理论,控制方程由相互耦合的热传导方程和热弹性动力学方程组成.

2.1 热弹性波动方程

张量形式的热弹性动力学方程由质点动力学方程、几何方程以及热弹性本构方程耦合而成:

其中ui为质点位移;σij,ϵij分别为应力和应变张量;ρ为材料密度;fi为外界施加的激振力;Dijkl为材料的弹性模量张量;βij为热力耦合张量,表示增加单位温度时压应力的增量;T为温度.

将本构方程、几何方程代入质点动力学方程,得到各向异性介质中的波动方程:

对于均质的各向同性介质,热力耦合张量βij以常数β表示,当不存在外力作用时,得到均质各向同性介质中的热弹性波动方程:

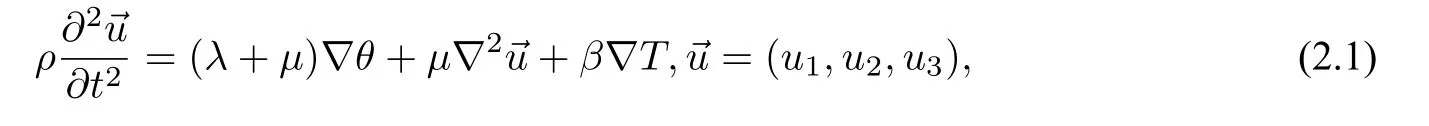
其中,

是拉普拉斯算子;

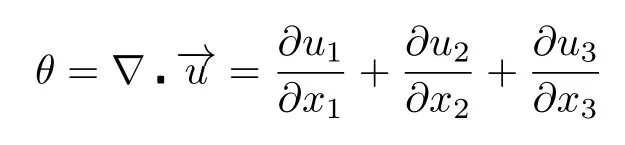
是体积应变;

是体积应变的梯度;β∇T为耦合项,表示在非均匀温度场影响下,由热膨胀产生的体积力源项.

2.2 热传导方程

根据热固耦合原理,结构变形会对热量传递过程产生影响,热传导方程可表示为

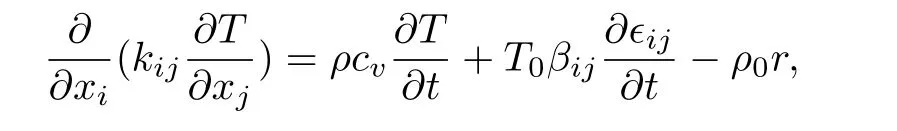
式中,cv为材料定容比热容,r为热源,kij为导热系数张量.

对于均质各向同性介质,导热系数张量kij以常数k表示.将几何方程代入,若不考虑热源的影响,修正的热传导方程可简化为:

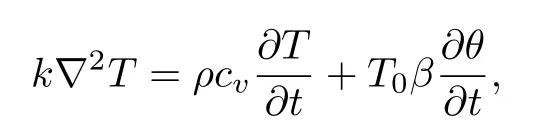
方程(2.1)和(2.2)构成了固体结构内部的波传播和热传导耦合的控制方程,即热弹性波动方程、热传导方程,二者通过介质声学参数的温度效应、弹性变形等耦合在一起,大大增加了问题求解的难度.

3 解耦分析

考虑热弹性波动方程和热传导方程在求解过程中时间推进上的不同.当介质的长度为l时,在热传导方程中,表征内部温度场对边界热扰动响应的特征时间tc为:

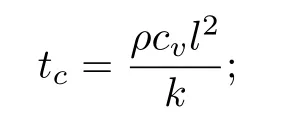
在波动方程中,表征内部应变位移场对边界扰动响应的特征时间te为:

比较tc与te,二者存在巨大的量级差异,tc远远大于te,即温度场受到结构变形所产生的影响可以忽略不计,因此,固体结构中波动方程与热传导方程的双向耦合,可以解耦为顺序耦合.

解耦的计算分析流程可以描述为:首先求解热传导方程获得模型内部瞬态温度场,进行结构热分析;然后将温度场作为附加的热载荷,在声扰动的激励下求解波动方程,得到结构的应变位移场,应变位移场对温度场的影响忽略不计.计算流程见图1.

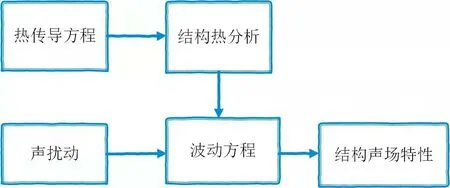
图1 固体结构中热/声耦合分析计算流程

4 有限差分数值求解

热弹性波动方程存在时间项和空间项的二阶导数,差分格式涉及到至少前后三层的时间和空间位移.本文将从时间维度推进计算,在有限差分法的基础上,引进数值黏性修正手段和五点CDD8 格式提高差分方法的稳定性和精度.利用时间Taylor 方法[3]推导得到数值黏性（修正）项,从而提高差分格式的稳定性.由时间Taylor 方法得到的数值黏性项为时间方向的四阶导数,利用方程的等式关系,将时间四阶导转化为空间导数.由于空间四阶导的中心差商需要用到前后各两个点,使得边界处理更加困难,因此,本文参考[11,12],引入五点CDD8 格式.二维均质各向同性介质,张量形式的热弹性动力学方程,在不存在外力作用时,可以表示如下:

(4.1)可拆分为以下两个方程

其中=(u1,u2)u1=u1(t,x1,x2),u2=u2(t,x1,x2),T=T(t,x1,x2).为了表示方便,记=(u,v)u=u(t,x,y),v=v(t,x,y),T=T(t,x,y).上述方程进一步化为:

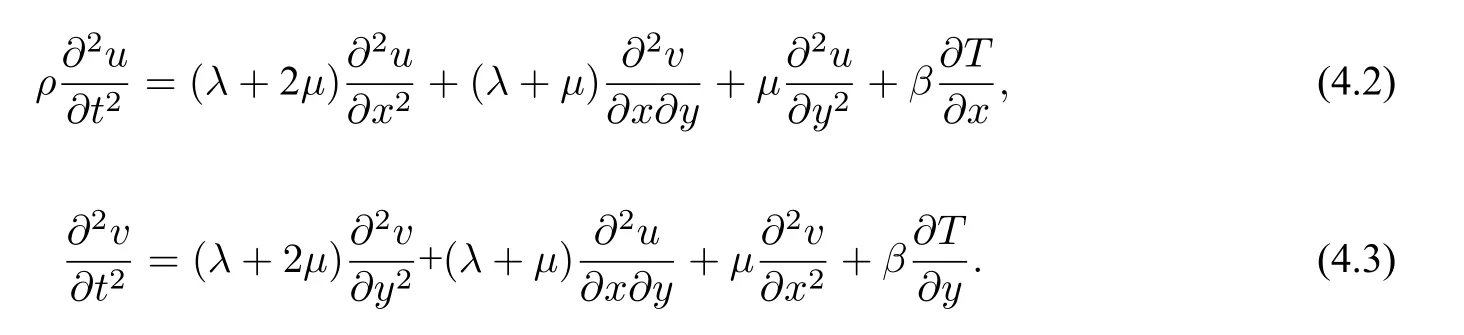
4.1 网格划分和时间离散

选定矩形区域[a,b]×[c,d]作为差分区域,对其进行网格划分:取空间步长h,时间步长τ,网格划分为:

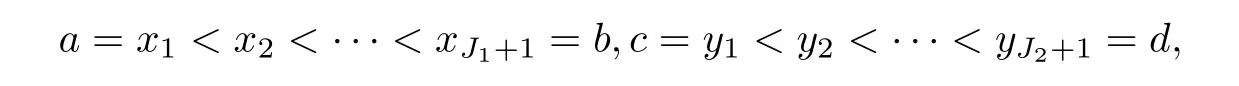
其中,J1=(b-a)/h,J2=(d-c)/h,xi=a+(i-1)h,i=1,2,···,J1+1,yj=c+(j-1)h,j=1,2,···,J2,J2+1.

差分得到的数值解记作:

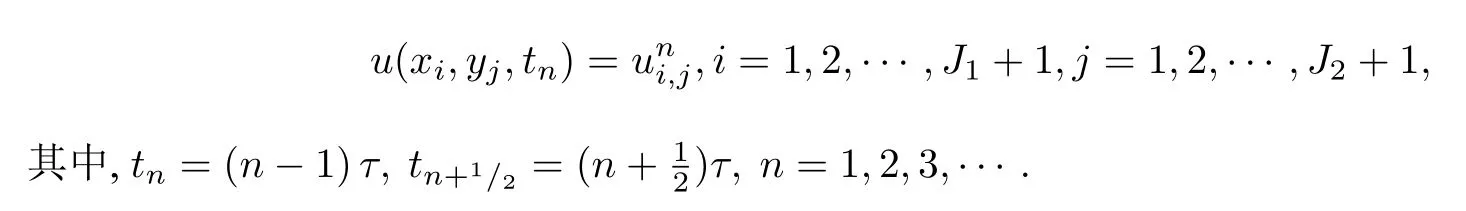
4.2 初边值条件的处理

4.2.1 初值条件的处理

根据初始条件u(0,x1,x2)=φ1(x1,x2),v(0,x1,x2)=φ2(x1,x2),得到第一层(n=1)的函数值:

(4.5)可化为:

由初始条件ut(0,x1,x2)=ψ1(x1,x2),vt(0,x1,x2)=ψ2(x1,x2),用中心差商代替ut,得到:

在(4.6),(4.7)中,令n=1,得

联立(4.10),(4.8),消去虚拟项,得到第二层(n=2)各网格点上的值的表达式:

同理,联立(4.11),(4.9),消去虚拟项,得到第二层(n=2)各网格点上的值的表达式:

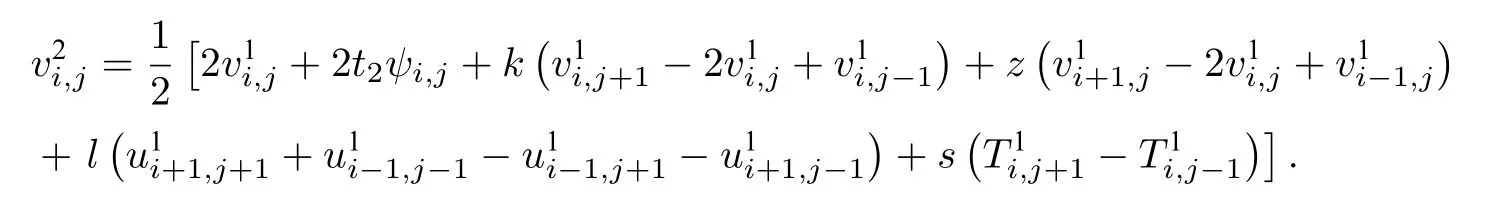
4.2.2 边界条件的处理

由边界条件:

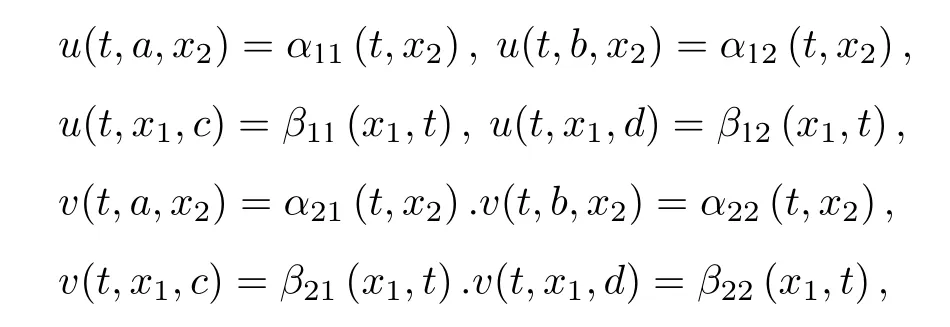
得到边界点:

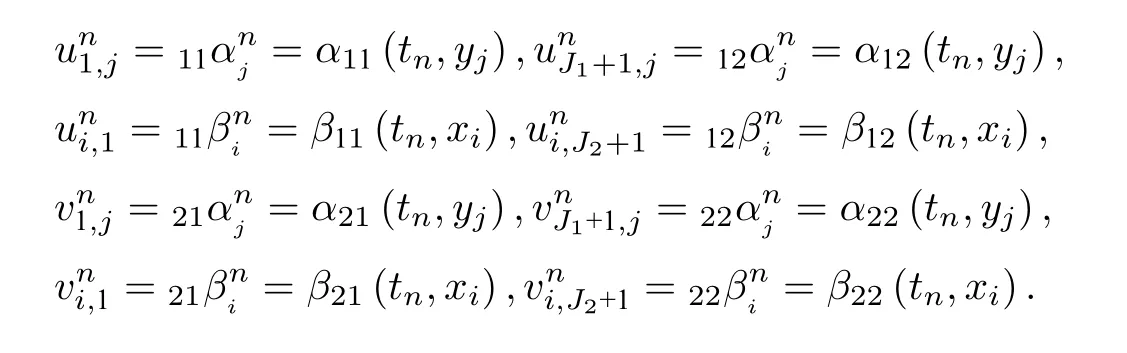
4.3 差分实现

首先解热传导方程,参考[3]中经典的向前差分法,可得到热传导方程的稳定算法,得到的解存为对方程(2.1),(2.2),利用时间Taylor 方法,有

将两式相加得

对于v,同理可得

这样相当于给了时间方向四阶的精度.利用原方程空间导数和时间导数的关系,把时间导数化为空间导数:

以上得到的空间四阶导项和温度场三阶导项为数值黏性（修正）项.

因为边界处四阶导的差分,需要用到更多的点,至少是前后四个点,边界处理变得更困难,所以用五点CDD8 格式近似代替空间二阶导数和四阶导数.超紧致有限差分格式在紧致差分格式基础上发展而来,1998 年KRISHNAN 提出了如下的五点CCD8 格式[13]:

利用上述导数和函数的关系式,可推导导数由函数表示的表达式,从而得到导数的差分.

以x方向为例,说明利用五点CCD8 格式求解公式中u对x的偏导数的过程.

假设U为位移场,A为公式左端的差分系数矩阵,B为公式右端的差分系数矩阵,F为待求位移场空间一阶和二阶导数矩阵,将上式化成矩阵形式:AF=BU.

·二阶导数的求法:

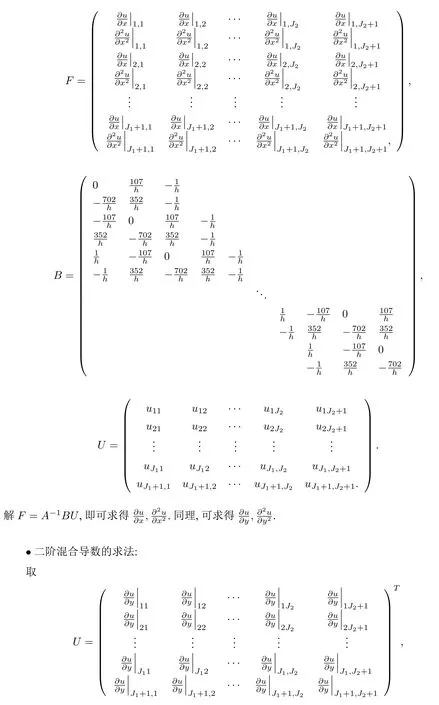
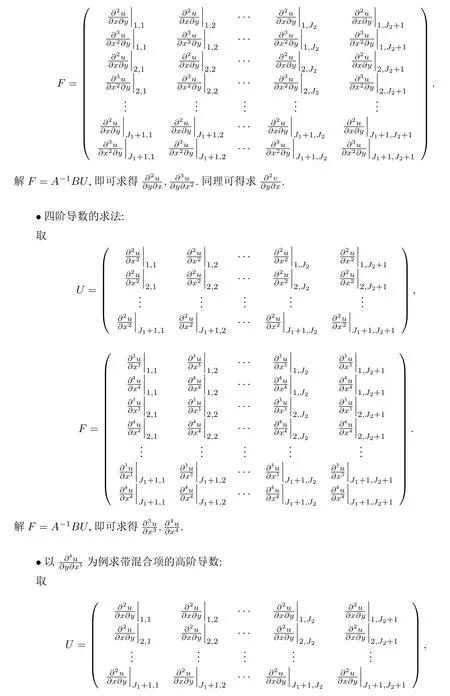
解F=A-1BU,即可求得.其余的带混合项的高阶导数也可以类似求得.

以上,我们得到了所有空间二阶导、二阶混合项导数、四阶导、带混合项的高阶导的差分格式,将其代入公式(4.14),(4.15)便可得到弹性波动方程(2.1)的差分格式.

4.4 算例

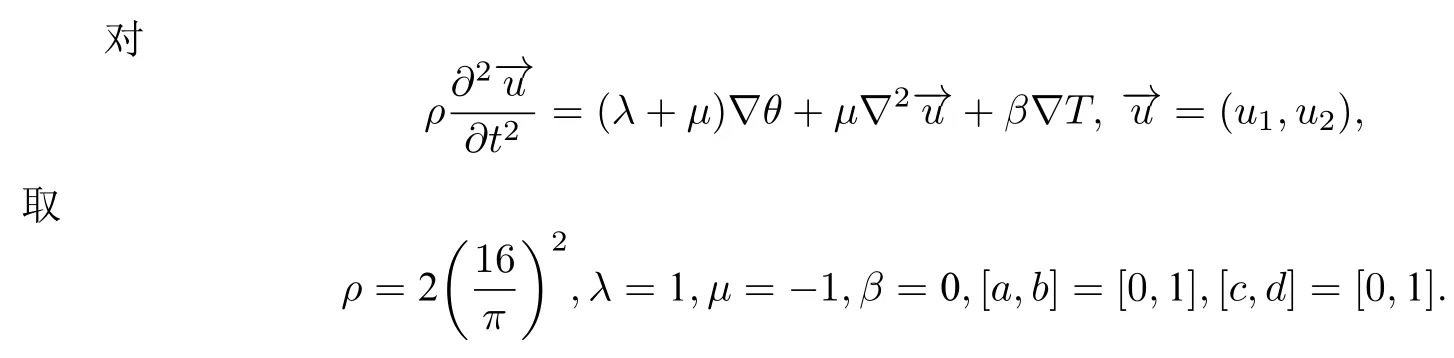
4.5 数值求解结果

本文以时间推进的方式进行计算,本节设置数值实验,观察算法精度和空间网格的关系,以及误差随时间推进是否产生传递.

粗网格下数值解和精确解的比较见图2,其中,空间步长为0.1,时间步长为0.01,运算至n=300,即t=3s 时停止.

细网格下数值解和精确解的比较见图3,其中,空间步长为0.05,时间步长为0.01,运算至n=300,即t=3s 时停止.

通过比较图2和图3,可以看出,误差随着空间网格的加密而减小.

细网格下t=5s 时数值解和精确解的比较见图4,其中,空间步长为0.05,时间步长为0.01,运算至n=500,即t=5s 时停止.

通过比较图3和图4,可以看出,误差和解的大小一起随着时间的推进而衰减,没有出现误差积累的情况,算法在此种网格下是稳定的.

5 结论

1.本文研究了均匀各向同性介质中的相互耦合的热弹性波动方程和热传导方程的解耦和有限差分法的数值实现.根据热传导方程和弹性波动方程的特征时间推进上的不同,将双向耦合解耦为顺序耦合,首先求解热传导方程,然后将温度场作为附加的热载荷,求解热弹性波动方程.

2.热传导方程采用经典的有限差分法进行求解,本文采用显示向前差分法;然后将数值粘性修正原理及五点CDD8 格式应用到弹性波动方程的有限差分中来,通过Fortran 语言进行编程实现.本文数值结果表明,精度和计算效率都较为理想.

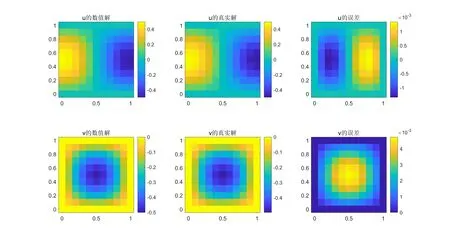
图2 t=3s 时的数值解求解结果

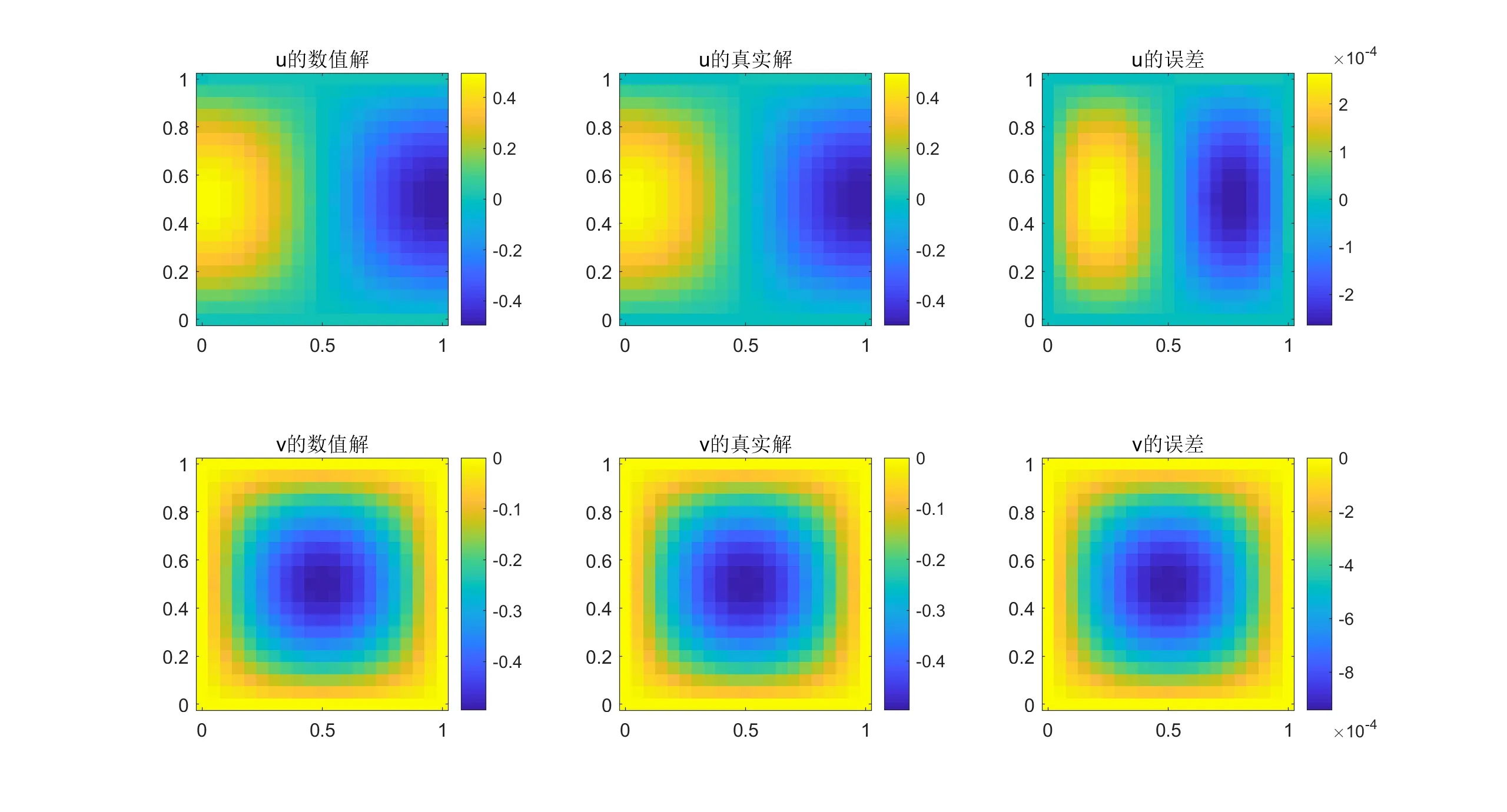
图3 网格加密后t=3s 时的数值解求解结果

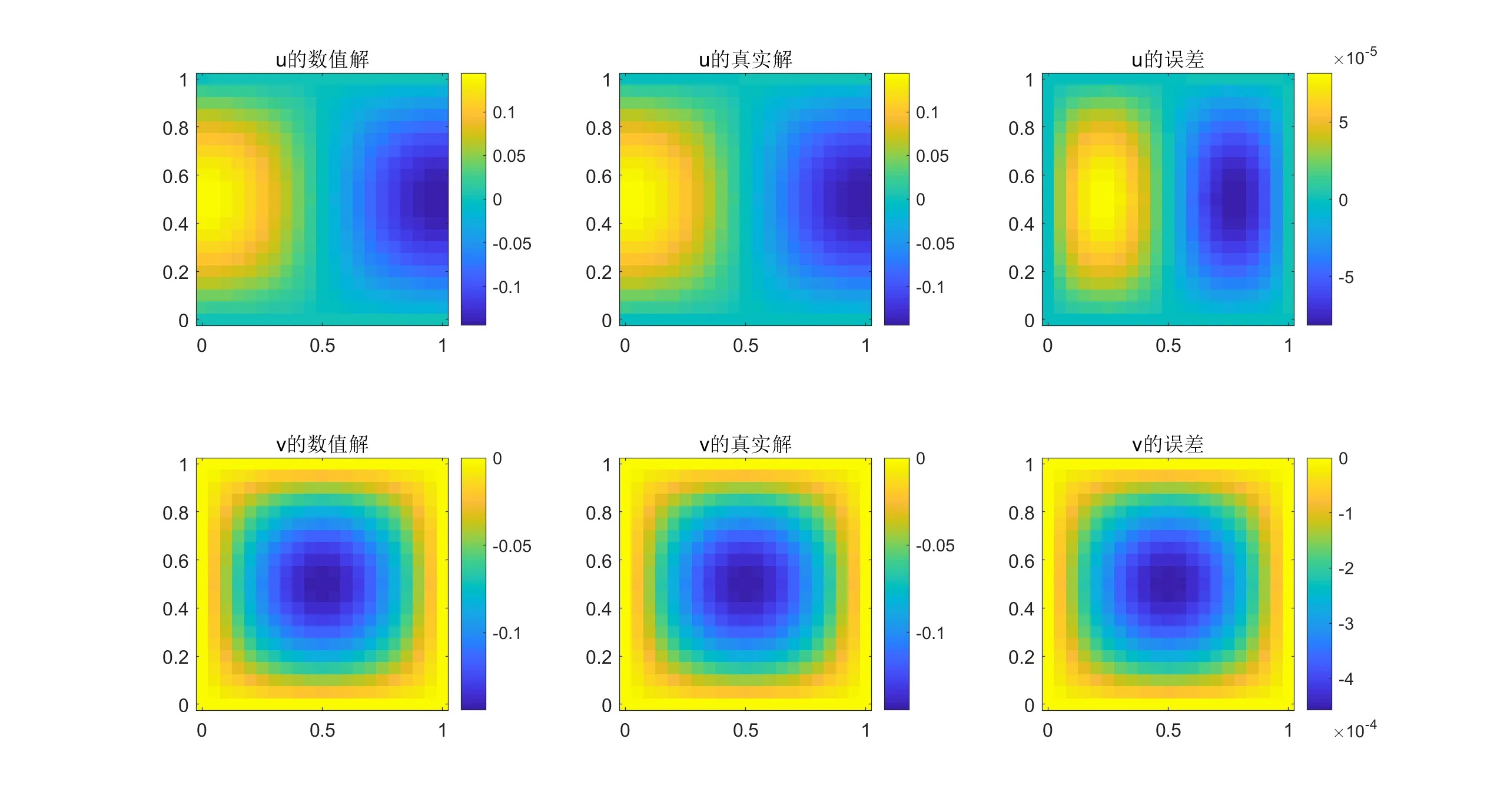
图4 网格加密后t=5s 时的数值解求解结果