求解常数噪声环境下时变非线性方程的离散时间零化神经网络*

孙 敏, 孙洪春, 葛 静

(①枣庄学院数学与统计学院,277160,枣庄市；②临沂大学数学学院,276000,山东省临沂市)

0 引 言

科学研究离不开数学,而数学模型是自然科学与社会科学领域中许多实际问题的数学描述.在各类数学模型中,方程是一类最基础,也是应用最广泛的数学模型之一,其不仅可以直接描述自然规律,而且也是其他一些数学模型的等价形式,因而方程的理论与算法研究具有基础、底层研究的意义.各类方程的研究,尤其是算法研究,吸引了众多学者的目光,相应的研究成果不可胜数.

众所周知,运动是绝对的,静止是相对的,因而动态的世界要求我们用动态变化的眼光去看问题.于是学者们提出了一类描述动态问题的时变数学模型,包括时变线性方程、时变非线性方程及时变最优化问题等[1,2].本文拟研究时变非线性方程问题的数值求解算法.作为一个特殊的递归神经网络,归零神经网络(ZNN)是求解各类时变问题的一个标准算法,该方法由张雨浓教授于2002年首次应用到求解时变问题中[3].连续时间ZNN算法是基于放射性元素衰变的微分方程,该微分方程的解以指数速度快速收敛到零.以该微分方程为控制律,将时变问题的残差代入后可得到连续时间ZNN算法.因此从理论上只要微分方程的解收敛到零,则该微分方程都可以作为控制律而得到一个连续时间ZNN算法.早期ZNN的研究主要集中在将其应用到各种时变问题的求解中.在2010年之后,借助各类一步前向差商公式,学者们又提出了各类离散时间ZNN算法.这里面比较有代表性的成果包括：基于一步差商公式,Zhang等[4]首次提出了一类离散时间ZNN算法,并将其应用到求解时变四次根的求解问题中；为了提高求解精度,基于三步差商公式,Jin和Zhang[5]提出了一类三步离散时间ZNN算法,并将其应用到机械臂路径规划中.而后,具有更高精度的离散时间ZNN算法陆续被提出,2019年Sun等[6]给出的一般六步离散时间ZNN算法.在离散时间ZNN算法中,步长是一个很重要的参数,其取值过大,则离散时间ZNN算法可能不收敛,取值过小则计算量太大.Jin和Zhang[7]首先关注了这个问题并给出了步长的有效范围,而后Sun等[6,8,9]对该问题进行了细致的研究,借助Jury稳定判据,给出了一般的一步到六步离散时间ZNN算法步长的有效区间.

在ZNN算法的研究过程中,另一个重要的突破是由Jin和Zhang[10]提出的带积分项的连续时间ZNN算法,该算法最大的优点是可以完全抑制模型的常数噪声,并且线性噪声下该算法产生的稳态误差反比于设计参数.该算法激起了ZNN算法研究的一次热潮,学者们陆续提出了许多不同类型的抗噪声ZNN算法,有一些甚至可以加速到有限时间收敛(理论上)或完全抑制线性噪声.最近的研究文献虽然也提出了一些噪声环境下的离散时间ZNN算法,但是这些算法都是将积分-微分型连续时间ZNN算法转化成一个一阶微分方程组,进而对微分方程组中的导数采用一步前向差商进行近似,这与无噪声环境下的处理方式是完全一样的.这样处理产生了3个问题：(1)所设计的离散时间ZNN算法的变量个数增加了一倍,这使得问题的规模变大了.(2)所设计的离散时间ZNN算法中含有未知噪声,而在实际问题中噪声只是客观存在的,但其具体表达式往往是无法直接观测的.(3)无法分析所设计离散时间ZNN算法中参数的取值范围,这主要是因为微分方程组中各个微分方程的系数是不一样的,并且变量是耦合的,所以我们无法将其转化一个具有同样系数的差分方程组,进而无法利用Jury稳定判据给出参数的有效范围.在数值实验部分我们将通过具体例子来说明如果这些离散时间ZNN算法参数取的不合适,则其是发散的.

本文将对这些问题给出一个系统的解决方案,提出了一类常数噪声环境下的离散时间ZNN算法.具体的,我们利用一步前向差商近似CT-ZNN的导数,利用左(右)矩形公式近似CT-ZNN的积分,得到了一个抗常数噪声的离散时间ZNN算法.进而,我们利用Jury稳定判据给出了该离散时间ZNN算法中参数取值范围的估计,同时证明了其它数值积分公式导出的离散时间ZNN算法是不稳定的.最后,我们将所提出的离散时间ZNN算法应用到了时变非线性方程问题.

1 连续时间ZNN算法

本文考虑时变非线性方程(time-varying nonlinear equation，TVNE),其具有如下数学结构：求x(t)∈Rn满足

f(x,t)=0,t∈[0,tf]

(1)

其中映射f:Rn+1→Rn关于变量x,t可导,tf>0表示所研究问题的最终时间节点.

在处理实际问题时经常会遇到各种噪声,比如常数噪声(模型误差)、线性动态噪声(偏置误差)、有界随机动态误差(高斯白噪声)等[11].文献[10]提出了如下抗噪声的模型

(2)

其中γ>0,λ>0是两个设计参数.令e(t)=f(x,t)表示问题(1)的残差向量,并将其代入上式得求解问题(1)的抗噪声连续时间ZNN算法

(3)

定理1.1无论未知向量N的分量有多大,抗噪声连续时间ZNN算法(3)的解序列全局收敛于问题(1)的理论解.

由于算法(3)是一个积分-微分模型,一个通常的处理方式是将其化成一个微分方程组,即令

(4)

(4)式仍然是一个微分方程,并且变量的维数增加了一倍.一些经典的求解微分方程数值解的算法,比如龙格-库塔算法,往往需要利用未来时刻节点处的信息,这在一些未来型的时变问题中是不被允许的.因此有必要设计只使用当前时刻节点及其之前节点信息的算法,这也是在离散化连续时间ZNN算法时采用一步前向差商的原因.

2 离散时间ZNN算法

本节将提出一类可以抑制常数的离散时间ZNN算法.首先考虑时刻tk=kτ的带噪声的模型(2),即

(5)

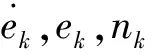
代替；对于右边的定积分,采用复化左矩形公式

于是有

即

(6)

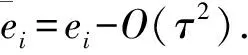
利用(6)式减上式得

(7)

对于常数噪声n(t)≡N∈Rn,(7)式变成了一个齐次线性差分方程,其特征多项式是

h(z)=z2+(-2+γτ)z+(1-γτ+λτ2).

(8)

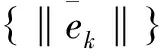
λ>0,4-2γτ+λτ2>0,(γ-λτ)(2-γτ+λτ2)>0.

(9)

证明根据Jury稳定判据,要证明这个结论只需要保证特征方程(8)的根全落在单位圆内即可.于是根据Jury稳定表格,只需要保证

其中ai是(8)式中zi(i=0,1,2)的系数.于是有

h(1)=λτ2>0,

(-1)2h(-1)=4-2γτ+λτ2>0,

b0=τ(γ-λτ)(2-γτ+λτ2)>0.

对上面的不等式组整理即可得本命题的结论.

注2.1满足(9)式的参数是存在的,比如γ=λ=1,τ=0.1.另一方面,γ=25,λ=1,τ=0.1不满足(9)式.

在(5)式中令ek=f(xk,tk),有

(10)

利用上面的差商与复化左矩形公式得第一个离散时间ZNN算法

(11)

其中参数γ,λ,τ满足(9)式.

注2.2由于公式(11)中含有噪声nk,因此其只适用于噪声已知的情况.

由于左矩形公式的截断误差比复化左矩形公式的低一个数量级,下面直接利用左矩形公式来近似定积分.同时对导数采用如下具有二阶截断误差的差商来近似(5)式,即

由于(5)式对下标k-1也成立,于是有

用(5)式与上式相减,得

(12)

利用差商与左矩形公式,(12)式可以写成

整理得

2ek+1+(-5+2γτ)ek+(5-2γτ+2λτ2)ek-1-3ek-2+ek-3=nk-nk-1.

(13)

对于常数噪声n(t)≡N∈Rn,(13)式变成了一个齐次线性差分方程,其特征多项式是

h(z)=2z4+(-5+2γτ)z3+(5-2γτ+2λτ2)z2-3z+1.

(14)

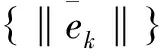
(15)

证明根据Jury稳定判据,要证明这个结论,只需要保证特征方程(14)的根全落在单位圆内即可.于是根据Jury稳定表格,只需要保证h(1)>0,(-1)4h(-1)>0以及Jury稳定表格的第3,5,7行的第一个元素是严格大于零的.经过计算有

对上面的不等式组整理即可得本命题的结论.

注2.3满足(15)式的参数是存在的,比如γ=λ=1,τ=0.1.另一方面,γ=11,λ=1,τ=0.1不满足(15)式.

根据上面推导参数范围的步骤,我们可以得到另一个离散时间ZNN算法.因为(10)式对下标k-1也成立,于是有

(16)

利用(10)～(16)得

当n(t)≡N∈Rn时,利用上面的差商与左矩形公式得第二个离散时间ZNN算法

(17)

其中参数γ,λ,τ满足(15).

注2.4与文献[11]中提出的抗噪声离散时间ZNN算法不同,本文提出的算法(11)与(17)的变量个数没有增加.同时利用右矩形公式可以得到类似的离散时间ZNN算法.

下面讨论在未知线性噪声n(t)=at+b∈Rn环境下的离散时间ZNN算法.此时,(7)式变成

同理有

上两式相减得

(18)

其特征多项式是

h(z)=z3+(-3+γτ)z2+(3-2γτ+λτ2)z-(1-γτ+λτ2).

(19)

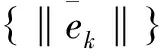
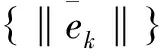
注2.5定理2.3的结论与文献[10]里的结果是相对应的.对于抗线性噪声的连续时间ZNN算法[10]，证明了其产生的稳态误差与其设计参数成反比,因此只有当设计参数趋于正无穷时,稳态误差才趋于零.

最后来讨论具有三阶截断误差的梯形积分公式是否可以生成收敛的离散时间ZNN算法. 同时对导数采用如下具有三阶截断误差的差商来近似[12]

将上面的差商与梯形积分公式代入(12)式得

-γek+γek-1-λτek-1+nk-nk-1，

整理得

同样地,对于常数噪声n(t)≡N∈Rn,上式变成了一个齐次线性差分方程,其特征多项式是

h(z)=11z5+(-11+24γτ)z4+(-6-24γτ+24λτ2)z3-2z2+11z-3.

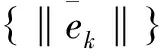
证明根据定理2.1的证明过程,容易得到本定理的结论成立.

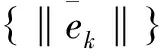
由此可以得到第3个离散时间ZNN算法

(20)

其中γ=1,λ=1,τ=0.1或0.01.

3 数值实验

本节给出3个数值实验来验证所提离散时间ZNN算法的有效性.将离散时间ZNN算法(11),(17),(20)分别记为DT-ZNN1,DT-ZNN2,DT-ZNN3,并将文献[11]中的离散时间ZNN算法记为DT-ZNNQ.

问题1考虑单变量时变非线性方程

f(x,t)=2x+sin(x)-t,t∈[0,20].

显然该时变非线性方程问题在每个时刻点都是有解的.我们先使用DT-ZNNQ求解该问题,目的是为了说明当参数取的不合适时,DT-ZNNQ可能是发散的.噪声n(t)≡1,初始条件均设为0,参数h=0.1,ρ=1或10,实验结果见图1,其中纵坐标表示残量,定义是(Res)k=‖fk‖.

图1 DT-ZNNQ求解问题1的结果(左：ρ=1,右：ρ=10)

由图1的两个子图可以看出,当ρ=1时DT-ZNNQ收敛,但是当ρ=10时DT-ZNNQ发散,因此当设计参数取的不合适时,DT-ZNNQ可能是发散的.下面我们利用DT-ZNN1来求解问题1,初始条件x0=0,实验结果见图2,其中γ=λ=1，τ=0.1.

由图2可以看出,当参数γ,λ,τ满足(9)式时,DT-ZNN1是收敛的. 注2.1指出γ=25,λ=1,τ=0.1不满足(9)式,此时DT-ZNN1应该是发散的,这与图3的观察是一致的.

图2 DT-ZNN1求解问题1的结果 图3 DT-ZNN1求解问题1的结果(γ=25,λ=1,τ=0.1)

问题2考虑时变线性方程组问题

初始条件均设为0,参数γ=λ=1,τ=0.1，实验结果见图4.

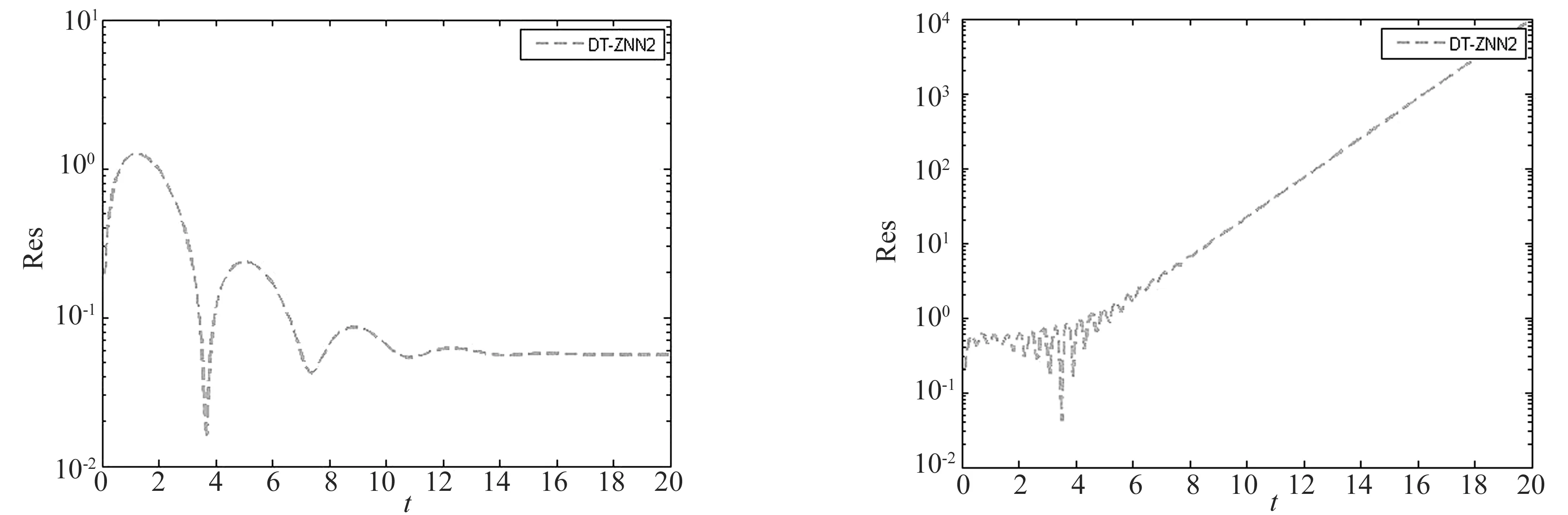
图4 DT-ZNN2求解问题2的结果 图5 DT-ZNN2求解问题2的结果(γ=11,λ=1,τ=0.1)

由图4可以看出,当参数γ,λ,τ满足(15)式时,DT-ZNN2是收敛的.注2.3指出γ=11,λ=1,τ=0.1不满足(15)式,此时DT-ZNN2应该是发散的,这与图5的观察是一致的.

问题3考虑时变非线性方程组问题

我们利用DT-ZNN3求解这个问题,参数γ=λ=1，τ=0.1,初始值均取为零,求解的结果显示在图6中.

由图6可以看出,当参数γ=λ=1,τ=0.1时,DT-ZNN3是收敛的. 注2.6指出当γ=10,λ=1,τ=0.1时,DT-ZNN3应该是发散的,这与图7的观察是一致的.

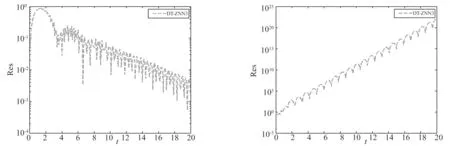
图6 DT-ZNN3求解问题3的结果 图7 DT-ZNN3求解问题3的结果(γ=10,λ=1,τ=0.1)

4 总 结

本文对常数噪声下的离散时间ZNN算法进行了研究,提出了3种离散时间ZNN算法.本文的一个最大成果是对噪声环境下的离散时间ZNN算法的参数研究提供了一种系统的研究思路,按着这个研究思路可以提出更多的具有收敛性质的离散时间ZNN算法.下一步的研究方向包括：(1)研究线性噪声或随机有界噪声下的离散时间ZNN算法. (2)借助于具有更高阶的数值积分方法,研究具有更高精度的离散时间ZNN算法.