基于格子玻尔兹曼方法的二维柔性梁与刚性方柱相互作用的数值研究
杨旖旎,谢振武,邹明松
(中国船舶科学研究中心,江苏 无锡 214082)
0 引 言
带流固耦合的复杂绕流,尤其是柔性体-刚体-流体耦合运动,在自然界中普遍存在,如鱼类在海洋立管前后端的游动,以及日常生活中所见到的旗帜拍动等。柱体后加柔性丝线的流固耦合振动是流固耦合研究中的典型问题。Sui 等[1]对静止圆柱尾流与无质量柔性丝线的耦合干扰进行了数值模拟;Yildirim 等[2]发现了丝线运动方式对上游圆柱尾流的反馈影响;Jia 和Yin[3]通过肥皂膜流动的实验发现,随着丝线相对圆柱的位置变化,柔性丝线在尾流中呈现出三种典型的拍动响应模态;胡浪超等[4]采用罚浸入边界/格子Boltzmann方法研究了旋转圆柱尾流中的柔性丝线拍动模态。
与圆柱体后加柔性体的流固耦合问题相比,方柱后加柔性体的文献记载更少。对于方柱振动问题,Bearmann 等[5]针对风洞中的方柱进行了实验研究。Coeless 和Parkinson[6]发展了拟稳态模型,模拟了方柱振动,并与实验进行了对比。Zhao 等[7]数值模拟了低雷诺数下带流向角的单方柱振动问题,研究发现:当流向角为0°时单方柱并无驰振现象,且锁定区域较小;当流向角为22.5°和45°时有驰振,且锁定区域明显增大。Sharma和Dutta[8]通过实验分别对带有刚性和柔性板的固定方柱的流场结构特征进行了研究,发现板长的改变将引起尾迹的明显转变。涂昌健等[9]基于浸入边界-谱元法数值模拟了方柱附加柔性悬臂梁流固耦合振动问题。
以往学者对于圆柱体后加柔性体的流固耦合问题较为关注,但是对低雷诺数下,方柱后附加柔性体的研究较少。为了进一步研究方柱后附加柔性梁对方柱振动的影响,本文对雷诺数Re=100 时,方柱质量比mr=3,梁质量比ms=0.3,弯曲刚度系数kb=0.0001时的方柱后附加柔性丝线的流致振动进行了数值研究,重点研究了方柱的振动幅值、振动频率等振动响应特性随折减速度的变化规律。
1 控制方程及其求解
1.1 格子波尔兹曼方法(Lattice Boltzmann Method,LBM)
与传统CFD(Computational Fluid Dynamics)直接求解宏观N-S(Navier-Stokes’)方程不同,LBM 通过求解离散玻尔兹曼方程:
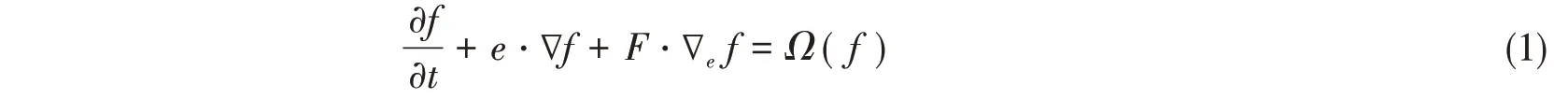
得到流体的运动,是一种介观方法。其中e为粒子速度,Ω(f)表示粒子的碰撞。
在LBM 中,流体被看成是规整格子上的流体粒子,用粒子分布函数fα表示,流体粒子按α个特定方向的粒子速度进行迁移和碰撞演化,最终得到所需要的流场信息。基于迁移和碰撞这一求解特性,LBM 具有计算简单、并行效率高、边界处理容易且易于耦合复杂外力场等优点。LBM 中的离散速度模型一般记为DdQm模型,其中d表示维度,m表示离散速度数量。本文对二维数值研究采用了D2Q9模型(二维九速度模型),如图1所示。

图1 D2Q9模型Fig.1 D2Q9 model
选取单松弛碰撞模型Ω(f)= -(f-feq)/λ,通过离散方程(1)可得格子玻尔兹曼方程:
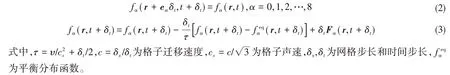
式(3)中,力项F采用Guo[10]等人提出的外力格式:
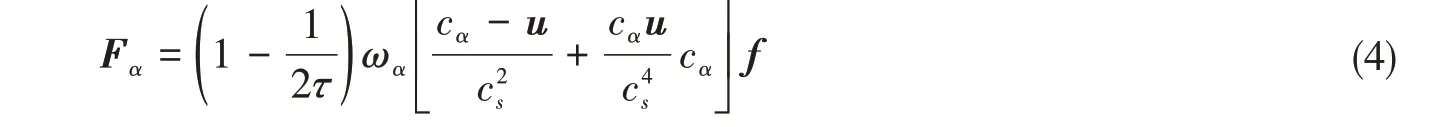
通过对分布函数求零阶和一阶矩,可得流体的宏观密度、速度与压力分别为
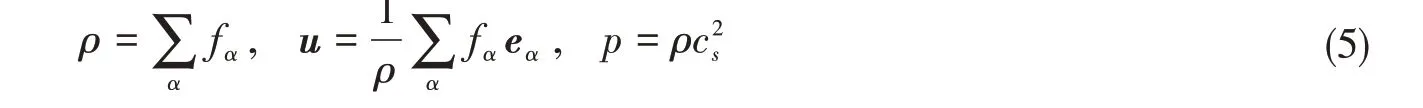
1.2 固体控制方程与数值方法
以流体密度ρ、来流速度U、梁长Lf为基本参考量,可得到柔性梁在拉格朗日网格下的控制方程:
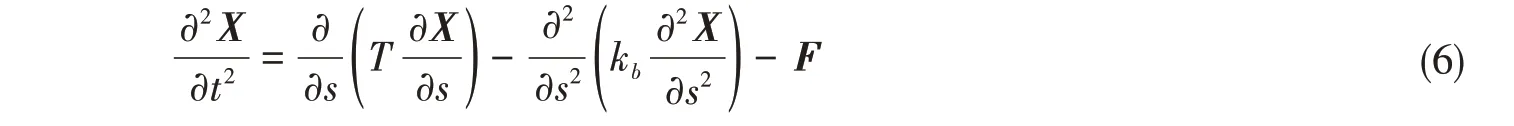
对于第i(i= 0,1,2,...,n)个节点,张力项T可离散为
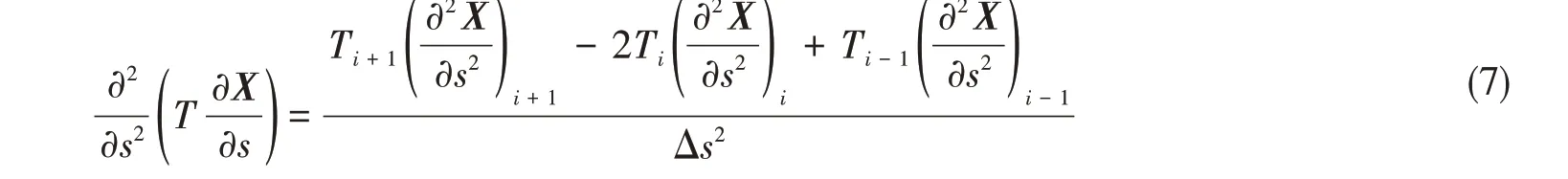
张力T由不可伸长条件确定,具体可参考文献[11]。将T代入式(6)则可得到更新的梁位置坐标及速度。
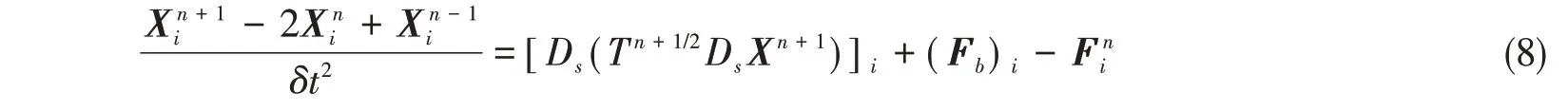
以流体密度ρ、来流速度U、方柱宽度D为基本参考量,单方柱运动控制方程可表示为

1.3 边界处理
对于流固耦合边界采用浸入边界法处理。欧拉点上的速度传播到附近拉格朗日固体点上的过程可表示为

拉格朗日力传播到附近流体欧拉点上的过程可表示为
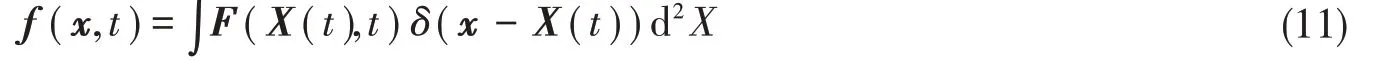
1.4 时间异步算法

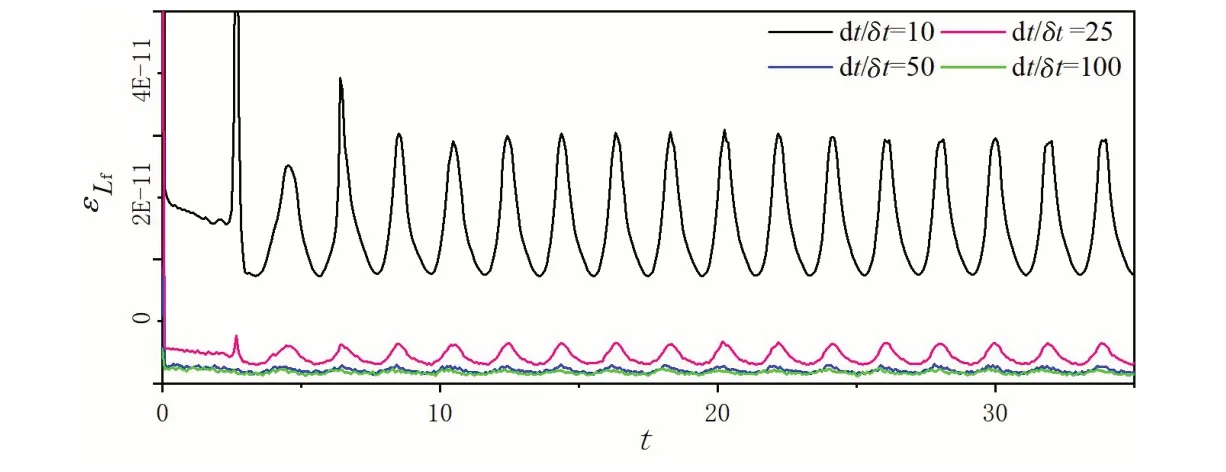
图2 时间步长比值随时间的误差变化Fig.2 Variation of time step ratio with time error
图2中,dt为流体域所取时间步长,δt为结构域所取时间步长。由图可以看出,当流体域步长与结构域步长比为50、100 时,计算误差结果基本无差别。考虑到计算精度及计算效率的情况下,本文取时间异步算法的比值为dt/δt= 50。
2 计算参数设置以及数值验证
2.1 计算参数设置
图3 为方柱后附加柔性梁模型的简化示意图,入口给定一恒定速度U的均匀来流,雷诺数定义为Re=UD/υ。本文采用均匀网格,网格大小为0.02D,入口及上下边界条件采用远场边界条件u=U,v= 0,出口边界条件定义为纽曼边界条件,即密度、速度沿轴向的梯度满足∂u/∂x= ∂v/∂y= 0。选取计算域大小为[L×H]=[60D×24D],此时边界对计算结果影响可以忽略不计。方柱中心固定在[L/3,H/2]处。为了防止方柱与柔性梁发生碰撞,柔性梁固定端到方柱中心的距离G= 6D。
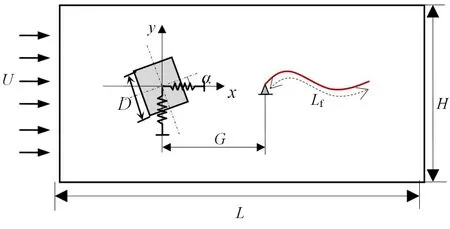
图3 方柱-柔性梁系统结构示意图Fig.3 Schematic diagram of square cylinder-flexible beam system
2.2 数值验证
为了验证本文计算方法的可靠性,本文对雷诺数Re= 100,质量比mr= 3,流向角为45°的单方柱振动进行了数值模拟。Ymax=(Ay,max-Ay,min)/2 分别为方柱的顺流、横向无量纲振幅,其中Ay,max,Ay,min为方柱的最大位移和最小位移,fx,fy,fn分别为方柱顺流向、横向振动频率及固有频率。结果如图4所示,本文计算结果与文献[7]的结果吻合良好。

图4 方柱流致振动结果验证Fig.4 Verification of flow induced vibration results of square cylinder
为了与已有文献结果作对比,本文对雷诺数Re= 100,kb= 0.0001,ms分别为0.22和0.28的梁拍动进行数值模拟。由图5可以看出:当质量比为0.22时,柔性梁在平衡位置附近震荡后,幅值逐渐减小,最终达到静止模态;当质量比为0.28 时,柔性梁为稳定的周期性拍动。因此,柔性梁由稳定状态到失稳的临界比在0.22~0.28之间,这与文献[12]中ms= 0.26相吻合。

图5 梁自由端位移时程曲线Fig.5 Displacement of a beam with free end position versus nondimensional time
3 结果与讨论
3.1 方柱振动响应特性
对低雷诺数下Re= 100,D= 50,mr= 3,α= 45°,kb= 0.0001,ms= 0.3,Lf= 2D,G= 6D的方柱-柔性梁耦合系统进行数值模拟。为了防止方柱横向位移过大与柔性梁发生碰撞,选取折减速度ur=3~17进行了模拟,对于每一种情况,都进行了足够长的模拟时间以确保振动达到平衡态。
图6为方柱的XY轨迹图,图7为方柱无量纲振幅Ymax=(Amax-Amin)/2和振动频率比f=f/fn随ur的变化曲线。由图6~7可以看出:
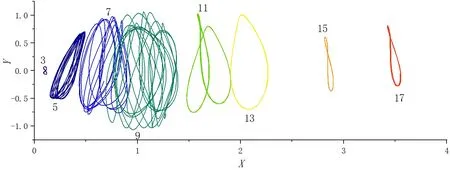
图6 XY轨迹图Fig.6 XY-trajectory
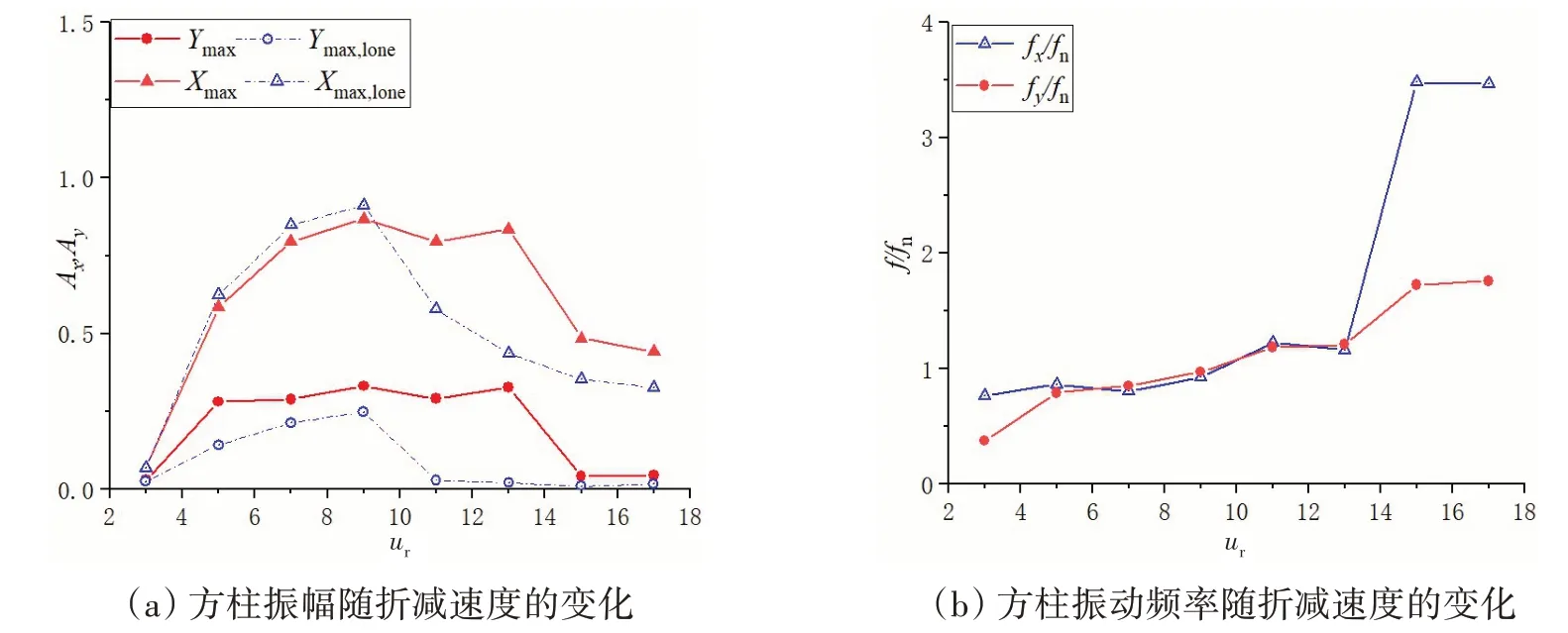
图7 方柱振动响应特性Fig.7 Response of the square cylinder with ur
(1)在锁定区内(3<ur<13),当ur<11时,由于振动的不规则性,导致XY轨迹为非闭合环,随着ur的增加(ur≥11),由闭合的双相环逐渐发展为闭合单相环;在振动锁定区外(ur<5,ur>13),当ur较小时(ur<5),为对称的‘8’字型单相环,当ur较大时(ur≥15),发展为不对称的‘8’字单相环。
(2)方柱下游附加梁的振动依然以横流为主,这与单方柱的振动类似。对任意梁长,随ur的增加,方柱均出现了明显的振动锁定区,且锁定区域大于单方柱情况下。
(3)在振动锁定区内,方柱的X、Y方向振动频率比基本相等,且在1附近,在振动锁定区外,X方向频率比约为Y方向的两倍。
图8为不同折减速度下,方柱振动的位移时程曲线。当ur=5~11,方柱做明显的不规则振动;当ur=13~15,方柱出现周期性振动,此时振动频率接近于方柱的固有频率,这是导致其振幅较大的主要原因;在ur=3,17时,方柱出现周期性振动,且振幅较小(<0.5),X方向的振动频率约为Y方向的两倍。
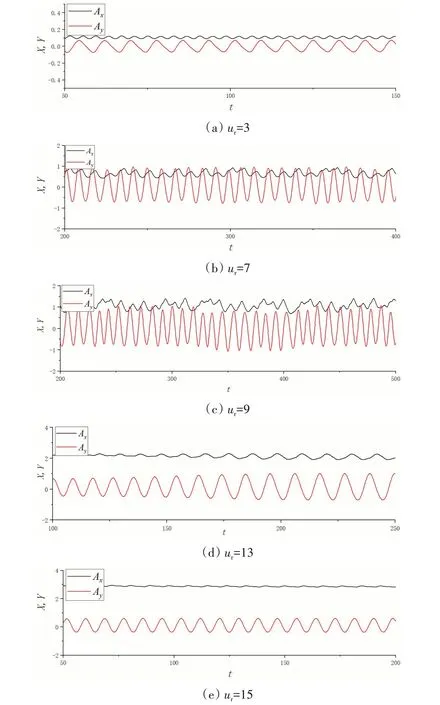
图8 方柱位移时程曲线Fig.8 Time histories of vibration displacement at different reduced velocities
图9给出了方柱能量输入、升力系数及横向位移的时程曲线,其中Py=Cl,s(t)v(t)/U为方柱的无量纲功率。在振动锁定区域外(图9(a)、(e)),方柱的位移及升力系数随时间推移呈稳定的变化趋势,且相位相反,此时升力对方柱的能量输入稳定。在振动锁定区域内,方柱平均升力系数不为零,此时方柱发生驰振(图9(b)、(c)),位移与升力系数相位一致,方柱源源不断地从外界吸收能量;在驰振区外(图9(d)),方柱位移及升力系数呈稳定的周期性变化,外界对方柱能量输入稳定,由于此时方柱振动频率接近固有频率,升力极易激励方柱振动,致使方柱横向产生较大位移。
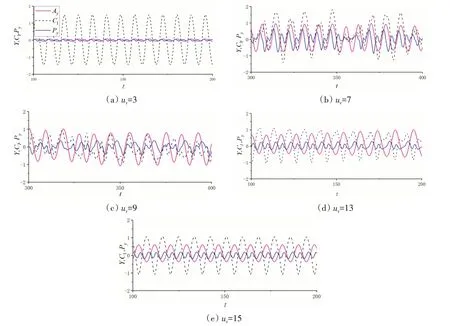
图9 方柱横向位移、升力系数、能量输入时程曲线Fig.9 Time histories of the lateral displacement,lift coefficient and energy input
3.2 流动结构特征
图10分别给出了在方柱最大位移,ur= 3~17时的瞬时涡量图。由图可以看出系统的间距流态主要分为三种:
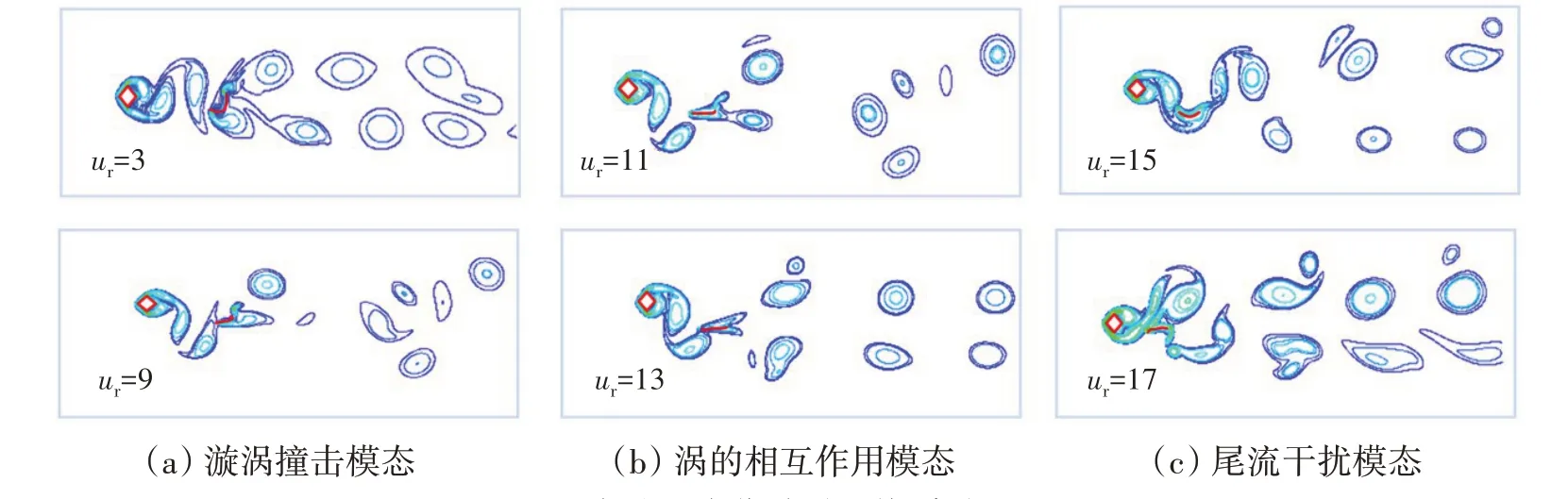
图10 方柱最大位移时系统瞬时涡量图Fig.10 Instantaneous vorticity graph of the system at the maximum displacement of the square cylinder
(1)旋涡撞击模态。上游方柱上下剪切层交替卷起形成旋涡并向下移动,当与柔性梁主体发生碰撞时,撞击使得下游柔性梁产生较大的脉动升力,使其自由端产生较大位移;与此同时,上游方柱产生的旋涡被截断,截断后的部分子涡分别与柔性梁自身的尾涡发生合并,并以涡对形式向下脱落;
(2)涡的相互作用流态。此时上游产生的旋涡不再撞击下游柔性梁,而是与下游柔性梁下侧产生的旋涡耦合产生相互作用,上游方柱受下游柔性梁的干扰较小,下游柔性梁振动则受到上游方柱涡脱的抑制;
(3)尾流干扰流态。此时,由于上游方柱顺流位移较大,导致方柱与柔性梁间距较小,上游方柱上侧剪切层再附到柔性梁表面,使得柔性梁完全沉浸在上游方柱的尾流中。
3.3 旋涡形成与脱落
图11 展示了折减速度ur=9 时,在一个振动周期内,方柱横向振动位移Ay与柔性梁自由端横向位移By的时程曲线及系统在点A、B、C、D的瞬时涡量图,此时间距流态为漩涡撞击模态,方柱与柔性梁自由端振动相位为反相位。在方柱的一个振动周期内,方柱上侧分离出一个涡在上行向后运动,下侧分离出两个涡,其中一个在下行向后运动并与柔性梁发生碰撞,另一个在上行向后运动,系统尾涡不规则。
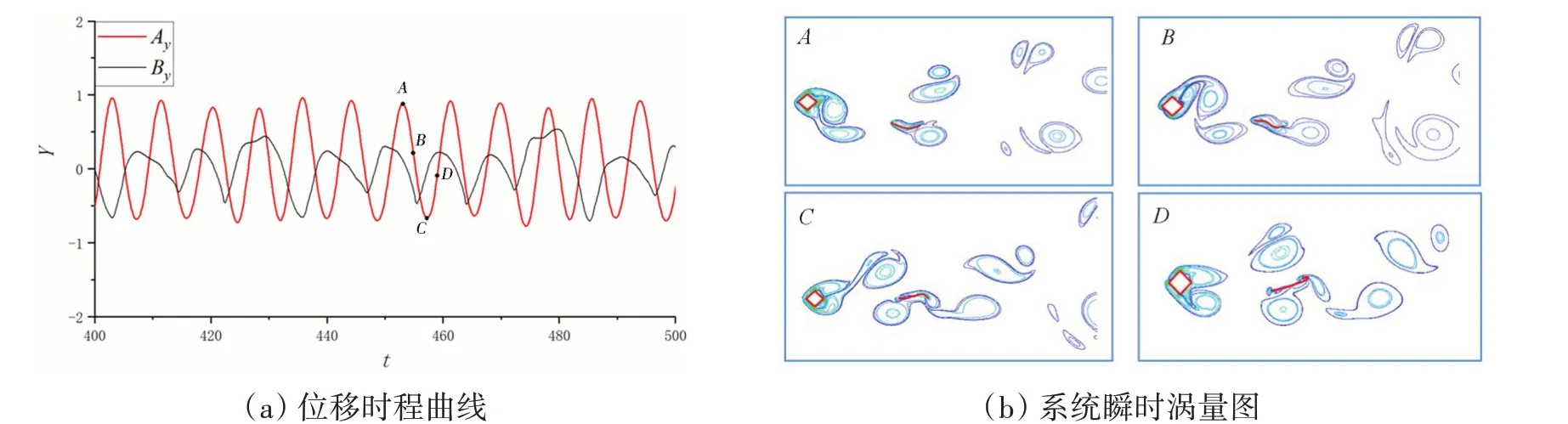
图11 ur=9时系统的振动响应Fig.11 Vibration response of the system at ur=9
图12 展示了折减速度ur=13 时在一个振动周期内系统的位移时程曲线及瞬时涡量图,此时方柱与柔性梁自由端振动相位为同相位。此时方柱涡脱与ur=9类似,但系统尾涡呈‘2P’模式。

图12 ur=13时系统的振动响应Fig.12 Vibration response of the system at ur=13
图13 展示了折减速度ur=17 时,在一个振动周期内系统的瞬时涡量图,此时间距流态为尾流干扰模态,方柱处于振动锁定区外。对于单方柱振动,在一个振动周期内涡脱数量为偶数,且强度相等,方柱形成的XY轨迹也是对称的‘8’字型轨迹。受下游柔性梁的影响,方柱每个振动周期内有两个旋涡脱落,旋涡在未完全脱离方柱时,便附着到柔性梁上,此时,上涡与下涡强度不一致,这也是导致柔性梁振动不对称的主要原因。
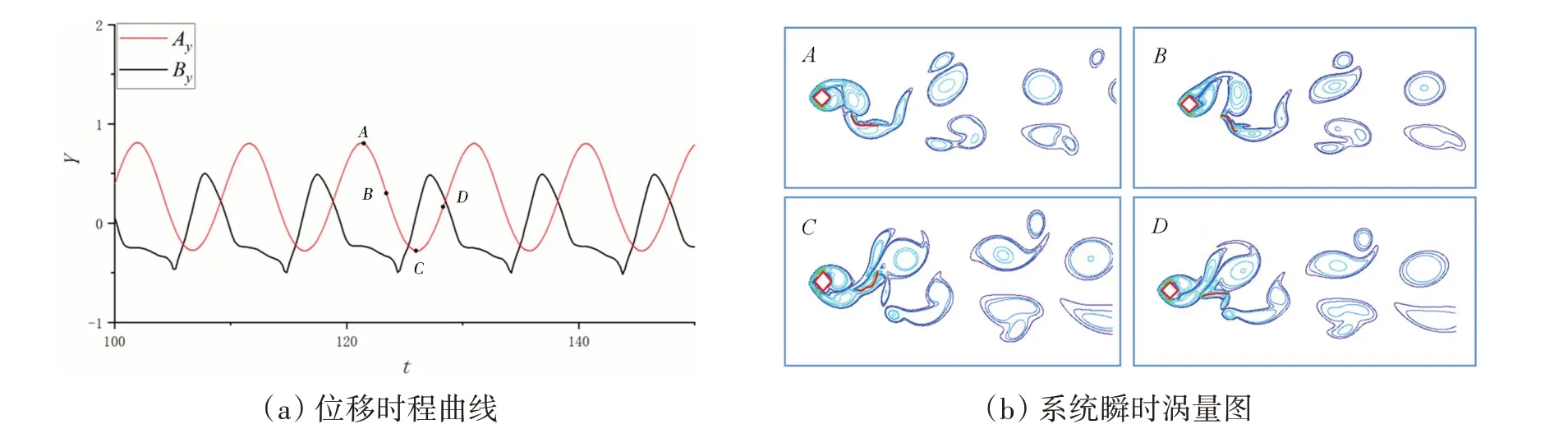
图13 ur=17时系统的振动响应Fig.13 Vibration response of the system at ur=17
4 结 论
本文基于IB-LBM方法提供了一套求解刚体-柔性体耦合系统流固耦合的计算方法。首先通过计算单方柱、单柔性梁的流致振动验证程序在计算刚体-柔性体-流体耦合系统绕流问题时的可靠性。结果表明,本文提出的结合时间异步算法的多步直接力-格子Boltzmann 方法,能很好地处理刚体-柔性体-流体耦合系统的流固耦合问题。然后对低雷诺数(Re=100)下带流向角α=45°方柱后附加柔性梁的流致振动进行了研究,发现带柔性梁的方柱振动与单方柱振动具有显著的区别,并得到如下结论:
(1)从计算结果上来看,柔性梁的模拟结果与已有文献可以很好地吻合,表明了本文采用的方法可以很好地模拟柔性结构流固耦合问题;
(2)方柱下游附加梁的振动依然以横流为主,随着折减速度ur的增加,方柱均出现了明显的振动锁定区,对任意柔性梁长度,锁定区域均大于单方柱情况下。在振动锁定区域内存在两种振动状态,当ur较小时,主要是平均升力系数不为零而导致的驰振,当ur较大时主要是由于振动频率接近于固有频率而导致的振幅较大;
(3)系统随折减速度变化共出现了3种间距流态:尾流干扰、旋涡撞击及涡的相互作用流态。
未来将对高雷诺数下带流向角的方柱后附加柔性梁的流致振动进行模拟,并将结果与COMSOL软件计算所得结果进行比较,做进一步验证。

