序贯压缩感知下的海洋监测数据在线重构方法
刘 歌,芮国胜,田文飚,田润澜,王晓峰
(1.海军航空大学 信号与信息处理山东省重点实验室,山东 烟台 264001;2.空军航空大学 作战勤务学院,吉林 长春 130022)
蒸发波导既能陷获无线电波,有助于实现超视距传播,又可能造成频谱泄露,导致己方目标过早暴露,在海洋电磁空间中发挥的作用不容小觑。蒸发波导信息的高效感知有赖于温度、湿度、压强、海表温度以及风速信息的全面准确获取[1]。由于卫星遥感以及雷达等手段获取的数据尺度范围太大,分辨率过低,因此传感器网络成为获取海洋环境监测数据的主要手段[2]。现实场景中,在某一海洋监测区域内通过部署多个传感器构成传感器网络,对同一对象进行持续的感知,获取多种环境监测数据通过某种通信手段传送到监测中心,以支撑不同类型的感知应用[3-5]。与陆地环境相比,海洋环境在深度和广度上都具有优势,但这一优势对海上传感器网络的部署提出了更高的要求:一方面海洋范围过大,导致部署节点数量太多,使得建设成本过高;另一方面如何将采集到的大量信息及时有效传输也受到节点能耗以及通信成本的限制。这就决定了传感器网络在运行过程中必须找到一种合理的方案解决能源有限与数据传输之间的矛盾。
压缩感知(Compressed Sensing,CS)的出现为解决上述问题提供一个新的思路。BAJWA等[6]提出将压缩感知理论引入到传感器网络的高效数据采集问题中,自此之后,学者们开始将压缩感知理论在传感器网络中的应用进行大量研究。LUO等[7]提出基于压缩感知的压缩数据采集(Compressive Data Gathering,CDG)算法。在该算法中,Sink节点接收到的数据为每个节点数据的加权和,有效减少了网络中总的传输次数,减少了通信能耗,其副作用就是使得各节点的发送量增多;文献[8]和文献[9]对传感器网络的观测矩阵进行了改进并分析;WU等[10]为降低观测矩阵的稀疏度,每轮数据收集时仅有1个节点参与,每个数据收集周期仅有M个节点发送数据,极大地减少了节点通信能耗开销。但是上述算法都没有将传感器网络数据收集过程中动态变化产生的相关性考虑在内。近年来,动态压缩感知(Dynamic Compressed Sensing,DCS)旨在处理信号支撑集随时间发生变化的时变稀疏信号[11-14],目前已经在研究时间流信号的采集和重构方面取得了很多有价值的研究成果[15-18],但是现有的动态压缩感知算法仍是基于时间域上的压缩观测,并未涉及其他域压缩。例如文献[19]中的渐进式信号重构的顺序压缩感知(Sequential Compressed Sensing with Progressive signal reconstruction,Seq-Prog-CS)算法就是在动态压缩感知的思想上提出的;该算法是对传感器数据流的顺序压缩采集和渐进重构,然而在传感器时间序列数据收集过程中,只考虑了时域流信号前后时刻的动态演化关系,没有考虑多传感器之间的空间结构相关性,重构性能有待提高。事实上,多个传感器在时间上不断地进行观测,相当于是时域流信号的多传感器扩展。
针对上述问题,笔者对实际海洋监测数据进行了分析,发现传感器数据矩阵空间结构上的低秩性。利用滑动窗口机制,结合已有历史数据,构建低秩矩阵,充分利用矩阵的低秩性,提出基于低秩正则化的序贯压缩感知重构算法(Sequential Compressed Sensing based on Low rank Regularization,Seq-CS-LR),同时根据重叠区域数据相等的规律,增加了重叠区域误差校正项。在解决重构优化算法过程中设计了一种基于交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)的求解方法。实验结果验证了算法获得了更高的重构精度。
1 序贯压缩感知
某时刻N个传感器获得的数据x=(x1,x2,…,xN)∈RN,通常可以在稀疏表示矩阵Ψ∈RN×N下可以被稀疏表示,即x=Ψs,此时s中若至多存在k个非零元素,则将x称为可压缩数据,k表示稀疏度,s表示数据x在稀疏表示矩阵下的稀疏表示系数向量。
假设观测矩阵为Φ∈RM×N,根据压缩感知理论,测理值y可以被表示为
y=Φx=ΦΨs,
(1)
其中,M≪N;A=ΦΨ,表示感知矩阵。
图1给出了滑动窗口数据采集示意图,从图中可以看出,随着时间的推进,在滑动窗口内,新时刻数据进入的同时,旧时刻的数据被推出,即相邻时刻滑动窗口内的矩阵之间存在着重叠区域。每个滑动窗口包含w个时间间隔,但并非所有数据窗口都需要在每个时间间隔发送。首先,用w个时间间隔的历史数据集作为原始数据窗内的初始化数据,当下一个时刻的数据集合进入时,旧时刻的数据集将被推出。因此,在第t个时隙仅发送具有M(t)/w维度的数据集,M(t)表示第t个时隙的观测数目。序贯压缩感知具体的观测过程见图2所示。具体可以表示为
(2)
其中,φ(t)∈RM(t)/w×N,表示t时刻的观测矩阵。
据图中的描述,当x(t)进入时,x(t-w)退出,这样保持了上述公式形式不变,但是实际内容在不断地随时间的推进而更新,从而实现数据的在线采集。可以将式(2)写成矩阵形式为
Y(t)=Φ(t)v(X(t)) ,
(3)
其中,X(t)∈RN×w,表示窗口内的数据矩阵;v(·)表示向量堆栈;Φ(t)∈RM×Nw,表示窗口w内的块对角观测矩阵的集合;Y(t)=[yT(t-w+1)yT(t-w+2)…yT(t)]T∈RM×1,表示窗口w内的测量向量的集合;M=∑M(t),表示窗口内观测值的总数。
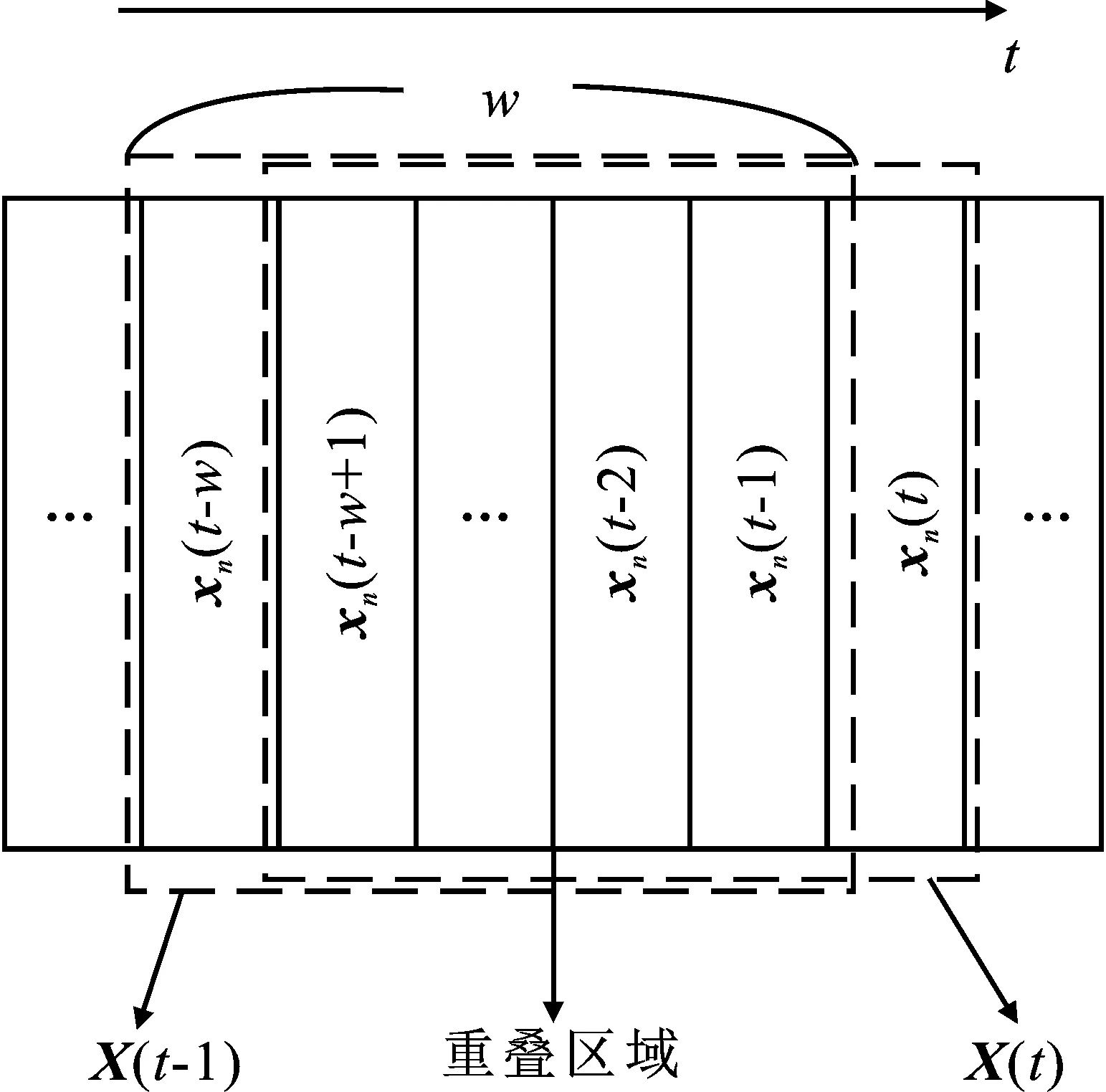
图1 滑动窗口数据采集示意图
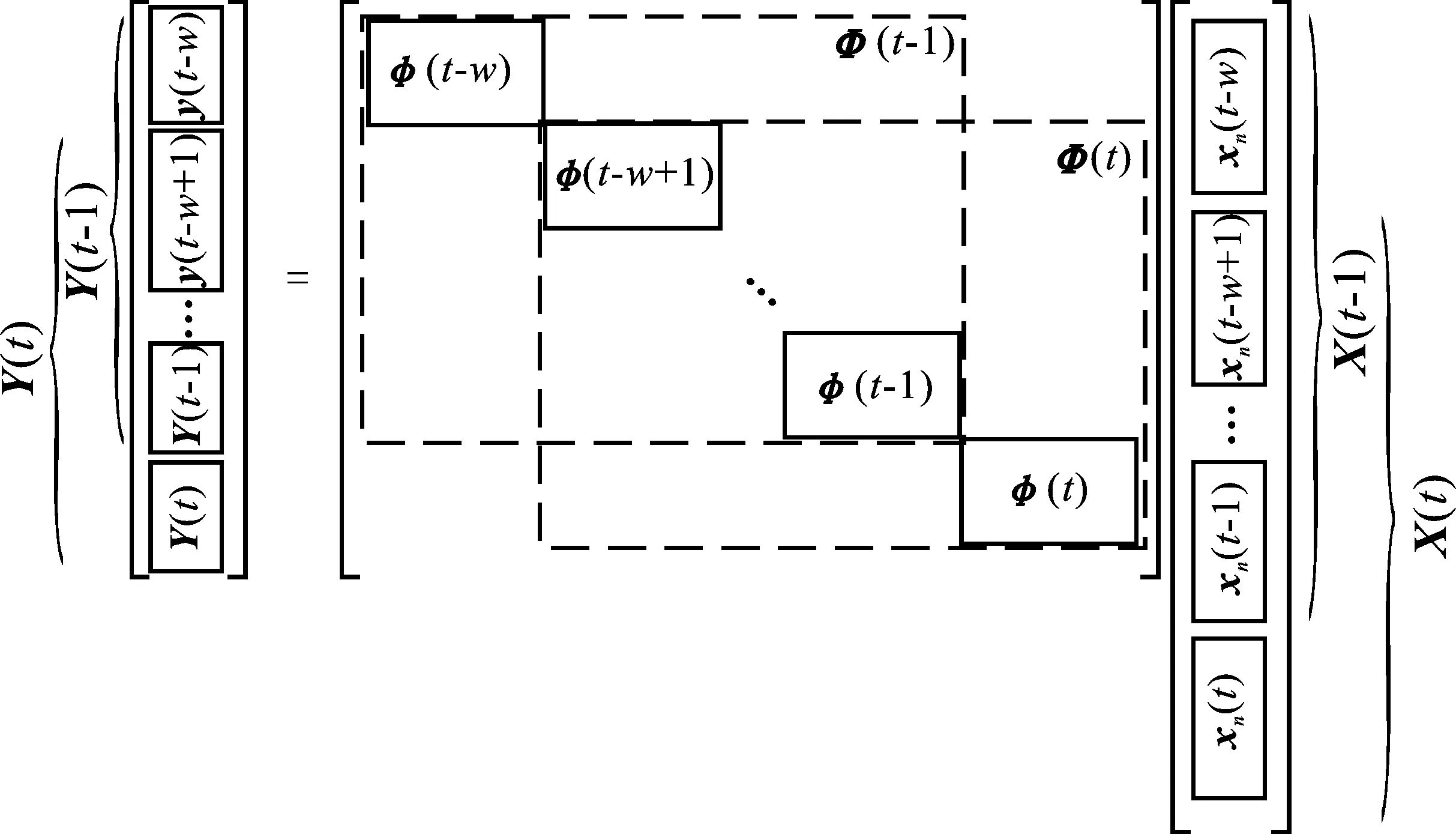
图2 序贯压缩感知观测过程示意图
1.1 联合压缩感知和矩阵低秩性的数据重构
传统的序贯压缩感知观测模式将滑动窗口内的矩阵堆栈为向量进行计算,没有对滑动窗口内矩阵的结构特性进行研究。事实上,滑动窗口矩阵的列向量是来自相同传感器在不同时隙内的数据,且海洋环境监测数据在大范围内变化缓慢,这就意味着列向量之间存在着大量的冗余,因此考虑加入低秩约束以更好地利用滑动窗口内矩阵的低秩性来提高重构性能。
首先,为了检验滑动矩阵X(t)∈RN×w是否具有良好的低阶近似,采用奇异值分解(Singular Value Decomposition,SVD)的方法,即
X(t)=UΣVT,
(4)
其中,U∈RN×r,表示传感器源隐含因子矩阵;V∈Rw×r,表示时间序列隐含因子矩阵;Σ∈Rr×r,为对角阵,对角元素是矩阵X(t)奇异值;r表示矩阵X(t)的秩,当矩阵的秩满足r≪min{N,w}时,矩阵为低秩矩阵。定义一个变量η来确定矩阵是否具有良好的低秩近似,η通过计算前k个大奇异值的能量之和占所有奇异值的总能量的比值而来,即
(5)
其中,σi表示矩阵的第i个奇异值。
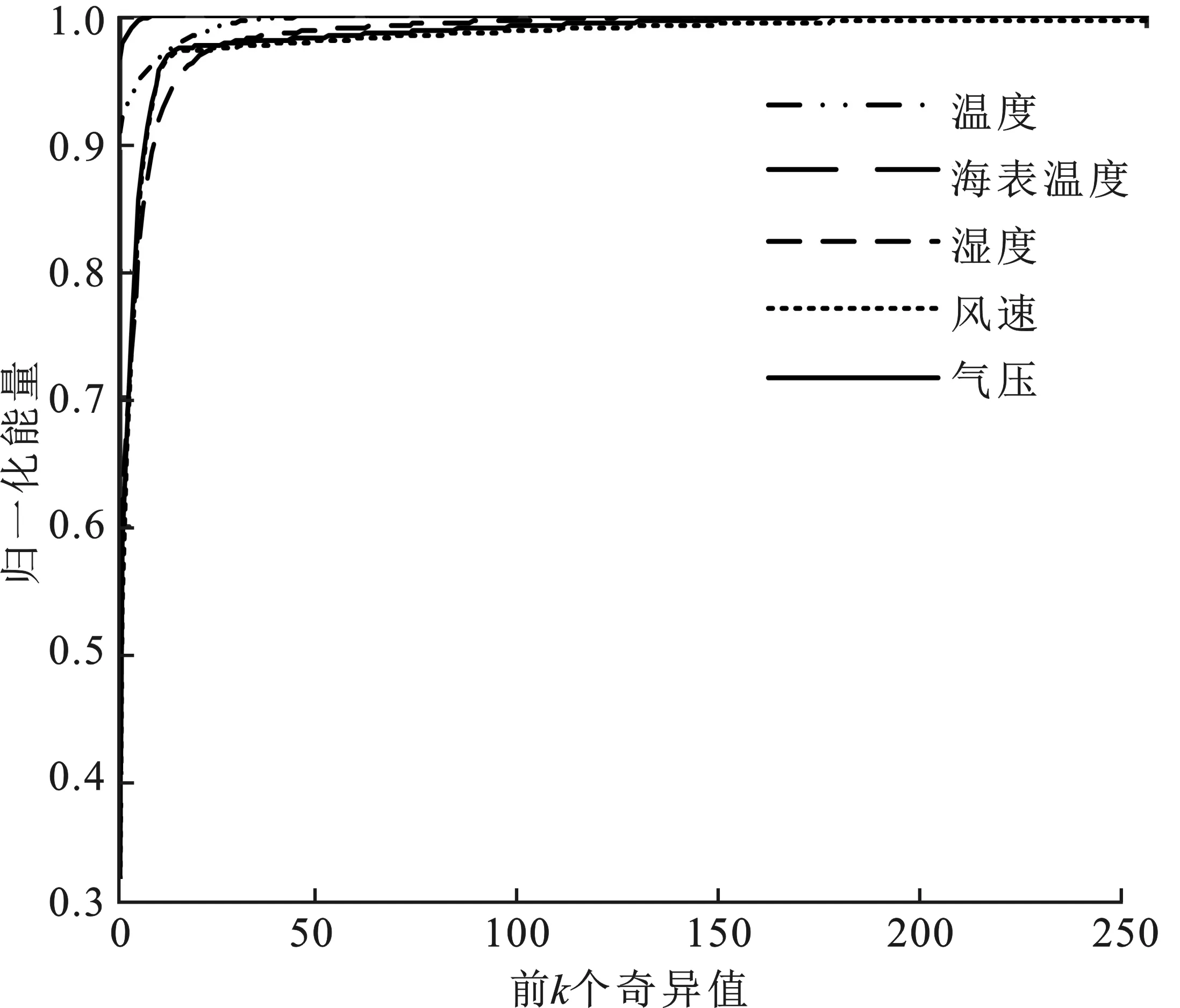
图3 前k个奇异值捕获能量比值的累积分布图
下面对来自美国国家环境预报中心(National Center Environment Prediction,NCEP)中的实测数据进行分析。限于篇幅,仅对蒸发波导特性研究所需要的气温、风速、海表温度、压强、相对湿度5种环境要素进行分析。NCEP数据集的时间分辨率为6 h(一天内更新时间为0∶00,6∶00,12∶00,18∶00),空间分辨率为2.50×2.50。图3中给出了5种气象要素数据的前k个大奇异值能量占总奇异值能量的比重,其中横坐标为k,纵坐标表示前k个大奇异值之和占奇异值总和的比重。本次数据是每个传感器节点在感兴趣的时间范围内产生的256个采样点。从图3的整体来看,5种海洋数据的前10个奇异值之和已占奇异值总和的90%以上。对于温度和海表温度两个参数,前10个系数所捕获的能量甚至达到96%以上。上述结果完全可以表明5种海洋环境监测数据的矩阵在所研究的场景中具有良好的低秩性。
式(3)中的信号重构是一个病态的逆问题,常用的重构优化算法模型为
(6)
由于t时刻与t-1时刻的时间窗内的存在重叠区域,利用重叠区域内数据相等的先验,增加一个具有数据保真作用的正则化项,以进一步提高重构精度,即
(7)
其中,Ψ(w-1)=ΨT(w-1)ΨS,ΨT(w-1)表示取时域基ΨT的前w-1行组成的新矩阵;X0(t-1)表示t-1时刻计算获得的重叠区域的估计值;S(t)表示稀疏表示系数。
根据前文对滑动窗口内数据矩阵的低秩先验分析,为了进一步提高恢复精度,考虑实施一个有效的低秩性惩罚函数,以充分利用数据之间的空间结构相关性。因此,引入多节点时间序列数据的低秩性惩罚项,得到
(8)
其中,λ1和λ2表示正则化参数,‖X‖表示矩阵X的核范数。
对于式(8),采用交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)将原问题分为多个子问题分别进行解决。首先进行变量替换:
(9)
将上式写成增广拉格朗日的形式:
(10)
其中,A和B表示拉格朗日乘子,α和β是罚参数。通过以下交替方向方法最小化等式(10):
(11)
(12)
(13)
Ak+1=Ak+α(Sk+1(t)-Ψv(Xk+1(t))) ,
(14)
Bk+1=Bk+β(Zk+1(t)-Xk+1(t)) 。
(15)
式(11)可重写为标准线性最小二乘问题,并应用共轭梯度算法求解:
(16)
上述问题是一个标准的最小二乘问题,其最优解可以表示为
(17)
对于式(12)中的子问题,整理得到
(18)
式(18)是标准线性最小二乘问题,Sk+1(t)的求解方法与式(16)相同。
对于式(13)中的子问题,采用奇异值收缩算子法[20]解决:
Zk+1(t)=s(Xk+1(t)-Bk/β,λ2/β) ,
(19)
其中,s(H,τ)是在阈值τ处对矩阵H的奇异值进行软阈值操作的函数。
1.2 算法收敛性分析
对上述算法进行收敛性分析。由于算法中的每一时隙的数据重构主要进行ADMM迭代,因此,证明文中算法收敛只需证明ADMM在求解联合约束模型时是收敛的。
为了使证明表述更加简洁,首先定义了矩阵G和F:
G=Y(t)-Φv(X(t)) ,
(20)
(21)
然后,令矩阵H=[GT,FT,ZT],把式(10)重写为
(22)
其中,矩阵Q、P和W为
(23)
将式(22)写成增广拉格朗日函数的形式:
(24)
其中,J表示拉格朗日乘子,ϑ为罚参数。
文献[21]在Eckstein和Bertsekas定理的基础上给出了ADMM收敛的条件,即矩阵Q和P满足列满秩,f(·)为闭凸函数。其中式(24)中的矩阵Q和P满足列满秩,且函数f(H)是闭凸函数(其中1范数、2范数以及核范数都是凸函数)。因此,笔者提出的算法模型在ADMM算法下是收敛的。
2 仿真实验及性能分析
以两种真实数据集作为实验对象,对算法性能进行测试,每次试验得到的结果都是100次结果的平均值。实验前,对以上数据集均进行了预处理,将缺失、错误数据剔除,构造出完整的数据集。正则化参数λ1和λ2以及罚参数α和β需要预先设置。根据以往经验,不同的数据集的正则化参数不同,因此在实际实验中,根据输入数据集的特点,需要手动调整正则化参数的大小。其中正则化参数λ控制的是重叠区域误差约束正则项,λ控制的是低秩正则项。根据经验,将正则化参数λ的范围定为[0.001,0.010],λ的范围定为[0.000 1,0.00 1],将罚参数α的范围定为[0.000 5,0.005],β的范围定为[0.000 05,0.000 5],具体数值根据实验数据进行具体调整。
采用归一化的平均绝对误差(Normalized Mean Absolute Error,NMAE)来衡量算法的性能:
(25)
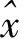
参与对比的算法包括:文献[22]中的克罗内克压缩感知方法(Kronecker Compressed Sensing,KCS),文献[12]中的正则化修正的压缩感知(Reg-mod-CS)方法,文献[19]中的序贯渐近压缩感知Seq-Prog-CS。实验中选择正交傅里叶矩阵作为的变换基Ψ。对于文中算法和Seq-Prog-CS算法,利用离散傅里叶变换和余弦变换构成Kronecker稀疏基,其他算法的参数设置同原文献。
实验1窗口大小的影响。
首先,检验窗口的大小对重构精度的影响。图4中给出了不同窗口长度对应的NMAE曲线。其中实验数据来自海洋监测数据集中的温度数据集和湿度数据集。待重构的时间序列的长度为128,窗口长度选取为4、8、16和32。从图中曲线的整体变化情况可以看出,随着观测数目的增加,整体的重构误差在逐渐减小;随着窗口长度的变长,重构误差逐渐减小,重构精度逐渐提高。这是因为窗口长度变长,使得更多的相关结构被纳入低秩矩阵中,使得低秩矩阵规模更大,计算更为准确。由于本实验仅为说明窗口大小对算法有一定的影响,且在该实验中5种传感器数据集的结果大同小异,限于文章篇幅,其他几种数据不再赘述。

(a) 温度数据集

(b) 湿度数据集
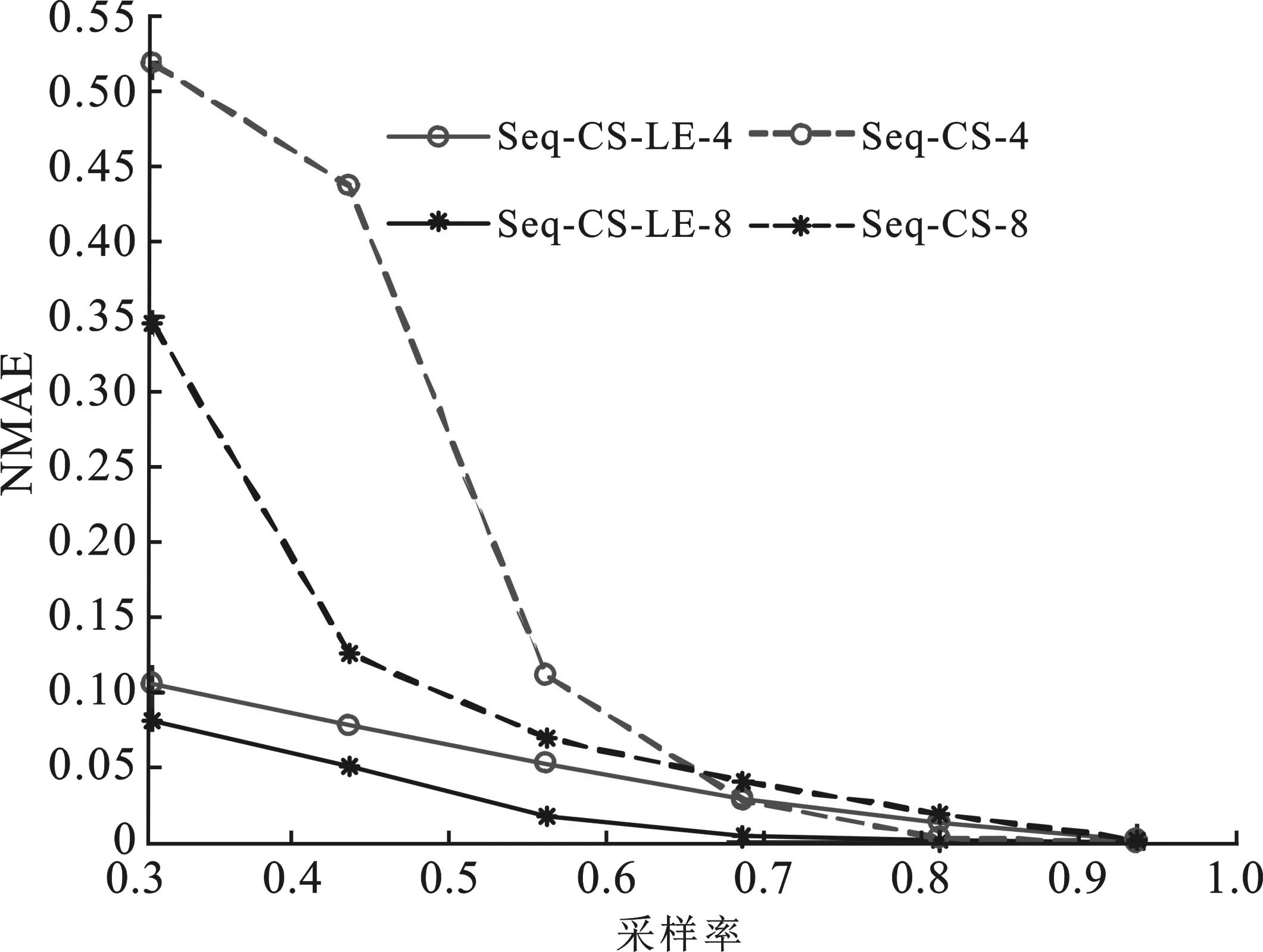
图5 低秩先验对重构性能的影响
实验2低秩先验对算法重构性能的影响。
笔者提出的算法将低秩先验加入到重构过程中,以提高重构精度。在实验中,为说明低秩先验的加入对重构性能的提高,以NCEP中的温度数据为例,将未加低秩先验的文中算法(Seq-CS)与文中算法(Seq-CS-LR)进行对比,图5中给出了两种窗口长度(w=4,w=8)的条件下,两种算法的重构性能对比。其中其他参数的设置从图5中的曲线可以看出,低秩先验的加入对重构性能有明显的提升,尤其是在采样率较低的条件下,能够大幅降低重构误差,提高重构精度。这是因为在序贯压缩感知推进重构时,形成的二维矩阵之间存在着时间相关和空间相关性,这一性质通过低秩性表现出来,将低秩先验加入到重构目标函数中,保证每次重构得到的数据矩阵满足低秩性。
实验3不同算法的重构性能对比。
将文中算法与其他算法进行重构性能对比。图6中分别给出了NCEP数据集中的湿度数据集和温度数据集下的重构性能曲线。其中对湿度数据集进行测试时,参数T=64,N=16,文中算法Seq-CS-LR与Seq-Prog-CS算法中的w=8;对温度数据集进行测试时,参数T=64,N=25,Seq-CS-LR与Seq-Prog-CS算法中的w=8。从图6中曲线可以看出,两种数据集下,文中提出的Seq-CS-LR算法的重构误差最小,从另外一个角度来看,几种算法达到同样的重构效果,Seq-CS-LR算法所需要的观测数目更少。具体来看,w=16时的Seq-CS-LR算法重构误差最小,w=8时的Seq-CS-LR算法的重构精度依然小于其他算法的。同时也验证了实验一种窗口的长度越长重构效果也好的结论,这是因为窗口越长,纳入低秩矩阵约束的列向量越多,获取的结构相关性越多,越有利于精确重构,因此在计算量可以接受的范围内,适当地延长滑动窗口的长度可以提高重构精度。
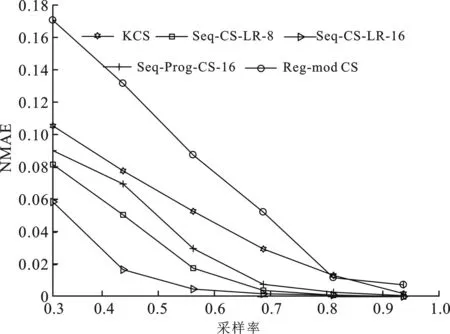
(a) 温度数据集

(b) 湿度数据集
3 结束语
笔者研究了海洋环境监测数据重构的问题,设计了一种多个传感器的时间流数据组成滑动矩阵的重构方法。该方法在DCS思想的影响下,根据滑动矩阵的低秩性引入合理的低秩正则化约束,同时利用前后时刻滑动矩阵的重叠区域数据相等的规律,加入了重叠区域误差校正项,有效提升了数据的重构质量。此外,在最优化目标函数求解过程中,利用成熟的ADMM技术,使得求解过程简单易操作。实验分析表明,低秩正则化能够有效提高重构精度,文中算法能够实现传感器网络数据的在线重构,在真实的海洋监测数据集下的重构性能皆优于其他几种传感器网络重构算法。由于笔者着重研究的是重构技术,直接采用的是已有性能较高的观测矩阵和时空相关稀疏基,弱化了稀疏基和观测矩阵的设计。
后续将对数据的在线采集进行深入研究,以进一步丰富序贯压缩感知理论。

