平面分割问题的探究之旅

广州大学数学与信息科学学院(510006);广州大学计算科技研究院(510006);广州市第二中学(510530) 程汉波

n条直线最多可将平面分割为多少个部分? 这个问题首先被瑞士几何学家斯坦纳提出并解决.很多著作在谈及“推理与证明”中“合情推理”与“演绎推理”应用时将其作为案例介绍,如波利亚的名著《数学与猜想: 数学中的归纳和类比》[1].大学组合数学教材在讲利用递推关系解决计数问题时也经常将其作为例题剖析,如曹汝成的《组合数学》(第二版)[2].人教版高中数学教材选修2-2 的教师用书在“自我检测题”部分也将其作为教学的补充资源供教师选用,而且,教材选修2-2 的复习参考题中有一道变式的习题:n个圆最多将平面分割为多少个部分? 当然,书中为突出合情推理中归纳推理的探究发现作用和演绎推理中数学归纳法的验证作用,以及整体难度的考虑,编写者将其设计成了问题串的形式引导师生探究.由此可见,这类分割问题备受青睐.

除了直线与圆分割平面问题,若考虑折(曲)线,则会出现更多更为丰富的平面分割问题.譬如,n条“X 形折线”(由两条相交直线组成)最多可将平面分为多少个部分呢? 如图1(a)(b),1 条“X 形折线”可将平面分为4 个部分,2 条“X 形折线”最多将平面分为11 个部分, …….不难发现,每条“X形折线”相当于两条相交直线”,于是n条“X 形折线”相当于2n条直线,若引用文[1]、[2]中的结果:n条直线最多可将平面分为个部分,则可知n条“X 形折线”最多可将平面分为a2n=2n2+n+1 个部分.

图1(a)

图1(b)

类似地,n条“V 形折线”(由有公共端点的两条射线组成)最多可将平面分为多少个部分呢?n条“W 形折线”(由两条线段与两条射线连接组成)最多可将平面分为多少个部分呢?n条“N 形折线”(由一条线段与两条射线(不一定平行)连接组成)最多可将平面分为多少个部分呢?n条“O 形曲线”(由一条封闭曲线组成)最多可将平面分为多少个部分呢? 不难发现,若以上问题得以解答,则n条“L 形折线”、“U形曲线”、“M 形折线”、“Z 形折线”、“S 形曲线”、“D 形曲线”最多可将平面分为多少个部分的问题也分别随之解决.本文给出这几类折线分割平面问题的探究思路与解答过程,读者可类似地探究更为丰富有趣的折(曲)线分割平面问题.

1.“V 形折线”平面分割问题

如图2(a)(b)所示, 1 条“V 形折线”将平面分为2 个部分;2 条“V 形折线”最多将平面分为7 个部分,即增加了5 个部分.具体而言,要使分割平面所得部分数保持最多,新添加的这条“V 形折线”的两边应与原来那条“V 形折线”的两边都相交,这就新交出了2×2=4 个新交点,这4 个点把新添加的这条“V 形折线”分为5 段,每一段将它穿过的那个区域(由原“V 形折线”分成的)一分为二,因此分割平面所得部分数增加了5 个部分.

图2(a)

图2(b)

一般地,假设n-1 条“V 形折线”最多将平面分为bn-1个部分,则n条“V 形折线”最多将平面分为bn个部分,即增加了bn-bn-1个部分.具体而言,要使分割平面所得部分数保持最多,新添加的第n条“V 形折线”的两边应与原来n-1条“V 形折线”的两边都相交,而且交点与原交点均不相同,这就新交出了4(n-1)个交点,这4(n-1)个点把新添加的这条“V 形折线”分为4n-3 段,每一段又将它穿过的那个区域(由前n-1 条“V 形折线”分成的)一分为二,因此分割平面所得部分数增加了4n-3 个.所以,bn-bn-1=4n-3.注意到b1=2,利用叠加法不难求得,bn=2n2-n+1.

当然地,以上思路也可以进行简化如下: 新添加第n条“V 形折线”进来后,新增加了4n-3 个区域,等于新增加的交点数4(n-1)与这条“V 形折线”条数1 的数值之和.因此,要计算n条“V 形折线”最多将平面分为多少个部分,只需在1 个部分(0 条“V 形折线”分平面所得部分数)的基础上加上总的“V 形折线”条数与交点数之和,而每两条“V 形折线”均有4 个交点,故总交点数为所以,n条“V 形折线”最多可将平面分为bn= 1+n+4C2n= 2n2-n+1 个部分.

其实,也可将“V 形折线”分平面问题转化为直线分平面问题.如图3,将1 条“V 形折线”在顶点处反向延长,会得到两条相交直线,分割平面所得部分数由2 增加至4.类似地,将n条“V 形折线”全部在顶点处反向延长,则可得到2n条相交直线,分割平面所得部分数会增加n个,所以,n条“V 形折线”最多分割平面所得部分数等于2n条直线最多分割平面所得部分数a2n再减去2n,即bn=a2n-2n=2n2-n+1,可谓殊途同归.

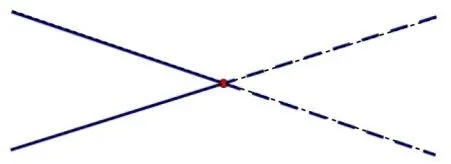
图3

2.“W 形折线”平面分割问题

如图4(a)(b)所示,1 条“W 形折线”将平面分为2 个部分;2 条“W 形折线”最多将平面分为19 个部分,即增加了17个部分.具体而言,要使分割平面所得部分数保持最多,新添加的这条“W 形折线”的四边应与原来那条“W 形折线”的四边都相交,这就新交出了16 个新交点,这16 个点把新添加的这条“W 形折线”分为17 段,每一段将它穿过的那个区域(由原“W 形折线”分成的)一分为二,因此分割平面所得部分数增加了17 个部分.

图4(a)

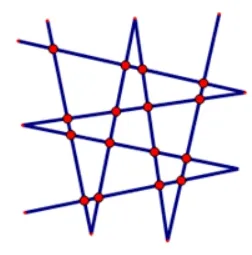
图4(b)

一般地,假设n-1 条“W 形折线”最多将平面分为cn-1个部分,则n条“W 形折线”最多将平面分为cn个部分,即增加了cn -cn-1个部分.具体而言,要使分割平面所得部分数保持最多,新添加的第n条“W 形折线”的四边应与原来n-1 条“W 形折线”的四边都相交, 而且交点与原交点均不相同,这就新交出了16(n-1)个交点,这16(n-1)个点把新添加的这条“W 形折线”分为16n-15 段,每一段又将它穿过的那个区域(由前n-1 条“W 形折线”分成的)一分为二,因此分割平面所得部分数增加了16n-15 个,所以,cn-cn-1=16n-15.注意到c1=2,利用叠加法不难求得,cn=8n2-7n+1.

当然地,以上思路也可以进行简化如下: 新添加第n条“W 形折线”进来后,新增加了16n-15 个区域,等于新增加的交点数16(n-1)与这条“W 形折线”条数1 的数值之和,因此,要计算条“W 形折线”最多将平面分为多少个部分,只需在1 个部分(0 条“W 形折线”分平面所得部分数)的基础上加上总的“W 形折线”条数与交点数之和,而每两条“W 形折线”均有16 个交点,故总交点数为,所以,n条“W 形折线”最多可将平面分为cn=1+n+=8n2-7n+1个部分.

其实, 也可将“W 形折线”分平面问题转化为“V 形折线”分平面问题.将图5(a)中“W 形折线”在每个顶点处反向延长, 会得到图5(b), 可将其看作图5(c)中两条“V 形折线”(分别用实线和虚线画出),分割平面所得部分数由2 增加至7.类似地,将n条“W 形折线”全部在每个顶点处反向延长,则可得到2n条“V 形折线”,分割平面所得部分数会增加5n个,所以,n条“W 形折线”最多分割平面所得部分数等于2n条“V 形折线”最多分割平面所得部分数bn减去5n,即cn=bn-5n=8n2-7n+1,也可谓殊途同归.

图5(a)

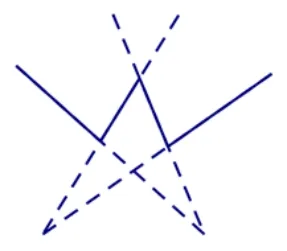
图5(b)

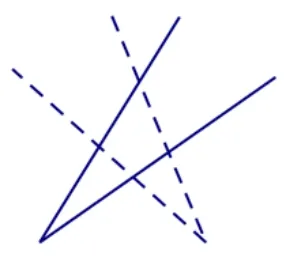
图5(c)

3.“N 形折线”平面分割问题

如图6(a)(b)所示, 1 条“N 形折线”将平面分为2 个部分;2 条“N 形折线”最多将平面分为12 个部分,即增加了10个部分.具体而言,要使分割平面所得部分数保持最多,新添加的这条“N 形折线”的三边应与原来那条“N 形折线”的三边都相交,这就新交出了9 个交点,这9 个点把新添加的这条“N 形折线”分为10 段,每一段将它穿过的那个区域(由原“N 形折线”分成的)一分为二,因此分割平面所得部分数增加了10 个部分.

图6(a)

图6(b)

一般地,假设n-1 条“N 形折线”最多将平面分为dn-1个部分,则n条“N 形折线”最多将平面分为dn个部分,即增加了dn -dn-1个部分.具体而言,要使分割平面所得部分数保持最多,新添加的第n条“N 形折线”的三边应与原来n-1 条“N 形折线”的三边都相交,而且交点与原交点均不相同,这就交出了9(n-1)个交点,这9(n-1)个点把新添加的这条“N 形折线”分为9n-8 段,每一段又将它穿过的那个区域(由前n-1 条“N 形折线”分成的)一分为二,因此分割平面所得部分数增加了9n-8 个,所以,dn-dn-1=9n-8.注意到d1=2,利用叠加法不难求得,

当然地,以上思路也可以进行简化如下: 新添加第n条“N 形折线”进来后,新增加了9n-8 个区域,等于新增加的交点数9(n-1)与这条“N 形折线”条数1 的数值之和,因此,要计算n条“N 形折线”最多将平面分为多少个部分,只需在1 个部分(0 条“N 形折线”分平面所得部分数)的基础上加上总的“N 形折线”条数与交点数之和,而每两条“N 形折线”均有9 个交点,故总交点数为9C2n,所以,n条“N 形折线”最多可将平面分为个部分.

其实,也可将“N 形折线”分平面问题转化为直线分平面问题.将图7(a)中“N 形折线”在每个顶点处反向延长,会得到图7(b)三条直线,分割平面所得部分数由2 增加至7.类似地,将n条“N 形折线”全部在顶点处反向延长,则可得到3n条直线,分割平面所得部分数会增加5n个,因此,n条“N 形折线”最多分割平面所得部分数等于3n条直线最多分割平面所得部分数an减去5n,即也可谓殊途同归.

图7(a)

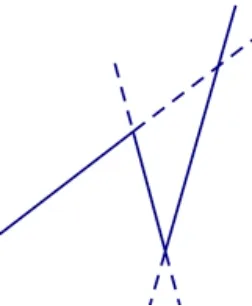
图7(b)

4.“O 型曲线”平面分割问题

如图8(a)(b)所示, 1 条“O 型曲线”将平面分为2 个部分;2 条“O 型曲线”最多将平面分为4 个部分,即增加了2 个部分.具体而言,要使分割平面所得部分数保持最多,新添加的这条“O 型曲线”应与原来那条“O 型曲线”相交,这就新交出了2 个交点,这2 个点把新添加的这条“O 型曲线”分为2段,每一段将它穿过的那个区域(由原“O 型曲线”分成的)一分为二,因此分割平面所得部分数增加了2 个部分.

图8(a)

图8(b)

一般地,假设n-1 条“O 型曲线”最多将平面分为fn-1个部分,则n条“O 型曲线”最多将平面分为fn个部分,即增加了fn -fn-1个部分.具体而言,要使分割平面所得部分数保持最多,新添加的第n条“O 型曲线”应与原来n-1 条“O 型曲线”都相交,而且交点与原交点均不相同,这就交出了2(n-1)个新点,这2(n-1)个点把新添加的这条“O 型曲线”分为2(n-1)段,每一段又将它穿过的那个区域(由前条“O 型曲线”分成的)一分为二,因此分割平面所得部分数增加了2(n-1)个部分,所以,fn-fn-1= 2(n-1).注意到f1=2,利用叠加法不难求得,fn=n2-n+2.

当然地,以上思路也可以进行简化如下: 新添加第n条“O 型曲线”进来后,新增加了2(n-1)个区域,等于新增加的交点数2(n-1),因此,要计算n条“O 型曲线”最多将平面分为多少个部分,只需在2 个部分(1 条“O 型曲线”分平面所得部分数)的基础上加上总的“O 型曲线”交点数之和,而每两条“O 型曲线”均有2 个交点,故总交点数为,所以,n条“O 型曲线”最多可将平面分为fn=1+=n2-n+2个部分.

其实,若联系拓扑学中著名的欧拉定理:V -E+F=2,V,E,F分别表示几何图形中的顶点数, 线条数和区域数,则该问题也可以解决得很巧妙.因为要使分割平面所得部分数保持最多, 则每两个圆之间都应有两个交点, 因此n条“O 型曲线”共有=n(n-1)个交点, 即图形的顶点数V=n(n-1); 又由于每条“O 型曲线”被分成2(n-1)段,故n条“O 型曲线”共被分成2n(n-1)段,即图形的线条数E= 2n(n-1).若设n条“O 型曲线”可将平面分为F个部分,由欧拉公式知,V+F -E= 2,所以,F=E-V+2=2n(n-1)-n(n-1)+2=n2-n+2,即n条“O 型曲线”最多可将平面分为n2-n+2 个部分,也可谓殊途同归.

综上观之, 平面分割问题灵活丰富有趣, 特殊化、一般化、类比和化归等数学思想方法在整个探究过程中熠熠生辉.正如波利亚把一般化、特殊化和类比并列地称为“获得发现的伟大源泉”.英国著名数学家梅森在集中研究了数学中的特殊化和一般化方法及其在解题中的作用后也认为: 特殊化与一般化正是数学思维的核心, 同时也是怎样解题的关键.匈牙利著名数学家路莎·彼得对数学家典型的思维和推理过程评论道: 数学家们往往不是对问题进行正面的攻击,而是不断地将它变形,直到把它转变成已经能够解决的问题.