基于马尔科夫模型的回归研究及其应用
何成刚,丁宏强,陈思宝,罗 斌,王家鑫
(1.安徽大学 计算机科学与技术学院,安徽 合肥 230031;2.安徽大学 计算智能与信号处理教育部重点实验室,安徽 合肥 230039 3.美国德州大学阿灵顿分校 计算机科学与工程系,美国 阿灵顿 TX76019)
0 引 言
回归分析的研究,一直是机器学习研究领域的热点,它能根据历史数据的特点,拟合出回归模型进行准确的预测,广泛应用在实际问题处理中。回归分析[1]的方法,就是对大量的数据进行相关的统计处理,通过寻求恰当的模型来探索出这些变量的内在关系,构造具体的回归模型,然后再根据相关的数据指标来对回归的效果进行评价。通过分析评价的结果得到较好的回归模型,从而运用回归模型来进一步有效的进行预测的研究与应用。神经网络理论、支持向量机(support vector machine,SVM)等这些人工智能(机器学习)的方法被用于回归分析之中,形成了一些回归方法,如SVM回归[2]、广义回归神经网络(generalized regression neural network,GRNN)[3],但是这些方法计算量太大,对计算模型和数据的准确性要求很高,局限性强。近些年来,随着马尔科夫理论的进一步发展,其在语音的识别[2]、金融序列分析[3]等方面取得了良好的效果。该文期望通过将马尔科夫理论与回归分析方法相结合,得到更好的基于马尔科夫理论的回归模型来进行回归预测工作的研究与应用。
主要贡献如下:
(1)将多元回归和Markov模型相结合,使用多元回归的方法解决Markov模型中转移矩阵难以确定的痛点,提出了基于多元回归的Markov回归模型,并将其应用到国民收入的预测之中,取得了很好的效果。
(2)将Regime Switching Model[4-5](体制转换模型)和Markov模型相结合,提出了马尔科夫转换(Markov-switch)回归模型,并将其应用于UCI数据集上和SVM回归算法进行比对,取得了非常好的效果。
(3)大胆提出将机器学习和经济学进行跨学科创新融合,利用跨学科知识互补的优势,使得回归模型的研究得到了进一步的发展和扩充。
1 机器学习方法的回归预测相关工作
对于回归问题的研究,国内外的科学工作者都进行了广泛的探讨。在传统的回归分析方法中,函数逼近理论分析思想严密,体系结构完整。但是由此发展而来的许多算法都有一些共同的缺点:计算量太大,对计算模型和数据的准确性要求很高,局限性强。然而把人工神经网络应用于函数逼近有着很多的优点,具体体现在数据的特征不是很明确,数据模糊或含较多噪声和非线性等情况[6-7]。
1.1 BP神经网络的回归预测
BP神经网络[3]是1986年由Rumelhart和McCelland领导的科学家小组在《并行分布式处理》一书中提出来的,本书中对具有非线性连续变换函数的多层感知器的误差反向传播算法进行了详尽的分析,实现了Minsky关于多层网络的设想[3-4]。BP神经网络的结构,反向传播(back propagation)神经网络,简称为BP神经网络。标准BP神经网络分3层,即输入层、隐含层和输出层,如图1所示。
在神经网络中误差反向传播网络和径向基函数(radial basis function,RBF)网络[8]是多层前向网络的两种典型网络,它们能够任意逼近任何非线性函数。由于它们结构简单、易于实现,已在时间序列分析、非线性函数回归估计中得到了广泛的应用。然而,由于网络结构难以确定、存在过学习、容易陷入局部极值等问题,限制了此种网络的发展。

图1 三层BP神经网络的结构
1.2 GRNN神经网络的回归预测
GRNN(广义回归神经网络)[3]最早是由Sprecht提出的一种基于非线性回归理论的前馈式神经网络模型。由于GRNN网络的训练速度快和非线性映射能力很强,可以将其运用于函数逼近。广义回归神经网络的思想是:用径向基函数作为隐含层中各个节点的基,构成隐含层空间。隐含层对输入向量进行变换,将低维空间的模式变换到高维空间内,使得在低维空间的模式变换到高维空间内,使得在低维空间内的线性不可分问题在高维空间内线性可分。利用径向基神经元和线性神经元建立了广义回归神经网络(GRNN),并将GRNN应用于了函数的逼近,取得较好的效果。GRNN网络的结构分析,利用径向基神经元和线性神经元可以创建广义回归神经网络。广义回归神经网络是由一个径向基网络层和一个线性网络层组成,见图2,其中ai1表示第一层输出a1的第i个元素,Wi1表示第一层权值矩阵w1的第i行元素。P表示输入向量,R表示网络输入的维数,S表示每层网络中的神经元个数,同时还表示训练样本的个数,b1为隐含层阈值,符号⊗表示‖dist‖输出与阈值b1的元素之间的乘积关系。隐含层的传递函数为径向基函数,广义回归神经网络连接权值的学习修正仍然使用BP 算法。广义回归神经网络中人为调节的参数少,只有一个阈值,网络的学习全部依赖数据样本,这个特点决定了网络得以最大限度地避免人为主观假定对预测结果的影响。

图2 广义回归神经网络的结构
但是,同样由于该网络结构难以确定、存在过学习、容易陷入局部极值等问题限制了此种网络的发展。上述三种网络都建立在渐进理论基础上,这三种网络需要无穷多的样本才能较真实地模拟样本的分布函数,而实际上所得的样本都是有限的。由此可以看出传统的神经网络在回归预测方面还是存在许多不可逆转的缺点,因此需要探索新的回归方法。
1.3 基于SVM的回归预测
Vapnik等人[6]为了解决神经网络在处理回归问题上的瓶颈,提出了统计学习理论,专门研究小样本情况下机器学习的规律,并给出了该框架下的一种具体实现─支持向量机[6]。支持向量机,形式类似多层前向网络,在学习机器的结构复杂性和学习精度之间寻求折衷,获得最优泛化能力。它着眼于现有的有限小样本,将求取模型最优超平面问题转化为二次规划问题,求得全局最优。同时,将非线性问题通过核映射将样本映射到高维特征空间,在特征空间求取最优超平面,避免了繁杂的内积计算。该算法的主要目的是利用核函数在具体的特征空间Ω下实现线性回归,具体的回归函数为f(x)=(ω,φ(x))+b,其中φ:Rd→Ω,(ω,φ(x))表示特征空间中的内积运算,ω∈Ω,b∈R, 通过极小化下面的目标函数:


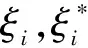
2 基于Markov回归模型的研究
该文将Markov 模型和回归相结合,提出了Markov多元回归模型,取得了良好的效果。同时将Markov和switch机制相结合,提出了马尔科夫转换(Markov-switch)回归模型,并将其应用于UCI公共数据集上,取得了良好的效果。
2.1 基于多元回归的Markov回归模型的研究与应用
在马尔科夫的预测问题研究[7]中,关键的地方是确定转移矩阵,但是由于具体问题的复杂性,往往使得转移矩阵难以确定。而回归分析[8-10]则是根据大量的观测数据值,建立相关的数学模型,设出相关的待估参数,然后再利用观测数据进行拟合,从而求出待估参数,得到具体的数学模型,最后对得到的模型进行评价。本部分利用多元回归理论进行数据的回归分析,求出马尔科夫模型的转移矩阵,从而建立起马尔科夫的回归模型。
2.1.1 多元回归模型
一般的形如
y=a0+a1x1+a2x2+…+an-1xn-1+anxn+ε
(1)
称为多元回归的线性模型[1]。其中,ε是误差,且要求ε独立同分布,a0,a1,…,an是未知量。公式(1)中只有一次观测误差ε,没有不同次观测值误差之间的关系,然而在实际的具体问题中,为了确定线性回归模型的未知参数,一定要有若干次的观测值序列,即:
所得到的多元回归方程为:
(2)
在实际的统计问题中,根据Gauss-Markov条件[11-12]通常把误差ε1,ε2,…,εn独立同分布的要求降低为E(εi)=0,D(εi)=σ2。同时可以将式(2)表示为下面的情况, 令:
则式(2)可以写为:
Y=Xα+ε
(3)
其中,E(ε)=0,D(ε)=σ2。
在具体的问题中,通过收集或者实验可以得到一定数量的观测值序列:
进而通过这些值来对式(2)中的参数a0,a1,…,an,σ2进行求值估计,通常采用最小二乘法[10],选择适当的α,使得残差平方和:

(y-Xα)'(y-Xα)
达到最小值。
2.1.2 马尔科夫回归模型

(4)
将式(4)具体写出,即为:
(5)
简写为Y=XA,其中aij,i,j=1,2,…,n为需要估计的参数,此时采用多元回归的方法来进行参数的估计,设在t时刻误差变量为εt(j),j=1,2,…,n,这时有:
2.1.3 马尔科夫回归模型的求解
根据多元回归的理论,可以用最小二乘法[13-15]来求解模型,令:
Yj=(y1(j),y2(j),…,yn(j))'
Aj=(a1j,a2j,…,anj)'
εj=(ε1(j),ε2(j),…,εn(j))'
从而式(5)可以写为:
Yj=XAj+εj,j=1,2,…,n
构造残差平方和可得:

(XX'Aj-X'Yj)'((X'X)(X'X)-1Aj-
X-1Yj)=
(XX'Aj-X'Yj)'(X'X)-1(XX'Aj-X'Yj)
2.1.4 基于多元回归的马尔科夫回归算法的设计
算法1:多元回归的马尔科夫回归算法。
输入:实验数据,并对数据进行处理。
(a)用最小二乘法来确定Markov转移矩阵;
(b)判断|XX′|是否为0,如果为则跳出本次程序,否则进行(c)步运算;
(c)根据Markov转移矩阵来确定不同参数的方程;
(d)根据已知的数据,由确定的方程来进行数据的拟合;
(e)计算误差(真实值-拟合值)。
输出:确定显著性评价水平,对回归方程进行假设检验(F检验)。
2.2 基于Markov-switch的回归研究
2.2.1 体制转换模型
Hamilton,Kim and Nelso等人在20世纪90年代提出了Regime Switching Model[16],并将其用于时间序列的分析之中。随着Markov理论的发展,经济学家们认识到在整个经济活动的过程中,通用的经济模型如差分自回归移动平均模型[12](autoregressive integrated moving average model,ARIMA),模型中的参数并不为常数,而是存在着具体的结构变化,必须将总体样本分解成若干个拥有不同参数的子样本,而且由于数据来自不同的产生过程,所以回归方程也会从一个状态向另一个状态转变。国外的许多学者对有关经济、金融时间序列的离散转换模型进行了许多的研究,得出允许序列变量非线性、动态地发生改变。最初的体制转换模型为:
yt=μi+εt
(6)

(7)
(8)
这样对于不同的状态,误差项对应于不同的状态中,同时也反映了不同的可信度标准,对用不同的自变量,所得的因变量序列也将是不同的。
2.2.2 Markov-switch转换回归模型
由此可以扩展,对于基于Markov理论的体制转换模型[17],状态的转换过程是随机的,一个确定的状态可能转换为其他的任意状态,也可能转换为自己的状态(即不发生状态的转换)。在整个状态的转换过程中,每个状态转换为其他的状态或是转换为自己的状态,可以用状态转移矩阵来进行控制。状态转移矩阵为:
其中,aij表示从i状态转换为j状态的概率。这样对于k个状态的Markov转换模型为:
2.2.3 马尔科夫转换回归模型的算法
输入:数据序列,从中提取因变量Y,和自变量序列(x1,x2,…,xn),状态转换个数K。
(a)计算在数据序列存在的情况下,状态序列的条件概率,即为:
P(Xt=xt,Xt-1=xt-1,…,X1=x1∣yt-1,yt-2,…,y1)=
P(Xt=xt∣Xt-1=xt-1,Xt-2=xt-2,…,X1=x1,yt-1,yt-2,…,y1)
P(Xt-1=xt-1,…,X1=x1∣yt-1,yt-2,…,y1)
其中,根据Hamilton[16]的体制转换模型,这里可以写为:
P(Xt=xt,Xt-1=xt-1)=
P(Xt=xt∣Xt-1=xt-1,Xt-2=xt-2,…,X1=x1,yt-1,yt-2,…,y1)
(b)计算联合条件概率密度分布(该算法的密度函数为正态分布):
f(yt,Xt=xt,Xt-1=xt-1,…,X1=x1∣yt-1,yt-2,…,y1)=
f(yt|Xt=xt,Xt-1=xt-1,…,X1=x1,yt-1,yt-2,…,y1)·P(Xt=xt,Xt-1=xt-1,…,X1=x1∣yt-1,yt-2,…,y1)
这里采用f~N(0,1)。
(c)计算数据序列的概率密度函数。
f(yt|yt-1,yt-2,…,y1)=

(d)通过Step4的计算可以得出:
P(Xt=xt,Xt-1=xt-1,…,X1=x1|yt-1,yt-2,…,y1)=
输出:通过上面的计算输出模型的标准差、相关系数和程序运行的时间。
3 实验结果及分析
实验1(基于Markov多元回归模型在国民收入的应用)。
实验使用广东省主要年份国民收入使用额统计数据(1952-1995)来进行回归实验,见表1[18]。
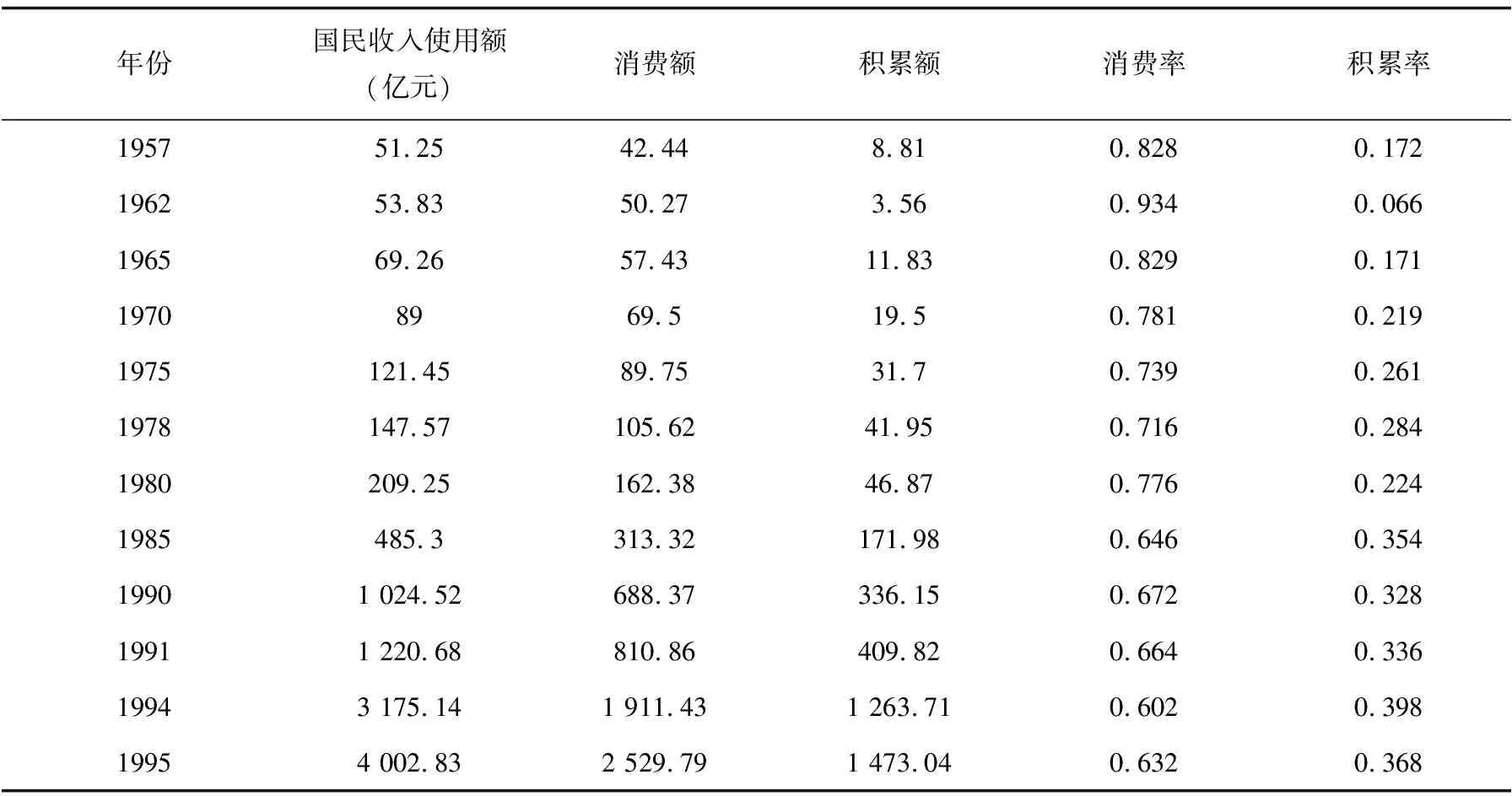
表1 广东省主要年份国民收入使用额统计数据(1952-1995)
采用消费率和积累率作为实验的数据,由算法1可以得到马尔科夫的转移矩阵为:

从而得到广东省主要年份的国民收入的消费率和积累率的回归方程为:

用回归方程进行数据的测算实验可以得到表2。
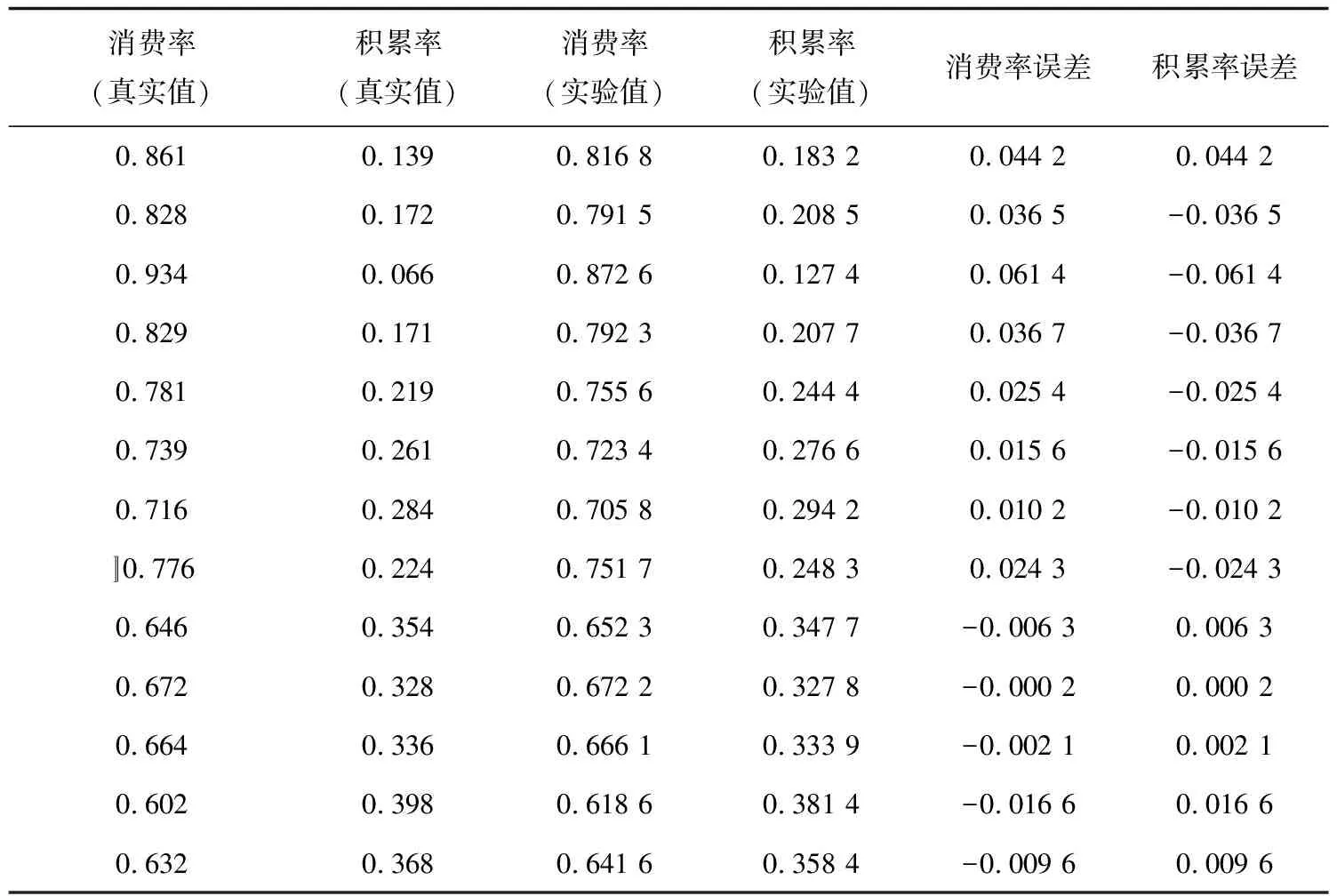
表2 消费率与积累率的真实值与实验值的比对
这里对上面的方程在显著性水平为0.05和0.025的情况下,进行假设检验可得:
F1(2,30)=6.589 2>F0.05(2,30)=3.32
F1(2,30)=6.589 2>F0.025(2,30)=4.18
F2(2,30)=15.41>F0.05(2,30)=3.32
F2(2,30)=15.41>F0.025(2,30)=4.18
由表2可以看出,实验的效果很好,误差很小。因此,应用Markov的回归方法可以有效预测国民收入分配的情况。
实验2(Markov-switch回归模型)。
本实验采用UCI数据集的abalone数据集,是由4 177*8的一个数据集(实例是4 177种,属性是8维数),wine数据集。采用的回归衡量标准(样本标准差,相关系数),其中样本标准差为:
相关系数为:

样本标准差是衡量一组数据分散的程度,标准差越高,说明实验数据越离散,差异越大,也就是实验越不精确。反之,标准差越低,则说明实验的数据越聚合,差异较小,实验越精确。相关系数反映的是变量之间的相关程度,R值越大,表明误差越小,变量之间的线性相关程度越高。相关系数越大,也说明样本点较大程度地聚集在函数的回归曲线上,相关系数越小,说明样本点分布在回归曲线上下越离散。由实验结果可以看出,提出的Markov转换回归算法在标准差方面比SVM方法[19-21]小,说明实验数据聚合度好、差异小、实验精度高。Markov转换回归算法相关系数比SVM大,说明误差比SVM算法小,变量之间的线性相关程度高。在运行时间上,Markov转换回归算法比SVM算法缩短了50%,取得了非常好的效果。
实验结果见表3。

表3 实验结果
4 结束语
首先介绍了回归分析和预测的基本知识,其次分析了传统的神经网络如BP神经网络和广义回归神经网络在回归预测方面的研究,讨论了传统神经网络在回归预测方面的不足。随后分析了基于统计学理论的SVM回归预测算法,得出了此方法的不足之处。然后提出基于多元回归的马尔科夫模型,对其在回归预测方面的研究进行了探讨,使用多元回归的方法可以解决马尔科夫矩阵难以确定的问题,提升了马尔科夫算法的预测效率。最后对基于马尔科夫理论的转换回归模型进行了研究,提出了马尔科夫转换算法并通过实验和SVM回归算法进行比较得到良好的结果。

