非均匀自散焦PT系统中的不对称亮孤子

杜智景, 史 凯, 刘东帅, 董亮伟

(陕西科技大学 文理学院, 陕西 西安 710021)

0 引言

近年来,具有宇称-时间(Parity-time)对称性的复外势调制非线性系统中的孤子动力学受到了广泛关注.当增益-损耗较弱时,系统线性谱为全实,当增益-损耗超过相变过渡点时,系统表现为复的本征谱[1-3].宇称-时间(PT)对称要求复势满足V(x)=V*(-x)这一条件,即其实部偶对称,虚部奇对称[1-3].

自PT势引入非线性光学以来,人们已对局域和周期性反对称增益-损耗PT系统中的孤子进行了深入研究,发现了基阶[3]、偶极[4]、多峰[5]和缺陷[6]等形式孤子.此外,纯非线性晶格[7]和线性与非线性混合晶格[8]中的孤子已被讨论.最近,线性和非线性PT对称外势中的冷原子矢量时空孤子[9]、二次非线性介质中的部分PT对称孤子[10]、非局域PT对称孤子[11]、分数衍射PT对称孤子[12]、Scarff 势中PT对称基态孤子[13]等也被报道.

非线性材料制备技术的最新进展[14-22]表明,除了折射率之外,非线性也可以根据需要进行调制[23].孤子可存在于非线性、线性与非线性组合势调制的非均匀自聚焦介质中[24,25].自散焦介质中也存在相关的局域非线性结构.数年前得出的一个结论,当非线性向介质边缘的增长率大于rD时(D表示维度),亮孤子有可能被捕获[26-29].

迄今,PT系统所支持的孤子的实部和虚部都为偶对称或奇对称[3-8].而文献[17,30]中不对称振幅的孤子是从对称孤子中通过对称破缺分歧出来的.此外,当增益-损耗系数较大时,已报道的PT对称系统将不可避免地发生对称破缺.不破缺的PT对称只发生在非均匀自散焦介质和局域反对称增益-损耗组合分布的系统中[27].

本文揭示了局域或周期性增益-损耗调制的非均匀自散焦介质可支持多个分支的、具有不对称实、虚部分量的、振幅却对称的亮孤子.发现了一些有趣现象,包括不同孤子分支之间的合并、不破缺的PT对称性、周期性增益-损耗分布下孤子分支合并对的变化等.

1 理论模型

光场在非线性介质中的传播由振幅为q的标量非线性薛定谔方程描述:

(1)

方程(1)中：x和z分别是归一化的横向坐标和纵向坐标,σ(x)是关于x的偶函数,为散焦的非线性调制,R(x)表示反对称增益-损耗分布,γ为增益-损耗强度.

存在局域亮孤子要求自散焦非线性足够快地增加到介质边缘[26-29].类似文献[26],本文设置σ(x)=βexp(αx2).与传统PT对称系统不同,方程(1)中没有偶对称的线性折射率调制.偶对称的折射率调制由振幅偶对称的孤子所导致的非线性赝势所提供.与均匀自散焦非线性相反,孤子的衰减尾部使其置于线性化系统的半无限带隙中.本文设置β=1和α=0.5.只要|q|2是对称的,R是反对称的,方程(1)就满足PT对称.

假定方程(1)所支持的孤子为平面波解形式:q(x,z)=w(x)exp(ibz),其中孤子稳态解w(x)=wr(x)+iwi(t),wr和wi分别是初始解的实部和虚部,b是传播常数.将上述表达式代入方程(1)可得到一个非线性常微分方程,该方程可以通过松弛迭代法、牛顿共轭梯度法等数值求解.

2 局域增益-损耗调制系统中的孤子

首先,讨论局域增益-损耗调制系统中孤子的性质.考虑奇对称增益-损耗分布R(x)=xexp(-αx2).为了理解增益-损耗调制部分对孤子动力学的影响,可固定传输常数b而改变增益-损耗强度系数γ.

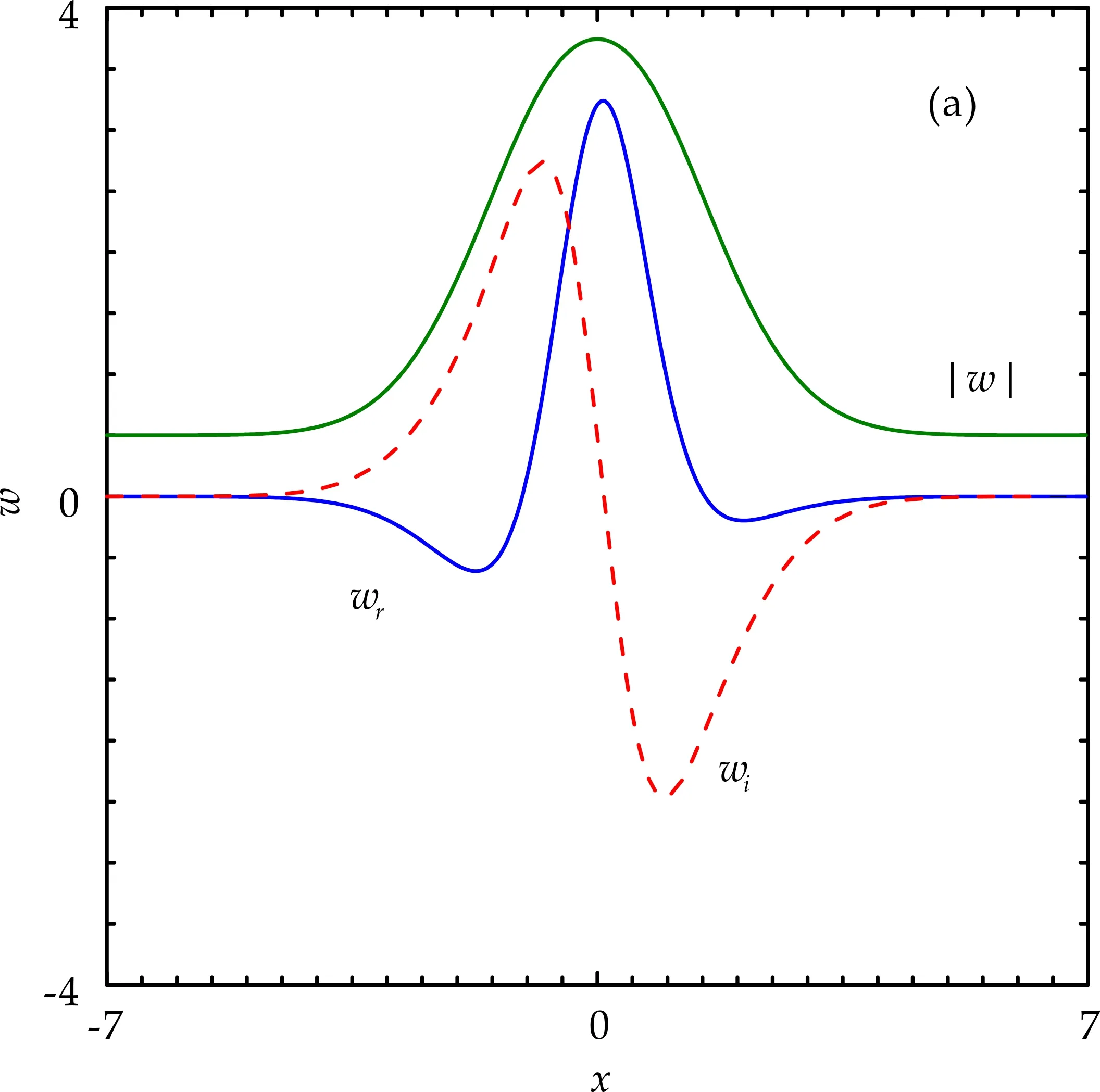
(a)γ=1.5，基阶孤子解

图1(f)给出了孤子在(b,γ)平面内的存在区域.γupp随着传播常数b的增加而非匀速减小,直到b=0时孤子消失.当γ≤γupp时传播常数b为纯实数.当γ>upp时,孤子不能存在.因此,现有系统中的孤子呈现出不破缺的PT对称性.

孤子的稳定性是一个非常重要的问题,可用线性稳定性方法加以分析.假定孤子微扰解形式为:

q=[wr+iwi+uexp(σz)+ivexp(δz)]exp(ibz)

这里u和v是振幅任意小的微扰,在传播时以复指数δ增长,δ为孤子的线性不稳定增长率.将微扰解q代入方程(1),围绕稳态解wr,i线性化方程(1)将得到一个本征值问题:

(2)

(a)γ=1.5，偶极孤子解

基于方程(2)的线性稳定性分析,发现基阶孤子和偶极孤子是完全稳定的(如图1(e)所示).如果γ低于临界值,三极孤子能够稳定传播.而当γ较大或者γ位于狭窄的不稳定窗口(点线)时,四极孤子是不稳定的.

与文献[17,30]中所述的不对称孤子相比,强调三点:首先,这里的孤子实部、虚部是不对称的,但其振幅是偶对称的;其次,γ的增长不会导致系统的对称破缺;第三,由于σ(x)的几何分布,孤子的存在区域和相应的线性谱之间没有直接联系.

3 周期性增益-损耗系统中的孤子

接下来,考虑周期性增益-损耗系统中的孤子.简单起见,设R(x)=sin(Ωx).尽管对应线性系统的带隙是完全封闭的,但孤子仍然可以存在.其物理原因在于非均匀介质使系统非线性化.非均匀非线性系统与其对应的线性化方程的频谱之间没有直接关系.对比图1和图2可发现,对于Ω=4,x轴上的R虚部节点数导致孤子的虚部节点数大于在局域增益-损耗系统中孤子的虚部节点数.实部和虚部的不对称性仍然可出现在孤子的各个分支.基阶孤子和偶极孤子在γupp=5.863处合并,三极孤子和四极孤子的合并点为4.134.这表明不同分支孤子之间的合并仅由非均匀散焦非线性决定.

与图1(e)所示孤子不同,基阶、偶极孤子的存在区间比三极、四极孤子宽(如图2(c)所示).在图2(c)中，f、d、t、q、five、six分别表示基阶、偶极、三极、四极、五极和六极孤子.同时,图2(c)中所有孤子分支的存在区间比图1(e)中宽.然而,周期性增益-损耗系统中孤子的稳定区域收缩.典型的不稳定性分析结果展示在图2(d)中.当γ超过临界值时,孤子是线性不稳定的.

(a)前五分支孤子的U-γ 曲线(实线:稳定;虚线:不稳定)

当周期性增益-损耗的空间频率增加时,仍然能够发现不对称孤子(如图3所示).有趣的是,孤子分支合并对发生了变化(如图3(a)所示).Ω=6时,基阶孤子不与任何其他孤子分支合并.偶极孤子和三极孤子在γupp=7.272合并,四极孤子和五极孤子之间的合并点是8.428.孤子的存在域随着Ω的增长而变宽.如果γ低于某一特定值,孤子的前四个分支是稳定的,而第五个分支则是完全不稳定的.

4 孤子传播仿真模拟

最后,应用分步傅里叶方法系统对于上述不同非线性调制作用下的多分支孤子做了传播仿真模拟.初始输入光场为q(z=0)=w(1+ρ) ,其中ρ为一个振幅较小的随机噪声.图4展示了两个代表性例子.直接数值传播模拟和稳定性分析结果完全符合.

在当前模型中也可以找到具有奇对称或偶对称分量的PT对称孤子.事实上,这种非线性激发孤子已经在文献[27,31]中报道.比较两种对称性不同的孤子,发现除了内部对称性外,不对称孤子的其他性质,包括功率、功率流密度、存在范围、稳定区间、不同孤子分支之间的合并等,都与对称孤子相同.这两类孤子可以看作是由同一个非线性系统支持的不同对称性的多稳态.这种现象在非线性导致的PT对称系统中应该是普遍存在的.

(a)γ=1.5,偶极孤子稳定传播模拟

5 结论

本文研究了局域或周期性奇对称增益-损耗和局域偶对称非线性折射率调制PT对称系统中的实、虚部不对称孤子的传播特性,发现了不对称多分支孤子之间的合并和不破缺的PT对称性.直接传播模拟和线性稳定性分析结果表明,不对称孤子要么是稳定的,要么是弱振荡不稳定的.本文的结论可推广到其它形式非均匀非线性赝势诱导的PT对称系统中.