构建对话课堂 助力“减负提质”
陈云


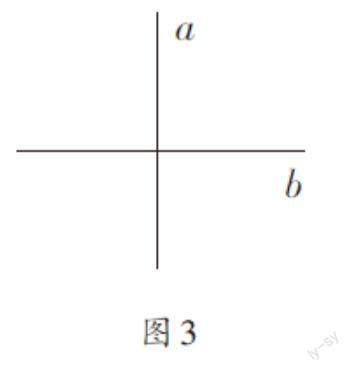
[摘 要]为了让“双减”政策落地,真正减轻义务教育阶段学生的作业负担和校外培训的负担,教师必须在课堂上下功夫,确保学生在课堂上学足、学好。“走向对话”的数学课堂,旨在课堂上采用多种手段,带领学生展开自然、深入的探究性学习。以“认识垂线”教学为例,概念教学就变得有温度、有深度、有力度、有广度、有高度。
[关键词]认识垂线;多元对话;概念学习
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2022)32-0073-03
随着新一轮课改的深入推进和“双减”政策的落地,我们坚持课堂教学的不断革新、优化,努力构建“走向对话”的“明道课堂”,以确保学生在课内能学足、学好。下面将结合“认识垂线”一课谈谈如何借“对话”帮助学生理解概念、运用概念,进而促进学生深度学习。
一、激趣式对话——让概念教学更有温度
德国著名的民主教育家第斯多惠说:“教育的艺术不在于传授本领,而在于激励、唤醒和鼓舞。”让“学”成为一种主动的、独立的、自觉的行为,俨然变成了这句话的重要内涵。采用对话的形式使一个好的情境成为学生思维的触发器、主动学习的催化剂,就能不断激发学生的学习兴趣,使概念教学充满趣味与活力。
在教学“认识垂线”时,笔者就巧借“帮助小兔家设计道路”将各知识点串联起来。
【教学片段1】
师(播放 “幸福村”的图像和音频):孩子们,幸福村为方便大家出行,准备经过小兔家修建一条公路穿过这条幸福大道,该怎么设计呢? 如果把小兔家看作一个点,把幸福大道看作一条直线,请你们做个小小设计师,帮助小兔家设计出这条公路。
展示学生作品:
师:这三种方案有什么相同的地方?
生1:这三种方案都是从小兔家出发引出一条直线。
生2:每种方案中的兩条直线都交到了一点。
生3:每种方案中的两条直线都形成了角。
师:又有什么不同呢?
生4:方案一和方案二的线是斜的,方案三的线是直的。
师:斜的、直的?谁能描述得更清楚?
生5:直的是说两条直线相交时出现了直角。
师:哪里有直角?可以怎么验证呢?
(学生采用多种方法验证,“两条直线互相垂直”的情况呼之即出)
师:哪种方案是从小兔家到幸福大道最短的路?说出你的理由。
生6:第三种方案。我是用眼睛看出来的。
师:好厉害!但数学是一门严谨的学科,不能光用眼睛看,还得验证。
生7:可以用直尺测量。
生8:测量容易出现误差,我们可以用一根线来逐一比较。
师:这条路与幸福大道有什么关系呢?
师(课件出示场景):小马家、小牛家、小狗家都在小兔家的旁边,它们到幸福大道的距离与小兔家到幸福大道的距离都相等,你能找到小马家、小牛家、小狗家的位置吗?如果也把它们的家看作点,把这些点连成一条直线,在这直线上的所有点到幸福大道的距离都相等,那这条直线和幸福大道所在的直线垂直吗?那它们又是什么关系呢?
就这样,借助“帮小兔家设计道路”的情境将“认识垂线”中的概念融合在一起,以核心问题作为导向、以平等交流作为手段、以智慧生成作为目的,不断地激发学生求知的欲望,学生在不知不觉中获得新知与知识背后的数学思想方法。
二、质疑式对话——让概念教学更有深度
《汉书·陈遵传》中有云:“时时好事者从之质疑问事。”疑不仅是思维的火花,更是开启学生思维的钥匙。质疑式对话就是“以学生为主体,以对话为主线,以质疑为特征”开展的有效对话。教学概念时,教师要引导学生在对话中质疑,在质疑中释疑,借助释疑完成知识的构建、思维的提升。
【教学片段2】
师:好好想想,两条直线互相垂直要有什么条件?如果旋转两条直线,现在这两条直线还互相垂直吗?为什么?再旋转,还互相垂直吗?
生1:不管两条直线的位置怎样,只要两条直线能够相交形成直角,它们就互相垂直。
师(出示图3):如果把其中一条直线表示为a,另一条直线表示为b,你准备怎样描述这两条直线的位置关系呢?(学生回答略)
这一环节的探究过程非常自然,感性与理性并重。教师在对学情精准把握以及对数学教材深度挖掘的基础上提出了直指“垂直”这一概念本质特征的问题,借师生、生生对话,巧妙地制造“事端”,让学生在追问、质疑与反省中获得对概念本质的深刻理解,形成数学核心素养。
三、聚焦式对话——让概念教学更有力度
日本东京大学教授佐藤学认为:学习是相遇与对话,是与客观世界对话、与他人对话、与自我对话的三位一体的活动。这种对话分享既可以表现为教师、学生和文本之间的对话,也可以表现为生生之间、师生之间的对话。生生之间的对话使得概念的内涵得以丰实,有利于拓展知识的宽度;师生之间的对话,更多的应该是提炼和提升,使意义得以穿越。
【教学片段3】
师(出示图4):图中的哪些直线是互相垂直的?
生1:只有第②组的两条直线是互相垂直的。
生2:第④组的两条直线也是互相垂直的。
师:依据是什么?
生2:我们可以用直角三角尺或量角器进行测量,不难发现它们相交成直角。
师:说得真好。还有互相垂直的两条直线吗?
生3:第⑤组的两条直线好像也是互相垂直。
生4:互相垂直的两条直线必须是相交的,可第⑤组的两条直线不相交。
生5:这两条直线相交了。
师:说出你的理由。
生5:因为直线是能够延长的。我们只要将两条直线延长一下,它们就相交了。
师:试着延长一下……果然相交了!它们相交了就说明它们垂直了吗?
生6:延长后,我们再用直角三角尺或量角器来进行测量,可以看出它们相交成了直角。
师:那第⑥组的两条直线互相垂直吗?
生7:第⑥组的两条直线不互相垂直。将这两条直线延长后,它们不能相交成直角。
师:通过刚才的练习,你有什么收获呢?(学生回答略)
孩子们说得多好呀!一语道出了“垂线”这一概念的本质。在此环节中,聚焦式对话实现了师生间、生生间良好的沟通。“垂线”这一概念的教学不是简单地告诉,而是动态地生成。课堂中生生之间的多向交流,让知识激活着知识,生命激扬着生命,心灵激荡着心灵。
四、开放式对话——让概念教學更有广度
“数学教学不应求全,而应求联。”数学知识之间是相互联系的,具有很强的系统性。鉴于此,教师要着眼数学知识的整体性,在沟通知识之间的纵横联系上做文章,借对话帮助学生把碎片化的知识点连成线、织成网,整合成完整的知识体系,在引导学生在理解的基础上,努力做到瞻前顾后、有的放矢。
【教学片段4】
师:动手操作,在正方形纸上画出两条相互垂直的直线,并做上标记。
生1:我是先把这张正方形纸横着对折一次,再竖着对折一次,此时这两条折痕是互相垂直的。
生2:我是把正方形纸沿着两条对角线进行对折,得到的这两条折痕也是互相垂直的。
师:不管我们是先横着对折再竖着对折,还是沿着两条对角线来对折,得到的两条折痕都是互相垂直的,此时的这个垂足就在正方形的中心。请测量一下正方形的中心到正方形各个顶点的距离。
生3:都相等。
师:刚刚测量的其实是我们之前学习的点到点之间的长度,也就是两点之间的距离。那正方形的中心到正方形各边的距离都相等?此时又测量什么呢?
生4:正方形的中心到正方形各边的距离也相等。
生5:此时测量的是点到直线的距离。
师:以后我们还会学习线与线之间的距离。
教师巧妙地借助动手操作、师生对话巩固了本课的“点到直线的距离”,复习了之前的“点到点之间的距离”,借一句“学习线与线之间的距离”又巧妙地将知识延伸到课外,既激发了学生对概念学习的浓厚兴趣,引领他们继续探究新知,又给予学生思考的路径,让学生获得的不仅仅是对概念的浅表认识,还有对概念的深刻理解,帮助学生学会学习,让课堂成为师生知识共建、情感共振、生命共长的地方。
五、反省式——让概念学习更有厚度
数学课程标准在基础理念中明确指出:应建立目标多元、方法多样的评价体系。评价应关注学生学习的结果,更应关注学习的过程,关注学生在数学活动中所表现出来的情感、态度、价值观,帮助他们认识自我、建立信心。因此,在数学课堂教学中,教师要设计关键性问题,有意识地引导学生将“回顾与反思”作为一个重要的学习过程,引导学生反思思考过程、反思探究过程、反思概念获得的全过程,进而提高元认知能力,以实现自我的超越。
【教学片段5】
师:请给自己本节课的表现打分。
生1:我给自己打95分。我对自己本节课的学习状况比较满意,对“垂线”意义的理解还可以,今天的练习我全对,但回答问题的次数较少。
师:老师对你今天的表现非常满意。老师关注到你课上举手非常积极,但由于回答问题的机会有限,所以你没能回答很多问题。
生2:我给自己打88分,今天在判断两条直线是否垂直时,我判断错了,没考虑到直线可以无限延长。
师:错误并不可怕,关键是你有没有真正理解,相信通过这道题,你会对概念的理解更深刻,今后对问题的思考会更全面。
……
学生的学习离不开反思,一方面,学生的学习是螺旋式上升的,学生对新知识的认知是在对已经掌握的知识进行反思的基础上实现的;另一方面,学生形成某些不正确的观念之后很容易根深蒂固,他们只有不断地深刻反省,才能真正地纠正。学会对学习活动进行真正地自我反省和调节,是学生个体智慧形成的标志。因此,概念教学时,教师要有目的地引导学生展开自我评价,进行自我对话,让学生主动地对学习过程、学习方法和经验等进行回顾与反思。唯有这样,学生才能获得真正意义上的“学有所悟”。
教之道在于“度”,学之道在于“悟”。一个“度”字包含了概念教学时,教师要善于运用各种方式让学生经历概念形成的过程,促使学生生成智慧、建构素养。一个“悟”字包含了学生在学习时的自我建构、自我理解、自我反省。
【本文系2020年度江苏省教育科学规划课题“‘教为不教教学观下小学数学深度学习的实践研究”(编号:YZ—c/2020/21)的研究成果。】
(责编 金 铃)

