关于一些图运算的逆和反度指标∗

张旻劭，马小玲

(新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830017)

0 引言

本文考虑的图均为简单连通图.设图G=(V(G),E(G)),其中V(G) 是G 的顶点集,E(G) 是G 的边集.我们用n=|V(G)| 和m=|E(G)| 分别表示图G 的顶点数和边数.dG(u) 表示点u 在图G 中的度数.设Δ(G) 和δ(G)分别为图G 的最大度和最小度.对于其他未定义的术语和概念,读者们可参阅文献[1].

拓扑指标是分子结构的数学描述符,被用来反映分子的大小,形状等结构特征,以此实现分子结构信息的数值化.由于分子拓扑指标计算简便,取值客观且不受实验的限制,因此应用非常广泛,现已有200 多种不同类型的拓扑指标被提出.常见的拓扑指标有Wiener指标,Randi´c指标,Zagreb指标,Hosoya指标等,可参阅文献[2-3].2010 年,Vukicevic和Gasperov[4]引入一个基于顶点度的图G的拓扑指标,即:逆和反度指标ISI(G),定义为其中du为图G 中点u 的度.在2017 年,Falahati-Nezhad[5]等学者用悬挂点的个数,最大度和最小度,半径等结构参数得到了ISI 指标的一些上下界.更多的有关ISI 指标的上下界的研究,我们可以参阅文献[6-9].近年来,一些学者研究了图运算,常见的图运算有笛卡儿积运算,冠运算,对称差运算等.关于图运算的研究,我们可以参阅文献[10-13].

1 准备工作

在这部分,我们首先给出一些拓扑指标和图运算的定义,这些内容将在我们后续的研究中起到重要的作用.1972年Gutman和Trinajstic[14]提出了第一Zageb指标和第二Zageb指标,分别定义为M1有关Zageb指标的历史背景和性质,我们可以参阅文献[15-16].

设图G1=(V(G1),E(G1)),G2=(V(G2),E(G2)),其中{u1,u2,···,un1}∈V(G1),{v1,v2,···,vn2}∈V(G2),图G1,G2的边数分别为|E(G1)|=m1,|E(G2)|=m2.

图连接运算,记为:G1∨G2,图G1和G2的图连接运算就是将G1中的每个顶点都连接到G2的每个顶点,同时保持G1和G2的原有边.G1∨G2的顶点集为V(G1∨G2)=V(G1)∪V(G2),边集为E(G1∨G2)=E(G1)∪E(G2)∪{uv|u ∈V(G1),v ∈V(G2)}.

笛卡儿积运算记为:G1×G2.G1×G2的顶点集为V(G1×G2)=V(G1)×V(G2),边集为E(G1×G2)={(u1,v1)(u2,v2)|u1=u2且v1v2∈E(G2),或者v1=v2且u1u2∈E(G1)}[17].

冠运算记为:G1°G2,是由一个G1和n1个G2的拷贝得到,并且G1的第i个顶点和G2的第i 个拷贝的所有顶点相连接而得到的图[8].

字典序积记为:G1[G2].G1[G2]的顶点集为V(G1[G2])=V(G1)×V(G2),边集为E(G1[G2])={(u1,v1)(u2,v2)|u1u2∈E(G1),或者u1=u2且v1v2∈E(G2)}[18].

对称差记为:G1⊕G2.G1⊕G2的顶点集为V(G1⊕G2)=V(G1)×V(G2),边集为E(G1⊕G2)={(u1,v1)(u2,v2)|u1u2∈E(G1) 或者v1v2∈E(G2),但两者不能同时存在}[19].显然,

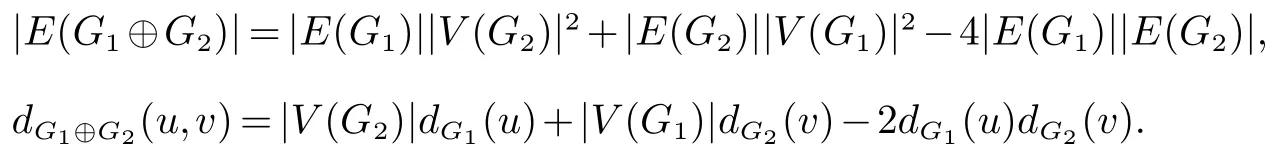
2 结论

接下来,我们将给出运算图的逆和反度指标的上界.

定理1设Gi是有ni个点,mi条边的简单连通图,其最大度是Δi,最小度是δi(i=1,2).那么

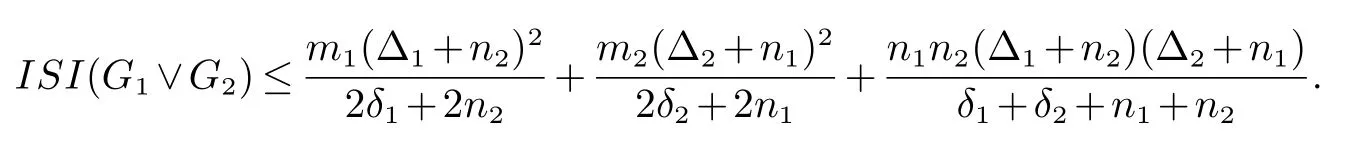
等号成立当且仅当G1和G2都是正则图.

证明设V(G1)={u1,u2,···,un1},V(G2)={v1,v2,···,vn2}.由图连接运算定义,如果u 是G1∨G2的一个点,那么

定理2设Gi是有ni个点,mi条边的简单连通图,其最大度和最小度分别为Δi,δi其中i=1,2.那么

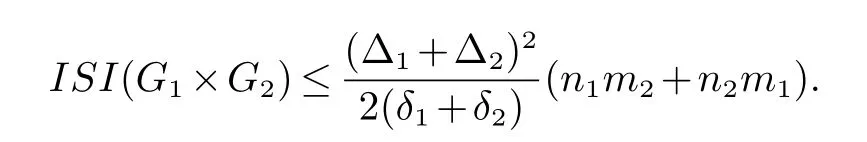
等号成立当且仅当G1和G2都是正则图.

证明设V(G1)={u1,u2,···,un1},V(G2)={v1,v2,···,vn2}.根据两个图的笛卡儿积运算的定义,可以得到经过图运算后图中每个点的度,即:

定理3设G1=(V(G1),E(G1)),G2=(V(G1),E(G2))为简单图,其中对于i=1,2,有|V(Gi)|=ni,|E(Gi)|=mi,其最大度和最小度分别为Δi,δi.那么

等号成立当且仅当G1和G2都是正则图.

证明根据两个图的冠运算的定义,设其边集可分为三部分,即:E(G1°G2)=E1∪E2∪E3,其中

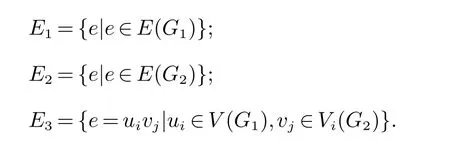
对于点u ∈V(G1°G2),点u 的度为

因此可以得到

定理4对于i=1,2,设Gi=(V(Gi),E(Gi))为简单图,其中|V(Gi)|=ni,|E(Gi)|=mi,他们的最大度是Δi,最小度是δi.则有

等号成立当且仅当G1和G2都是正则图.

证明设G1的顶点集为V的顶点集根据两个图字典序积的定义,可知经过图运算后得到的图中每个点的度,即

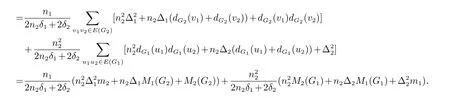
等式成立当且仅当dG1(u1)=dG1(u2)=Δ1=δ1,dG2(v1)=dG2(v2)=Δ2=δ2,对于ui∈V(G1) 并且vi∈V(G2).因此,图G1和图G2都是正则图.

定理5设Gi=(V(Gi),E(Gi))为简单图,对于i=1,2.设|V(Gi)|=ni,|E(Gi)|=mi,其最大度为Δi,最小度为δi.那么

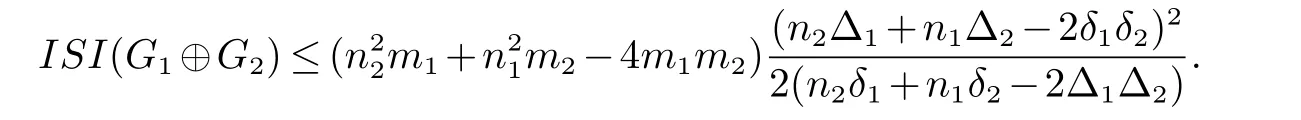
等号成立当且仅当G1和G2都是正则图.