二维狄拉克费米子及其拓扑态
邢燕霞,梁钰林
(北京理工大学 物理学院,北京 100081)
0 引言
拓扑相变是超越朗道相变的一种新的物态。朗道相变是对称破缺引起的相变,核心在于对称破缺[1-2]。在朗道相变的理论框架下,只要对称性相同,物质状态便相同。但是事实并非总是如此!在很多情况下,即便对称性相同,物质仍然可以有不同的相,这种相变被称作拓扑相变[3]。拓扑相变的本质是相互作用构架的改变,包括能级构架,量子纠缠的形态,等等。拓扑相变非常普遍,不管体系有多体相互作用体系,比如分数量子霍尔效应[4]、奇数自旋态[5],还是没有多体相互作用体系,比如整数量子霍尔效应[6]、拓扑绝缘体[7-11],都可能发生拓扑相变。不管发生在哪种体系,所有的拓扑态都展现了拓扑全息原理[12],一句话概括,边界决定体系拓扑态。边界可以形象地理解为地表地形地貌,这也是英文topology的本意。
拓扑相变产生的拓扑非平庸态分为两大类,一类是对称性保护的拓扑非平庸态,拓扑绝缘体的边缘态属于此类;另一类拓扑态则不必考虑对称保护,典型例子是整数量子霍尔态,又被称作陈拓扑绝缘体。这种拓扑态在任何情况下都具有鲁棒性,不像第一类拓扑态,必须在对称性保护下才具有鲁棒性。拓扑相变有两层含义:第一层,连续形变下的不变性;第二层,拓扑结构改变引起的性质跃变。要想表征这种拓扑物性,必须找一个物理量,能够全面体现以上两层含义,这个量我们称之为拓扑不变量[13-14]。拓扑不变量具有如下性质:第一,能区分拓扑平庸和非平庸,这是0和1的差别;第二,在连续形变作用下,值不变,0永远是0,1永远是1。无需对称性保护的陈绝缘体,其拓扑不变量是陈数[15],陈数源于量子力学的几何相(贝利相)[16]。需要对称性保护的拓扑绝缘体,通常使用Z2拓扑不变量[17],用缠绕数的奇偶性表征拓扑性[18-19]。本文不涉及Z2拓扑不变量,只关注由贝利相定义的拓扑陈数。对于某些特殊的拓扑绝缘体,比如时间反演对称保护的拓扑绝缘体,如果互为时间反演对称的两部分可以互相解耦,那么每一部分都相当于一个独立的陈绝缘体,这样的拓扑绝缘体也可以用拓扑陈数来表征其拓扑性。事实上,对称性保护下的两个手性相反的拓扑态总是成对出现,且在倒空间彼此相距较远,一般都处于相互解耦状态,可分别用拓扑陈数单独表征这两个手性相反的拓扑态。比如,石墨烯中互为时间反演对称的K能谷和K’能谷、外尔半金属中空间反演对称的一对外尔点,都可以作为独立的拓扑态,用贝利相定义的拓扑陈数表征其拓扑性。
贝利相就是贝利曲率的通量。一般来讲,判断体系的拓扑性,最直接的方法就是计算拓扑不变量,根据拓扑不变量对体系拓扑性进行分类。但是对于二能级系统,无需计算贝利曲率和贝利相,直接根据系统哈密顿量结构便可判断体系拓扑性。二能级系统之所以这么神奇,是因为所有的二能级系统都可以表示为二维狄拉克方程。通过参数映射,二维狄拉克方程可以连续形变成为理想的各向同性的二能级模型。各向同性的二能级模型可看做倒空间的单极点,贝利曲率等效于实空间的点电荷产生的电场,根据高斯定理,不管封闭曲面如何形变,其通量都不会变,所有可能的通量分为两类:第一类,封闭曲面包含奇点,角通量等于4π立体角,拓扑非平庸,拓扑陈数=1;第二类,封闭曲面不包含奇点,角通量为零,拓扑平庸,拓扑陈数=0。所有的二能级模型,根据映射后参数空间的拓扑结构,可直接判断体系的拓扑性。二能级模型虽然简单,但是它所包含的深刻物理,几乎可以用于所有凝聚态新材料的理论分析。
本文内容安排如下:第1节,系统阐述拓扑陈数的背景和物理含义,并说明在凝聚态能带理论框架下,如何运用拓扑陈数分析系统的拓扑性质;进一步分析贝利曲率的单极点,在不计算贝利曲率贝利相的前提下,直接根据参数结构,定性判断二能级体系的拓扑性;最后,聚焦二维狄拉克方程所描述的二能级系统,通过参数映射,再结合单极点模型,直接利用狄拉克方程的质量项,判断体系的拓扑性。第2、3、4节,分别以石墨烯、拓扑绝缘体、外尔半金属为例,展示并验证此方法。
1 贝利相和拓扑性
1.1 布洛赫波函数


考虑V(r)=0的极简模型。如果不考虑元胞内的势场分布,参数k空间的晶体哈密顿量将不显含动量算符p,算符型哈密顿量H(k)退化为参数型哈密顿量h(k)。这种情况下,只考虑元胞内部结构(比如复式晶格的子晶格,或者晶格内原子轨道之间的耦合,等等),相应的布洛赫能带将会非常简单。
1.2 贝利相
如果哈密顿量显含某参数R,理论上可以假设参数随时间缓慢变化,则体系满足含时薛定谔方程

绝热近似下,可引入正交归一的,满足瞬时定态薛定谔方程的基组

称为贝利连接,可类比磁矢势。至此,参数R(t)随时间变化的时间变量作为辅助变量,现已完全消失。以下只需关注参数空间R即可。
几何相具有拓扑变换不变性,正是我们千方百计要寻找的拓扑不变量。所谓的拓扑变换不变可作如下简要分析:An(R)依赖于波函数的规范。如果波函数取不同的规范,,则贝利连接必定改变,改变量 δAn(R)=−∇Rζ(R)。一般来讲,贝利相也会跟着改变,有 δγn(R)=δAn⋅dR。但是,几何相是实验可观测量,理应是规范不变的。为了抵消规范变换对贝利连接的影响,特选择封闭演化路径“C”。封闭路径下,R(0)=R(T)。波函数在规范变化前后都必须满足单值、连续性,即,必然导致,即 δγn=ζ(R(0))−ζ(R(T))=Δγn(R)=2πm,m=0,1,…。换句话说,无论规范怎么变换,几何相的取值都不会变,永远是2π的整数倍,其中m=0代表拓扑平庸,m=1,…,代表拓扑非平庸,此谓变换不变。
以上分析意味着连续的规范变换不改变贝利相γn。但如果规范不连续,则会产生2πm的相位变化。换句话说,贝利相不依赖于规范,但其取值依赖于规范的类别。具体地,如果能找到一个规范,这个规范在整个参数空间都有良定义,那么这个体系就是拓扑平庸的,无论对这个规范做什么样的连续变换,体系都能维持拓扑非平庸状态,δγ=0。对于某些特殊体系,无论取什么样的规范,都不可能做到波函数un(R)单值、连续,这样的体系是拓扑非平庸的。这种情况下,需要对波函数的奇异点的邻域和邻域以外的参数空间取不同的规范,才能保证波函数单值、连续,这种不连续的规范使得δγ=2πm,对这种不连续规范做连续变换,贝利相不变。因此,贝利相可作为拓扑不变量,表征体系在特定分类(拓扑平庸或非平庸)下的规范不变性。
1.3 贝利曲率
贝利连接An(R)依赖于规范,不是物理可观测量。参考磁场和磁矢势的定义,可以引入对标磁场的贝利曲率Ω(R)。利用斯托克斯公式,封闭路径的环量积分可化作有限面积的通量积分:
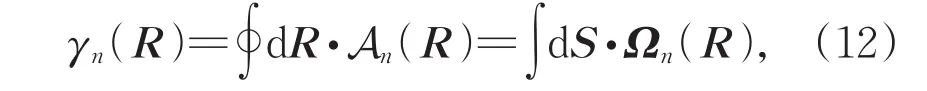


上式表明,贝利曲率Ω(R)在参数空间的每一点都不依赖于规范,等效于磁场,是可观测的局域变量。贝利相和贝利曲率都是规范不变的可观测量,但是贝利相只有在封闭路径下才有意义,贝利曲率则无此限制,故贝利曲率比贝利相更基础,也更重要。

1.4 单极点

由于体系哈密顿量空间各向同性,因此任何一个矢量方向R0都可以被指定作为自旋z方向。这意味着,方程(19)所表示的z分量就是事实上的R方向的分量由于贝利曲率守恒,对于二能级系统,只需一个能带的贝利曲率,选低能带,贝利曲率可写作

此贝利曲率是一个类似点电荷电场的辏力场,在场的源点R=0处,场函数发散,这样的贝利曲率是类似于电单极的单极点。根据贝利曲率写出贝利相
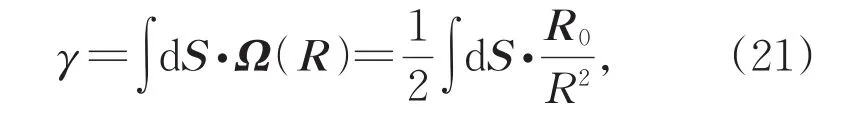
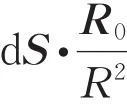
综上所述,通过定义在参数空间的规范无关的局域贝利曲率可以定义体系的贝利相,封闭曲面积分得到的贝利相直接反应体系的拓扑性。根据电场的高斯定律,封闭曲面可以不是球形,只要曲面封闭,形状可以任意。如果三维参数空间的封闭曲面内包含贝利曲率极点,则体系拓扑非平庸,如果不包含贝利曲率的极点,则拓扑平庸。这种对无规封闭曲面的通量积分,反应的正是立体方位角,也就是三维参数空间的自旋指向。只要自旋指向四面八方,则体系一定拓扑非平庸。在σz表象下,自旋指向四面八方意味着,自旋z可正可负。根据哈密顿量中自旋耦合形式σ⋅R,自旋z分量的正负取决于Rz,故Rz是体系拓扑性质的决定性因素。
需要说明的是,以上构建的各向同性的磁场和自旋耦合的哈密顿量是一个假想的、并不真的存在的理想玩具模型,构建此玩具模型旨在引入参数球和单极点,以便通过几何视角(球内还是球外)直观地表示拓扑序。尽管玩具模型所反映的参数球并不真的存在,我们依然可以通过参数映射,构建连续形变后的三维参数空间的封闭曲面。本文只关注二能级系统,所有二能级系统的参数空间都可以点点对应地映射到参数球R,这种映射不改变系统的拓扑性。因此,只要找出映射关系,以上关于体系拓扑性的分析可以直接用于所有二能级系统。
1.5 狄拉克方程

其中,矢量α和标量β均为归一化的狄拉克矩阵,α和β遵守Clifford代数的运算规则,满足反对易关系,据此定义高维参数空间,其参数分别代表动量项和质量项。为方便起见,用矢量α的维度定义狄拉克方程的维度。一维、二维体系,狄拉克矩阵可直接用泡利矩阵σ代替:αx=σx,αy=σy,β=σz。三维狄拉克矩阵为泡利矩阵的直积:

其中,i=x,y,z。
本文关注二维、三维体系的二能级模型,矢量α和标量β均为泡利矩阵,所有模型均可归为二维狄拉克方程。低能模型,用费米速度vF代替光速c,考虑到p=ℏk,质量项中的常数全部归入m,二维狄拉克费米子哈密顿量H=h(k)⋅σ 写作

这是我们熟知的AB子格势作用下的单层石墨烯的哈密顿量。如果把质量项稍作变形,m→mk=m0−k2,便得到二维拓扑绝缘体哈密顿量的一般形式,写作

以上所有狄拉克方程形式的哈密顿量均属于方程(18)所表示的二能级系统的一般形式。虽然哈密顿量(24)和(25)的参数空间是二维倒空间[kx,ky],无法形成1.4小节中的封闭曲面。然而,通过函数映射:k→R(k),可以把二维倒空间k映射到三维参数空间R。略掉无关紧要的常数,方程(24)和(25)均可通过参数映射定义新的三维参数空间 R=[kx,ky,m],其中对体系的拓扑性起关键作用的是质量项[参看1.4小节]。如果质量项m换成kz,便得到外尔半金属哈密顿量,写作倒空间的单极点H=ℏvF(k⋅σ),这意味着,外尔半金属必定拓扑非平庸。
基于二维狄拉克方程构架的方程(24)和(25)是两种典型的二能级系统,分别代表实空间的自然畴界型拓扑结构和通常意义下的体边对应的拓扑结构。所有的二能级系统都可以表示为参数k空间的狄拉克方程,通过参数映射k→R,可构建R空间的参数球,利用1.4小节介绍的特殊贝利相,可以方便地分析体系的拓扑性。下面我们分别以单层石墨烯、二维拓扑绝缘体、外尔半金属为例,分析体系拓扑性和参数空间R的深刻联系。核心思想有两个,第一,依托贝利相,结合狄拉克方程,分析几个典型的、已知的狄拉克费米子系统的拓扑性。第二,构建并预测新体系的拓扑性。
2 石墨烯拓扑态
石墨烯是二维平面上的三角复式晶格,每个原胞内有两个碳原子,对应两套子晶格,分别标记为A子格和B子格。单层石墨烯有AB两套子晶格,同时倒空间还有一对等效的狄拉克点,分别位于K、K′点,因此它具有多种二态内禀自由度。除了电子自旋,石墨烯还具有很多赝自旋,比如A/B子格、K/K′谷自旋,如果考虑多层石墨烯,外场对上下层的能量修正亦可构成赝自旋。这些因素为外部调控并修饰能带提供了非常丰富和便利的条件。不考虑元胞内的 势 能 分 布 V(r),H(k)=e−ik⋅rH(r)eik⋅r将 退 化为自旋σz表象下形如方程(22)的狄拉克费米子哈密顿量。并且,在加入各种外场和自旋轨道耦合后,单层、双层石墨烯经过适当的归一化变换后,都可以变为方程(22)。1.4小节已给出定论:参数空间的z分量Rz是体系拓扑性质的决定性因素。对于二维狄拉克费米子体系,Rz就是非零质量项。下面,将从狄拉克方程出发,分析几种典型的石墨烯模型,通过构造并调控狄拉克方程中的非零质量项,构建各种一维拓扑态,并简要研究一维拓扑态的输运性质。
2.1 AB子格势m
石墨烯置于氮化硼衬底上,AB子格感受到不同的范德瓦尔斯力的作用,在垂直电场作用下产生不同的感应势能,形成AB子格势,设UA−UB=m,即可引入狄拉克方程的质量项mσz。不考虑元胞内的势能分布V(r),略掉无关紧要的常数,H(k)退化为最简洁的二维狄拉克方程,写作
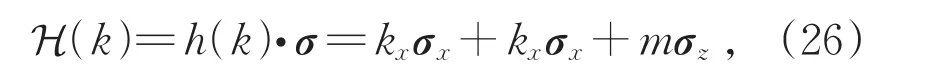
这是一个典型的自旋1/ 2的二能级系统。这里的自旋代表AB子格所张的希尔伯特空间的1/ 2赝自旋。固定m,哈密顿量的参数空间为二维体系的倒空间构成的二维平面,无论m取正还是取负,这样的参数空间都无法形成封闭曲面,自旋无法穿越参数空间的赤道面,自旋指向只能局限在上半球(m>0)或下半球(m<0),如图1(b)、(c)所示。因此,具有常数质量项的狄拉克费米子体系,必定拓扑平庸。

图1 单层石墨烯中由AB子格势构建的质量项。(a)质量项呈阶梯函数型,赝自旋指向四面八方;(b)质量项恒正,赝自旋z分量朝上;(c)质量项恒负,赝自旋z分量朝下Fig.1 Mass terms constructed byAB sublattice potential in monolayer graphene.(a)Mass term in staircase function form,pseudo-spin points to all directions;(b)Mass term remains positive with pseudo-spin's zcomponent all pointing up;(c)Mass term remains negative with pseudo-spin's z-component all pointing down
如何构建拓扑非平庸的边缘态呢?关键在质量项!哈密顿量(26)的参数空间R=[kx,ky,m],质量项 m 构成参数空间的第三个维度。如果质量项不是常数,而是随空间变化,比如设m=sgn(x)m,如图1(a)所示,则在三维参数空间任意取一个包围贝利曲率单极点R=0的封闭曲面,对贝利曲率作通量积分,都可得到非平庸的特殊贝利相γ=∮dS⋅Ω=2π。推而广之,只要质量项有明确的正负毗邻的边界,贝利曲率就一定会出现单极点,有几个单极点,便有几个拓扑态。质量为正的区域和质量为负的区域交替在实空间出现,类似于铁磁物质中的磁畴,正负质量毗邻的边界被称作畴壁或畴界,局域拓扑态只出现在畴界处。下面,通过定量化计算贝利相验证此结论。
利用贝利连接A和贝利曲率Ω求贝利相γ=∮dS⋅Ω=∮dS⋅∇A。所要积分的封闭曲面如图2所示,为无穷薄的柱体,柱体的表面为垂直于Rz的,向内和向外的两个Rx∧Ry平面。因此只需求贝利曲率的Rz分量,写作Ωkxky=的布洛赫本征模,
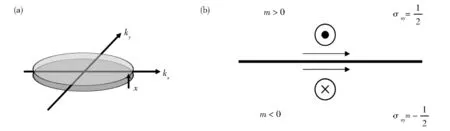
图2 实空间正负质量畴界形成的拓扑非平庸态。(a)函数映射后的参数空间的闭曲面;(b)手性相反毗邻而居的畴形成的拓扑畴界态Fig.2 Topological-nontrivial states formed by the domain boundary of positive and negative mass in real space.(a)Closed surface after mapping the function to a parameter space;(b)Topological domain boundary states formed by two adjacent domains with opposite chirality



理论上可以通过构建区域性的具有相反符号的质量畴[21],自由建设拓扑态的传播通道。图3展示了几种典型的拓扑通道,这种拓扑通道只允许能隙内的拓扑态通过,能够规避体态电子的杂质散射,大大降低体系的耗散性,通过畴界设计可以控制电子的传播方向,因此,这种畴界型拓扑态在电子电路方面有巨大的应用潜力[22-23]。

图3 通过畴界设计构造几种典型拓扑通道。其中,“+”表示手性为正的畴区,“-”表示手性为负的畴区Fig.3 Several typical topological channels built by designing the domain boundary,where "+" represents domain with positive chirality and "−" represents domain with negative chirality
下面用紧束缚模型[24-26]展示单层石墨烯体能隙中的拓扑畴界态最基本的体边对应关系。考虑最近邻耦合,实空间紧束缚哈密顿量
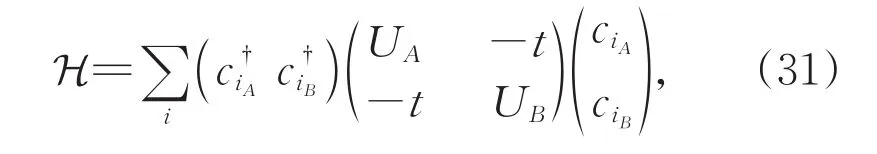
当AB子格势取常数,则质量项m为非零常数,非零质量项导致体能隙。进一步,考虑宽度有限的无穷长一维条带,条带有两个无穷长的锯齿形边界,上边界全部为A原子,下边界全部为B原子。沿两个锯齿形边界各有一条由不饱和C键贡献的,色散系数为零的平带,由于群速度为零,此平带对输运无贡献,如图4(a)所示。设总体质量项m为正数,即,所有A原子在位能为正值(实心圆),B子格为负值(空心圆),在此基础上,重置两个边界C原子的在位能。设上边界的A子格在位能=−1.0 t,下边界的B子格在位能=1.0 t,相当于在临近上下边界的实空间分别构建了一条分别由A子格和B子格贡献的正负交错的质量边界[27]。相应地,如图4(b)所示,原先分别由边界的A类碳原子和B类碳原子贡献的拓扑平庸的平带,现变为两个能谷处的拓扑非平庸的(质量)边界态。两能谷互为时间反演对称,故手性相反。由于,边界态的手性取决于质量项的符号,而A子格和B子格贡献质量项的在位能正好相反,故两个质量边界处的拓扑态手性也相反(参考图4(b)中的红色线和蓝色线)。如果y>0和y<0的区域AB势符号相反,则会形成如图4(c)中黑色短横线所示的正负质量界面,每个能谷处均有一个单极点,能带图中在两个能谷处自然会呈现手性相反的一对边缘态,文献中称之为零模态或kink态[28-31]。

图4 单层石墨烯条带的畴界拓扑能带(a)AB子格势,即质量项恒正,体系有体能隙但无边缘态或畴界态;(b)通过边缘修饰在两个边界处形成两个质量畴界,对应能带图能谷处的两条边缘态(红、蓝线);(c)AB子格势取阶梯函数,在中心位置构建正负质量畴界,对应能谷处的一条边缘态(黑色线)Fig.4 Domain boundary's topological band in monolayer graphene ribbon.(a)The system inAB sublattice potential where the mass term keeps positive only has body energy gap with no edge state or domain boundary state;(b)Edge modifying formed two mass domain boundaries along the two edge,corresponding to the two edge states(red and blue line)in the valley of the band picture;(c)AB sublattice potential is chosen to be staircase function form and its domain boundary of positive and negative mass is in the center,corresponding to an edge state(black line)in the valley
需要说明的是,AB子格势不破坏时间反演对称性,两类互为时间反演对称的狄拉克点附近的贝利曲率互为相反数,

因此,线性狄拉克费米子在K和K′点所能形成的拓扑态手性相反,可形成谷自旋霍尔态[32-35]。锯齿型边界的石墨烯条带具有K和K′点分离的特点,是观测谷自旋霍尔效应的首选材料。
2.2 AB堆垛双层石墨烯拓扑态
双层石墨烯中也存在类似的畴界拓扑态,而且物理更加丰富。两层单层石墨烯堆垛构成双层石墨烯,可以有不同的堆垛方式。两层原子完全重合的堆垛型称为AA堆垛。在此基础上,上下两层原子沿某一个最近邻方向相互位错一个最近邻的身位,使得某一层的A子格和另一层的B子格重叠,剩下的原子正对异层六角格子的正中心,如图5所示。

图5 双层石墨烯晶格结构:(a)AA堆叠;(b)AB堆叠Fig.5 Double-layer graphene's lattice structures(a)AA-stacking;(b)AB-stacking
和单层石墨烯一样,双层石墨烯的AB子晶格也可以构成子格赝自旋σ的希尔伯特空间,此外,上下两层层指标还可以构成层赝自旋τ的希尔伯特空间,整个哈密顿量写在σ×τ的4×4的希尔伯特空间,顶层(t)和底层(b)的AB原子构成哈密顿量基底,

在合适的垂直电场作用下,上下层在位能可以相反,设Ut−Ub=2Ut=u。AB堆垛的上下两层石墨烯彼此空间反演对称。综合考虑单层石墨烯层内耦合,上下两层层间耦合,及层内AB子格势,并设层内耦合强度为t1,层间耦合强度为t2,哈密顿量写作
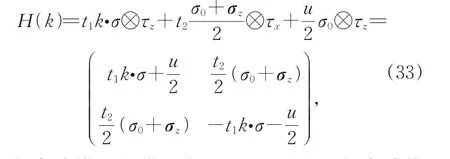
紧束缚模型能带图如图6(a)所示。紧束缚模型和低能有效模型有两点不同:(1)紧束缚模型不仅包含狄拉克点附近的低能线性区,也包含远离狄拉克点的非线性区;(2)两类不同的K点会同时出现在紧束缚模型倒空间,因此紧束缚能带有一条四重简并的、从K能谷到K′能谷的零能平带。在方程(32)的基础上,作归一化变换,用新基底

如果u=0,以上哈密顿量块对角,可看作两个相互独立无耦合的、具有等效于AB子格势的非零质量的、分别相对狄拉克点平移了±、消除了能量简并的“单层石墨烯”。两个单层石墨烯叠加,质量带隙消除,能带图如图6(b)所示,除了谷间平带,图6(b)的能带图和图6(a)的能带图完全相同①归一化变换仅适用于低能有效模型,低能线性区不包含谷间平带,图中已忽略谷间非零能平带。根据2.1小节的推断,常数型非零质量项[这里指σz项]必不能产生拓扑边界态,但是,如果u≠0,两个独立的狄拉克费米子互相耦合,带隙重新打开,形成反带隙,产生拓扑非平庸相变。AB堆叠层间耦合只对上层A原子和下层B原子作用,这导致四条平带中只有两条实现能级反转,最终形成体带隙中的边缘态[28,36]。每个能谷,每个物理边界都有一个边界态,如图6(c)所示。
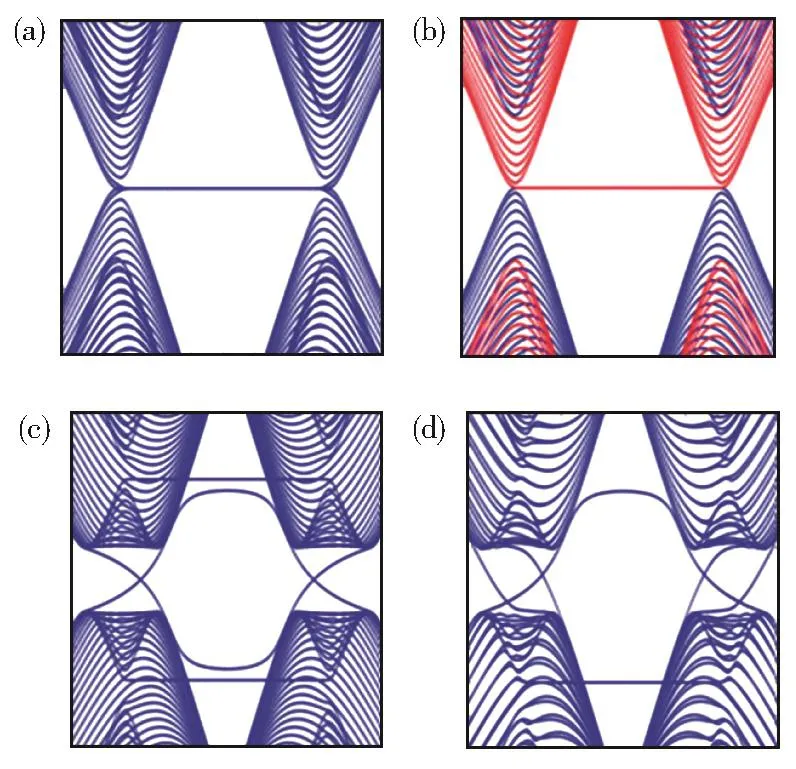
图6 具有锯齿型边界的双层石墨烯条带的能带(a-b)不考虑层间势(即U=0),(a)原始哈密顿量能带和(b)归一变换后的哈密顿量能带;(c-d)考虑层间势:(c)常数型层间势和(d)阶梯函数型层间势构成的异质结条带的能带Fig.6 Band of double-layer graphene ribbon with zig-zag edge.(a-b)Ignoring interlayer potential(U=0):(a)band of original Hamilton and(b)band of Hamilton after normalized transform;(c-d)Considering interlayer potential:Band of het‐erojunction ribbon under(c)constant interlayer potential and(d)staircase function form of interlayer potential
双层石墨烯哈密顿量是4能级哈密顿量,无法用前面所讲的参数映射方法通过理论分析判定它是否具有拓扑相,必须数值求解贝利曲率,数值结果表明−Ω(U)=Ω(−U)。层间势差U由堆叠方式决定,如果AB堆叠的层间势差为U,那么BA堆叠的层间势差就是−U。这意味着如果用AB堆叠型双层石墨烯和BA堆叠型双层石墨烯构建异质结,样品中将会有两块具有不同手性边缘态的物理区域,它们的分界线便是拓扑畴界,在拓扑畴界处会有两个边缘态[28],如图 6(d)所示。


图7 几种典型的畴界态和拓扑边缘态的分布情况。(a)单层石墨烯畴界拓扑态,由相邻畴区各贡献半个拓扑数;(b)双层石墨烯+常数型层间势形成的拓扑边缘态;(c)正负层间势畴区边缘态+手性相反的畴界形成的拓扑畴界态Fig.7 Distribution of several typical domain boundary states and topological edge states.(a)Monolayer graphene domain boundary states,two adjacent domains each devote half topological number;(b)Topological edge states formed by double-layer graphene with constant interlayer potential;(c)Edge states on the edge of positive and negative inter‐layer potential domain and topological domain boundary states formed by domain boundary with opposite chirality
2.3 次近邻耦合m(k)
在AB子格赝自旋的希尔伯特空间,AB子格相互作用贡献泡利矩阵的非对角项,也就是σx和σy结构参量的系数。AB子格内部互作用贡献泡利矩阵的对角项,也就是σz和σ0参量的系数,如果A子格内部作用和B子格内部作用相同,则此作用为σ0的系数,如果相反则为σz的系数,也就是狄拉克方程的质量项。AB子格势UA=−UB,贡献常数型质量项,如2.1小节所述,如果实空间存在正负质量界面,AB子格势便可以引起界面拓扑态。事实上,倒空间的正负质量界面也可以引起(真空)边界拓扑态,次近邻耦合刚好可以担任此角色。下面以Kane-Mele模型和更早的Haldane模型为例,说明次近邻耦合如何产生拓扑相变。
单层石墨烯,考虑最近邻耦合和Kane-Mele次近邻耦合,紧束缚模型哈密顿量写作:
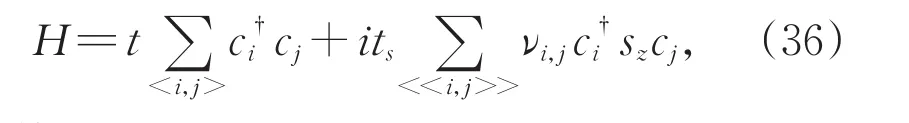
其中,第一项是发生在距离最近的不同子格间的最近邻相互作用,第二项是发生在距离最近的 同 类 子 格 之 间 的 次 近 邻 作 用 。是从同一个原子位置出发,分别终止于i和j的两个最近邻矢量的单位方向。由于A子格和B子格互为镜像,故A子格和B子格的次近邻作用符号相反,天然便是狄拉克方程中的非零质量项。紧束缚模型作傅里叶变换,可写出倒空间Kane-Mele模型的最近邻哈密顿量[17]



需要注意的是,Kane-Mele模型的次近邻耦合和Rashba自旋轨道耦合不同。Rashba自旋轨道耦合破坏结构对称性,是SU(2)型。而Kane-Mele自旋轨道耦合不破坏体系的结构对称性,是SU(1)型内禀自旋轨道耦合,并且它不破坏时间反演对称性,因此,sz=1的上自旋自旋轨道耦合和sz=−1的下自旋自旋轨道耦合互轭。此外,为保证镜面反射对称,A子格的自旋轨道耦合和B子格的自旋轨道耦合也要互轭。
综合最近邻和次近邻耦合,总的哈密顿量写作含质量项的狄拉克方程,H(k)=h(k)⋅σ,其中,h(k)=[tkx,tky,mKM(k)]。质量项 m(k)在倒空间正负交错,倒空间必有单极点,参看1.4小节。自旋上和自旋下的质量构型正好相反,二者对应的单极点的极性相反,拓扑边缘态的手性相反。一对具有不同自旋的手性相反的边缘态,构成时间反演对称保护的Z2拓扑绝缘体。
Haldane次近邻和Kane-Mele次近邻形式类似,描述的都是不同子格间互为共轭的次近邻耦合作用,但是二者的物理起源完全不同。Haldane模型是一个假想的玩具模型,Haldane次近邻类似于假想的赝磁场的作用效果,这个赝磁场对A子格和B子格的磁通刚好相反,可以理解为净磁通为零的周期赝磁场。赝磁场的磁矢势产生的磁通相位只出现在次近邻耦合项上,且A子格和B子格次近邻的磁通相位正好相反。设次近邻耦合强度为tn,Haldane模型次近邻哈密顿量写作[39-41]
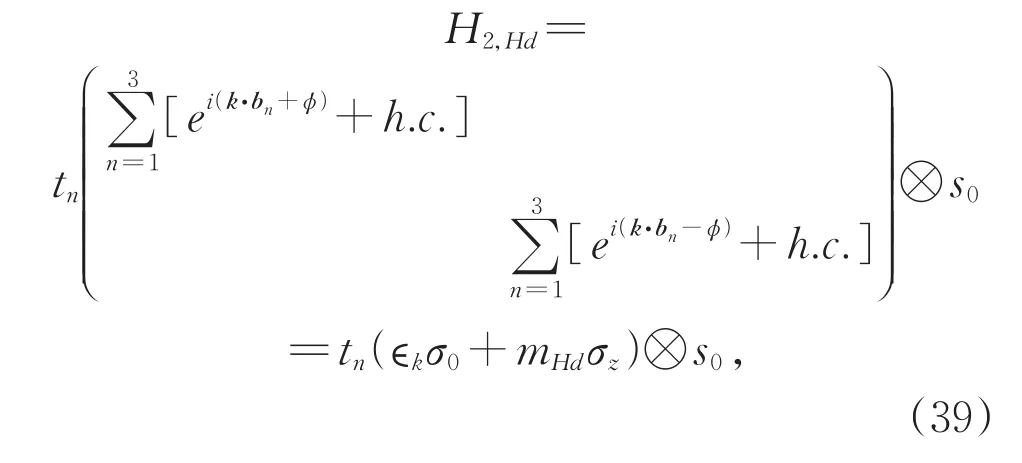

形式上,Haldane模型和Kane-Mele模型也有两点不同:(1)Kane-Mele模型中,对于不同的自旋,次近邻作用相反,H2,KM∝σzsz;而在 Haldane模型中,不同的自旋,其次近邻作用相同,H2,Hd∝σzs0。(2)Kane-Mele 模 型次近邻作用只包含质量项mKMσz;而在Haldane模型中,除了质量项 mHdσz,次近邻还可以包括常数项 ϵkσ0,但此常数项不影响体系的拓扑性,无需关注。非平庸能带如图8(a)所示,有明确的体带隙及拓扑边缘态。
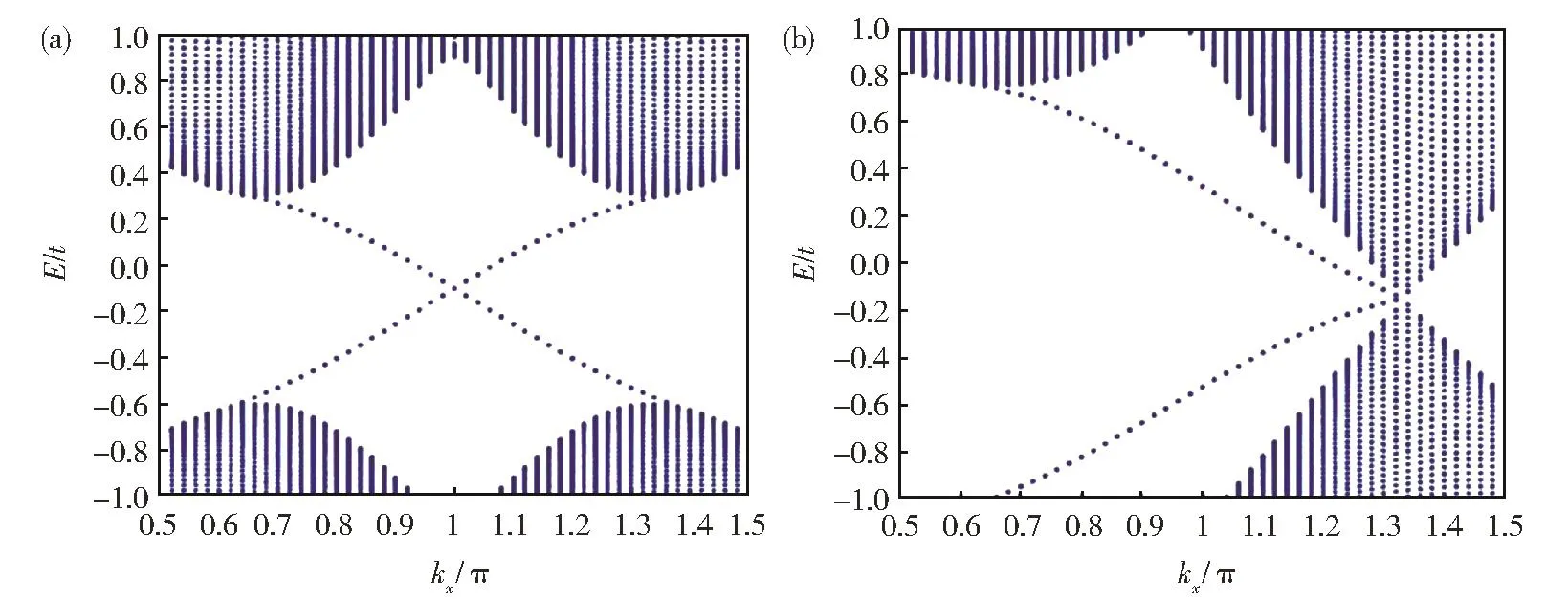
图8 单层石墨烯次近邻耦合能带图。(a)Haldane模型,不考虑AB子格势,体带隙最大,带隙内有鲁棒性边缘态;(b)AB子格势|M|=[2tnmax(|sinϕsin(k⋅bn)|)=3 tn|sinϕ|],带隙关闭,但鲁棒性边缘态仍存Fig.8 Band of monolayer graphene considering next-nearest coupling.(a)Haldane model,neglectingAB sublattice potential.The body gap is widest with robust edge states;(b)ConsideringAB sublat‐tice potential,the gap is closed but robust edge states still exists
在次近邻作用的基础上,再考虑AB子格势,设为UA=−UB=M,Haldane模型质量项写作

3 拓扑绝缘体
拓扑绝缘体是受时间反演对称保护的陈绝缘体。最简单的情况,自旋上和自旋下时间反演对称,且相互无耦合,相当于两个手性相反的陈绝缘体的合体。单看自旋上或自旋下的部分,和陈绝缘体无异,前面所有的推演全部适用。如果只考虑一种自旋,以HgTe/CdTe为代表的二维拓扑绝缘体,以及以(Bi,Sb)2Te3为代表的三维拓扑绝缘体,全部可以用狄拉克方程描写,

哈密顿量包含动量项和质量项。
3.1 二维拓扑绝缘体
以HgTe/CdTe为代表的二维拓扑绝缘体,哈密顿量表示为二维狄拉克方程形式,H(k)=ϵk+Ak⋅σ+Mkσz,矩阵形式如下[40,44-47]:
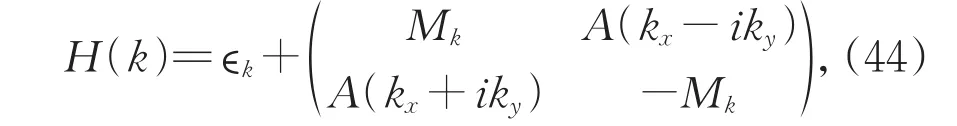
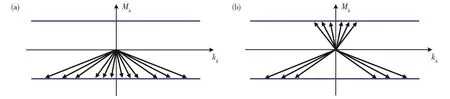
图9 二维拓扑绝缘在低能线性近似下的赝自旋分布。(a)M<0,质量项M−Bk2恒负;(b)M>0,质量项M−Bk2正负交错Fig.9 2-D topological insulator's spin distribution under low-energy linear approximation.(a)M<0,the mass termM−Bk2keeps negative;(b)M<0,the symbol of the mass termM−Bk2staggers
波矢k算符化,k→−i∇,用差分操作代替倒空间哈密顿量参数k,得到无穷长有限宽带边界的条带能带图 10。图 10(a)和图 10(b)分别展示了拓扑平庸和拓扑非平庸的能带结构,可以看出,不管是拓扑平庸还是拓扑非平庸,拓扑绝缘体的能带结构都存在体能隙,这也是它之所以被称作“绝缘体”的根本原因。二者的区别仅在于是否存在带隙内的拓扑边缘态。质量项恒正(或恒负)的拓扑平庸结构没有边缘态,是真正的绝缘体。质量项正负交错的拓扑非平庸结构具有非局域的边缘态,被称为拓扑绝缘体。拓扑绝缘体的带隙源于投影后的参数空间h(k)的特殊的第三维,也就是哈密顿量中的质量项。
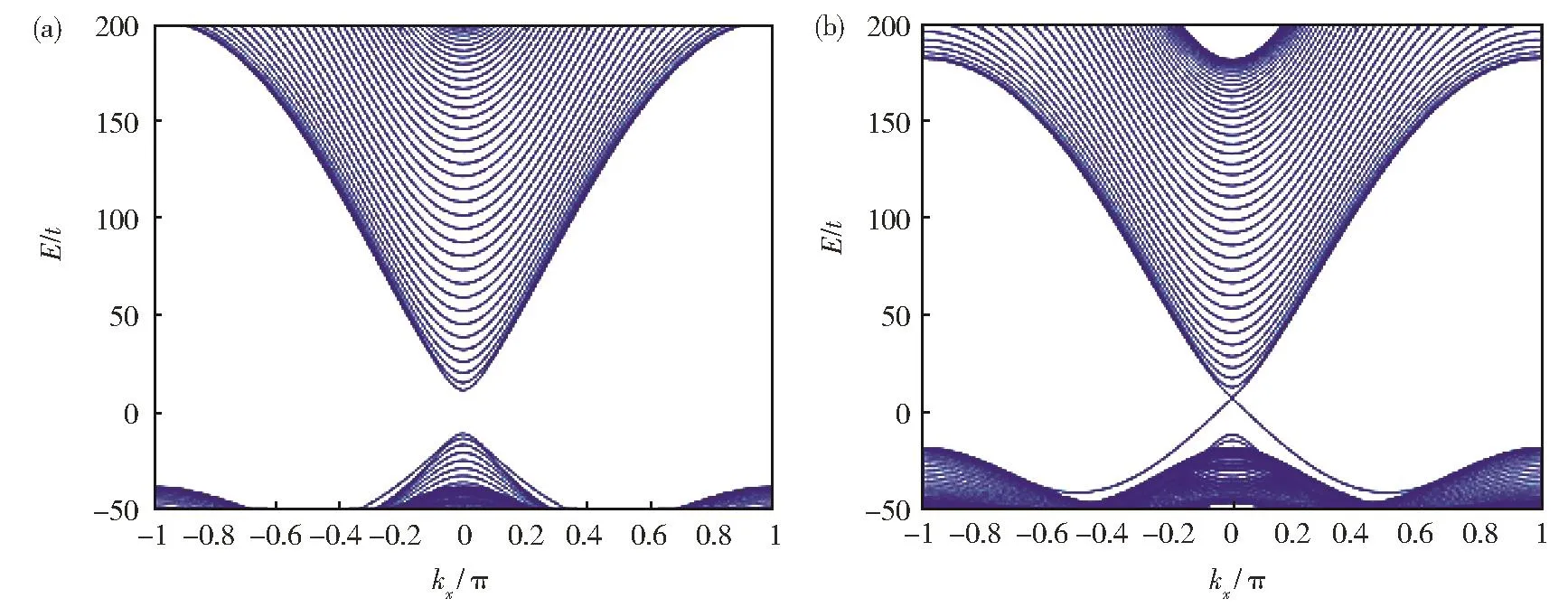
图10 二维拓扑绝缘体能带图。(a)M<0,拓扑平庸;(b)M>0,拓扑非平庸Fig.10 Band of 2-D topological insulator.(a)M<0,topological trivial;(b)M>0,topological nontrivial
综上,无论是石墨烯,还是拓扑绝缘体,所有用二维体系的线性狄拉克方程表示的体系,其拓扑性质都取决于质量项,一旦质量项正负交错,不管是在倒空间还是在实空间,体系必定拓扑非平庸,表现为具有鲁棒性的边缘态或畴界态。
3.2 三维拓扑绝缘体
如果把二维拓扑绝缘体进行简单堆叠,便可以构成三维拓扑绝缘体,但一般都是弱拓扑绝缘体[19]。如果沿x方向堆叠,那么只有(ky,kz)平面具有非零陈数,其他方向的陈数均为零。最直接的表现就是费米球不封闭,内含偶数个时间反演不动点,如图11(a)所示。以(Bi,Sb)2Te3为代表的三维强拓扑绝缘体则不同,从参数结构来看,它的三个方向结构相同,沿每一个方向构建的二维参数空间都能计算得到非零陈数。

图11 (a)弱拓扑绝缘体;(b)强拓扑绝缘体Fig.11 (a)Weak topological insulator;(b)Strong topological insulator
(Bi,Sb)2Te3系列材料的标志性哈密顿量结构如下[48-50]:


每一个块对角元都是一个二维拓扑绝缘体哈密顿量,体能隙内存在一维线性色散的边缘态。如果考虑kz分量,一维线性色散边缘态将演变为二维线性色散的狄拉克锥表面态。
综上,石墨烯和拓扑绝缘体在低能近似下都可以看作狄拉克费米子,但二者有几点不同:(1)石墨烯有一对等效狄拉克点,拓扑绝缘体只有一个;(2)石墨烯是二维狄拉克费米子,拓扑绝缘体不仅限于二维,理论上,一维、二维、三维均可。
3.3 量子反常霍尔效应
当三维拓扑绝缘体薄到极限,以至于上下表面的表面态可以直接耦合,形成两个相互耦合的狄拉克锥,以自旋上和自旋下的顶层表面态和底层表面态,,作为基底,哈密顿量进一步简化为[51]

塞曼场直接影响两个块对角的质量项,一个质量项增加另一个减少。当Δ>M时,其中一个块对角的质量项发生拓扑转变,从恒正变为正负交错,对应的块对角哈密顿量完全等效于方程(43),相当于只考虑一种自旋的二维拓扑绝缘体,体系进入量子反常霍尔相,拓扑陈数等于1,此拓扑陈数由上下表面共同贡献,如图12(a)所示。这种边缘态和石墨烯的质量畴界态类似,源于两个手性相反的毗邻而居的拓扑区域。已表明法向作为参考坐标,上下表面边缘态手性相反,侧表面相当于上下表面构成的相邻畴的畴界,如图12(b)所示。和石墨烯中通过AB子格势构建的拓扑畴界类似,参看2.1小节。侧表面彼此相距较远,不发生相互耦合,仍然保持线性色散关系。受面内塞曼场的影响,侧表面狄拉克锥发生平移,但依然维持零带隙的线性色散,上下表面态的边缘态可以在侧表面自由传播,如图12(c)所示。侧表面就是量子霍尔边缘态的实际传输通道,因此,侧表面的形貌将会深刻影响边缘态的品质[52-53]。
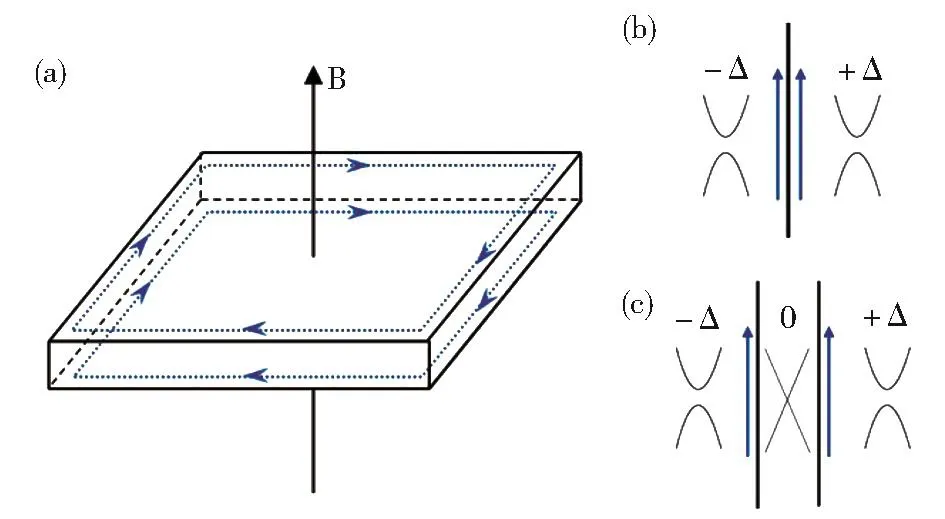
图12 (a)垂直塞曼场作用下的三维拓扑绝缘体薄层的手性边缘态;(b)半无穷薄层上下表面展开后构成的侧表面畴界态;(c)上下表面和侧表面态示意图,其中,侧表面无带隙,上下表面带隙内的边缘态可以在侧表面自由传播Fig.12 (a)Chiral edge states in 3-D topological insulator sheet under vertical Zeeman field;(b)Lateral surface domain boundary states formed by expanding half-infinite sheet's top and bottom surfaces;(c)Sketch of top,bottom and lateral surface states,where the lateral surface is gapless,edge states in top and bottom surface gap can freely transmit on lateral surface
4 外尔半金属
外尔半金属是表示在三维空间的二维狄拉克费米子[54-55],这里所谓的二维狄拉克费米子特指狄拉克方程的矢量参数α的维度(参考1.5小节)。由于体系受时间反演或空间反演对称保护,外尔半金属的能量节点必成对出现。如果体系同时具有时间反演对称性和空间反演对称性,体系将产生四重简并的外尔点,这种体系被称作狄拉克半金属,相当于两个外尔半金属的合体。石墨烯就是一种特殊的二维狄拉克半金属。外尔半金属和石墨烯有很多相同点:同属二能级系统,哈密顿量均可用二维狄拉克方程描述,并且二者的能量节点(狄拉克点或外尔点)均成对出现。但二者又有本质不同:首先,二者空间维度不同,石墨烯是二维系统的线性狄拉克费米子,外尔半金属是三维系统的线性狄拉克费米子,这将导致二者拓扑非平庸的表现也大不相同。
针对某一个外尔点k0,设有效动量q=k−k0,在外尔点附近针对有效动量作线性展开,得到外尔点附近的低能哈密顿量的一般形式[56]:

这是一个二能级哈密顿量,能级包含线性动能项和结构性各向同性的势能项。
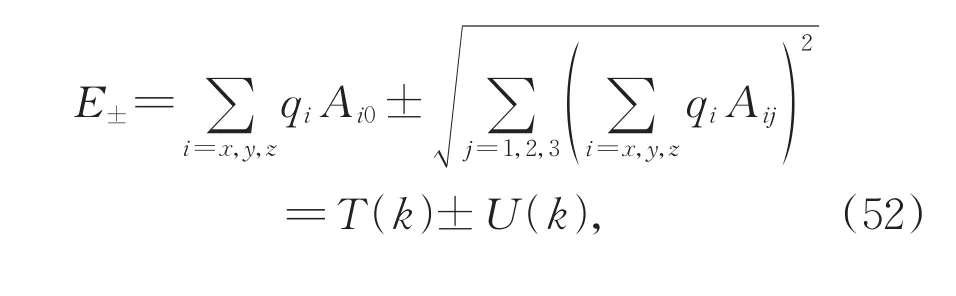
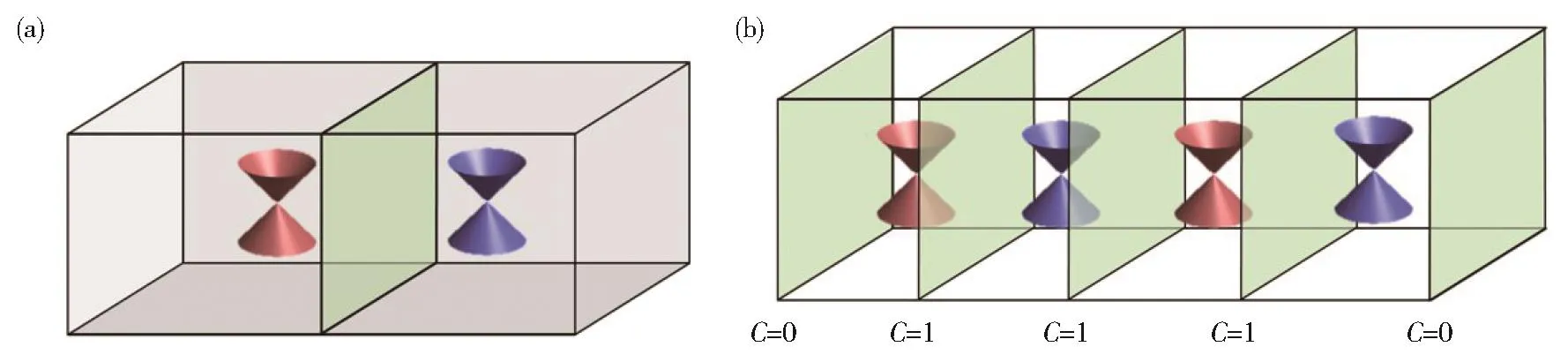
其中,线性动能项T(k)不改变二能级之差,但会改变各个方向的群速度,破坏洛伦兹对称性,使得原先各向同性的狄拉克锥发生倾斜,变成各向异性。如果T(k) 图13 (a)第一类普通型外尔半金属;(b)第二类外尔半金属Fig.13 (a)The first type as long as the common type of Weyl semi-metal;(b)The second type of Weyl semi-metal 下面以第一类外尔半金属为例,分析体系拓扑性。为简便计,直接略掉动能项。哈密顿量写作狄拉克方程的形式H(q)=h(q)⋅σ,其中,h(q)为动量空间的三维矢量,写作h(q)=[v1⋅q,v2⋅q,v3⋅q]。相当于沿 v̂1,v̂2,v̂3三个方向重新构建了新的动量参数空间。根据单极点理论,新参数空间的陈数可直接写出:C=sgn[v1⋅(v2×v3)]。如果三个方向和xyz坐标轴手性相同,贝利曲率闭积分为2π,对应陈数C=1,否则,如果二者手性相反,则陈数C=−1。这说明,外尔半金属天然便是拓扑非平庸的。 此外,由于外尔半金属的质量项同动量项一样,也是线性的,作为各项同性的单极点,外尔半金属不存在体带隙,这和前面讲过的石墨烯及拓扑绝缘体都不同,后两者均有体带隙。这表明三维空间的二维狄拉克方程和石墨烯以及二维拓扑绝缘体所代表的二维参数空间的二维狄拉克方程完全不同。后者需通过参数映射,用质量项构建映射后的参数空间的第三个维度,才能形成三维参数空间的单极点。外尔半金属哈密顿量原本就表示在三维参数空间,无需再通过质量项构建参数空间的第三维。 图14 外尔点及贝利曲率通量积分面。(a)倒空间能够完全分开两个外尔点的闭曲面,其贝利曲率通量贡献一个拓扑数;(b)两类平面:一类能够把外尔点完全分开,对应陈数C=1,另一类,不能分离两个外尔点,对应陈数C=0Fig.14 Weyl points and the integral surface of Berry curvature flux.(a)Closed surface in reciprocal space being able to fully separating two Weyl points,whose Berry curvature flux devotes to topologi‐cal number 1;(b)Two kind of surfaces:one can entirely separate the Weyl points,having Chern number 1 while the other can't,hav‐ing Chern number 0 至此,通过参数空间的单极点理论,我们成功地分析了石墨烯、拓扑绝缘体、外尔半金属的拓扑性。可以推测,所有能够用二维狄拉克方程描写哈密顿量的新材料,都可以通过参数空间的贝利曲率的单极点理论分析材料的拓扑性。外尔半金属和石墨烯、拓扑绝缘体都具有拓扑非平庸性,但他们的能带结构完全不同,前者没有体能隙,后者有带隙,这种能带结构的异同决定了它们的拓扑态的表现形式也必不相同。如前所述[2.1,2.3,3.1],石墨烯、拓扑绝缘体的拓扑态存在体能隙,因此,可以很好地定义具有明确的体边对应关系的边界态或表面态。外尔半金属无能隙,并不存在真正意义上的表面态,因为不同的表面态之间总是可以通过外尔点实现互通。即便如此,我们依然可以定义表面上的投影态。 一般来说,固定能量的费米面在倒空间表现为封闭曲面,投影到某个方向的表面,其二维倒空间的费米面将变为封闭曲线,如图15(a)所示,这是普通的体态投影。如果费米面刚好穿过一对外尔点,体态对应的费米面从两个球面退化为倒空间一对孤立点,即外尔点。除了体态费米面,外尔半金属在外尔点之外的体带隙内还存在拓扑表面态,投影到样品表面,成为连接两个外尔点的费米弧。如图15(b)所示,二维表面的倒空间的投影态上,所有的点都是真正的表面态,除了两个外尔点。两个外尔点所代表的态函数是体态,可以深入体内,同时在表面也有投影态。一对外尔点手性相反,相当于贝利流的源和漏,随着动量波矢参数演化,所有可能的态,包括体带隙内的表面投影态,必始于源终于漏,所有可能的表面态连成表面倒空间连接两个外尔点的费米弧。考虑到体系的空间反演对称性,固定[qx,qy]≠0的表面态总是成对出现,分别位于z方向的上表面和下表面,因此,每一个表面都有一条连接外尔点的费米弧。当费米面偏离外尔点,体态范围扩大,呈闭曲面,其表面投影态由两个孤立外尔点扩展为两条封闭曲线,即联通表面态的源和漏由外尔点变为封闭曲线,与此同时,体带隙范围缩小,但连接两片单连通区域的费米弧仍存在,甚至当源和漏的范围继续扩大以至于局域相互融合,连接源和漏的费米弧也依然存在,如图 15(c)、(d)所示。费米弧连接源和漏,是无能隙的外尔半金属的拓扑指征[57],不同类型的费米弧可作为表征不同外尔半金属材料的指纹。 图15 在二维倒空间表示的实空间的表面投影态。(a)普通费米球的表面投影态,拓扑平庸,无费米弧;(b-d)外尔半金属的表面投影态,拓扑非平庸,有费米弧。(b)费米面在外尔点;(c)费米面偏离外尔点;(d)费米面严重偏离外尔点,以至于两个外尔点的体态部分融合Fig.15 Surface projected states of real space expressed in 2-D reciprocal space.(a)Normal Fermi sphere's surface projected state,topological trivial,no Fermi arc;(b-d)Weyl semi-metal's surface projected state,topological nontrivial,with Fermi arc;(b)Weyl points are right on the Fermi surface;(c)Fermi surface deviate from Weyl points;(d)Fermi surface severely deviate from Weyl points so that the two Weyl points'body states are partly fused 二能级系统看似简单,却包含了丰富的物理。大多数凝聚态拓扑材料最核心的物理都可以归结为简单的二能级模型。所有二能级模型都可以表示成二维狄拉克方程的形式,通过参数映射,可以把所有的二能级系统等效为倒空间的单极点。通过判断单极点的方位,无需计算贝利曲率,只要单极点位于封闭参数空间内部,便可直接判定体系的拓扑非平庸性。 我们选取三类典型材料:石墨烯、拓扑绝缘体、外尔半金属,展示如何通过参数映射后的单极点模型,直接判断体系的拓扑性。结果显示,对于二维体系,比如石墨烯和拓扑绝缘体,二能级系统拓扑非平庸的关键在于质量项,只要质量项正负交错,便可以在正负两个方向上构成参数空间至关重要的第三维,从而形成包含单极点的封闭曲面,这样的体系一定拓扑非平庸。质量项正负交错可以发生在正空间,比如石墨烯的AB势构成的质量畴界,也可以发生在倒空间,比如石墨烯的次近邻作用、拓扑绝缘体的非平庸质量项。对于三维体系,比如外尔半金属,三个方向均满足线性色散,质量项一定是正负交错的,因此,外尔半金属天生便是拓扑非平庸材料。 石墨烯和拓扑绝缘体可归结为二维参数空间的二维狄拉克方程,外尔半金属则归为三维参数空间的二维狄拉克方程。尽管同属拓扑非平庸材料,但外尔半金属和石墨烯、二维拓扑绝缘体的表现大不相同。二维参数空间的二维狄拉克方程的拓扑非平庸态有明确的体边对应的边界态,这种边界态可以是毗邻而居的、具有不同手性的畴域构成的毗邻畴界态,或者是居于物理边界的边界态。与此形成鲜明对比的是三维参数空间的二维狄拉克方程,它的拓扑非平庸态不是边界态,而是二维表面的费米弧。 通过参数映射后的单极点模型,可以方便快捷地判断新材料的拓扑性质。不仅如此,还可以借鉴点电荷场分布,通过场通量快速计算贝利相。单极点模型简单、易行、方便、快捷,是研究二能级系统不可或缺的利器。充分利用单极点模型可以删繁就简,有助于深刻理解二能级系统的拓扑性。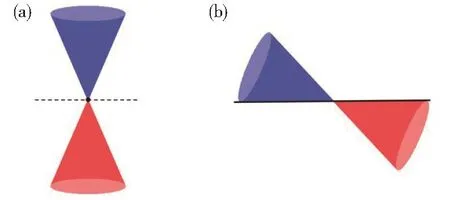
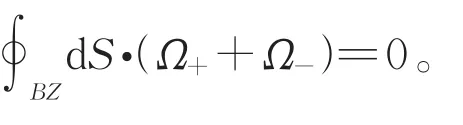

5 结论

